Ich bin auf ein interessantes Rätsel gestoßen: In der Tat sind die Zahl a und die positive ganze Zahl n angegeben. Berechnen Sie die n-te Wurzel einer Zahl ohne Verwendung von Bibliotheken.
Eingabedaten: Die Zahl a ist real, nicht negativ, überschreitet 1000 nicht und wird mit einer Genauigkeit von 6 Dezimalstellen angegeben. Die Zahl n ist natürlich und überschreitet 10 nicht.
Ausgabe: Das Programm sollte eine einzelne Zahl ausgeben: die Antwort auf das Problem mit einer Genauigkeit von mindestens 5 Dezimalstellen.
Natürlich war es interessant, es in einem Entwurf mit einem Bleistift zu lösen, es dann im Editor zu zeichnen und zu kompilieren. Ohne zu googeln, Tipps und vor allem mit Bibliotheken. Wenn Sie dies zum ersten Mal entscheiden, versuchen Sie zunächst, ein Programm zu schreiben, um die übliche Quadratwurzel zu finden. Wenn Sie die Aufgabe schwierig finden, lösen Sie sie fast gleich, aber einfacher. Dann wird deine Angst verschwinden und es wird eine Art grobes Verständnis entstehen.
Für den Anfang werde ich ein Beispiel geben, wie die Quadratwurzel ohne Verwendung einer Bibliotheksfunktion berechnet wird. Sequentieller Iterationsalgorithmus. Es konvergiert auch bei großen Zahlen recht schnell.
#include <stdio.h> int main(void) { double num = 570.15; double root = num / 2; double eps = 0.01; int iter = 0; while( root - num / root > eps ){ iter++; root = 0.5 * (root + num / root); printf("Iteration: %d : root = %f\n", iter, root); } printf("root = %f", root); return 0; }
Sie können den Code hier
ausführen :
KLICKENDie logarithmische Komplexität des Algorithmus? Oder eine andere? :) :)
Jetzt können Sie mit der komplizierten Version der Aufgabe fortfahren. In diesem Fall ist die Lösung allgemeiner.
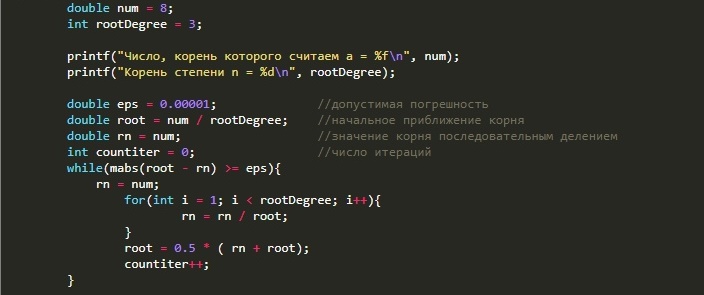
#include <stdio.h> double mabs(double x){ return (x < 0)? -x : x; } int main(void) { double num = 8; int rootDegree = 3; printf(", = %f\n", num); printf(" n = %d\n", rootDegree); double eps = 0.00001; // double root = num / rootDegree; // double rn = num; // int countiter = 0; // while(mabs(root - rn) >= eps){ rn = num; for(int i = 1; i < rootDegree; i++){ rn = rn / root; } root = 0.5 * ( rn + root); countiter++; } printf("root = %f\n", root); printf(" = %i\n", countiter); return 0; }
Sie können den Code hier
ausführen :
KLICKENIn dieser Lösung verwende ich die Idee einer relativ guten anfänglichen Annäherung. Dann ist die sequentielle Division die zweite Annäherung an die Wurzel des n-ten Grades. Als nächstes wird eine neue Näherung betrachtet, indem die beiden aktuellen gemittelt werden. Konsistent konvergiert der Algorithmus mit einem vorbestimmten Fehler zur gewünschten Wurzel. Dies ist ein bisschen wie eine einfache Iterationsmethode.
Dies ist der erste Arbeitsalgorithmus, der auf das Knie geschrieben wurde. Wir müssen noch über die Komplexität und die Möglichkeiten der Beschleunigung nachdenken. Welche Beschleunigungsmerkmale dieses Algorithmus können Ihrer Meinung nach übrigens implementiert werden?
Ich habe das Gefühl, dass es eine Frage geben wird: "Warum das tun, wenn alles vor hundert Jahren in Bibliotheken implementiert wurde ?!"
Antwort: Ich persönlich habe immer gerne über Algorithmen nachgedacht, die bereits in Standardbibliotheken implementiert sind. Versuchen Sie, sie selbst zu entwickeln (na ja, oder eine Art langsame Parodie zu entwickeln und zu scheitern). Es trainiert das Gehirn sehr gut. Daher ist es meiner Meinung nach sehr nützlich, das Rad neu zu erfinden. Und es ist kategorisch schädlich, immer alles bereit zu haben, ohne eine Vorstellung von der internen Struktur zu haben.