Es wurde viel über numerische Optimierungsmethoden geschrieben. Dies ist verständlich, insbesondere vor dem Hintergrund der Erfolge, die kürzlich durch tiefe neuronale Netze gezeigt wurden. Und es ist sehr erfreulich, dass zumindest einige Enthusiasten nicht nur daran interessiert sind, wie sie ihr neuronales Netzwerk auf die Frameworks bombardieren können, die in diesem Internet an Popularität gewonnen haben, sondern auch, wie und warum alles funktioniert. In letzter Zeit musste ich jedoch feststellen, dass bei der Beantwortung von Fragen zum Training neuronaler Netze (und nicht nur zum Training und nicht nur zu Netzen), einschließlich Habré, immer häufiger eine Reihe von „bekannten“ Aussagen für die Weiterleitung verwendet werden, deren Gültigkeit gelinde gesagt zweifelhaft. Unter solchen zweifelhaften Aussagen:
- Methoden der zweiten und weiteren Ordnung funktionieren beim Training neuronaler Netze nicht gut. Weil.
- Die Newton-Methode erfordert eine positive Bestimmtheit der hessischen Matrix (zweite Ableitungen) und funktioniert daher nicht gut.
- Die Levenberg-Marquardt-Methode ist ein Kompromiss zwischen Gradientenabstieg und Newton-Methode und allgemein heuristisch.
usw. Um diese Liste fortzusetzen, ist es besser, zur Sache zu kommen. In diesem Beitrag werden wir die zweite Aussage betrachten, da ich ihn in Habré nur mindestens zweimal getroffen habe. Ich werde auf die erste Frage nur in dem Teil eingehen, der die Newton-Methode betrifft, da sie viel umfangreicher ist. Der dritte und der Rest bleiben bis zu besseren Zeiten.
Im Mittelpunkt unserer Aufmerksamkeit steht die Aufgabe der bedingungslosen Optimierung
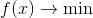
wo
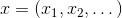
- ein Punkt des Vektorraums oder einfach - ein Vektor. Natürlich ist diese Aufgabe umso einfacher zu lösen, je mehr wir darüber wissen

. Es wird normalerweise angenommen, dass es in Bezug auf jedes Argument differenzierbar ist
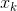
und so oft wie nötig für unsere schmutzigen Taten. Es ist bekannt, dass eine notwendige Bedingung dafür an einem Punkt ist
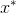
Das Minimum ist erreicht, ist die Gleichheit des Gradienten der Funktion
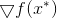
an diesem Punkt Null. Von hier erhalten wir sofort die folgende Minimierungsmethode:
Löse die Gleichung
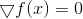
.
Die Aufgabe ist, gelinde gesagt, nicht einfach. Auf keinen Fall einfacher als das Original. An dieser Stelle können wir jedoch sofort den Zusammenhang zwischen dem Minimierungsproblem und dem Problem der Lösung eines Systems nichtlinearer Gleichungen feststellen. Diese Verbindung wird bei der Betrachtung der Levenberg-Marquardt-Methode (wenn wir dazu kommen) auf uns zurückkommen. Denken Sie in der Zwischenzeit daran (oder finden Sie heraus), dass eine der am häufigsten verwendeten Methoden zum Lösen von Systemen nichtlinearer Gleichungen die Newtonsche Methode ist. Es besteht in der Tatsache, dass die Gleichung zu lösen

Wir gehen von einer anfänglichen Annäherung aus

Erstellen Sie eine Sequenz
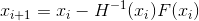
- Newtons explizite Methode
oder
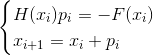
- Newtons implizite Methode
wo

- Matrix aus partiellen Ableitungen einer Funktion

. Im allgemeinen Fall, wenn uns das System der nichtlinearen Gleichungen einfach in Empfindungen gegeben wird, ist natürlich etwas von der Matrix erforderlich

wir sind nicht berechtigt. In dem Fall, in dem die Gleichung eine Mindestbedingung für eine Funktion ist, können wir angeben, dass die Matrix

symmetrisch. Aber nicht mehr.
Newtons Methode zur Lösung nichtlinearer Gleichungssysteme wurde recht gut untersucht. Und hier ist die Sache - für ihre Konvergenz ist die positive Bestimmtheit der Matrix nicht erforderlich

. Ja, und kann nicht verlangt werden - sonst wäre er wertlos gewesen. Stattdessen gibt es andere Bedingungen, die eine lokale Konvergenz dieser Methode gewährleisten und die wir hier nicht berücksichtigen werden, indem wir interessierte Personen zur Fachliteratur (oder in den Kommentaren) schicken. Wir bekommen die Aussage 2 ist falsch.
Also?
Ja und nein. Der Hinterhalt hier im Wort ist die lokale Konvergenz vor dem Wort. Dies bedeutet, dass die anfängliche Annäherung

muss „nah genug“ an der Lösung sein, sonst werden wir bei jedem Schritt immer weiter von ihr entfernt. Was tun? Ich werde nicht näher darauf eingehen, wie dieses Problem für Systeme nichtlinearer Gleichungen allgemeiner Form gelöst wird. Zurück zu unserer Optimierungsaufgabe. Der erste Fehler von Aussage 2 ist tatsächlich, dass die Newton-Methode bei Optimierungsproblemen normalerweise ihre Modifikation bedeutet - die gedämpfte Newton-Methode, bei der die Folge von Approximationen gemäß der Regel konstruiert wird
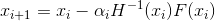
- Newtons explizite gedämpfte Methode
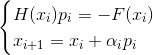
- Newtons implizite gedämpfte Methode
Hier ist die Reihenfolge
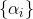
ist ein Parameter der Methode und ihre Konstruktion ist eine separate Aufgabe. Bei Minimierungsproblemen natürlich bei der Auswahl
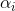
es wird eine Anforderung bestehen, dass bei jeder Iteration der Wert der Funktion f abnimmt, d.h.
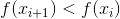
. Es stellt sich eine logische Frage: Gibt es eine solche (positive)
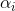
? Und wenn die Antwort auf diese Frage positiv ist, dann

nannte die Richtung des Abstiegs. Dann kann die Frage folgendermaßen gestellt werden:
Wann ist die nach Newtons Methode erzeugte Richtung die Abstiegsrichtung?Und um es zu beantworten, müssen Sie das Minimierungsproblem von einer anderen Seite betrachten.
Abstiegsmethoden
Für das Minimierungsproblem erscheint dieser Ansatz ganz natürlich: Ausgehend von einem beliebigen Punkt wählen wir die Richtung p auf irgendeine Weise und machen einen Schritt in diese Richtung
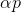
. Wenn
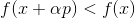
dann nimm
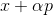
als neuen Ausgangspunkt und wiederholen Sie den Vorgang. Wenn die Richtung willkürlich gewählt wird, wird eine solche Methode manchmal als Random-Walk-Methode bezeichnet. Es ist möglich, Einheitsbasisvektoren als Richtung zu verwenden - das heißt, um einen Schritt in nur einer Koordinate zu machen, wird diese Methode als Koordinatenabstiegsmethode bezeichnet. Unnötig zu sagen, dass sie unwirksam sind? Damit dieser Ansatz gut funktioniert, benötigen wir einige zusätzliche Garantien. Dazu führen wir eine Hilfsfunktion ein
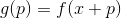
. Ich denke, es ist offensichtlich, dass die Minimierung

völlig gleichbedeutend mit Minimierung

. Wenn

dann differenzierbar

kann dargestellt werden als
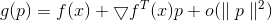
und wenn
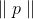
klein genug dann
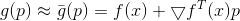
. Wir können jetzt versuchen, das Minimierungsproblem zu ersetzen
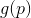
die Aufgabe der Minimierung seiner Annäherung (oder
Modell )
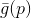
. Übrigens basieren alle Methoden auf der Verwendung des Modells
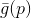
Gradient genannt. Aber das Problem ist,
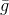
Ist eine lineare Funktion und hat daher kein Minimum. Um dieses Problem zu lösen, fügen wir eine Einschränkung für die Länge des Schritts hinzu, den wir ausführen möchten. In diesem Fall ist dies eine ganz natürliche Voraussetzung - denn unser Modell beschreibt die Zielfunktion nur in einer ausreichend kleinen Nachbarschaft mehr oder weniger korrekt. Als Ergebnis erhalten wir ein zusätzliches Problem der bedingten Optimierung:
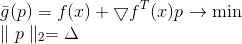
Diese Aufgabe hat eine offensichtliche Lösung:
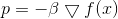
wo

- Faktor, der die Erfüllung der Bedingung garantiert. Dann nehmen Iterationen der Abstiegsmethode die Form an
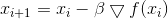
,
in dem wir die bekannte
Gradientenabstiegsmethode lernen. Parameter

, die üblicherweise als Abstiegsgeschwindigkeit bezeichnet wird, hat nun eine vollständig verständliche Bedeutung erhalten, und ihr Wert wird aus der Bedingung bestimmt, dass der neue Punkt auf einer Kugel mit einem bestimmten Radius liegt, die um den alten Punkt herum umschrieben ist.
Basierend auf den Eigenschaften des konstruierten Modells der Zielfunktion können wir argumentieren, dass es solche gibt

, auch wenn sehr klein, was wäre wenn
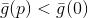
dann

. Es ist bemerkenswert, dass in diesem Fall die Richtung, in die wir uns bewegen, nicht von der Größe des Radius dieser Kugel abhängt. Dann können wir einen der folgenden Wege wählen:
- Wählen Sie nach einer Methode den Wert aus
 .
. - Stellen Sie die Aufgabe ein, den entsprechenden Wert auszuwählen
 , was eine Abnahme des Wertes der Zielfunktion bewirkt.
, was eine Abnahme des Wertes der Zielfunktion bewirkt.
Der erste Ansatz ist typisch für die
Methoden der Vertrauensregion , der zweite führt zur Formulierung des Hilfsproblems der sogenannten
lineare Suche (LineSearch) . In diesem speziellen Fall sind die Unterschiede zwischen diesen Ansätzen gering und werden nicht berücksichtigt. Beachten Sie stattdessen Folgendes:
Warum suchen wir eigentlich nach einem Offset?  genau auf der Kugel liegen?
genau auf der Kugel liegen?Tatsächlich könnten wir diese Einschränkung gut durch die Anforderung ersetzen, dass beispielsweise p zur Oberfläche des Würfels gehört, d. H.
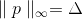
(in diesem Fall ist es nicht zu vernünftig, aber warum nicht) oder eine elliptische Oberfläche? Dies erscheint bereits ziemlich logisch, wenn wir uns an die Probleme erinnern, die bei der Minimierung von Gully-Funktionen auftreten. Das Wesentliche des Problems ist, dass sich die Funktion entlang einiger Koordinatenlinien viel schneller ändert als entlang anderer. Aus diesem Grund erhalten wir, dass, wenn das Inkrement zur Kugel gehören sollte, die Menge

bei dem der "Abstieg" vorgesehen ist, sollte sehr klein sein. Und dies führt dazu, dass das Erreichen eines Minimums eine sehr große Anzahl von Schritten erfordert. Aber wenn wir stattdessen eine geeignete Ellipse als Nachbarschaft nehmen, wird dieses Problem auf magische Weise zunichte gemacht.
Durch die Bedingung, dass die Punkte der elliptischen Oberfläche gehören, kann es geschrieben werden als
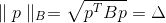
wo

Ist eine positive bestimmte Matrix, auch Metrik genannt. Norm
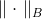
genannt die durch die Matrix induzierte elliptische Norm

. Was für eine Matrix ist das und woher kann man sie beziehen? Wir werden später darüber nachdenken, und jetzt kommen wir zu einer neuen Aufgabe.
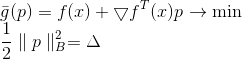
Das Quadrat der Norm und der 1/2 Faktor dienen hier nur der Einfachheit halber, um nicht mit den Wurzeln herumzuspielen. Mit der Lagrange-Multiplikatormethode erhalten wir das gebundene Problem der bedingungslosen Optimierung
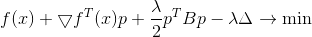
Eine notwendige Bedingung für ein Minimum dafür ist
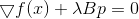
oder
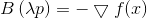
von wo
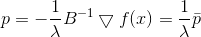
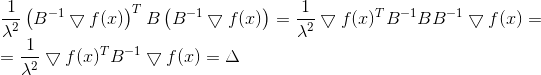
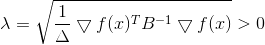
Wieder sehen wir, dass die Richtung
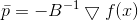
, in dem wir uns bewegen werden, hängt nicht vom Wert ab

- nur aus der Matrix

. Und wieder können wir entweder abholen

das ist mit der Notwendigkeit der Berechnung behaftet

und explizite Matrixinversion

oder lösen Sie das Hilfsproblem, eine geeignete Vorspannung zu finden
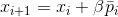
. Seit
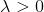
ist die Lösung für dieses Hilfsproblem garantiert.
Was soll es also für Matrix B sein? Wir beschränken uns auf spekulative Ideen. Wenn das Ziel funktioniert

- quadratisch, das heißt, es hat die Form
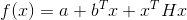
wo

positiv definitiv ist es offensichtlich, dass der beste Kandidat für die Rolle der Matrix

ist hessisch

, da in diesem Fall eine Iteration der von uns konstruierten Abstiegsmethode erforderlich ist. Wenn H nicht eindeutig positiv ist, kann es keine Metrik sein, und die damit konstruierten Iterationen sind Iterationen der gedämpften Newton-Methode, aber keine Iterationen der Abstiegsmethode. Schließlich können wir eine strenge Antwort geben
Frage: Muss die hessische Matrix in der Newton-Methode positiv eindeutig sein?Antwort: Nein, es ist weder in der Standard- noch in der gedämpften Newton-Methode erforderlich. Wenn diese Bedingung erfüllt ist, ist die gedämpfte Newton-Methode eine Abstiegsmethode und hat die Eigenschaft der globalen und nicht nur der lokalen Konvergenz.Lassen Sie uns zur Veranschaulichung sehen, wie Vertrauensbereiche aussehen, wenn die bekannte Rosenbrock-Funktion mithilfe von Gradientenabstieg und Newtons Methoden minimiert wird, und wie sich die Form der Bereiche auf die Konvergenz des Prozesses auswirkt.
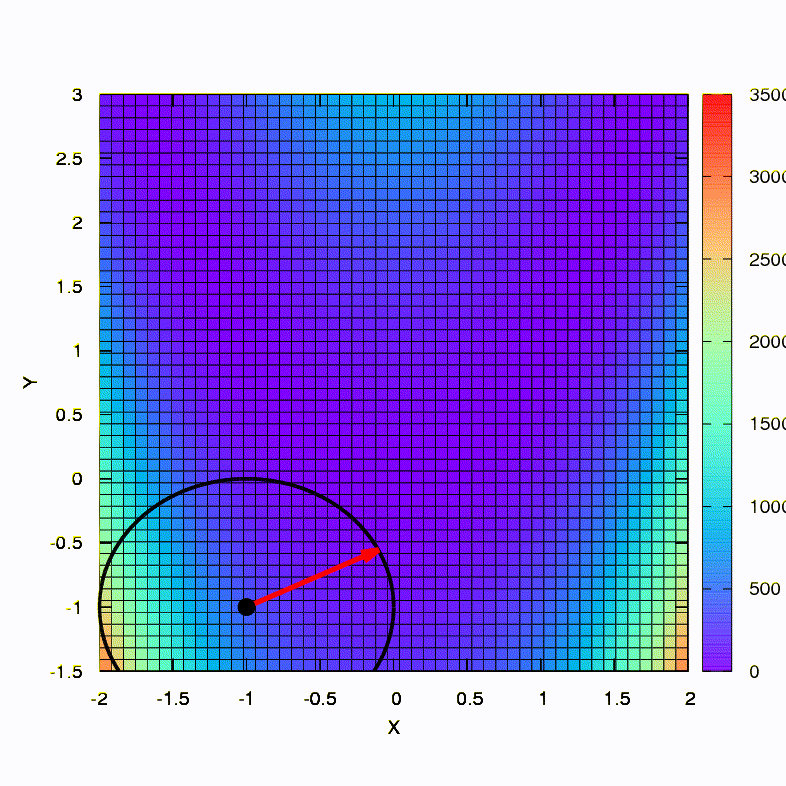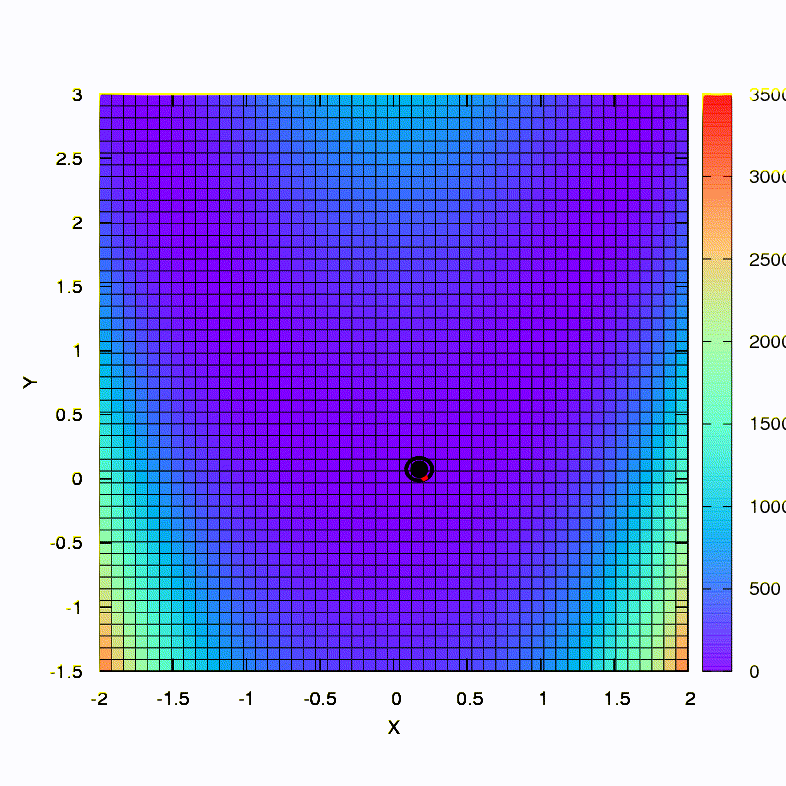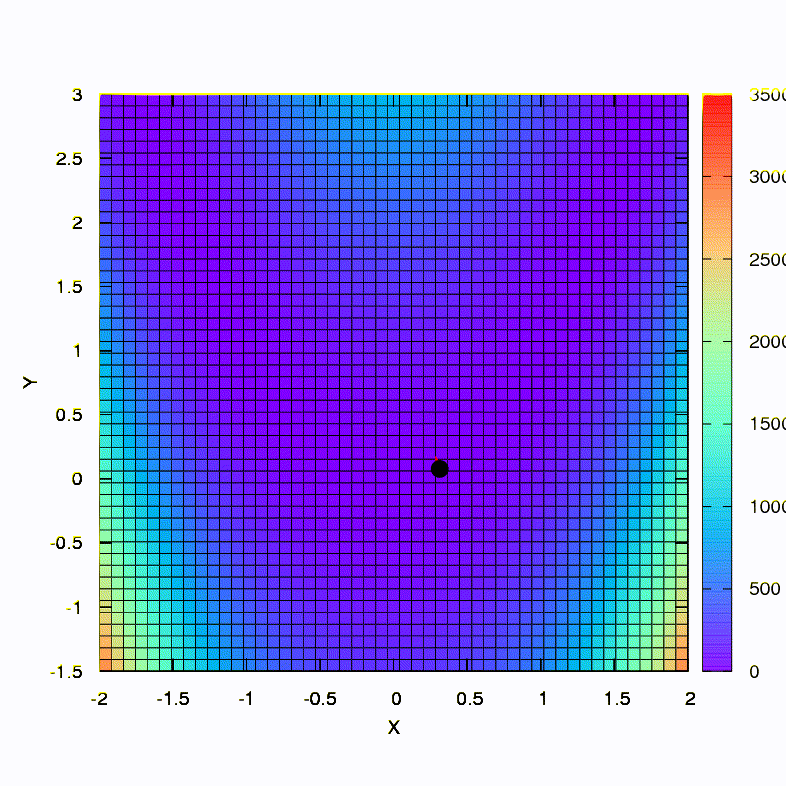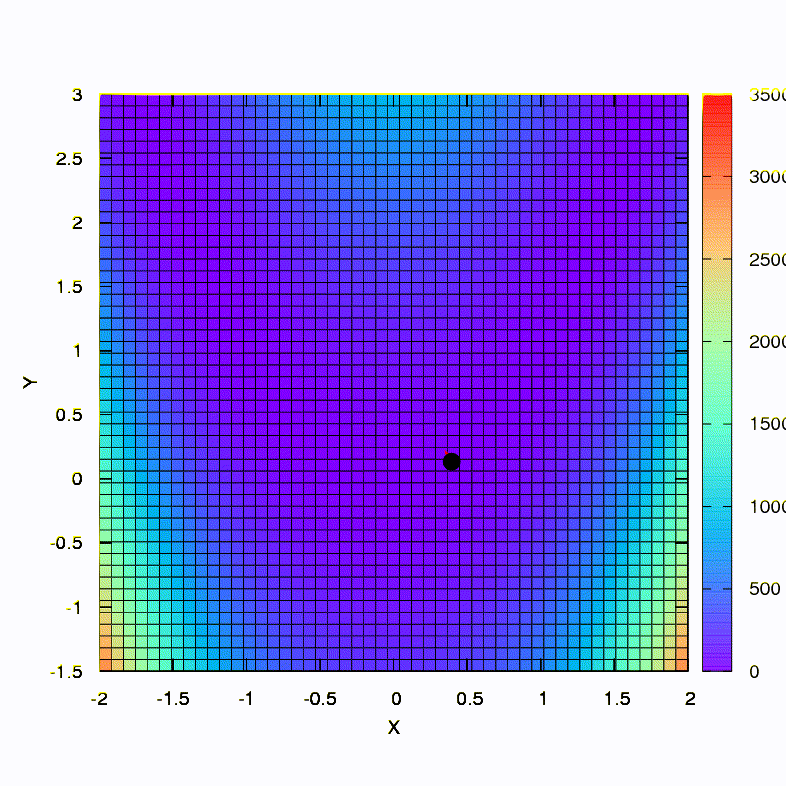
So verhält sich die Abstiegsmethode mit einem sphärischen Vertrauensbereich, es ist auch ein Gradientenabstieg. Alles ist wie ein Lehrbuch - wir stecken in einer Schlucht fest.
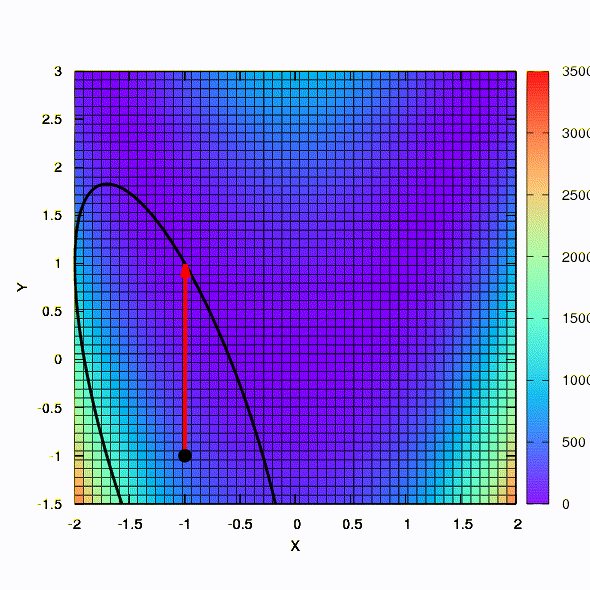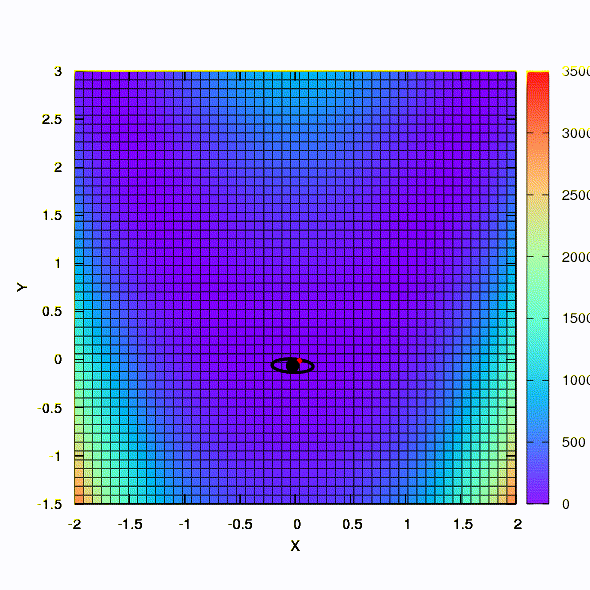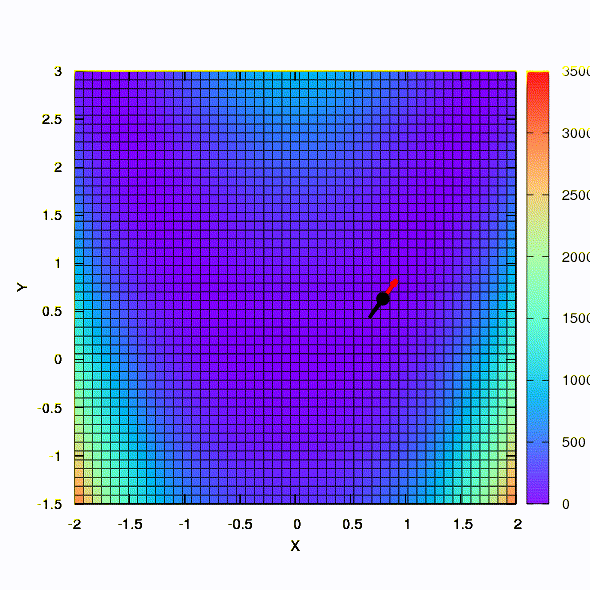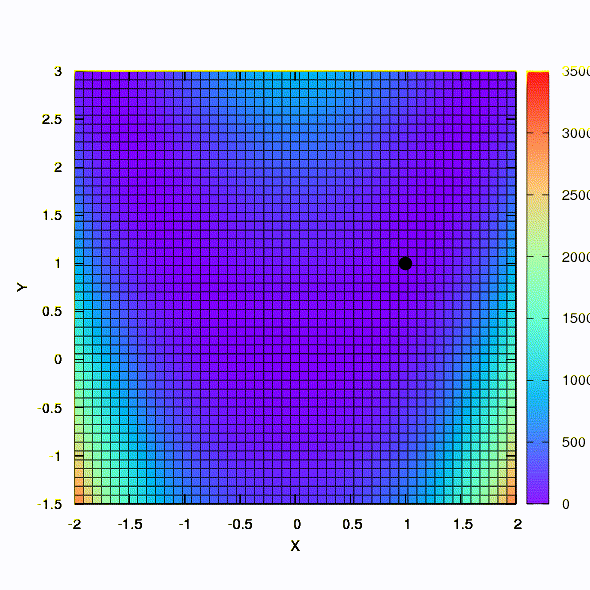
Und das bekommen wir, wenn der Konfidenzbereich die Form einer Ellipse hat, die durch die hessische Matrix definiert ist. Dies ist nichts weiter als eine Iteration der gedämpften Newton-Methode.
Nur die Frage, was zu tun ist, wenn die hessische Matrix nicht eindeutig positiv ist, blieb ungelöst. Es gibt viele Möglichkeiten. Das erste ist zu punkten. Vielleicht haben Sie Glück und Newtons Iterationen konvergieren ohne diese Eigenschaft. Dies ist sehr real, insbesondere in den letzten Phasen des Minimierungsprozesses, wenn Sie bereits nahe genug an einer Lösung sind. In diesem Fall können Iterationen der Standard-Newton-Methode verwendet werden, ohne sich um die Suche nach einer für den Abstieg zulässigen Nachbarschaft zu kümmern. Oder verwenden Sie im Fall von Iterationen der gedämpften Newton-Methode
Das heißt, wenn die erhaltene Richtung nicht die Abstiegsrichtung ist, ändern Sie sie beispielsweise in einen Anti-Gradienten.
Sie müssen nur nicht explizit prüfen, ob der Hessische nach dem Sylvester-Kriterium eindeutig positiv ist , wie hier gemacht
wurde !!! . Es ist verschwenderisch und sinnlos.
Bei subtileren Methoden wird eine Matrix konstruiert, die der hessischen Matrix nahe kommt, aber die Eigenschaft der positiven Bestimmtheit besitzt, insbesondere durch Korrektur von Eigenwerten. Ein separates Thema sind die quasi-Newtonschen Methoden oder variablen metrischen Methoden, die die positive Bestimmtheit der Matrix B garantieren und keine Berechnung der zweiten Ableitungen erfordern. Im Allgemeinen geht eine ausführliche Diskussion dieser Themen weit über den Rahmen dieses Artikels hinaus.
Ja, und übrigens folgt aus dem Gesagten, dass
die Newton-gedämpfte Methode mit positiver Bestimmtheit des Hessischen eine Gradientenmethode ist . Sowie quasi-Newtonsche Methoden. Und viele andere, basierend auf einer separaten Wahl der Richtung und Schrittgröße. Daher ist es falsch, die Newton-Methode der Gradiententerminologie gegenüberzustellen.
Zusammenfassend
Die Newton-Methode, an die bei der Erörterung von Minimierungsmethoden häufig erinnert wird, ist normalerweise nicht die Newton-Methode im klassischen Sinne, sondern die Abstiegsmethode mit der vom Hessischen der Zielfunktion angegebenen Metrik. Und ja, es konvergiert global, wenn der Hessische überall positiv bestimmt ist. Dies ist nur für konvexe Funktionen möglich, die in der Praxis viel seltener sind als wir möchten. Daher garantiert die Anwendung der Newton-Methode (wir werden uns nicht vom Kollektiv lösen und es weiterhin so nennen) im allgemeinen Fall ohne die entsprechenden Modifikationen nicht das richtige Ergebnis. Das Erlernen neuronaler Netze, auch flacher, führt normalerweise zu nicht konvexen Optimierungsproblemen mit vielen lokalen Minima. Und hier ist ein neuer Hinterhalt. Newtons Methode konvergiert normalerweise schnell (wenn sie konvergiert). Ich meine sehr schnell. Und das ist seltsamerweise schlecht, weil wir in mehreren Iterationen zu einem lokalen Minimum kommen. Und es kann für Funktionen mit komplexem Gelände viel schlimmer sein als das globale. Der Gradientenabstieg mit linearer Suche konvergiert viel langsamer, überspringt jedoch eher die Rippen der Zielfunktion, was in den frühen Stadien der Minimierung sehr wichtig ist. Wenn Sie den Wert der Zielfunktion bereits gut reduziert haben und sich die Konvergenz des Gradientenabfalls erheblich verlangsamt hat, kann eine Änderung der Metrik den Prozess durchaus beschleunigen, dies gilt jedoch für die Endphase.
Natürlich ist dieses Argument nicht universell, nicht unbestreitbar und in einigen Fällen sogar falsch. Ebenso wie die Aussage, dass Gradientenmethoden bei Lernproblemen am besten funktionieren.