Interaktives Labor für Thermodynamik als effektives Mittel für das Simulationstraining

Einführung

Simulationstraining mit multimedialen Bildungsressourcen ist einer der vielversprechenden Bereiche der Informatisierung moderner Bildung. Mit Simulationstraining ist ein Trainingsmodell gemeint, bei dem physikalische Prozesse und Bedingungen, die denen real ähneln, jedoch eine Reihe idealisierter Eigenschaften aufweisen, mithilfe von Software virtuell reproduziert werden. Die Möglichkeit der interaktiven Interaktion mit einem virtuellen Modell eines bestimmten physischen Prozesses kann den Abstraktionsgrad des Wissens über diesen Prozess erheblich verringern, was zu einer höheren Effizienz beim Erhalten und Assimilieren dieses Wissens durch eine Person führt [1] .

Untersuchungsgegenstand und Problemstellung

Als Untersuchungsgegenstand betrachten wir einen der wichtigsten Zweige der allgemeinen Physik - die klassische Thermodynamik. Im Rahmen von Bildungsaktivitäten wird das Wissen in dieser Disziplin in verschiedenen Formen vermittelt: Die wichtigsten sind: konsolidiertes theoretisches Material in Form von Vorlesungen und Lehrbüchern; praktische Aufgaben in Form von Aufgabensammlungen und Tests; Laborworkshop in Form von Richtlinien für die Durchführung von Laborexperimenten zu den Themen der Grundtheorie. Die aufgeführten Unterrichtsformen unterscheiden sich im Abstraktionsgrad der übermittelten Informationen und bilden zusammen das vollständigste Bild des Wissens in der untersuchten Disziplin.

Die anspruchsvollste Form des Wissens in Bezug auf Methodik und technische Umsetzung ist ein Laborworkshop. Zu diesem Zweck werden an Universitäten und Hochschulen speziell ausgestattete Schulungslabors eingerichtet, die die Anforderungen des Bildungsprozesses vollständig erfüllen. Der rechtzeitige Zugang zu diesen Labors erfolgt in der Regel, wenn die Schüler eine Vollzeitausbildung absolvieren. Die Fähigkeit, in Bildungslabors zu arbeiten, ist untrennbar mit der Notwendigkeit der physischen Anwesenheit des Studenten auf dem Laborgelände sowie den hohen Kosten für die Wartung und Instandhaltung des Labors unter Bedingungen seines intensiven Betriebs verbunden.

Wenn ein Schüler Fernunterricht oder Offline-Lernen ohne die Hilfe einer Bildungsorganisation absolviert, fehlt die Fähigkeit, Laborexperimente durchzuführen, häufig vollständig. Wie die Praxis zeigt, lernt der Schüler in diesem Fall Laborexperimente durch Videos oder Animationen kennen, die (wenn möglich) im öffentlichen Bereich des Internets zu finden sind. Dies ist eine ineffektive Methode, um das erforderliche Lehrmaterial zu studieren, da es an Interaktivität und Struktur des Materials mangelt und häufig sprachliche Einschränkungen aufweist Qualität des vorgestellten Materials.

In Anbetracht des Vorstehenden besteht eine dringende Aufgabe für Entwickler multimedialer Bildungsressourcen darin, ein solches Lernwerkzeug zu schaffen, das dem Bildungsprozess alle notwendigen Funktionen für die Durchführung experimenteller Arbeiten bietet, strukturiertes methodisches Material enthält und zur effektiven Assimilation von Wissen in einem bestimmten Studienbereich beiträgt. Auf der technischen Seite sollte dieses Schulungswerkzeug die Flexibilität haben, in verschiedene Fernlernsysteme (in Form von Webanwendungen und Softwarekomponenten) integriert zu werden, die Fähigkeit, auf mobilen Geräten und PCs ausgeführt zu werden, eine hohe Leistung und eine einfache Verwaltung.

Eine beispielhafte Implementierung eines Simulationsmodells eines Laborexperiments

Betrachten Sie das Laborexperiment "Reale Gase und der Phasenübergangspunkt" aus dem Kurs der Thermodynamik für Schüler und ältere Schüler von weiterführenden Schulen. Der Zweck dieses Experiments besteht darin, das reale Gas (Schwefelhexafluorid SF6) zu quantifizieren und seinen Phasenübergangspunkt zu bestimmen. Die Laborerfahrung wird an einem von 3B Scientific hergestellten Laboraufbau (Abbildung 1) durchgeführt [2] .


Abbildung 1 - Aussehen eines natürlichen Analogons eines Laboraufbaus zur Bestimmung des Phasenübergangspunkts eines realen Gases

Der vorgestellte Laboraufbau ist mit einem Gastank, einem Manometer zur Messung des Gasdrucks im Tank, einem beweglichen Kolben mit einem Schraubmechanismus und einer Waage, einem Ventilsystem und einem elektronischen Thermometer zur Messung der Gastemperatur ausgestattet. Die Drehung des Schwungrades verschiebt den Kolben, was wiederum das freie Volumen des Gasspeichers verändert. Der Arbeitsteil des Gasspeichers besteht aus durchscheinendem Material, mit dem Sie den Zustand der Testsubstanz während des Experiments visuell beobachten können.

Der Phasenübergangspunkt eines realen Gases ist durch kritische Temperatur, kritischen Druck und kritische Dichte gekennzeichnet. Unterhalb der kritischen Temperatur befindet sich die Substanz bei großen Volumina in einem gasförmigen Zustand und bei kleinen Volumina in einem flüssigen Zustand. Bei Zwischenvolumina kann es als Gemisch aus Flüssigkeit und Gas vorliegen, bei dem eine Volumenänderung unter isothermen Bedingungen eine Änderung des Aggregatzustands bewirkt: Die Gasfraktion nimmt mit zunehmendem Volumen zu und der Druck des Gemisches bleibt konstant. Da Flüssigkeiten und Dämpfe unterschiedliche Dichten haben, werden sie im Gravitationsfeld getrennt. Mit steigender Temperatur nimmt die Flüssigkeitsdichte ab und die Gasdichte nimmt zu, bis diese beiden Dichten dem gleichen kritischen Dichtewert entsprechen. Oberhalb der kritischen Temperatur kann das Gas nicht in einen flüssigen Zustand umgewandelt werden. Unter isothermen Bedingungen folgt das Gas jedoch nicht den Gesetzen eines idealen Gases, bis seine Temperatur signifikant über die kritische Temperatur gestiegen ist.

Der Zustand des Gases wird in Abhängigkeit von den Parametern Druck (P), Volumen (V) und Temperatur (T) anhand des Clapeyron-Phasendiagramms dargestellt. Als mathematische Grundlage des Experiments wird das Van-der-Waals-Gasmodell verwendet:

$$

$$Pr (Vr) = 8Tr / (3Vr-1) -3 / Vr ^ 2$$

wobei Pr der reduzierte Gasdruck ist, der dem Verhältnis seines tatsächlichen Drucks zum Druck am kritischen Punkt entspricht (Pr = P / Pc); Vr ist das reduzierte Gasvolumen, das dem Verhältnis seines tatsächlichen Volumens zum Volumen am kritischen Punkt entspricht (Vr = V / Vc); Tr ist die reduzierte Gastemperatur, die dem Verhältnis seiner tatsächlichen Temperatur zur Temperatur am kritischen Punkt entspricht (Tr = T / Tc).

Die Van-der-Waals-Gleichung ermöglicht die Berechnung von Isothermen (Linien gleicher Temperatur) für das Testgas in der angegebenen Form (Abbildung 2).

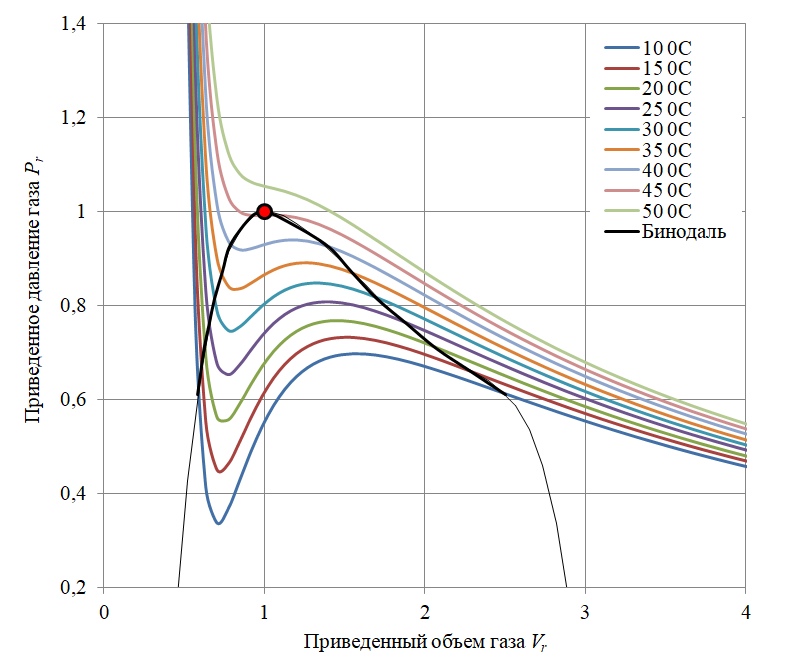Abbildung 2 - Clapeyron-Phasendiagramm für Schwefelhexafluorid SF6 ohne Dampf-Flüssigkeits-Gleichgewicht

Wie aus dem Diagramm in 2 ersichtlich ist, hat bei einer Gastemperatur unterhalb der kritischen Temperatur (Tc) die Van-der-Waals-Gleichung in dem Teil der Isotherme, in dem dPr / dVr> 0 oszillierenden Charakter hat. In diesen Bereichen liegt die Substanz in Form eines Gemisches aus Gas und Flüssigkeit vor, und in Wirklichkeit tritt Gaskondensation entlang des isobaren Pfades auf (das Volumen ändert sich bei konstantem Druck). Das Van-der-Waals-Diagramm innerhalb der sogenannten binodalen Kurve (schwarze Kurve im Diagramm) [3] beschreibt daher das Verhalten eines realen Gases nur unzureichend.

Um dieses Problem zu lösen, wurde die Maxwell-Methode für gleiche Flächen verwendet [4] , deren Kern darin besteht, den oszillierenden isothermen Abschnitt durch eine horizontale Linie (Isobare) zu ersetzen, die den durch die Isotherme beschriebenen Bereich in zwei gleich große Bereiche unterteilt (Abbildung 3).

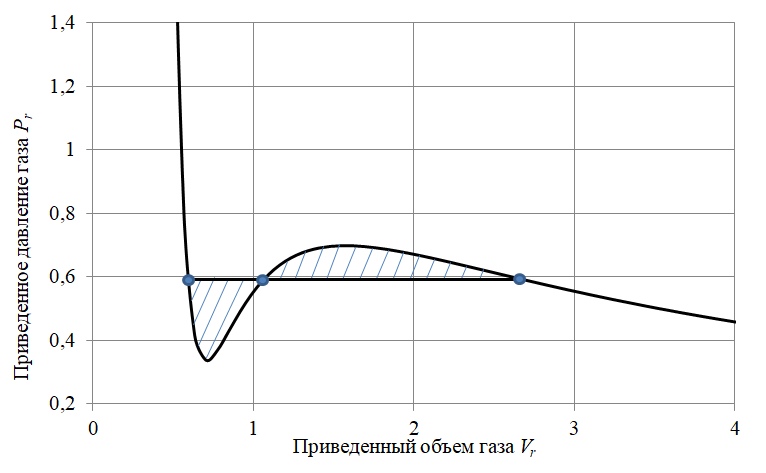Abbildung 3 - Zur Methode der gleichen Flächen von Maxwell

Unten finden Sie ein Codefragment (Matlab) zur Lösung des beschriebenen Problems [4].

function maxwell_equal_area_2 clc; clear all; close all %  Tr  Tc: Tr = T/Tc Tr = 0.9; %    Pr (  --) Prfh = @(Vr) 8/3*Tr./(Vr - 1/3) - 3./(Vr.^2); %    Vr = linspace(0.5,4,100); %    Pr = Prfh(Vr); 

Um die Flächen zweier Regionen zu berechnen, die durch Isotherme und Isobare gebildet werden, müssen die drei Wurzeln der Polynomgleichung gefunden werden:

$$

$$Vr ^ 3- (1 + 8Tr / Pr) / 3 + 3 / Pr-1 / Pr = 0$$

 %    vdWp = [1 -1/3*(1+8*Tr/y) 3/y -1/y]; %     v = sort(roots(vdWp)) %  A1 (       ) A1 = (v(2)-v(1))*y - quad(Prfh,v(1),v(2)) %  A2 (       ) A2 = quad(Prfh,v(2),v(3)) - (v(3)-v(2))*y % ,  ,  ,  A1=A2 Pr_equal_area = fzero(@equalArea, 0.65) 

Die Ergebnisse der Berechnungen können im Diagramm angezeigt werden (Abbildung 4).

 xx = [v(1) Vr(Vr >= v(1) & Vr <= v(2)) v(2)]; yy = [Prfh(v(1)) Pr(Vr >= v(1) & Vr <= v(2)) Prfh(v(2))]; lightgray = [0.9 0.9 0.9]; fill(xx,yy,lightgray) xx = [v(2) Vr(Vr >= v(2) & Vr <= v(3)) v(3)]; yy = [Prfh(v(2)) Pr(Vr >= v(2) & Vr <= v(3)) Prfh(v(3))]; fill(xx,yy,lightgray) %      text(v(1),1,sprintf('A1 = %f',A1)) text(v(3),1,sprintf('A2 = %f',A2)) 

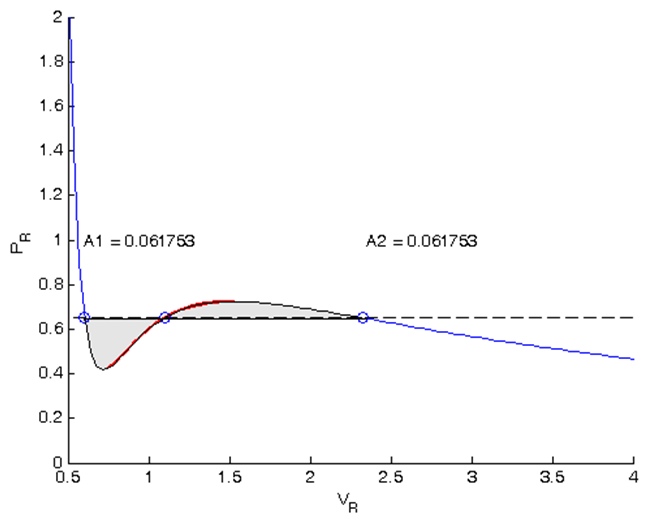Abbildung 4 - Ergebnisse der Isobarenberechnung nach der Methode gleicher Maxwell-Flächen in Matlab

Die endgültige Form der Funktion für die flächengleiche Methode:

 function Z = equalArea(y) Tr = 0.9; vdWp = [1 -1/3*(1+8*Tr/y) 3/y -1/y]; v = sort(roots(vdWp)); Prfh = @(Vr) 8/3*Tr./(Vr - 1/3) - 3./(Vr.^2); A1 = (v(2)-v(1))*y - quad(Prfh,v(1),v(2)); A2 = quad(Prfh,v(2),v(3)) - (v(3)-v(2))*y; Z = A1 - A2; % :  ; :  

Das endgültige mathematische Modell des Experiments wird daher durch das Clapeyron-Diagramm für Schwefelhexafluorid unter Berücksichtigung der Bedingungen des Dampf-Flüssigkeits-Gleichgewichts dargestellt (Abbildung 5).


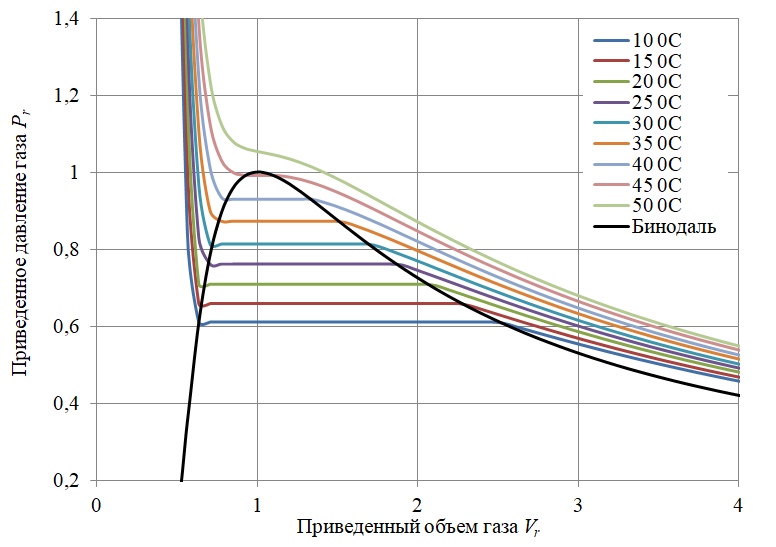Abbildung 5 - Clapeyron-Phasendiagramm für Schwefelhexafluorid SF6 unter Berücksichtigung des Dampf-Flüssigkeits-Gleichgewichts

Neben der mathematischen Komponente enthält das Simulationsmodell des Experiments eine Reihe grafischer Objekte, die die Laborausrüstung visuell widerspiegeln (Abbildung 6).


Abbildung 6 - Grafisches Modell eines Laboraufbaus: 1 - Manometer; 2 - Zirkulationsthermostat; 3 - elektronisches Thermometer; 4 - Gastank; 5 - Lautstärkeregler; 6 - Gasfüllventil

Dynamisch erzeugte Fehler, die transiente (instationäre) Prozesse, Messungenauigkeiten, Empfindlichkeit der Kontrollen usw. simulieren, werden zu den gemessenen Werten im Versuchsausführungsmodus hinzugefügt. Das Simulationsmodell bietet eine vollständige Beobachtung des physikalischen Prozesses mit der Möglichkeit, die Eingabeparameter und experimentellen Bedingungen zu ändern.

Eine beispielhafte Implementierung eines virtuellen Laborworkshops

Basierend auf dem oben beschriebenen Beispiel der Methodik zur Berechnung von Simulationsmodellen physikalischer Prozesse unter Verwendung der übergeordneten Programmiersprache AppGameKit wurde ein interaktiver Laborworkshop für klassische Thermodynamik entwickelt, der die Hauptthemen des Kurses abdeckt: interne Energie, Gasgesetze, Wärmeübertragung, Wärmeausdehnung, thermodynamische Zyklen. Diese Entwicklung ist für Laborexperimente ohne echte Laborausrüstung vorgesehen. Laborinstallationen werden in Übereinstimmung mit ihren tatsächlichen Gegenstücken hergestellt. Jede Laborarbeit enthält kurze Richtlinien und Referenzinformationen, die für die Verarbeitung experimenteller Daten erforderlich sind.

Eine Besonderheit des virtuellen Labors ist seine ergänzende Flexibilität aufgrund der Unterstützung mehrerer Plattformen. Simulationslaborarbeiten sind auf PCs, Mobilgeräten und in einer Webbrowser-Umgebung möglich (ohne dass Software auf dem Gerät eines Benutzers installiert werden muss). Die vorgestellte Lösung verwendet einen einzigartigen Algorithmus zum Laden einer grafischen 3D-Szene in den Speicher unter Verwendung eines eigenen Binärdatenformats, wodurch die Rekonstruktionszeit von 3D-Modellen in der Spiel-Engine auf einige Sekunden reduziert werden kann. Dies ist ein wichtiger Faktor beim Ausführen des Programms auf Mobilgeräten.

Abbildung 7 zeigt einen Screenshot des virtuellen Labors, das im Microsoft Edge-Webbrowser ausgeführt wird und vollständige Hardwareunterstützung für 3D-Grafiken auf Basis des HTML5-Standards und der WebGL-Technologie bietet.


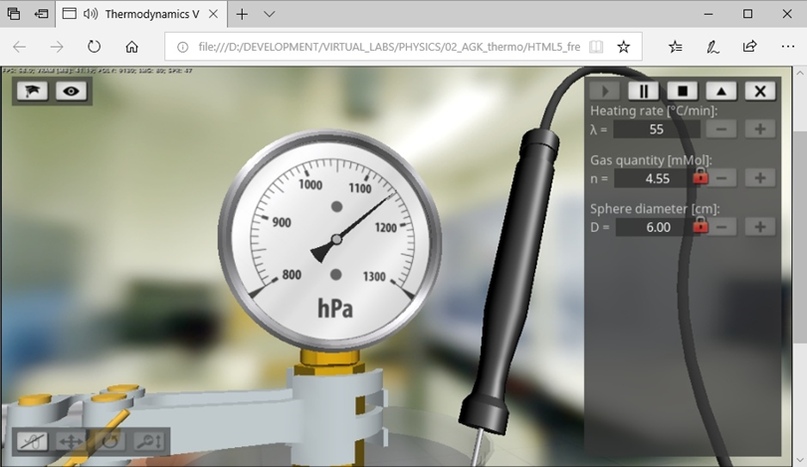Abbildung 7 - Ausführen eines virtuellen Labors in einem Microsoft Edge-Webbrowser

Im Folgenden finden Sie die Online-Versionen der Laborarbeit, für die die Verwendung des Microsoft Edge-Webbrowsers empfohlen wird, der Teil des Microsoft Windows 10-Betriebssystems ist:

1. Interne Energie und mechanische Arbeit
2. Interne Energie und elektrischer Strom
3. Boyle-Marriott-Gesetz
4. Homosexuell Lussac Gesetz
5. Luft Adiabat
6. Reale Gase und Phasenübergangspunkt
7. Leslie Cube
8. Wärmeleitfähigkeit
9. Wärmeausdehnung von Feststoffen
10. Wasseranomalie
11. Stirlingmotor Modell D.
12. Stirlingmotor Modell G.
13. Wärmepumpen

Um Laborarbeiten auf einem mobilen Gerät (Smartphone oder Tablet) basierend auf dem Android-Betriebssystem durchzuführen, können Sie die mobile Anwendung des virtuellen Labors herunterladen.

Fazit

Das in diesem Artikel beschriebene Beispiel für die Implementierung des Simulationstrainingswerkzeugs auf der Grundlage des virtuellen Labors für Thermodynamik zeigt die Möglichkeit, den Bildungsprozess durch ein methodisches Hilfswerkzeug zu ergänzen, das die Anforderungen und Standards der modernen allgemeinen und höheren Bildung erfüllt. Das verallgemeinerte Konzept der Entwicklung multimedialer Bildungsressourcen umfasst eine Reihe von Hauptphasen: Festlegung der tatsächlichen methodischen Komponente der Laborwerkstatt (einschließlich der Auswahl wirksamer Laborgeräte sowie ihrer Referenz und methodischen Unterstützung); Entwicklung eines numerischen Simulationsmodells des Experiments; Implementierung der grafischen Komponente eines Simulationslabor-Workshops; Implementierung der Softwarekomponente eines Simulationslabor-Workshops; Integration eines Simulationslabor-Workshops in den Bildungsprozess (Einführung der Entwicklung in einen bestehenden Schulungskurs oder Erstellung eines neuen Schulungskurses für die Arbeit mit einem Simulationslabor-Workshop).

Einer der vielversprechenden Bereiche der Entwicklung der Simulationsausbildungstechnologie ist derzeit die Implementierung von Multi-Agent-Trainingssystemen, deren Betrieb auf den Algorithmen zur Generierung individueller Bildungspfade mit dynamischer Bildung von Bildungsinhalten basiert. Solche Systeme bieten eine adaptive Einstellung der Lernumgebung unter Berücksichtigung der individuellen Merkmale des Benutzerprofils. Mit diesen Algorithmen erhalten Sie: für Schüler - einen personalisierten Plan, Inhalt, Methodik und E-Learning-Tools; für Lehrer - innovative Technologien für den Unterricht und die Analyse gebildeter Kompetenzen, für Schulen und Universitäten - ein modernes Modell für das Management von Bildungsprozessen.

Literaturhinweise

1. Virtuelle Labore und technische Simulationen
2. Laborausstattung 3B Scientific
3. Methode zur Berechnung binodaler Kurven
4. Flächengleichheitsmethode für die Van-der-Waals-Gleichung