Der Levenberg-Marquardt-Algorithmus ist einfach. Der Levenberg-Marquardt-Algorithmus ist effizient.
Und sie sagen über ihn, dass er irgendwo zwischen dem Gefälle und der Newton-Methode liegt, was auch immer das bedeutet. Nun, es ist irgendwie mit Newtons Methode und seiner Verbindung mit dem Gradientenabstieg geregelt. Aber was meinen sie, wenn sie diesen tiefen Satz aussprechen? Lass uns einen kleinen Schleicher versuchen.
In seinen Artikeln beschreibt Genosse Levenberg [K. Eine Methode zur Lösung bestimmter Probleme auf den letzten Quadraten. Quart. Appl. Mathe. 1944. Vol. 2. S. 164-168.] Und nach ihm Bürger Marquardt [Marquardt, Donald (1963). "Ein Algorithmus zur Schätzung kleinster Quadrate nichtlinearer Parameter." SIAM Journal für Angewandte Mathematik. 11 (2): 431–441.] Betrachtet das Problem der kleinsten Quadrate, das so aussieht:
,
was einfacher in Vektorform geschrieben werden kann
.
Und Sie können es noch einfacher machen, indem Sie vollständig auf den kleinsten Feldern punkten. Dies hat keinen Einfluss auf die Geschichte.
Das Problem wird also berücksichtigt
.
Ein solches Problem tritt so oft auf, dass die Wichtigkeit, eine wirksame Methode zu seiner Lösung zu finden, kaum überschätzt werden kann. Aber wir werden von einem anderen ausgehen. In einem früheren Artikel wurde gezeigt, dass das bekannte Gradientenabstiegsverfahren und nicht nur es aus den folgenden Überlegungen erhalten werden kann. Nehmen wir an, wir kommen zu einem bestimmten Punkt
in denen die minimierte Funktion wichtig ist
. Wir definieren an dieser Stelle eine Hilfsfunktion
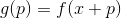
sowie einige seiner Modelle
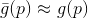
. Für dieses Modell stellen wir ein Hilfsproblem dar
wo
- eine bestimmte vorgegebene Menge zulässiger Werte, die so gewählt werden, dass das Problem eine einfache Lösung und Funktion hat
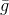
ziemlich genau angenähert
auf
. Dieses Schema wird als Trust-Region-Methode bezeichnet, und viele
auf dem der Wert der Modellfunktion minimiert wird - der Konfidenzbereich dieser Funktion. Für den Gefälleabstieg haben wir genommen
für Newtons Methode
und als Modell für
der lineare Teil der Taylor-Expansion
.
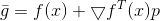
Mal sehen, was passiert, wenn wir das Modell durch die Aufnahme komplizieren
.
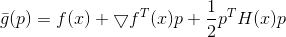
Wir minimieren diese Modellfunktion in einem elliptischen Konfidenzbereich
(Multiplikator zur leichteren Berechnung hinzugefügt). Bei Anwendung der Lagrange-Multiplikatormethode erhalten wir das Problem
,
deren Lösung die Gleichheit erfüllt
oder
Im Gegensatz zu dem, was wir zuvor bei Verwendung des linearen Modells gesehen haben, hängt die Richtung
p hier
nicht nur von
der Metrik ab 
, sondern auch über die Wahl der
Größe der Vertrauensregion 
Dies bedeutet, dass die lineare Suchtechnik (zumindest vernünftigerweise) nicht anwendbar ist. Es stellt sich auch als schwierig heraus, den Wert explizit zu bestimmen
entsprechend
. Es ist jedoch offensichtlich, dass mit einer Zunahme
Länge
wird abnehmen. Wenn wir die Bedingung jedoch immer noch auferlegen
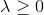
Dann ist die Schrittlänge nicht größer als die, die Newtons Methode ergeben würde (modisch, ohne Modifikationen und Bedingungen).
Also können wir stattdessen für eine gegebene
Suche nach dem richtigen Wert
, mache genau das Gegenteil: finde das
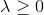
unter denen die Bedingung
. Dies ist in diesem Fall eine Art Ersatz für die späte Suche. Marquardt schlug das folgende einfache Verfahren vor:
- wenn für einen Wert Zustand
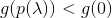fertig dann wiederholen 
bis 
- wenn
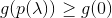dann akzeptiere 
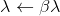und wiederholen.
Hier
und
Sind Konstanten, die Methodenparameter sind. Multiplikation mit
entspricht der Erweiterung des Vertrauensbereichs und der Multiplikation mit
- seine Verengung.
Die angegebene Technik kann auf
jede Zielfunktion angewendet werden. Beachten Sie, dass hier die positive Bestimmtheit des Hessischen nicht mehr erforderlich ist, im Gegensatz zu dem zuvor betrachteten Fall, als die Newton-Methode als Sonderfall der sequentiellen Abstiegsmethode vorgestellt wurde. Nicht einmal seine Nichtentartung ist erforderlich, was in einigen Fällen sehr wichtig ist. In diesem Fall steigt jedoch der Preis für die Richtungssuche seit jeder Änderung
führt zu der Notwendigkeit, ein lineares System zu lösen, um zu bestimmen
.
Mal sehen, was passiert, wenn wir diesen Ansatz auf das Problem der kleinsten Quadrate anwenden.
Verlaufsfunktion
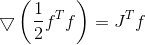
ihr Hessisch
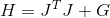
wo
. Ersetzen und erhalten Sie das folgende System, das die Richtung der Suche bestimmt
.
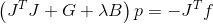
Es ist durchaus akzeptabel, aber die Berechnung der zweiten Ableitungen einer Vektorfunktion kann recht teuer sein. Marquardt schlug vor, die Funktion selbst zu verwenden, um dieses Problem zu umgehen.
und seine lineare Approximation
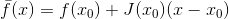
bei dem die Matrix
dreht sich auf Null. Wenn jetzt als
nimm die Identitätsmatrix
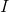
Dann erhalten wir die Standardform der Levenberg-Marquardt-Methode zur Lösung des Problems der kleinsten Quadrate:
.
Für diese Methode zur Bestimmung der Abstiegsrichtung hat Marquardt den Satz mit Aspiration bewiesen
in die unendliche Richtung
neigt zum Anti-Gradienten. Der interessierte Leser kann im Basisartikel einen strengen Beweis finden, aber ich hoffe, dass diese Aussage selbst aus der Logik der Methode ziemlich offensichtlich geworden ist. Bis zu einem gewissen Grad rechtfertigt dies den allgegenwärtigen Hinweis darauf, dass wir mit einem Anstieg des Lambda (den ich aus irgendeinem Grund oft als Regularisierungsparameter bezeichne) einen Gradientenabstieg erhalten. Eigentlich nichts dergleichen - wir würden es nur im Grenzbereich bekommen, genau dort, wo die Schrittlänge gegen Null geht. Es ist viel wichtiger, dass bei einem ausreichend großen Lambda-Wert die Richtung, die wir erhalten, die
Abstiegsrichtung ist , was bedeutet, dass wir die
globale Konvergenz der Methode erhalten . Und hier ist der zweite Teil der Aussage, dass, wenn das Lambda gegen Null geht, wir die Newton-Methode erhalten, dies eindeutig wahr ist, aber nur, wenn wir stattdessen akzeptieren
seine lineare Annäherung
.
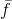
Es scheint, dass alle. Wir minimieren die Norm der Vektorfunktion in der elliptischen Metrik - wir verwenden den Levenberg-Marquardt. Wir haben es mit einer Funktion einer allgemeinen Form zu tun und können die Matrix der zweiten Ableitungen berechnen - verwenden Sie für Wells die Methode der allgemeinen Region Konfidenzregion. Aber es gibt Perverse ...
Manchmal die Levenberg-Marquardt-Methode, um die Funktion zu minimieren
sie nennen einen Ausdruck wie diesen:
.
Alles scheint gleich zu sein, aber hier
- Matrix der Sekunde! abgeleitete Funktionen
. Formal hat dies ein Existenzrecht, aber es ist eine Perversion. Und hier ist warum. Der gleiche Marquardt schlug in seinem Artikel eine Methode zur Lösung eines Gleichungssystems vor
durch Minimierung der Funktion
die beschriebene Methode. Wenn als
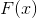
Nehmen Sie den Gradienten der Zielfunktion, dann erhalten wir wirklich den reduzierten Ausdruck. Und die Perversion ist weil
Das Minimierungsproblem, das durch das System nichtlinearer Gleichungen erzeugt wird, das durch das Minimierungsproblem erzeugt wird, ist gelöst .
Doppelschlag. Ein solcher Ausdruck ist zumindest nicht besser als die erste Gleichung eines sphärischen Vertrauensbereichs, aber im Allgemeinen sowohl unter dem Gesichtspunkt der Produktivität (unnötige Multiplikationsoperationen und bei normalen Implementierungen - Faktorisierung) als auch unter dem Gesichtspunkt der Methodenstabilität (die Matrixmultiplikation an sich verschlechtert sich) viel schlechter seine Konditionierung). Es wird manchmal beanstandet, dass
garantiert positiv definiert, aber in diesem Fall spielt es keine Rolle. Betrachten wir die Levenberg-Marquardt-Methode aus der Perspektive der sequentiellen Abstiegsmethode. In diesem Fall stellt sich heraus, dass wir die Matrix als Metrik verwenden möchten
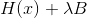
und damit sie in dieser Eigenschaft handeln kann, die Bedeutung
sollte seine positive Sicherheit gewährleisten. Angesichts dessen
positiver bestimmter Wert
kann immer gefunden werden - und daher keine Notwendigkeit von verlangen
positive Sicherheit wird nicht beobachtet.
Als Matrix
Es ist nicht erforderlich, eine Einheit zu nehmen, aber für ein quadratisches Modell der Zielfunktion ist die Angabe eines angemessenen Konfidenzbereichs nicht mehr so einfach wie für ein lineares Modell. Wenn wir die durch das Hessische induzierte elliptische Region nehmen, dann degeneriert die Methode in die Newtonsche Methode (na ja, fast)
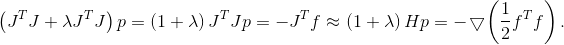
Es sei denn natürlich, die hessische Matrix ist eindeutig positiv. Wenn nicht, können Sie nach wie vor das korrigierte Hessische als Metrik oder eine Matrix verwenden, die in gewissem Sinne nahe daran liegt. Es gibt auch eine Empfehlung, eine Matrix als Metrik zu verwenden
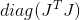
, was durch die Konstruktion garantiert positiv definitiv ist. Leider kenne ich zumindest keine strenge Rechtfertigung für diese Wahl, aber sie wird ziemlich oft als empirische Empfehlung erwähnt.
Lassen Sie uns zur Veranschaulichung sehen, wie sich die Methode auf derselben Rosenbrock-Funktion verhält, und wir werden sie in zwei Formen betrachten - als einfache Funktion, die in der Form geschrieben ist
,
und als Problem der kleinsten Quadrate
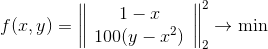
So verhält sich eine Methode mit einem sphärischen Vertrauensbereich.
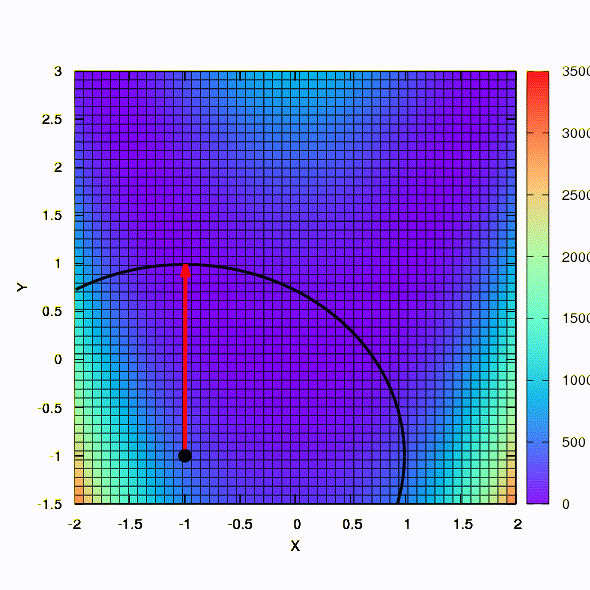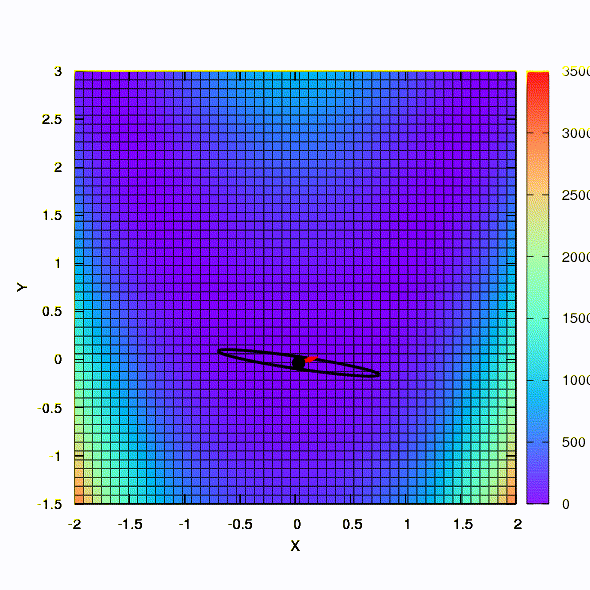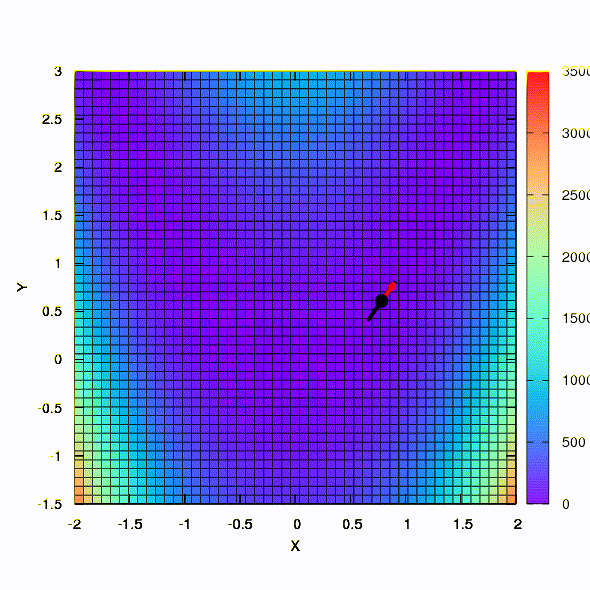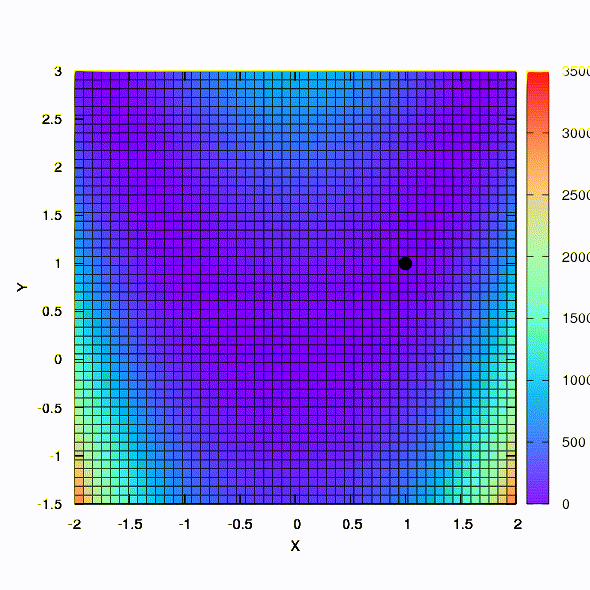
Die gleiche Methode verhält sich also, wenn die Form des Konfidenzbereichs durch eine Matrix gegeben ist, die gemäß der Davidon-Fletcher-Powell-Regel erstellt wurde. Die Konvergenz wirkt sich aus, ist jedoch viel bescheidener als im ähnlichen Fall, wenn das lineare Modell der Zielfunktion verwendet wird.
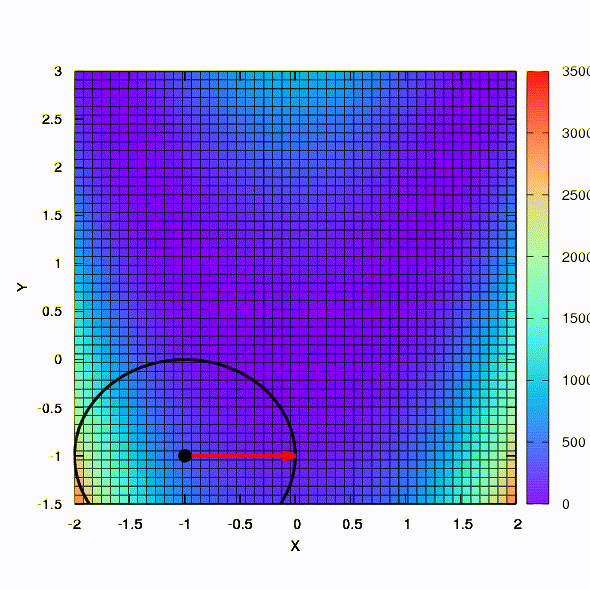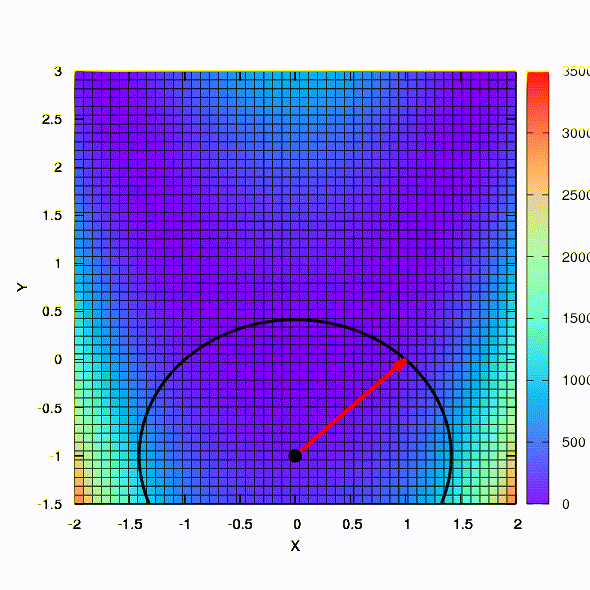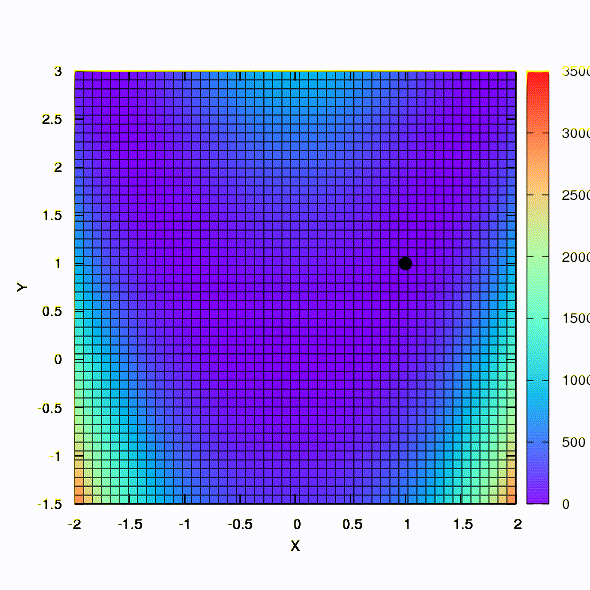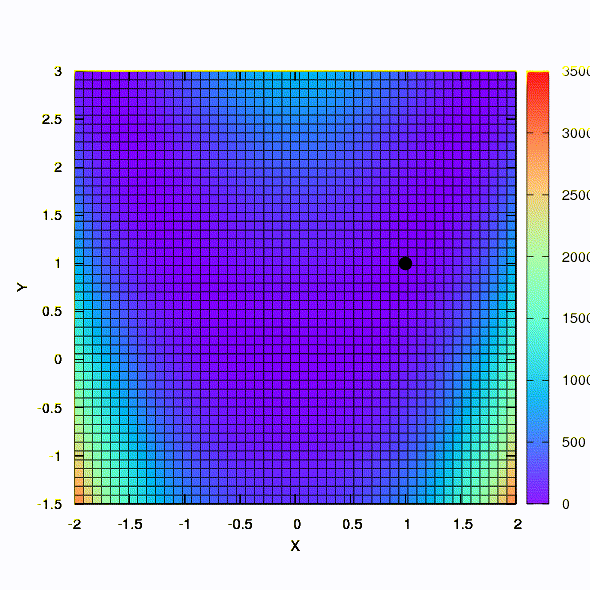
Und dies ist das Verhalten der Methode, die auf das Problem der kleinsten Quadrate angewendet wird. Es konvergiert in 5 Iterationen.
Ziehen Sie bitte
nicht aus dieser Schlussfolgerung, dass die zweite Formulierung für Funktionen dieser Art immer besser ist als die erste . Dies ist nicht so, es ist nur in diesem speziellen Fall passiert.
Fazit
Die Levenberg-Marquardt-Methode ist meines Wissens die erste Methode, die auf der Idee einer vertrauensvollen Region basiert. Er hat sich in der Praxis sehr gut gezeigt, als er das Problem der kleinsten Quadrate gelöst hat. Die Methode konvergiert in den meisten Fällen (von mir gesehen) ziemlich schnell (ich habe in einem früheren Artikel gesagt, ob es gut oder schlecht ist). Obwohl allgemeine Funktionen minimiert werden, ist es kaum die beste Option, eine Kugel als vertrauenswürdige Region auszuwählen. Ein wesentlicher Nachteil des Verfahrens (in seiner hier beschriebenen Grundformulierung) besteht außerdem darin, dass die Größe des Konfidenzbereichs implizit festgelegt wird. Der Nachteil ist, dass man die Bedeutung kennt
Wir können natürlich zum aktuellen Zeitpunkt zählen
Berechnen Sie einfach die Schrittlänge
. Wenn wir jedoch zu einem neuen Punkt wechseln, wird derselbe Wert verwendet
Ein völlig anderer Wert des Vertrauensbereichs wird bereits entsprechen. Somit verlieren wir die Fähigkeit, die Größe des Konfidenzbereichs „Merkmal für die Aufgabe“ zu bestimmen, und sind gezwungen, seine Größe an jedem neuen Punkt auf neue Weise zu bestimmen. Dies kann von Bedeutung sein, wenn für die Konvergenz eine ausreichend große Anzahl von Iterationen erforderlich ist und die Berechnung des Werts einer Funktion teuer ist. Ähnliche Probleme werden mit fortgeschritteneren Methoden gelöst, die auf der Idee einer vertrauensvollen Region basieren.
Aber das ist eine ganz andere Geschichte.
Ergänzung
Dank der wertvollen Kommentare von
Dark_Daiver habe ich beschlossen, das Obige durch die folgende Bemerkung zu ergänzen. Natürlich kann man die Levenberg-Marquardt-Methode auf eine andere, rein empirische Weise erreichen. Kehren wir nämlich zu dem im vorherigen Artikel beschriebenen Schema der sequentiellen Abstiegsmethode zurück und stellen uns erneut die Frage, ob eine angemessene Metrik für das lineare Modell der Zielfunktion erstellt werden soll.
Angenommen, die hessische Matrix am aktuellen Punkt im Suchraum ist nicht eindeutig positiv und kann nicht als Metrik dienen (um zu prüfen, ob dies der Fall ist, haben wir weder die Fähigkeit noch den Wunsch). Bezeichnen mit
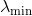
sein kleinster Eigenwert. Dann können wir den Hessischen korrigieren, indem wir einfach alle seine Eigenwerte um verschieben
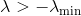
. Fügen Sie dazu einfach die Matrix zum Hessischen hinzu
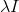
. Dann nimmt die Gleichung, die die Abstiegsrichtung bestimmt, die Form an
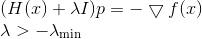
Wenn wir eine gute niedrigere Punktzahl für haben
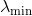
Dann können wir alles tun, was in sequentiellen Abstiegsmethoden getan wurde. Wenn wir jedoch keine solche Schätzung haben, berücksichtigen wir dies mit einem Anstieg
Wenn die Länge
p abnimmt, können wir mit Sicherheit sagen, dass es eine ausreichend große gibt
das zur gleichen Zeit
positiv bestimmt und
.
Warum ich eine solche Schlussfolgerung der Methode für nicht allzu erfolgreich halte. Erstens ist es überhaupt nicht offensichtlich, dass die auf diese Weise konstruierte Metrik für den praktischen Gebrauch geeignet ist. Es werden natürlich Informationen über die zweiten Ableitungen verwendet, aber es folgt nirgendwo, dass eine Verschiebung der Eigenwerte um einen bestimmten Wert sie nicht unbrauchbar macht. Wie der Kollege in den Kommentaren feststellte, scheint es offensichtlich, dass das Hinzufügen einer skalierten Identitätsmatrix zur hessischen Matrix dazu führt, dass der elliptische Konfidenzbereich dazu neigt, sphärisch zu sein, und auch hier (wie es scheint) die Probleme des Blockierens im Canyon und andere Freuden des Gradientenabstiegs und der engen zu ihm Methoden. In der Praxis passiert dies jedoch nicht. Auf jeden Fall konnte ich nie Beispiele beobachten, die ein solches Verhalten veranschaulichen. In diesem Fall stellt sich die Frage:
Aber warum eigentlich ?
Eine solche Frage stellt sich jedoch nicht, wenn wir diese Methode nicht als Sonderfall von Abstiegsmethoden betrachten, sondern als Konfidenzbereichsmethode mit einem quadratischen Modell der Zielfunktion, da die Antwort offensichtlich ist: Wenn das Lambda zunimmt, komprimieren wir nur die Kugel - den Konfidenzbereich für unser Modell. Informationen über die Krümmung gehen nirgendwo hin und werden von nichts ausgewaschen - wir müssen nur die Größe des Bereichs wählen, in dem das quadratische Modell die Zielfunktion angemessen beschreibt. Daraus folgt, dass es kaum wert ist, einen signifikanten Effekt von einer Änderung der Metrik, dh der Form des Vertrauensbereichs, zu erwarten, da alle Informationen, die wir über die Zielfunktion haben, bereits in ihrem Modell berücksichtigt werden.
Und zweitens ist es bei der Betrachtung einer Methode wichtig, die Hauptidee zu verstehen, die Marquardt zu dieser Methode geführt hat, nämlich die Idee einer vertrauensvollen Region. Letztendlich können wir nur verstehen, warum die numerische Methode funktioniert und, was noch wichtiger ist, warum sie möglicherweise nicht funktioniert.