RESHI.RU - ein Roboter löst und erklärt Schultextprobleme in der Mathematik

Einführung

Als ich meinem Kind in der 4. Klasse erklärte, wie man ein Textproblem in Mathematik löst, verstand ich plötzlich zwei Dinge. Erstens kann der Prozess der Erklärung der Entscheidung automatisiert werden. Und zweitens eignet sich für die meisten Computerprobleme in der Schule eine universelle Methode durch ein Gleichungssystem, das aus irgendeinem Grund in den unteren Klassenstufen der Schule noch nicht untersucht wurde. Darüber hinaus liegt die Beherrschung dieser Methode in der Macht des Mittelschülers und ermöglicht es ihm, Aufgaben zu bewältigen, die ihm zuvor nicht zugänglich waren. Das Ergebnis dieses Verständnisses war die RESHI.RU- Website mit einem Roboter, der die Aufgaben erklärte.

Der Unterschied zu zahlreichen Websites mit vorgefertigten Hausaufgaben besteht darin, dass das Problem theoretisch von jedem gelöst werden kann und nicht vorbestimmt ist. Aber nur theoretisch, da der Roboter in der Praxis nur die Arten von Aufgaben versteht, für die eine Software-Implementierung durchgeführt wurde. Bei den Aufgaben von Lehrbüchern für die 4. Klasse zeigt der Roboter 65% der richtigen Lösungen (und wenn er nicht kann oder zweifelt, warnt er ehrlich davor), für die 3. Klasse - ungefähr 80%.
Das zu lösende Problem sollte mit fehlerfreiem Text formuliert sein, keine grafischen Informationen in der Bedingung enthalten (Bilder, Diagramme) und rechnerisch sein, dh die Antwort sollte eine oder mehrere Größen sein. Die Werte im Zustand des Problems können entweder Zahlen oder Variablen sein.

Der Roboter versucht, ein System einfacher Gleichungen für das Problem zu erstellen und es zu lösen. Für einige Arten von Aufgaben kann der Roboter eine Schulmethode lösen, die als zusätzliche angeboten wird.

Das Hauptziel von RESHI.RU besteht jedoch nicht darin, bestimmte Probleme zu lösen, sondern anhand von Beispielen die universelle Methode zur Lösung durch ein System einfacher Gleichungen zu erklären.

Aufgabenbeispiel

Betrachten Sie ein Beispiel eines Roboters, der das folgende Problem auf der RESHI.RU- Website löst .

Zwei Busse verließen das Dorf und die Stadt aufeinander zu. Ein Bus fuhr 100 km mit einer Geschwindigkeit von 25 km / h zum Meeting. Wie viele Kilometer vor dem Treffen fuhr der zweite Bus, wenn seine Geschwindigkeit 50 km / h beträgt.

Der Roboter erkannte, dass dies eine Aufgabe für die Bewegung von zwei Objekten ist und er weiß, wie man solche löst. Übrig geblieben
Wählen Sie alle Größen richtig aus, verstehen Sie ihre Typen und korrelieren Sie mit diesen beiden Objekten.
Zur Erklärung zeigt der Roboter eine Folge von Abschnitten an, von denen jeder den einen oder anderen Aspekt beschreibt, näher am Erhalt einer Antwort. Hier sind Screenshots dieser Abschnitte.









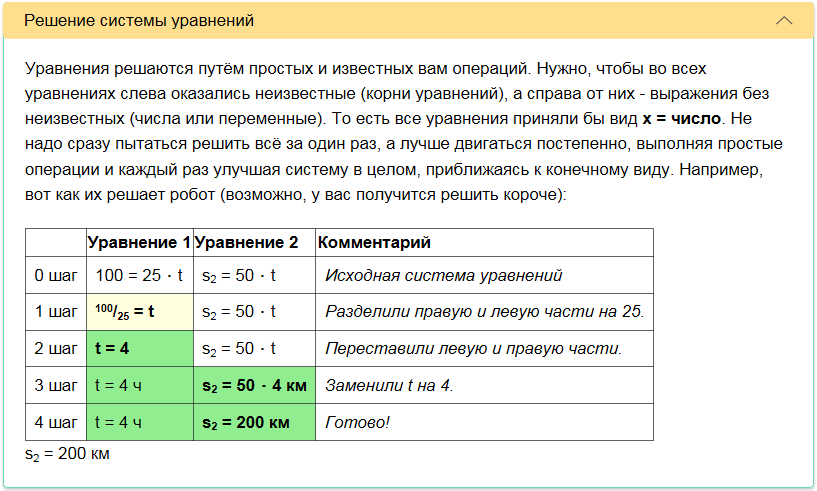
Der Roboter erkannte auch, dass es neben der universellen Methode eine Schullösungsmethode gibt, die kürzer und einfacher ist.



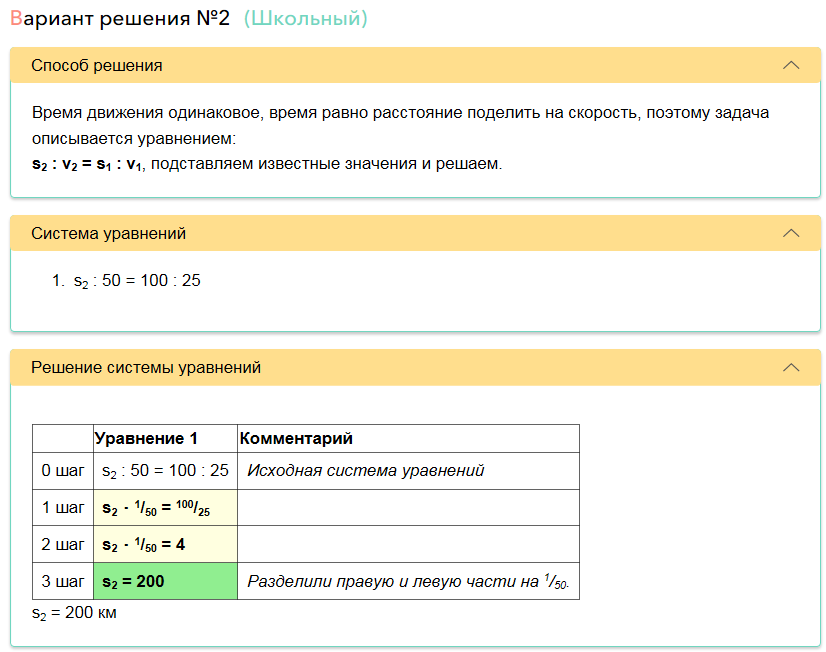
All dies zusammen mit dem Schema wird automatisch für jedes zu lösende Problem generiert und zunächst nicht festgelegt.

Der universelle Weg zu lösen

Die meisten Schultextprobleme können mit der universellen Methode gelöst werden - durch ein System einfacher Gleichungen. Wenn der Schüler diese Methode beherrscht, kann er im Prinzip jedes typische schulmathematische Problem lösen, das im Text angegeben ist.

In der 1. Klasse lernen Schulkinder, einfache Probleme zu lösen, die durch eine einzige Gleichung a = b + c oder a = b - c beschrieben werden. Und in der 3. Klasse treten nach Beherrschung der Multiplikationsoperationen mit Division einfache Probleme bei a = b ⋅ s oder a = b / c auf. Zusammengesetzte Probleme sind solche Probleme, die nicht einfach sind, dh nicht durch eine einzige Gleichung mit drei Größen beschrieben werden. Hier wird der Schüler aufgefordert, klug zu sein, um entweder eine komplexe Gleichung zu erstellen oder das Problem auf eine Reihe einfacherer Probleme zu reduzieren, die nacheinander gelöst werden. Compound- und Subtraktions-Composite-Aufgaben werden ab der 2. Klasse aktiv angeboten, und ab der 3. Klasse nimmt die Komplexität mit dem Aufkommen neuer Operationen noch mehr zu.

Es gibt aber auch eine andere Möglichkeit, zusammengesetzte Probleme zu lösen. Sie besteht darin, einige einfache Gleichungen (ein Gleichungssystem) zusammenzustellen und diese dann vollständig zu lösen. Wenn ein Schüler einfache Probleme lösen kann (dh eine einfache Gleichung gemäß dem Text der Bedingung korrekt zusammenstellen kann), kann er für ein zusammengesetztes Problem im Prinzip seine eigene einfache Gleichung für jede einzelne Bedingung erstellen. Dazu müssen alle vorkommenden Größen mit ihren Symbolen gekennzeichnet sein (z. B. x, y, z, ...) und für sie das entsprechende x = y + z usw. gebildet werden. Ersetzen Sie dann bestimmte Zahlen in der Gleichung. Und dann lösen Sie dieses System, indem Sie nacheinander unbekannte Werte bestimmen.

Diese Methode kann sich als zeitaufwändiger für die Lösung einer bestimmten Aufgabe herausstellen, da einige „Highlights“ normalerweise die Arbeit vereinfachen. Aber es kann nicht immer gefunden werden, da es eine Art Kunst ist. Eine universelle Methode erfordert dies nicht, da es sich um eine Technologie wie "einmal, dann zweimal, und hier ist die Antwort" handelt.

Der Roboter verwendet es auf universelle Weise und versucht, zu einer bestimmten Aufgabe so detailliert wie möglich zu erklären, wie er zu einer Lösung kommt. Es wird davon ausgegangen, dass der Schüler einige Zeit damit verbringen wird, zu verstehen, wie der Roboter dies tut, um ähnliche Aktionen in Zukunft bei anderen Aufgaben zu wiederholen. Der Roboter bietet jedoch auch eine Schullösung, wenn der Roboter für diese Art von Aufgabe darauf trainiert ist ( jetzt nicht für alle Typen, sondern nach und nach lernt ).

Es ist nützlich oder nicht für Studenten - ein strittiger Punkt. Dies kann zum einen den Prozentsatz der von den Schülern gelösten Aufgaben erhöhen. Auf der anderen Seite kann eine solche Technologie bei einigen Studenten die heiklen Triebe mathematischer Kenntnisse unterdrücken. Ich schlage vor, an den Autor zu senden oder meine vernünftigen Überlegungen und Bedenken hier aufzuschreiben.

Aufgabenklassifizierer

Nach einem System einfacher Gleichungen können Probleme automatisch klassifiziert werden. Dies kann zum Beispiel nützlich sein, um dem Schüler anzubieten, ein ähnliches Problem zu lösen, um die Fähigkeit zu festigen. Der Roboter kann auch verstehen, zu welcher Klasse die Aufgabe gehört, denn selbst in den Lehrbüchern der 4. Klasse gibt es Probleme mit dem Niveau der 1. Klasse!

Derzeit hat die Site mehr als 4000 Aufgaben aus echten Lehrbüchern heruntergeladen, und Sie können diesen automatischen Klassifikator für diese Aufgaben sehen.

Roboterimplementierung

Natürlich stellt sich eine vernünftige Frage: Wie macht dieser Roboter das? Ich muss sagen, dass dies eine sehr komplexe Implementierung ist. Ich verarbeite seit ungefähr 10 Jahren Texte in natürlicher Sprache , und dies ist die schwierigste Aufgabe, der ich in diesem Bereich begegnet bin. Die Schwierigkeit liegt in der Tatsache, dass Sie numerische Größen korrekt auswählen, ihren Typ verstehen und sich auf Objekte beziehen müssen. Jede Ungenauigkeit in mindestens einem Aspekt führt zu einem falschen Ergebnis.
Ich werde nur einige der Probleme auflisten, mit denen ich konfrontiert war.

• Pseudo-Mengen, die für das Problem nicht relevant sind (Es gab 2 blühende Rosen am Busch. Nach 3 Tagen blühten 4 weitere Rosen. Wie viele Rosen sind am Busch?);
• Implizite Werte, die durch verschiedene Kombinationen vom Typ "gleich", "halb von" usw. angegeben werden;
• Synonymie, wenn dasselbe Objekt durch verschiedene Kombinationen angezeigt wird (LKW = LKW);
• Schwierigkeiten bei der Identifizierung von Objekten (Motorschiffe fuhren von zwei Yachthäfen aufeinander zu ... - es ist nicht klar, wer die Objekte hier sind, Yachthäfen oder Motorschiffe?);
• Anaphora (Pronomen er, sie, es) bezieht sich nicht immer eindeutig auf ein Objekt;
• Die Notwendigkeit, die Aufgabe in Unteraufgaben aufzuteilen, wenn die Grundbedingung eins ist, aber zusätzliche Bedingungen oder was gefunden werden muss, variieren;
• Eine implizite Bedingung, die die Bedeutung der Aufgabe grundlegend ändert (Die Tischdecke hat 3 Winkel. Eine Ecke wurde geschnitten. Wie viele Ecken hatte die Tischdecke?);

Aber genau das liegt an der Oberfläche. Auf algorithmischer Ebene sind diese Probleme viel größer.
Die Hauptidee des Algorithmus besteht darin, dass bestimmte Task-Handler implementiert werden, die ihre Typen verstehen. Die Aufgabe wird von allen Handlern ausgeführt, und welcher erkennt ihren Typ, der das Problem löst. Jeder Handler löst eine ziemlich breite Palette von Aufgaben seiner Art.

Nun sind diese Typen:

• Aufgaben für die Bewegung eines oder mehrerer Objekte;
• Aufgaben auf Rechtecken und Quadraten (einem oder mehreren), Flächen, Umfängen, die sich gegenseitig füllen;
• Aufgaben für homogene Größen (wenn alle Größen auf eine Dimension reduziert sind und die Aufgabe selbst ein System linearer Gleichungen ist);
• Aufgaben für Größen von zwei Gattungen (wenn im Gleichungssystem eine Multiplikation vorhanden ist);
• Explizite Beschreibung der Gleichung (zum Beispiel ist der Quotient der Zahlen 2082 und 6 gleich der Summe der beabsichtigten Zahl und der Zahl 48);
• Aufgaben für die Tageszeit;
• Aufgaben im Durchschnitt, Transformation von Dimensionen und anderen Kleinigkeiten;

Wenn der Roboter die Aufgabe verstanden hat, dh sie einem der unterstützten Typen zugeordnet hat, nachdem er die Werte richtig eingestellt und verstanden hat, was berechnet werden muss, kann er sein Verständnis mit seiner eigenen Sprache erzeugen. Auf der Website wird dieses Verständnis übrigens rechts neben dem Text der Aufgaben für Lehrbücher angezeigt. Wir geben Beispiele von der Website.

Bedingung : Der Quotient der Zahlen 2082 und 6 ist gleich der Summe der beabsichtigten Zahl und der Zahl 48.
Verständnis : Finden Sie die Wurzel der Gleichung: 2082: 6 = x + 48.

Bedingung : Das Spiel für Kinder begann um 11 Uhr und endete um 12 Uhr 35 Minuten. Wie lange hat diese Aufführung gedauert?
Verständnis : Es gibt ein Zeitintervall. Der Beginn des Intervalls beträgt 11 Stunden. Das Ende des Intervalls beträgt 12 Stunden 35 Minuten. Wie lang ist das Intervall?

Zustand : Ane ist 12 Jahre alt. Sie ist dreimal älter als ihr Bruder. Wie alt ist Anya älter als ihr Bruder?
Verständnis : Es gibt 2 Zahlenwerte: Anis Alter und das Alter des Bruders. Ani ist 12 Jahre alt, er ist dreimal so alt wie sein Bruder. Wie viel älter ist Ani als ihr Bruder?

Zustand : Ein Wender macht 8 Teile pro Stunde und ein anderer - 7 Teile. Wie viele Stunden werden sie zusammen 90 Teile produzieren, wenn sich ihre Leistung pro Stunde nicht ändert?
Verständnis : Es gibt 2 Objekte: Turner Nr. 1 und Turner Nr. 2. Die Anzahl der Teile in Stunden des Wenders Nr. 1: 8 Teile. Die Anzahl der Teile in Stunden des Wenders Nr. 2: 7 Teile. Die Gesamtzahl der Teile zusammen: 90 Teile. Alle Objekte haben die gleiche Zeit. Was bedeutet Zeit in Stunden?

Zustand : Zwei Kameraden, Mischa und Kolya, kamen gleichzeitig aus zwei Dörfern aufeinander zu. Mischa ging mit einer Geschwindigkeit von 3 km / h und Kolya mit 5 km / h. Zur gleichen Zeit wie Mischa rannte ein Hund nach Kolya. Sie lief mit einer Geschwindigkeit von 8 km / h. Als sie Kolya erreichte, wandte sie sich wieder Mischa zu und rannte zwischen den Jungs hin und her, bis sie sich trafen. Wie viele Kilometer ist der Hund gelaufen, wenn die Entfernung zwischen den Dörfern 16 km beträgt?
Verständnis : Zwei Objekte (Mischa und Kolya) bewegten sich gleichzeitig aus einer Entfernung von 16 km aufeinander zu. Zwischen ihnen bewegt sich das dritte Objekt (Hund) mit einer Geschwindigkeit von 8 km / h hin und her. Das erste Objekt (Mischa) bewegte sich mit einer Geschwindigkeit von 3 km / h. Das zweite Objekt (Rad) bewegte sich mit einer Geschwindigkeit von 5 km / h. Welchen Weg in km hat das 3. Objekt überwunden?

Zustand : In dem Raum, dessen Länge 8 m beträgt und dessen Breite 2 m unter der Länge liegt, muss der Boden gestrichen werden. Wie viel Farbe benötigen Sie, wenn Sie 150 g pro 1 m2 ausgeben?
Verständnis : Ein Rechteck von 8 m Länge. Breite 2 m kleiner als Länge. Die Fläche ist mit Elementen von 150 g pro Flächeneinheit gefüllt. Wie viele Elemente befinden sich auf der gesamten Fläche?

Was weiter?

Folgende Entwicklungsrichtungen sind geplant:

• Erhöhen Sie den Prozentsatz der Aufgaben. Für Aufgaben der 4. Klasse zeigt der Roboter 65% der richtigen Lösungen, für die 3. Klasse - etwa 80% für 1 und 2 - ist der Prozentsatz sogar noch höher.
• Website-Werbung organisieren;
• Einführung in die Aufgaben aller gängigen Lehrbücher in Mathematik, auch für die GUS-Länder (auf Russisch);
• Unterstützung anderer Sprachen der slawischen Gruppe;
• Gehe in Richtung 5. Klasse und weiter;
• Denken Sie an Textprobleme in der Physik.

Die Implementierung dieser Bereiche hängt von der tatsächlichen Relevanz des Standorts ab.