In dem Artikel werden die Erfahrungen bei der Entwicklung eines Programms zur Schaffung eines effektiven Anleihenportfolios im Hinblick auf die Minimierung seiner Laufzeit erörtert . Vielleicht bin ich nicht originell und für alle, die in Anleihen investieren, sind die Probleme bei der Bestimmung der optimalen Gewichte längst gelöst. Dennoch hoffe ich, dass der beschriebene Ansatz und der bereitgestellte Programmcode für jemanden nützlich sind.

Der Artikel mag aufgrund des Vorhandenseins einer kleinen Menge Mathematik für jemanden kompliziert erscheinen. Wenn Sie sich jedoch bereits für eine Investition entschieden haben, müssen Sie darauf vorbereitet sein, dass Mathematik häufig in der finanziellen Realität zu finden ist und noch komplizierter ist.

Der Quellcode des Programms und ein Beispielportfolio zur Optimierung sind auf GitHub verfügbar .

UPDATE: Wie versprochen wurde ein einfacher Webdienst erstellt, der das Programm allen zur Verfügung stellt, ohne Code zu kopieren oder zu kompilieren.
der Link
Gebrauchsanweisung am selben Ort.
Wenn etwas nicht funktioniert oder Sie etwas reparieren müssen, schreiben Sie in die Kommentare.

Wir haben also die Aufgabe, ein effektives Portfolio von Anleihen aufzubauen.

Teil 1. Bestimmung der Duration des Portfolios

Unter dem Gesichtspunkt der Minimierung nicht systemischer Risiken (für die das Portfolio diversifiziert ist) wurde die Auswahl der Wertpapiere unter Berücksichtigung der Parameter einer bestimmten Emission, eines Emittenten (wenn nicht auf OFZ beschränkt), eines Papierverhaltens usw. durchgeführt. (Ansätze für eine solche Analyse sind für jeden Anleger recht individuell und werden in diesem Artikel nicht berücksichtigt).

Nachdem Sie mehrere Wertpapiere ausgewählt haben, die für eine Anlage am besten geeignet sind, stellt sich natürlich die Frage: Wie viele Anleihen jeder Emission müssen Sie kaufen? Dies ist die Aufgabe, das Portfolio so zu optimieren, dass die Risiken des Portfolios minimal sind.

Es ist natürlich, die Dauer als optimierten Parameter zu betrachten. Daher besteht die Aufgabe darin, das Gewicht der Wertpapiere im Portfolio so zu bestimmen, dass die Laufzeit des Portfolios für einige feste Portfoliorenditen minimal wäre. Hier müssen Sie einige Reservierungen vornehmen:

1. Die Laufzeit des Anleihenportfolios wird durch seine Wertpapiere bestimmt. Diese Dauer ist bekannt (sie ist gemeinfrei). Die Portfoliodauer entspricht nicht der maximalen Duration der darin enthaltenen Wertpapiere (es liegt ein solcher Irrtum vor). Die Beziehung zwischen der Laufzeit einzelner Wertpapiere und der Laufzeit des gesamten Portfolios ist nicht linear, d.h. ist nicht gleich der gewichteten durchschnittlichen Duration seiner konstituierenden Bindungen (Um dies zu überprüfen, reicht es aus, die Durationsformel (siehe (1) unten) zu berücksichtigen und zu versuchen, die gewichtete durchschnittliche Duration eines bedingten Portfolios zu berechnen, das beispielsweise aus zwei Papieren besteht. Ersetzen Sie die Formel für die Duration durch einen solchen Ausdruck Von jedem Papier erhalten wir bei der Ausgabe keine Formel für die Dauer des Portfolios, sondern eine Art "Unsinn" mit zwei Abzinsungssätzen und inkonsistenten Cashflows als Gewichtung.
2. Im Gegensatz zur Duration hängt die Portfoliorendite linear von den Renditen der darin enthaltenen Instrumente ab. Das heißt, Wenn wir Geld in mehrere Instrumente mit festem Einkommen investieren, erhalten wir eine Rendite, die direkt proportional zum Investitionsvolumen in jedes Instrument ist (und dies funktioniert für einen komplexen Zinssatz und nicht nur für einen einfachen). Stellen Sie sicher, dass dies noch einfacher ist.
3. Die Rendite bis zur Fälligkeit ( YTM ) wird als Anleiherendite verwendet. Es wird normalerweise zur Berechnung der Dauer verwendet. Die Rendite bis zur Fälligkeit des gesamten Portfolios ist hier jedoch eher willkürlich Die Laufzeit aller Wertpapiere ist unterschiedlich. Bei der Bildung eines Portfolios muss dieses Merkmal in dem Sinne berücksichtigt werden, dass das Portfolio überprüft werden sollte, und nicht weniger als die Tools, aus denen es besteht, aus dem Verkehr gezogen werden.

Die erste Aufgabe ist also die korrekte Berechnung der Laufzeit des Portfolios. Der unmittelbare Weg dazu besteht darin , alle Zahlungen für das Portfolio zu ermitteln, die Rendite bis zur Fälligkeit zu berechnen, die Zahlungen abzuzinsen, die erhaltenen Werte mit den Bedingungen dieser Zahlungen zu multiplizieren und zu addieren. Dazu müssen Sie die Zahlungskalender aller Instrumente in einem einzigen Zahlungskalender für das gesamte Portfolio zusammenfassen, einen Ausdruck für die Berechnung der Rendite bis zur Fälligkeit erstellen, diese berechnen, für jede Zahlung diskontieren, mit dem Fälligkeitsdatum multiplizieren, hinzufügen ... Im Allgemeinen ein Albtraum. Dies auch für zwei Papiere zu tun, ist eine sehr mühsame Aufgabe, ganz zu schweigen von einer regelmäßigen Neuberechnung des Portfolios in der Zukunft. Dieser Weg passt nicht zu uns.

Daher muss nach einer Möglichkeit gesucht werden, die Duration des Portfolios auf andere, schnellere Weise zu bestimmen. Eine akzeptable Option wäre eine, mit der Sie die Duration des Portfolios anhand bekannter Instrumentendauern bestimmen können. Studien der Dauerformel haben gezeigt, dass es einen solchen Pfad gibt, und hier möchte ich ihn ausführlich beschreiben (wenn jemand nicht an den mathematischen Details der Berechnungen interessiert ist, können Sie sicher einige Absätze mit den Formeln überspringen und direkt zum Beispiel gehen).

Die Laufzeit eines Schuldtitels ist wie folgt definiert:

$$$$ display $$ \ begin {Gleichung} D = \ frac {\ sum_ {i} PV_i \ cdot t_i} {\ sum_ {i} PV_i} ~~~~~~~~~~~~~ (1) \ Ende {Gleichung} $$ Anzeige $$

wo:

• t _i ist der Zeitpunkt der i-ten Zahlung;
• $$$ inline $ \ begin {Gleichung} PV_i = \ frac {CF_i} {(1 + r) ^ {t_i}} \ end {Gleichung} $ inline $ - i-te ermäßigte Zahlung;
• CF _i - i-te Zahlung;
• r ist der Abzinsungssatz.

Wir führen den Abzinsungskoeffizienten k = (1 + r) ein und betrachten die Höhe der abgezinsten Zahlungen P als Funktion von k :

$$$$ display $$ \ begin {Gleichung} P (k) = \ sum_ {i} PV_i = \ sum_ {i} {\ frac {CF_i} {k ^ {t_i}}} ~~~~~~~~~~ ~~~~ (2) \ end {Gleichung} $$ Anzeige $$

Wenn wir P in Bezug auf k differenzieren , erhalten wir

$$$$ display $$ \ begin {Gleichung} P '(k) = - \ sum_ {i} {t_i \ frac {CF_i} {k ^ {t_i + 1}}} = - \ frac {1} {k} \ sum_ {i} {t_i \ frac {CF_i} {k ^ {t_i}}} ~~~~~~~~~~~~~ (3) \ end {Gleichung} $$ display $$

In letzterem Fall hat der Ausdruck für die Dauer der Bindung die Form

$$$$ display $$ \ begin {Gleichung} D = -k \ frac {P '(k)} {P (k)} ~~~~~~~~~~~~~ (4) \ end {Gleichung} $$ Anzeige $$

Gleichzeitig erinnern wir daran, dass als Abzinsungssatz r im Fall einer Anleihe die Rendite bis zur Fälligkeit (YTM) verwendet wird.

Der erhaltene Ausdruck gilt für eine Anleihe, wir sind jedoch an einem Portfolio von Anleihen interessiert. Fahren wir mit der Bestimmung der Duration des Portfolios fort.

Wir führen die folgende Notation ein:

• P _i ist der Preis der i-ten Anleihe;
• z _i - die Anzahl der Wertpapiere der i-ten Anleihe im Portfolio;
• k _i - Abzinsungskoeffizient der i-ten Anleihe im Portfolio;
• $$$ inline $ \ begin {Gleichung} P_p = \ sum_ {i} {z_iP_i} \ end {Gleichung} $ inline $ - Portfoliopreis;
• $$$ inline $ \ begin {Gleichung} w_i = \ frac {z_iP_i} {\ sum_ {i} z_iP_i} = \ frac {z_iP_i} {P_p} \ end {Gleichung} $ inline $ - das Gewicht der i-ten Anleihe im Portfolio; offensichtliche Anforderung$$ $ inline $ \ begin {Gleichung} \ sum_ {i} w_i = 1 \ end {Gleichung} $ inline $ ;;
• $$$ inline $ \ begin {Gleichung} k_p = \ sum_ {i} w_ik_i \ end {Gleichung} $ inline $ - Portfolio-Abzinsungskoeffizient;

Aufgrund der Linearität der Differenzierung gilt Folgendes:

$$$$ Anzeige $$ \ begin {Gleichung} P'_p (k) = \ left (\ sum_ {i} z_iP_i (k) \ right) '= \ sum_ {i} z_iP'_i (k) ~~~~~ ~~~~~~~~~ (5) \ end {Gleichung} $$ Anzeige $$

Unter Berücksichtigung von (4) und (5) kann die Duration des Portfolios also ausgedrückt werden als

$$$$ display $$ \ begin {Gleichung} D_p = -k_p \ frac {P'_p} {P_p} = - \ sum_ {i} w_ik_i \ left (\ frac {\ sum_ {j} z_jP'_j} {\ sum_ {j} z_jP_j} \ right) ~~~~~~~~~~~~~~ (6) \ end {Gleichung} $$ display $$

Aus (4) folgt eindeutig$$ $ inline $ \ begin {Gleichung} P'_j = - \ frac {D_jP_j} {k_j} \ end {Gleichung} $ inline $ .
Wenn wir diesen Ausdruck in (6) einsetzen, erhalten wir die folgende Formel für die Portfoliodauer:

$$$$ display $$ \ begin {Gleichung} D_p = \ sum_ {i} w_ik_i \ left (\ frac {\ sum_ {j} \ frac {D_j} {k_j} z_jP_j} {\ sum_ {j} z_jP_j} \ right) = \ left (\ sum_ {i} w_ik_i \ right) \ left (\ sum_ {j} w_j \ frac {D_j} {k_j} \ right) ~~~~~~~~~~~~~~ (7) \ Ende {Gleichung} $$ Anzeige $$

Unter den Bedingungen, unter denen die Duration und die Rendite bis zur Fälligkeit jedes Instruments bekannt sind (und wir erinnern uns, dass wir uns in genau diesen Bedingungen befinden), ist Ausdruck (7) die gewünschte Formel zur Bestimmung der Duration eines Portfolios basierend auf der Duration seiner Anleihen. Es sieht nur kompliziert aus, ist aber bereits mit Hilfe der einfachsten Funktionen von MS Excel für den praktischen Gebrauch bereit, was wir nun anhand eines Beispiels tun werden.

Beispiel

Um die Duration des Portfolios gemäß Formel (7) zu berechnen, benötigen wir Eingabedaten, die den tatsächlichen Satz der im Portfolio enthaltenen Wertpapiere, deren Duration und Rendite bis zur Fälligkeit enthalten. Wie oben erwähnt, sind diese Informationen beispielsweise auf der Website rusbonds.ru im Abschnitt Analyse von Anleihen öffentlich verfügbar. Quelldaten können im Excel-Format heruntergeladen werden.

Betrachten Sie als Beispiel ein Wertpapierportfolio, das aus 9 Anleihen besteht. Die von rusbonds heruntergeladene Originaldatentabelle hat das folgende Formular.



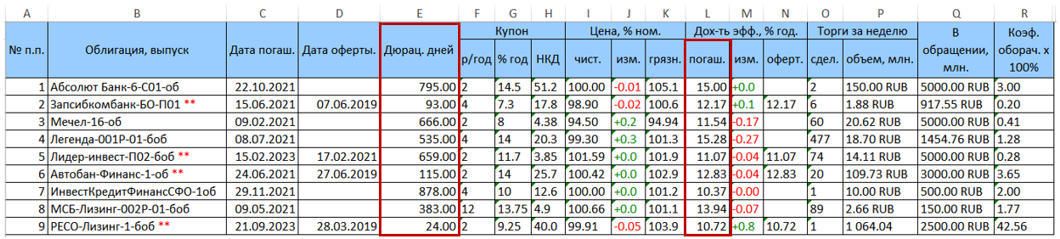
Zwei für uns interessante Spalten mit einer Duration (Spalte E) und einer Rendite bis zur Fälligkeit (Spalte L = YTM) sind rot hervorgehoben.

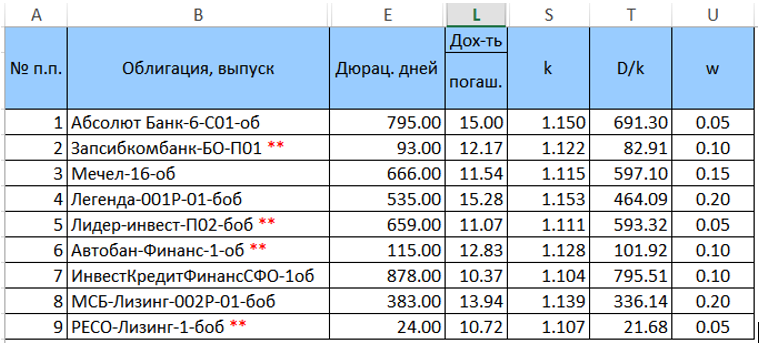
Wir setzen Gewichte w für Anleihen in diesem Portfolio (bisher willkürlich, aber so, dass ihre Summe gleich Eins ist) und berechnen k = (1 + YTM / 100) und D / k = („Spalte E“ / k). Die konvertierte Tabelle (ohne zusätzliche Spalten) sieht folgendermaßen aus



Als nächstes berechnen wir das Produkt$$ $ inline $ \ begin {Gleichung} w_j \ frac {D_j} {k_j} \ end {Gleichung} $ inline $ und$$ $ inline $ \ begin {Gleichung} w_ik_i \ end {Gleichung} $ inline $ und summiere sie und multipliziere die resultierenden Beträge miteinander. Das Ergebnis dieser Multiplikation ist die gewünschte Dauer für eine gegebene Gewichtsverteilung.



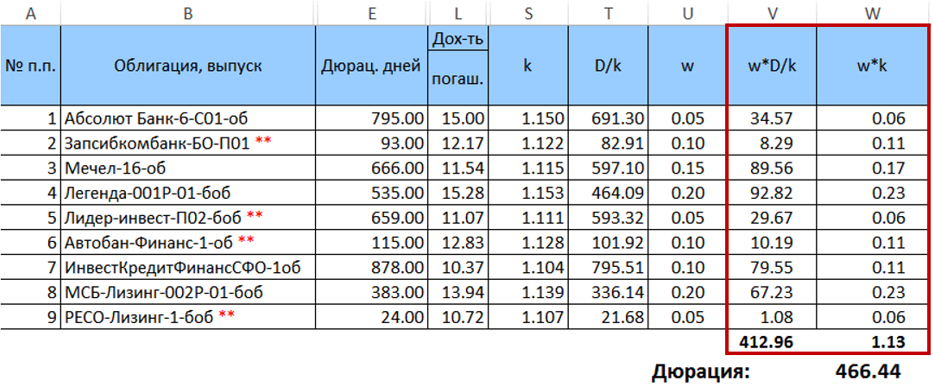
Die gewünschte Laufzeit des Portfolios beträgt also 466,44 Tage. Es ist wichtig zu beachten, dass in diesem speziellen Fall die nach Formel (7) berechnete Dauer geringfügig von der mit denselben Gewichten berechneten gewichteten durchschnittlichen Dauer abweicht (Abweichung <0,5 Tage). Dieser Unterschied nimmt jedoch mit zunehmender Streuung der Gewichte zu. Sie wird auch mit zunehmender Verbreitung der Papierdauer zunehmen.

Nachdem wir die Formel zur Berechnung der Duration des Portfolios erhalten haben, besteht der nächste Schritt darin, das Gewicht der Wertpapiere so zu bestimmen, dass bei einer bestimmten Rendite die geschätzte Duration des Portfolios minimal ist. Wir fahren mit dem nächsten Teil fort - der Portfoliooptimierung.

Teil 2. Optimierung des Anleihenportfolios

Ausdruck (7) ist eine quadratische Form mit der Matrix

$$$$ display $$ \ begin {Gleichung} A = \ left \ {k_i \ frac {D_j} {k_j} \ right \} = \ begin {pmatrix} D_1 & \ ldots & k_1 \ frac {D_n} {k_n} \ \ \ vdots & D_j & \ vdots \\ k_n \ frac {D_1} {k_1} & \ ldots & D_n \ end {pmatrix} \ end {Gleichung} $$ display $$

Dementsprechend kann in Matrixform der Ausdruck für die Dauer des Portfolios (7) wie folgt geschrieben werden:

$$$$ Anzeige $$ \ begin {Gleichung} D_p = w ^ TAw ~~~~~~~~~~~~~~ (8) \ end {Gleichung} $$ Anzeige $$

Dabei ist w der Spaltenvektor der Anleihegewichte im Portfolio. Wie oben erwähnt, muss die Summe der Elemente des Vektors w gleich Eins sein. Auf der anderen Seite der Ausdruck $$$k_p = \ sum_ {i} w_i k_i$ (was im Wesentlichen ein einfaches Skalarprodukt ist ( w , k ) , wobei k der Vektor der Abzinsungskoeffizienten für Anleihen ist) sollte gleich dem Zielabzinsungssatz des Portfolios sein, und daher sollte die Zielportfoliorendite festgelegt werden.

Die Aufgabe der Optimierung eines Anleihenportfolios besteht daher darin, die quadratische Funktion (8) mit linearen Einschränkungen zu minimieren.

Die klassische Methode zum Auffinden des bedingten Extremums einer Funktion mehrerer Variablen ist die Lagrange-Multiplikatormethode. Diese Methode ist hier jedoch nicht anwendbar, schon allein deshalb, weil die Matrix A konstruktionsbedingt entartet ist (aber nicht nur aus diesem Grund; wir lassen die Details der Analyse der Anwendbarkeit der Lagrange-Methode hier weg, um den Artikel nicht mit übermäßigem mathematischen Inhalt zu überladen).

Die Unfähigkeit, eine einfache und kostengünstige Analysemethode anzuwenden, führt dazu, dass numerische Methoden verwendet werden müssen. Das Problem der Optimierung einer quadratischen Funktion ist bekannt und verfügt über mehrere lange entwickelte effiziente Algorithmen, die in öffentlichen Bibliotheken implementiert sind.

Um dieses spezielle Problem zu lösen, wurden die ALGLIB-Bibliothek und die darin implementierten quadratischen Optimierungsalgorithmen QP-Solvers verwendet , die im minqp-Paket enthalten sind.

Das quadratische Optimierungsproblem ist im Allgemeinen wie folgt:

Es ist erforderlich, einen n-dimensionalen Vektor w zu finden, der die Funktion minimiert

$$$$ display $$ \ begin {Gleichung} F = \ frac {1} {2} w ^ T Qw + b ^ T w ~~~~~~~~~~~~~ (9) \ end {Gleichung} $$ Anzeige $$

Mit vorgegebenen Einschränkungen
1) l ≤ w ≤ u ;
2) Cw * d ;
wobei w, l, u, d, b n-dimensionale reelle Vektoren sind, Q die symmetrische Matrix des quadratischen Teils ist und das Vorzeichen * eine der Beziehungen ≥ = ≤ bedeutet.
Wie aus (8) ersichtlich ist, ist der lineare Teil b ^T w in unserer Zielfunktion gleich Null. Die Matrix A ist jedoch nicht symmetrisch, was jedoch nicht verhindert, dass sie in eine symmetrische Form gebracht wird, ohne die Funktion selbst zu ändern. Geben Sie dazu anstelle von A den Ausdruck ein$$ $ inline $ \ begin {Gleichung} \ frac {A ^ T + A} {2} \ end {Gleichung} $ inline $ Da Formel (9) den Koeffizienten enthält $$$\ frac {1} {2}$ dann können wir als Q akzeptieren $$$A ^ T + A$ .

Die Koordinaten der Vektoren l und u geben die Grenzen des gewünschten Vektors an und liegen im Bereich [-1,1]. Da wir keine Leerverkäufe von Anleihen annehmen, sind die Koordinaten der Vektoren in unserem Fall alle nicht kleiner als 0. Im folgenden Beispielprogramm wird der Einfachheit halber angenommen, dass der Vektor l Null ist und die Koeffizienten des Vektors u alle 0,3 sind . Nichts hindert uns jedoch daran, das Programm zu verbessern und die Einschränkungsvektoren anpassbarer zu machen.

Matrix C besteht in unserem Fall aus zwei Zeilen: 1) Abzinsungskoeffizienten, die, wenn sie skalar mit Gewichten multipliziert werden (gleich ( w , k )), die Zielrendite für das Portfolio ergeben sollten; 2) eine Zeichenfolge, die aus Einheiten besteht. Es ist erforderlich, Grenzen zu setzen $$$\ sum_ {i} w_i = 1$ .

Der Ausdruck Cw * d für unsere Aufgabe sieht also folgendermaßen aus:

$$$$ display $$ \ begin {Gleichung} \ left \ {\ begin {array} {ccc} ({\ bf w, k}) = k_p \\ \ sum_ {i} w_i = 1 \\ \ end {array} \ richtig. ~~~~~~~~~~~~~ (10) \ end {Gleichung} $$ display $$

Wir wenden uns nun der Software-Implementierung der Suche nach dem optimalen Portfolio zu. Die Basis des quadratischen Optimierers in ALGLIB ist das Objekt $$$\ tt \ small minqpstate$

alglib::minqpstate state; 

Um das Optimierungsprogramm zu initialisieren, wird dieses Objekt zusammen mit dem Taskdimensionsparameter n an die Funktion minqpcreate übergeben

 alglib::minqpcreate(n, state); 

Der nächstwichtigste Punkt ist die Wahl des Optimierungsalgorithmus (Solver). Die ALGLIB-Bibliothek zur quadratischen Optimierung bietet drei Löser:

• QP-BLEIC ist der universellste Algorithmus zur Lösung von Problemen mit einer nicht sehr großen Anzahl (bis zu 50 gemäß den Empfehlungen der Dokumentation) linearer Einschränkungen (in der Form Cw * d ). Gleichzeitig kann es bei Aufgaben mit großer Dimension wirksam sein (wie in der Dokumentation angegeben - bis zu n = 10000).
• QuickQP ist ein sehr effizienter Algorithmus, insbesondere wenn eine konvexe Funktion optimiert ist. Leider kann es nicht mit linearen Randbedingungen arbeiten - nur mit Randbedingungen (der Form l ≤ w ≤ u ).
• Dense-AUL - optimiert für den Fall sehr großer Abmessungen und einer Vielzahl von Einschränkungen. Der Dokumentation zufolge werden Aufgaben mit kleinen Abmessungen und die Anzahl der Einschränkungen mithilfe anderer Algorithmen effizienter gelöst.

Angesichts der oben genannten Eigenschaften ist es offensichtlich, dass der QP-BLEIC-Solver für unsere Aufgabe am besten geeignet ist.

Um den Optimierer anzuweisen, diesen Algorithmus zu verwenden, müssen Sie die Funktion aufrufen $$$\ tt \ small minqpsetalgobleic$ . Das Objekt selbst und die Stoppkriterien werden an diese Funktion übergeben, auf die wir nicht näher eingehen werden: In dem hier betrachteten Programm werden die Standardwerte verwendet. Der Funktionsaufruf lautet wie folgt:

 alglib::minqpsetalgobleic(state, 0.0, 0.0, 0.0, 0); 

Weitere Initialisierung des Lösers umfasst:

• Die Übertragung der Matrix des quadratischen Teils Q - $$$\ tt \ small alglib :: minqpsetquadraticterm (state, qpma);$
• Die Übertragung des Vektors des linearen Teils (in unserem Fall des Nullvektors) - $$$\ tt \ small alglib :: minqpsetlinearterm (state, b);$
• Die Übertragung der Randbedingungsvektoren l und u - $$$\ tt \ small alglib :: minqpsetbc (state, bndl, bndu);$
• Lineargetriebe - $$$\ tt \ small alglib :: minqpsetlc (state, c, ct);$
• Einstellen der Koordinatenskala des Vektorraums $$$\ tt \ small alglib :: minqpsetscale (state, s);$

Lassen Sie uns auf jeden Punkt eingehen:
Um Vektoren und Matrizen anzugeben, verwendet die ALGLIB-Bibliothek Objekte spezieller Typen (ganzzahlig und reellwertig): $$$\ tt \ small alglib :: integer \ _1d \ _array$ , $$$\ tt \ small alglib :: real \ _1d \ _array$ , $$$\ tt \ small alglib :: integer \ _2d \ _array$ , $$$\ tt \ small alglib :: real \ _2d \ _array$ . Um die Matrix vorzubereiten, benötigen wir einen Typ $$$\ tt \ small real \ _2d \ _array$ . Erstellen Sie im Programm zunächst eine Matrix A ( $$$\ tt \ small alglib :: real \ _2d \ _array ~ qpma$ ) und dann nach der Formel $$$Q = A ^ T + A$ daraus konstruieren wir die Matrix Q ( $$$\ tt \ small alglib :: real \ _2d \ _array ~ qpmq$ ) Das Festlegen von Matrixdimensionen in ALGLIB ist eine separate Funktion $$$\ tt \ kleine Solllänge (n, m)$ .

Um die Matrizen zu konstruieren, benötigen wir den Vektor der Abzinsungskoeffizienten ( k _i ) und das Verhältnis der Dauer zu diesen Koeffizienten ( $$$\ frac {D_j} {k_j}$ ):

 std::vector<float> disfactor; std::vector<float> durperytm; 

Das Code-Snippet, das die Konstruktion von Matrizen implementiert, wird in der folgenden Liste gezeigt:

 size_t n = durations.size(); alglib::real_2d_array qpma; qpma.setlength(n,n); // matrix nxn alglib::real_2d_array qpmq; qpmq.setlength(n,n); // matrix nxn for(size_t j=0; j < n; j++) { for (size_t i = 0; i < n; i++) qpma(i,j) = durperytm[j]*disfactor[i]; //i,j   } for(size_t j=0; j < n; j++) { for (size_t i = 0; i < n; i++) qpmq(i,j) = qpma(i,j) + qpma(j,i); } 

Der Vektor des linearen Teils ist in unserem Fall, wie bereits angegeben, Null, daher ist damit alles einfach:

 alglib::real_1d_array b; b.setlength(n); for (size_t i = 0; i < n; i++) b[i] = 0; 

Vektorgrenzbedingungen werden von einer Funktion übertragen. Um dieses Problem zu lösen, werden sehr einfache Randbedingungen angewendet: Das Gewicht jedes Papiers sollte nicht kleiner als Null sein (wir erlauben keine negativen Positionen) und 30% nicht überschreiten. Falls gewünscht, können die Einschränkungen kompliziert sein. Experimente mit dem Programm haben gezeigt, dass bereits eine einfache Änderung dieses Bereichs die Ergebnisse stark beeinflussen kann. Eine Erhöhung der unteren Grenze und / oder eine Verringerung der oberen Grenze führt daher zu einer stärkeren Diversifizierung des endgültigen Portfolios, da ein Löser während der Optimierung einige Wertpapiere aus dem resultierenden Vektor ausschließen kann (ihnen ein Gewicht von 0% zuweisen), da sie nicht geeignet sind. Wenn Sie die Untergrenze der Skalen beispielsweise auf 5% festlegen, werden alle Papiere garantiert in das Portfolio aufgenommen. Die berechnete Dauer bei solchen Einstellungen ist jedoch natürlich größer als in dem Fall, in dem der Optimierer Papier ausschließen kann.

Die Randbedingungen werden also durch zwei Vektoren festgelegt und auf den Löser übertragen:

 alglib::real_1d_array bndl; bndl.setlength(n); for (size_t i = 0; i < n; i++) bndl[i] = 0.0; // low boundary alglib::real_1d_array bndu; bndu.setlength(n); for (size_t i = 0; i < n; i++) bndu[i] = 0.3;// high boundary alglib::minqpsetbc(state, bndl, bndu); 

Als nächstes muss der Optimierer die vom System (10) angegebenen linearen Einschränkungen übergeben. In ALGLIB erfolgt dies mit der Funktion $$$\ tt \ small alglib :: minqpsetlc (state, c, ct)$ wobei c die Matrix ist, die die linke und rechte Seite des Systems (10) kombiniert, d.h. Matrix anzeigen $$$(C ~~ d)$ und ct ist der Vektor von Beziehungen (d. h. Entsprechungen der Form ≥, = oder ≤). In unserem Fall ist ct = (0,0), was dem Verhältnis '=' für beide Systemzeilen (10) entspricht.

 for (size_t i = 0; i < n; i++) { c(0,i) = disfactor[i]; //   -    c(1,i) = 1; //   –  –    } c(0,n) = target_rate; //   ( ) –    c(1,n) = 1; //   ( ) –  ,   alglib::integer_1d_array ct = "[0,0]"; //   alglib::minqpsetlc(state, c, ct); 

In der Dokumentation zur ALGLIB-Bibliothek wird dringend empfohlen, die Skalierung der Variablen festzulegen, bevor Sie das Optimierungsprogramm starten. Dies ist besonders wichtig, wenn die Variablen in Einheiten gemessen werden, deren Änderung sich um Größenordnungen unterscheidet (beispielsweise können bei der Suche nach einer Lösung Tonnen in Hundertstel oder Tausendstel und Meter in Einheiten geändert werden; das Problem kann im Tonnen-Meter-Raum gelöst werden). was sich auf die Kriterien für die Aufgabe auswirkt. Es gibt jedoch einen Vorbehalt, dass bei gleicher Skalierung von Variablen das Einstellen der Skalierung nicht erforderlich ist. In dem betrachteten Programm führen wir immer noch die Aufgabe der Skalierung aus, um den Ansatz strenger zu gestalten, zumal dies sehr einfach ist.

 alglib::real_1d_array s; s.setlength(n); for (size_t i = 0; i < n; i++) s[i] = 1; //     alglib::minqpsetscale(state, s); 

Als nächstes setzen wir den Optimierer als Ausgangspunkt. Im Allgemeinen ist dieser Schritt auch optional, und das Programm bewältigt die Aufgabe erfolgreich ohne einen klar definierten Ausgangspunkt. In ähnlicher Weise legen wir aus Gründen der Strenge den Ausgangspunkt fest. Wir werden nicht schlau sein: Der Ausgangspunkt ist der Punkt mit den gleichen Gewichten für alle Anleihen.

 alglib::real_1d_array x0; x0.setlength(n); double sp = 1/n; for (size_t i = 0; i < n; i++) x0[i] = sp; alglib::minqpsetstartingpoint(state, x0); 

Es bleibt zu bestimmen, in welche Variable der Optimierer die gefundene Lösung und die Statusvariable zurückgibt. Anschließend können Sie die Optimierung ausführen und das Ergebnis verarbeiten

 alglib::real_1d_array x; //   alglib::minqpreport rep; //  alglib::minqpoptimize(state); //   alglib::minqpresults(state, x, rep); //      alglib::ae_int_t tt = rep.terminationtype; if (tt>=0) //       { std::cout << "   :" << '\n'; for(size_t i = 0; i < n; i++) //       { std::cout << (i+1) << ".\t" << bonds[i].bondname << ":\t\t\t " << (x(i)*100) << "\%" << std::endl; } for (size_t i = 0; i < n; i++) { for (size_t j = 0; j < n; j++) { qpmq(i,j) /= 2; } } } 

Insbesondere wurde die Laufzeit des Programms in den Experimenten nicht gemessen, aber alles funktioniert sehr schnell. Gleichzeitig ist klar, dass ein privater Investor ein Portfolio von mehr als 10-15 Anleihen wahrscheinlich nicht optimieren wird.

Es ist auch wichtig, Folgendes zu beachten. Der Optimierer gibt genau den Vektor der Gewichte zurück. Um die berechnete Dauer selbst zu erhalten, müssen Sie direkt die Formel (8) verwenden. Das Programm kann dies tun. Zu diesem Zweck wurden speziell zwei Funktionen zum Multiplizieren von Vektoren und Matrizen hinzugefügt. Wir werden sie hier nicht geben. Wer es sich wünscht, findet sie leicht in den veröffentlichten Quellcodes.

Das ist alles Eine effektive Investition in Schuldtitel für alle.

PS Da ich verstehe, dass das Auswählen des Codes eines anderen nicht der attraktivste Beruf ist und für viele Leute, die investieren möchten, überhaupt nicht spezialisiert ist, werde ich versuchen, dieses Programm etwas später in einen einfachen Webdienst umzuwandeln, den jeder nutzen kann, unabhängig von mathematischen Kenntnissen und Programmierung.