 Originalübersetzung in meinem Blog
Originalübersetzung in meinem BlogSteven Wolfram Live Contest Broadcast (auf Englisch) Website des WettbewerbsLassen Sie uns den Lesern erklären, was „Regel 30“ bedeutet - dies ist ein elementarer zellularer Automat (siehe Wiki ), dessen Zustand (die Regel zum Aufbau einer neuen Ebene von Zellen basierend auf der alten) im Binärzahlensystem als 0-0-0-1-1-1 festgelegt ist -1-0, was in Dezimalschreibweise als 30 interpretiert werden kann.
Wo hat alles angefangen? - "Regel 30"
Wie kann es sein, dass etwas
unglaublich Einfaches etwas unglaublich Komplexes hervorbringt ? Es ist fast 40 Jahre her, seit ich
Regel 30 kennengelernt habe, aber es überrascht mich immer noch und erfreut mich. Lange Zeit wurde es zu meiner persönlichen Lieblingsentdeckung in der
Geschichte der Wissenschaft. Im Laufe der Jahre hat es mein gesamtes Weltbild verändert und mich zu einer
Vielzahl neuer Arten des Verständnisses von Wissenschaft, Technologie, Philosophie und vielem mehr geführt .
Aber auch nach so vielen Jahren gibt es noch viele grundlegende Konzepte zu Regel 30, die für uns unzugänglich bleiben. Und so entschied ich, dass es Zeit war, alles zu tun, um den Prozess der Identifizierung der Grundmenge dieser Grundmuster anzuregen.
Daher biete ich Bewerbern heute 30.000 USD als Gesamtpreis für die Beantwortung der drei Hauptfragen zu Regel 30 an.
Regel 30 ist sehr einfach:
Es gibt eine Folge von Reihen von schwarzen und weißen Zellen (Zellen), und bei einer bestimmten Reihe von schwarzen und weißen Zellen werden die Farben der Zellen in der folgenden Zeile bestimmt, wobei jede Zelle einzeln und ihre benachbarten benachbarten Zellen betrachtet werden. Dann wird die folgende einfache Substitutionsregel auf sie angewendet, nämlich:

CodeRulePlot[CellularAutomaton[30]]
[Sehen Sie sich das Video an, das in wenigen Minuten die Essenz zellularer Automaten und Regel 30 - Anmerkung des Übersetzers - erklärt.]
Was passiert, wenn Sie mit einer schwarzen Zelle beginnen? [Eine
Reihe weißer Zellen wird genommen, unendlich auf beiden Seiten und eine schwarze Zelle, dann gelten die oben gezeigten Regeln für diese Reihe, eine neue Reihe wird erhalten usw. - Anmerkung des Übersetzers ] Nehmen wir an (wie ich es zuerst selbst getan habe) Die Regel ist recht einfach, und die Vorlage, die aufgrund ihrer Arbeit erhalten wird, sollte auch entsprechend einfach sein. Wenn Sie jedoch ein Experiment durchführen, werden Sie sehen, was nach den ersten 50 Schritten des Algorithmus passiert:

CodeRulePlot[CellularAutomaton[30], {{1}, 0}, 50, Mesh -> All,
ImageSize -> Full]
Natürlich können wir davon ausgehen, dass durch den Algorithmus ein viel einfacheres mathematisches Objekt erhalten wird. Nach den ersten 300 Schritten geschieht jedoch Folgendes:

Dies zeigt, dass es ein bestimmtes
Muster gibt - auf der linken Seite der Pyramide . Gleichzeitig sehen viele Aspekte dieser Vorlage
wie etwas aus, das zufällig erstellt wurde .
Es ist unverständlich, dass eine so einfache Regel letztendlich zu einem so komplexen Systemverhalten führen kann. Auf dieser Grundlage bin ich zu dem Schluss gekommen,
dass dieses Verhalten im Computeruniversum aller möglichen Computerprogramme weit verbreitet ist, noch mehr, fast überall.
Basierend auf dieser Hypothese entwickelte ich einen Ansatz zur Bildung einer völlig
neuen Art von Wissenschaft - basierend auf den
Prinzipien der Beobachtung der Funktionsweise einfacher Algorithmen.
Allmählich häuften sich mehr Beweise für diese Prinzipien.
Kehren wir jedoch zu Regel 30 zurück und überlegen wir uns im Detail, was genau es uns erlaubt und wozu es dient. Was genau kann über das Verhalten dieses Algorithmus gesagt werden? Es ist sofort ersichtlich, dass sich selbst die Antworten auf die offensichtlichsten Fragen als schwierig herausstellen.
Selbst nach Jahrzehnten, für die keine Antworten gefunden wurden, entschied ich, dass es Zeit war, einige spezifische Fragen zu Regel 30 zu stellen und diesen Bereich mit ernsthaften Geldpreisen anzuregen.
Ich habe bereits 2007 versucht, etwas Ähnliches zu tun,
indem ich
einen Preis für die Beantwortung der grundlegenden Frage zu einer bestimmten
Turing-Maschine festlegte . In diesem Fall war das Ergebnis positiv und das Warten dauerte nicht lange. Nur wenige Monate später wurde dieser
Preis gewonnen - nachdem er für immer festgestellt hatte, was die einfachste der möglichen universellen Turing-Maschinen ist, und auch das allgemeine
Prinzip der rechnerischen Äquivalenz , das ich zuvor persönlich entwickelt hatte, sehr überzeugend bewiesen hat.
Der Wettbewerb nach Regel 30 setzt sich erneut das Ziel, eine Schlüsselaufgabe zu lösen:
Wie komplex ist das Verhalten von Regel 30 ? Jede der Aufgaben wirft auf ihre Weise und spezifisch eine Frage in diesem Bereich auf. Wie Regel 30 selbst sind sie alle in ihrer ursprünglichen Einstellung täuschend einfach. Dennoch wird die Lösung für jeden von ihnen eine enorme Leistung sein, die letztendlich dazu beitragen wird, die Grundprinzipien der Eigenschaften der Bildung des Computeruniversums zu beleuchten, die weit über die Besonderheiten von Regel 30 hinausgehen.
Ich
arbeite seit über 35 Jahren an jedem dieser Themen . Und die ganze Zeit habe ich versucht, die richtige Idee im Rahmen eines konsistenten mathematischen oder rechnerischen Denkens zu finden, mit dem Ziel, mindestens eines dieser Probleme endgültig zu lösen. Jetzt möchte ich diesen Prozess für die ganze Weltgemeinschaft öffnen. Ich werde jedoch interessiert sein, was bei der Lösung dieser Probleme erreicht werden kann und welche Methoden in diesem Fall verwendet werden können.
Regel 30 - Zu lösende Aufgaben
In Bezug auf die Wettbewerbsaufgaben nach Regel 30 gebe ich einem der Hauptmerkmale des Algorithmus von Regel 30 Vorrang, nämlich der
offensichtlichen Zufälligkeit der Bildung der Zellen seiner zentralen Spalte . Beginnen Sie mit einer schwarzen Zelle und sehen Sie sich dann die Reihenfolge der Farbwerte der Zellen in dieser Spalte an. Sie werden zu dem Schluss kommen, dass sie zufällig sind:

CodeArrayPlot[
MapIndexed[If[#2[[2]] != 21, # /. {0 -> 0.2, 1 -> .6}, #] &,
CellularAutomaton[30, {{1}, 0}, 20], {2}], Mesh -> All]
Aber in welchem Sinne sind sie
"wirklich zufällig" ? Und kann diese Annahme bewiesen werden? Jede der im Rahmen des Wettbewerbs festgelegten Aufgaben verwendet ein eigenes Zufälligkeitskriterium und fragt danach, ob die Reihenfolge gemäß diesem Kriterium zufällig ist.
Aufgabe 1: Bleibt die zentrale Spalte immer nicht periodisch?
Betrachten Sie den Anfang der zentralen Spalte von Regel 30:

CodeArrayPlot[List@CellularAutomaton[30, {{1}, 0}, {80, {{0}}}],
Mesh -> True, ImageSize -> Full]
Es ist nicht schwer festzustellen, dass die Werte in dieser Spalte nicht wiederholt werden - sie sind nicht periodisch. Die Herausforderung ist jedoch, ob die zentrale Säule jemals periodisch wird. Durch das Starten von Regel 30 sehen wir, dass die Sequenz selbst in den
ersten Milliarden Schritten nicht periodisch
wird . Was muss getan werden, um dies mit Sicherheit festzustellen und zu beweisen?
Hier befindet sich der Link, über den sich die
ersten Millionen und
ersten Milliarden Werte dieser Sequenz befinden (
Wolfram Data Warehouse ).
Aufgabe 2: Ist jede Farbe der Zelle (schwarz oder weiß) im Durchschnitt in der mittleren Spalte gleich wahrscheinlich?
Dies erhalten wir, wenn wir die Anzahl der schwarzen und weißen Zellen nacheinander in mehr Schritten in der mittleren Spalte des Regel 30-Algorithmus zählen:

CodeDataset[{{1, 1, 0, ""}, {10, 7, 3, 2.3333333333333335}, {100, 52, 48, 1.0833333333333333},
{1000, 481, 519, 0.9267822736030829}, {10000, 5032, 4968, 1.0128824476650564},
{100000, 50098, 49902, 1.0039276982886458}, {1000000, 500768, 499232,
1.003076725850907}, {10000000, 5002220, 4997780, 1.0008883944471345},
{100000000, 50009976, 49990024, 1.000399119632349},
{1000000000, 500025038, 499974962, 1.0001001570154626}}]
Die Ergebnisse sind für schwarze und weiße Zellen sicherlich nahezu gleich. Hier ist die Problematik (Frage des Problems) die Frage,
ob diese Beziehung mit zunehmender Anzahl von Schritten im Zyklus gegen 1 konvergiert .
Aufgabe 3: Erfordert die Berechnung der n-ten Zelle der zentralen Spalte mindestens O ( n ) -Operationen?
Um die
n-te Zelle in der mittleren Spalte zu finden, können Sie immer einfach Regel 30 für
n Schritte ausführen und die Werte aller Zellen innerhalb des in der folgenden Abbildung ausgewählten Diamanten berechnen:

CodeWith[{n = 100},
ArrayPlot[
MapIndexed[If[Total[Abs[#2 - n/2 - 1]] <= n/2, #, #/4] &,
CellularAutomaton[30, CenterArray[{1}, n + 1], n], {2}]]]
Aber wenn Sie es direkt tun, wird es
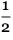 n 2
n 2 separate Zellenaktualisierungen, daher steigt die erforderliche Rechenleistung mit O (
n 2 ). Die Frage dieses Problems ist,
ob es eine mehr (oder die schnellste) Methode gibt, um den Wert der n-ten Zelle ohne alle Zwischenberechnungen zu berechnen - oder insbesondere in weniger als O ( n ) Operationen .
Die Zahlen, aus denen Pi besteht
Regel 30 ist ein Produkt des Computeruniversums: ein System, das auf der Untersuchung möglicher einfacher Programme mit einer neuen intellektuellen Struktur basiert, die durch das Paradigma des Computing bereitgestellt wird. Die
Aufgaben, die ich im Wettbewerb um Regel 30 definiert habe, haben jedoch Analoga in der Mathematik, die es schon seit Jahrhunderten gibt .
Betrachten Sie die
Werte der Zahlen in der Zahl Pi . Das Verhalten dieser Zahlen ähnelt der Generierung von Daten in der zentralen Spalte des Regel-30-Algorithmus. Das heißt, es gibt einen bestimmten Algorithmus für deren Berechnung, und sobald sie formuliert sind, scheinen sie für alle Aufgaben fast zufällig zu sein.
![N [Pi, 85] N[Pi, 85]](https://habrastorage.org/getpro/habr/post_images/49e/ae6/17d/49eae617de3c0c9a864d4624413c6ce8.png)
Um das Analogon etwas näher zu bringen, hier die ersten Ziffern von Pi im Zahlensystem mit Basis 2:
![BaseForm [N [Pi, 25], 2] BaseForm[N[Pi, 25], 2]](https://habrastorage.org/getpro/habr/post_images/18e/d4b/8f6/18ed4b8f6fd778443cc62470ea0956a9.png)
CodeBaseForm[N[Pi, 25], 2]
Und hier sind die ersten paar Bits in der mittleren Spalte von Regel 30:
![Zeile [CellularAutomaton [30, {{1}, 0}, {90, {{0}}}] Row[CellularAutomaton[30, {{1}, 0}, {90, {{0}}}]]](https://habrastorage.org/getpro/habr/post_images/9e9/f64/a52/9e9f64a521480621d3adbb859609742a.png)
CodeRow[CellularAutomaton[30, {{1}, 0}, {90, {{0}}}]]
Zum Spaß können Sie sie in Dezimalzahlen konvertieren:
![N [FromDigits [{Flatten [CellularAutomaton [30, {{1}, 0}, {500, {0}}], 0}, 2], 85] N[FromDigits[{Flatten[CellularAutomaton[30, {{1}, 0}, {500, {0}}]], 0}, 2], 85]](https://habrastorage.org/getpro/habr/post_images/0df/d67/782/0dfd677828ca278c971d267948d88ad3.png)
CodeN[FromDigits[{Flatten[CellularAutomaton[30, {{1}, 0}, {500, {0}}]],
0}, 2], 85]
Natürlich sind die bekannten Algorithmen zum Berechnen der Ziffern von Pi viel komplizierter als die relativ einfache Regel zum Erzeugen von Zellen in der mittleren Spalte von Regel 30. Was wissen wir also über Ziffern in Pi?
Erstens wissen wir, dass sie nicht wiederholt werden. Dies wurde bereits in den 60er Jahren des 18. Jahrhunderts bewiesen, als gezeigt wurde,
dass Pi eine irrationale Zahl ist , da die einzigen Zahlen, in denen sich die Zahlen wiederholen, rationale Zahlen sind. (
1882 wurde auch
gezeigt, dass Pi transzendent ist, dh dass es nicht durch die Wurzeln von Polynomen ausgedrückt werden kann).
Welche Art von Analogie kann mit der Formulierung von Problem 2 gezogen werden? Wissen wir, dass in einer Folge von
Pi- Ziffern unterschiedliche Ziffern mit derselben Frequenz auftreten? Bisher
wurden mehr als
100 Billionen Binärziffern berechnet - und die gemessenen Ziffernfrequenzen liegen sehr nahe beieinander (in den ersten
40 Billionen Binärziffern von Pi beträgt
das Verhältnis von Einheiten zu Nullen ungefähr 0,99999998064). Aber sind die Frequenzen bei der Berechnung des Grenzwerts genau gleich? Wissenschaftler haben diese Frage seit mehreren Jahrhunderten gestellt, aber bisher konnte die Mathematik keine Antwort darauf geben.
Bei rationalen Zahlen sind die Ziffernfolgen, aus denen sie bestehen, periodisch, und es ist leicht, die relativen Häufigkeit des Auftretens dieser Zahlen in einer Zahl zu bestimmen. Für die Ziffernfolge aller anderen „von der Natur geschaffenen (natürlich konstruierten)“ Zahlen ist jedoch in den meisten Fällen praktisch nichts darüber bekannt, wozu die Häufigkeit der in der Zahl enthaltenen Ziffern tendenziell neigt. Es wäre logisch anzunehmen, dass tatsächlich die Ziffern von Pi (sowie die zentrale Spalte von Regel 30) in dem Sinne „
normal “ sind, dass nicht nur jede einzelne Ziffer, sondern auch jeder Ziffernblock einer bestimmten Länge dieselbe Grenzfrequenz aufweist. Und wie in den Arbeiten zu diesem Thema der 1930er Jahre festgestellt wurde, ist es durchaus möglich, "eine digitale Konstruktion (Modell)" aus normalen Zahlen zu bauen.
Die Champernonkonstante, die durch Kombinieren der Ziffern aufeinanderfolgender Ganzzahlen erhalten wird, ist ein Beispiel für die obige Argumentation (dieselbe kann auf der Grundlage einer beliebigen normalen Zahl erhalten werden, indem die Werte der Funktionen aufeinanderfolgender Ganzzahlen kombiniert werden):
![N [ChampernowneNumber [10], 85] N[ChampernowneNumber[10], 85]](https://habrastorage.org/getpro/habr/post_images/253/f93/8f3/253f938f3261e70f8985a49bf1158dde.png)
CodeN[ChampernowneNumber[10], 85]
Es sollte beachtet werden, dass der Punkt hier ist, dass für "natürlich konstruierte" Zahlen, die durch Kombinationen von mathematischen Standardfunktionen gebildet werden, kein einziges entdecktes Beispiel gefunden wird, bei dem eine reguläre Folge von Zahlen gefunden würde. Letztendlich hängt diese Bestimmung natürlich davon ab, was unter „Regelmäßigkeit“ zu verstehen ist, und irgendwann wird die Aufgabe zu einer Art
Digital-Analog-Suche nach außerirdischer Intelligenz . Es gibt jedoch keine Hinweise darauf, dass es beispielsweise nicht möglich ist, eine komplexe Kombination von Quadratwurzeln zu finden, die eine Folge von Zahlen mit einer sehr offensichtlichen Regelmäßigkeit aufweisen würden.
Betrachten Sie zum Schluss das Analogon von Problem 3 für Pi? Im Gegensatz zu Regel 30, bei der die offensichtliche Methode zur Berechnung der Elemente in einer Sequenz Schritt für Schritt ist, umfassen herkömmliche Methoden zur Berechnung der Ziffern von Pi das Erhalten der besten Annäherungen an Pi als exakte Zahl. Mit der 1910 von
Ramanujan erfundenen und 1989
von den Brüdern Chudnovsky verbesserten Standardreihe („bizarr“) geben die ersten Mitglieder dieser Reihe die folgenden Näherungswerte an:

CodeStyle[Table[N[(12*\!\(
\*UnderoverscriptBox[\(\[Sum]\), \(k = 0\), \(n\)]
\*FractionBox[\(
\*SuperscriptBox[\((\(-1\))\), \(k\)]*\(\((6*k)\)!\)*\((13591409 +
545140134*k)\)\), \(\(\((3*k)\)!\)
\*SuperscriptBox[\((\(k!\))\), \(3\)]*
\*SuperscriptBox[\(640320\), \(3*k + 3/2\)]\)]\))^-1, 100], {n, 10}] //
Column, 9]
Wie viele Operationen sind also erforderlich, um die
n-te Ziffer zu finden? Die Anzahl der in der Zeile erforderlichen Begriffe ist O (
n ). Jede Bedingung muss jedoch mit einer
n- stelligen Genauigkeit berechnet werden, was mindestens O (
n ) separate Rechenoperationen erfordert, was bedeutet, dass die Rechenarbeitslast im Allgemeinen größer als O (
n ) ist.
Bis in die 1990er Jahre wurde angenommen, dass es keine Möglichkeit gibt, die
n-te Ziffer von Pi zu berechnen, ohne alle vorherigen zu berechnen. 1995 entdeckte
Simon Pluff jedoch , dass es tatsächlich möglich ist, die
n-te Ziffer mit einiger Wahrscheinlichkeit zu berechnen, ohne die vorherigen zu berechnen. Und obwohl man denken würde, dass dies Ihnen erlauben würde, die
n-te Ziffer in weniger als O (
n ) Operationen zu erhalten, bedeutet die Tatsache, dass Sie Berechnungen mit einer Genauigkeit von
n Ziffern durchführen müssen, dass mindestens
O ( n ) Operationen.
Ergebnisse, Analogien und Intuition
Aufgabe 1: Bleibt die zentrale Spalte immer nicht periodisch?
Von den drei Preisen des Wettbewerbs nach Regel 30 ist dies derjenige, bei dem die meisten Fortschritte bei der Lösung dieses Problems bereits erzielt wurden. Da noch nicht bekannt ist, ob die zentrale Spalte von Regel 30 periodisch wird, hat
Erica Jen 1986
gezeigt, dass keine zwei Spalten periodisch sein können. Tatsächlich ist dies so, und man kann auch dafür argumentieren,
dass eine Spalte in Kombination mit einzelnen Zellen in einer anderen Spalte nicht periodisch sein kann .
Der Beweis des Spaltenpaars verwendet ein Merkmal von Regel 30. Betrachten Sie die Struktur der Regel:
![RulePlot [CellularAutomaton [30]] RulePlot[CellularAutomaton[30]]](https://habrastorage.org/getpro/habr/post_images/5fa/ca7/858/5faca785893d90e7969ef2a4dad73c58.png)
CodeRulePlot[CellularAutomaton[30]]
Man kann einfach sagen, dass die Regel für jedes Dreifach von Zellen die Farbe der zentralen Zelle bestimmt, aber für Regel 30 können Sie die Regel auch effektiv zur Seite ausführen: Unter Berücksichtigung der Zelle rechts und darüber können Sie auch die Farbe der Zelle links eindeutig bestimmen. Wenn Sie also zwei benachbarte Spalten verwenden, können
Sie die gesamte Vorlage auf der linken Seite wiederherstellen :

CodeGraphicsRow[
ArrayPlot[#, PlotRange -> 1, Mesh -> All, PlotRange -> 1,
Background -> LightGray,
ImageSize -> {Automatic, 80}] & /@ (PadLeft[#, {Length[#], 10},
10] & /@
Module[{data = {{0, 1}, {1, 1}, {0, 0}, {0, 1}, {1, 1}, {1,
0}, {0, 1}, {1, 10}}},
Flatten[{{data},
Table[Join[
Table[Module[{p, q = data[[n, 1]], r = data[[n, 2]],
s = data[[n + 1, 1]] },
p = Mod[-q - r - qr + s, 2];
PrependTo[data[[n]], p]], {n, 1, Length[data] - i}],
PrependTo[data[[-#]], 10] & /@ Reverse[Range[i]]], {i, 7}]},
1]])]
Wenn die Spalten jedoch eine periodische Struktur hätten, würde sich unmittelbar daraus ergeben, dass die wiederhergestellte Vorlage auch periodisch sein sollte. So sind beispielsweise konstruktionsbedingt zumindest die Anfangsbedingungen definitiv nicht periodisch, und daher können beide Spalten nicht periodisch sein. Die gleiche Aussage gilt, wenn die Spalten nicht benachbart sind und wenn nicht alle Zellen in beiden Spalten bekannt sind. Es ist jedoch kein Weg bekannt, diese Bestimmung auf eine einzelne Spalte, wie z. B. eine zentrale Spalte, zu verteilen, und daher wird die erste Aufgabe des Wettbewerbs gemäß Regel 30 nicht gelöst.
Also, was kann verwendet werden, um es zu lösen? Wenn sich herausstellt, dass die zentrale Spalte letztendlich periodisch ist, können Sie sie einfach berechnen. Wir wissen, dass es für die ersten Milliarden Schritte nicht periodisch ist, aber wir können zumindest davon ausgehen, dass es einen Übergangsprozess mit Billionen von Schritten gibt, nach dem es periodisch wird.
Halten Sie das für glaubwürdig?
Transienten treten auf - und theoretisch (wie beim klassischen
Problem des Stoppens einer Turing-Maschine ) können sie sogar beliebig lang sein. Hier sehen wir uns ein Beispiel an - gefunden während der Suche -
Regeln mit 4 möglichen Farben (allgemeiner Code 150898). Angenommen, wir führen 200 Schritte aus, und wie Sie sehen können, ist die zentrale Spalte völlig zufällig:

CodeArrayPlot[
CellularAutomaton[{150898, {4, 1}, 1}, {{1}, 0}, {200, 150 {-1, 1}}],
ColorRules -> {0 -> Hue[0.12, 1, 1], 1 -> Hue[0, 0.73, 0.92],
2 -> Hue[0.13, 0.5, 1], 3 -> Hue[0.17, 0, 1]},
PixelConstrained -> 2, Frame -> False]
Nach 500 Schritten sieht die gesamte Vorlage völlig zufällig aus:

CodeArrayPlot[
CellularAutomaton[{150898, {4, 1}, 1}, {{1}, 0}, {500, 300 {-1, 1}}],
ColorRules -> {0 -> Hue[0.12, 1, 1], 1 -> Hue[0, 0.73, 0.92],
2 -> Hue[0.13, 0.5, 1], 3 -> Hue[0.17, 0, 1]}, Frame -> False,
ImagePadding -> 0, PlotRangePadding -> 0, PixelConstrained -> 1]
Hier können Sie sehen, dass bei Annäherung an die zentrale Spalte etwas Überraschendes passiert: Nach 251 Schritten scheint die zentrale Spalte auf einen festen Wert (oder zumindest auf die nächsten mehr als eine Million Schritte) wiedergeboren zu sein:

CodeGrid[{ArrayPlot[#, Mesh -> True,
ColorRules -> {0 -> Hue[0.12, 1, 1], 1 -> Hue[0, 0.73, 0.92],
2 -> Hue[0.13, 0.5, 1], 3 -> Hue[0.17, 0, 1]}, ImageSize -> 38,
MeshStyle -> Lighter[GrayLevel[.5, .65], .45]] & /@
Partition[
CellularAutomaton[{150898, {4, 1}, 1}, {{1}, 0}, {1400, {-4, 4}}],
100]}, Spacings -> .35]
Könnte der gleiche Übergang in Regel 30 stattfinden? Betrachten Sie die Muster aus Regel 30 und wählen Sie diejenigen aus, bei denen die Diagonalen links periodisch sind:

Codesteps = 500;
diagonalsofrule30 =
Reverse /@
Transpose[
MapIndexed[RotateLeft[#1, (steps + 1) - #2[[1]]] &,
CellularAutomaton[30, {{1}, 0}, steps]]];
diagonaldataofrule30 =
Table[With[{split =
Split[Partition[Drop[diagonalsofrule30[[k]], 1], 8]],
ones = Flatten[
Position[Reverse[Drop[diagonalsofrule30[[k]], 1]],
1]]}, {Length[split[[1]]], split[[1, 1]],
If[Length[split] > 1, split[[2, 1]],
Length[diagonalsofrule30[[k]]] - Floor[k/2]]}], {k, 1,
2 steps + 1}];
transientdiagonalrule30 = %;
transitionpointofrule30 =
If[IntegerQ[#[[3]]], #[[3]],
If[#[[1]] > 1,
8 #[[1]] + Count[Split[#[[2]] - #[[3]]][[1]], 0] + 1, 0] ] & /@
diagonaldataofrule30;
decreasingtransitionpointofrule30 =
Append[Min /@ Partition[transitionpointofrule30, 2, 1], 0];
transitioneddiagonalsofrule30 =
Table[Join[
Take[diagonalsofrule30[[n]],
decreasingtransitionpointofrule30[[n]]] + 2,
Drop[diagonalsofrule30[[n]],
decreasingtransitionpointofrule30[[n]]]], {n, 1, 2 steps + 1}];
transientdiagonalrule30 =
MapIndexed[RotateRight[#1, (steps + 1) - #2[[1]]] &,
Transpose[Reverse /@ transitioneddiagonalsofrule30]];
smallertransientdiagonalrule30 =
Take[#, {225, 775}] & /@ Take[transientdiagonalrule30, 275];
Framed[ArrayPlot[smallertransientdiagonalrule30,
ColorRules -> {0 -> White, 1 -> Gray, 2 -> Hue[0.14, 0.55, 1],
3 -> Hue[0.07, 1, 1]}, PixelConstrained -> 1,
Frame -> None,
ImagePadding -> 0, ImageMargins -> 0,
PlotRangePadding -> 0, PlotRangePadding -> Full
], FrameMargins -> 0, FrameStyle -> GrayLevel[.75]]
Anscheinend gibt es eine Grenze, die die Reihenfolge links von der Störung rechts trennt. Und zumindest für die ersten 100.000 Schritte scheint sich die Grenze bei jedem Schritt durchschnittlich um etwa 0,252 Schritte nach links zu verschieben -
mit einigen zufälligen Abweichungen :
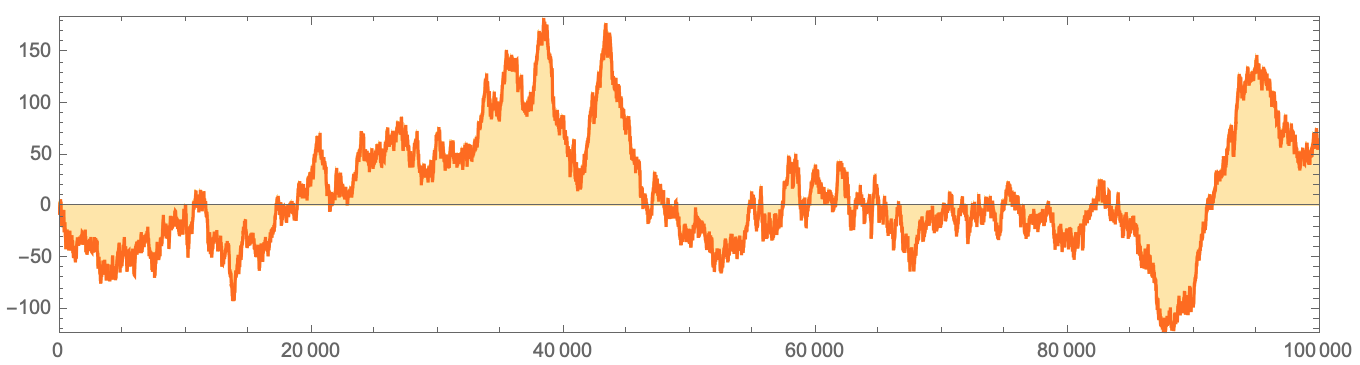
Codedata = CloudGet[
CloudObject[
"https://www.wolframcloud.com/obj/bc470188-f629-4497-965d-\
a10fe057e2fd"]];
ListLinePlot[
MapIndexed[{First[#2], -# - .252 First[#2]} &,
Module[{m = -1, w},
w = If[First[#] > m, m = First[#], m] & /@ data[[1]]; m = 1;
Table[While[w[[m]] < i, m++]; m - i, {i, 100000}]]],
Filling -> Axis, AspectRatio -> 1/4, MaxPlotPoints -> 10000,
Frame -> True, PlotRangePadding -> 0, AxesOrigin -> {Automatic, 0},
PlotStyle -> Hue[0.07`, 1, 1],
FillingStyle -> Directive[Opacity[0.35`], Hue[0.12`, 1, 1]]]
Aber wie können wir schließlich herausfinden, an welchem Punkt diese Schwankungen nicht mehr signifikant sind, so dass sie die linke Reihenfolge zwingen, die mittlere Spalte zu überqueren und möglicherweise sogar die gesamte Vorlage periodisch zu machen? Nach den verfügbaren Daten zu urteilen, scheint die Annahme unwahrscheinlich, obwohl ich nicht genau sagen kann, wie dies bestimmt werden kann.
Dies ist natürlich genau der Fall, der die Existenz von Systemen mit außergewöhnlich langen "Transienten" veranschaulicht. Betrachten Sie nun die Verteilung der Primzahlen und berechnen Sie
LogIntegral [
n ] -
PrimePi [
n ].
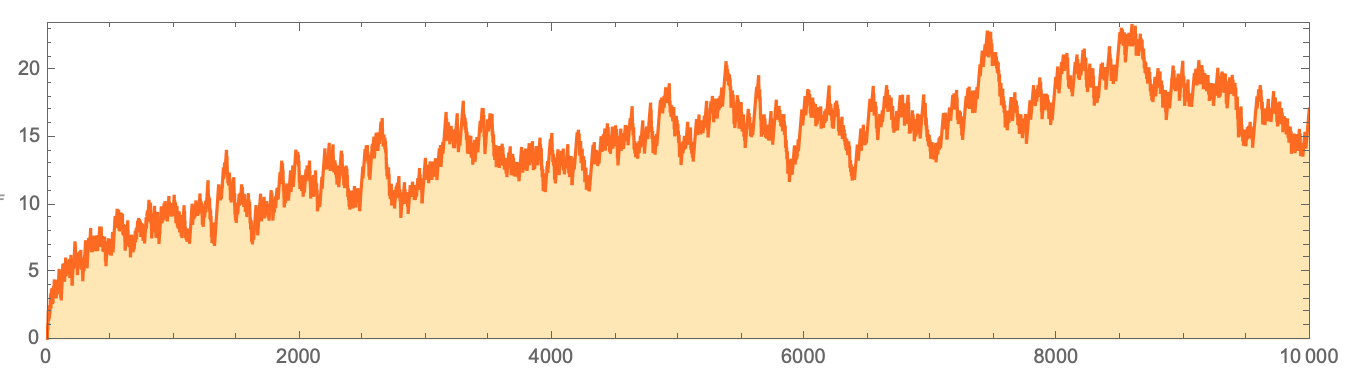
CodeDiscretePlot[LogIntegral[n] - PrimePi[n], {n, 10000},
Filling -> Axis,
Frame -> True, PlotRangePadding -> 0, AspectRatio -> 1/4,
Joined -> True, PlotStyle -> Hue[0.07`, 1, 1],
FillingStyle -> Directive[Opacity[0.35`], Hue[0.12`, 1, 1]]]
Ja, es gibt Schwankungen, aber in dieser Abbildung sieht es so aus, als ob dieser Unterschied immer im positiven Bereich liegt. Und das ist zum Beispiel das, worüber Ramanujan gesprochen hat, aber am Ende
stellt sich heraus, dass dies nicht so ist . Am Anfang war die Grenze, an der er versagte, für diese Zeit astronomisch groß (
Skives Nummer 10
10 10 964 ). Und obwohl noch niemand einen expliziten Wert von
n gefunden hat, für den die Differenz negativ ist, ist bekannt, dass er bis zu
n = 10
317 existieren muss (und letztendlich wird die Differenz negativ sein).
Ich bin der Meinung, dass der zentralen Spalte von Regel 30 nichts dergleichen passiert, aber bisher haben wir keine Beweise dafür, dass dies unmöglich ist, dies kann nicht argumentiert werden.
Es ist anzumerken, dass man davon ausgehen kann, dass, obwohl es grundsätzlich möglich ist, Periodizität durch Offenlegung der Regelmäßigkeit in der zentralen Spalte von Regel 30 nachzuweisen, nichts dergleichen für Nichtperiodizität getan werden kann. Es ist bekannt, dass es Muster gibt, deren zentrale Spalten nicht periodisch sind, obwohl sie sehr regelmäßig sind. Die Hauptklasse solcher Beispiele sind verschachtelte Vorlagen. Hier ist zum Beispiel eine sehr einfache Darstellung aus Regel 161, in der die mittlere Spalte weiße Zellen hat, wenn
n = 2
k :

CodeGraphicsRow[
ArrayPlot[CellularAutomaton[161, {{1}, 0}, #]] & /@ {40, 200}]
Und hier ist ein
etwas komplexeres Beispiel (aus der Zweifarbenregel 69540422 für zwei Nachbarn) , in dem die zentrale Spalte eine
Thue-Morse-Sequenz -
ThueMorse [
n ] ist:

CodeGraphicsRow[
ArrayPlot[
CellularAutomaton[{69540422, 2, 2}, {{1},
0}, {#, {-#, #}}]] & /@ {40, 400}]
Wir können annehmen, dass die Thue-Morse-Sequenz durch die sequentielle Anwendung der Substitution erzeugt wird:

CodeRulePlot[SubstitutionSystem[{0 -> {0, 1}, 1 -> {1, 0}}],
Appearance -> "Arrow"]
Es stellt sich heraus, dass der
n-te Term in dieser Sequenz als
Mod [
DigitCount [
n , 2, 1], 2] festgelegt ist - dieses Objekt wird niemals periodisch sein.
Könnte es sein, dass die zentrale Spalte von Regel 30 durch
Ersetzen generiert werden kann? Wenn dies so ist, würde mich diese Tatsache überraschen (obwohl es
natürliche Beispiele zu geben
scheint, wenn sehr komplexe Substitutionssysteme auftreten ), aber auch hier, solange es keine Beweise dafür gibt.
Es ist zu beachten, dass alle Wettbewerbsaufgaben aus Regel 30 bei der Formulierung eines Algorithmus berücksichtigt werden, der auf einer unendlichen Anzahl von Zellen ausgeführt wird. ,
n , , ( )? , 2
n —
, , .
n =5:

CodeGraph[# -> CellularAutomaton[30][#] & /@ Tuples[{1, 0}, 4],
VertexLabels -> ((# ->
ArrayPlot[{#}, ImageSize -> 30, Mesh -> True]) & /@
Tuples[{1, 0}, 4])]
n =5
n =11:

CodeRow[Table[
Framed[Graph[# -> CellularAutomaton[30][#] & /@
Tuples[{1, 0}, n]]], {n, 4, 11}]]
, , , , . , 2
n ( , ,
).
,
n 30 ,
, 2 n .
, ( ):
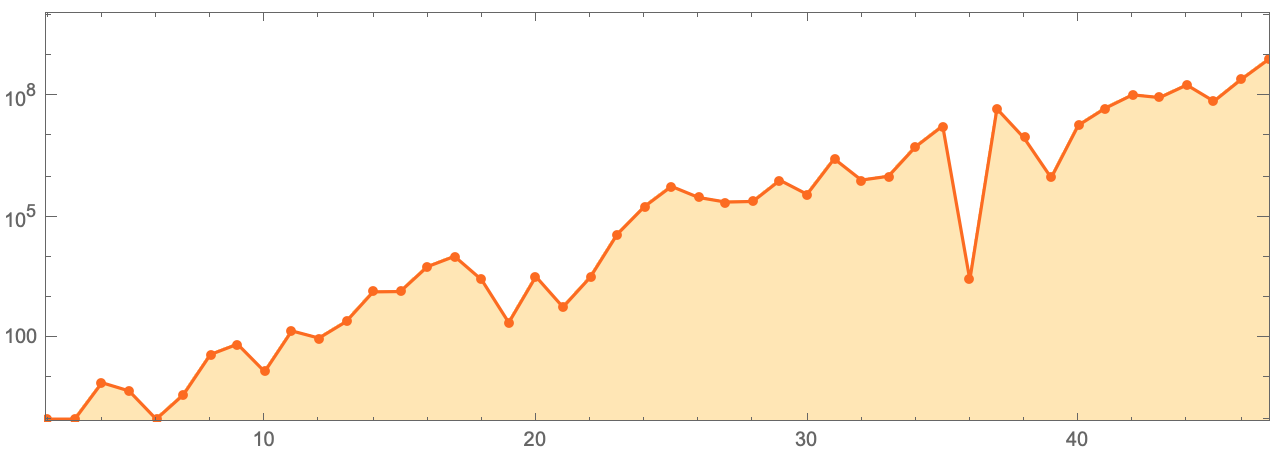
CodeListLogPlot[
Normal[Values[
ResourceData[
"Repetition Periods for Elementary Cellular Automata"][
Select[#Rule == 30 &]][All, "RepetitionPeriods"]]],
Joined -> True, Filling -> Bottom, Mesh -> All,
MeshStyle -> PointSize[.008], AspectRatio -> 1/3, Frame -> True,
PlotRange -> {{47, 2}, {0, 10^10}}, PlotRangePadding -> .1,
PlotStyle -> Hue[0.07`, 1, 1],
FillingStyle -> Directive[Opacity[0.35`], Hue[0.12`, 1, 1]]]
, ,
n 2
0.63 n . , , . , , ? .
2: ?
10000 30:
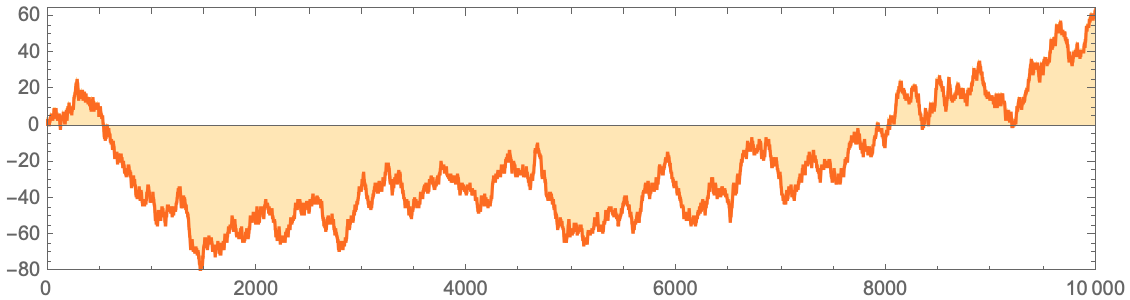
CodeRListLinePlot[
Accumulate[2 CellularAutomaton[30, {{1}, 0}, {10^4 - 1, {{0}}}] - 1],
AspectRatio -> 1/4, Frame -> True, PlotRangePadding -> 0,
AxesOrigin -> {Automatic, 0}, Filling -> Axis,
PlotStyle -> Hue[0.07`, 1, 1],
FillingStyle -> Directive[Opacity[0.35`], Hue[0.12`, 1, 1]]]
:
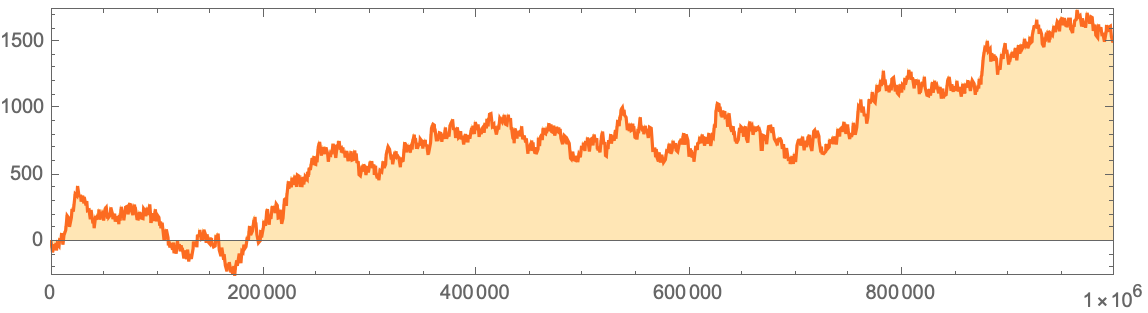
CodeListLinePlot[
Accumulate[
2 ResourceData[
"A Million Bits of the Center Column of the Rule 30 Cellular Automaton"] - 1], Filling -> Axis, Frame -> True, PlotRangePadding -> 0, AspectRatio -> 1/4, MaxPlotPoints -> 1000, PlotStyle -> Hue[0.07`, 1, 1],
FillingStyle -> Directive[Opacity[0.35`], Hue[0.12`, 1, 1]]]
:
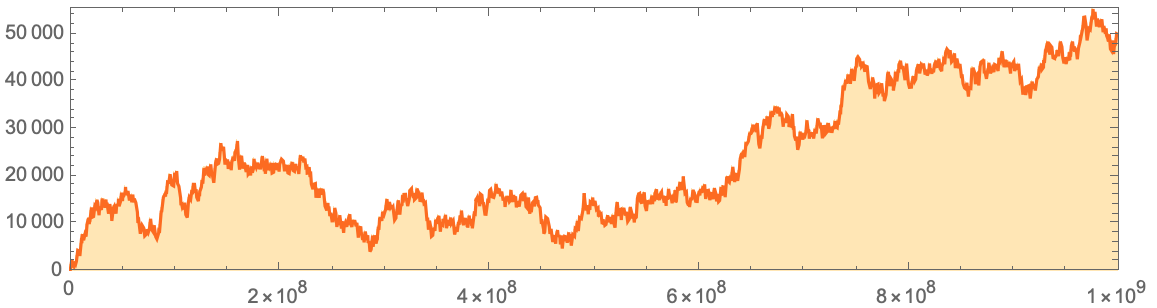
Codedata=Flatten[IntegerDigits[#,2,8]&/@Normal[ResourceData["A
Billion Bits of the Center Column of the Rule 30 Cellular Automaton"]]];
data=Accumulate[2 data-1];
sdata=Downsample[data,10^5];
ListLinePlot[Transpose[{Range[10000] 10^5,sdata}],Filling->Axis,Frame->True,PlotRangePadding->0,AspectRatio->1/4,MaxPlotPoints->1000,PlotStyle->Hue[0.07`,1,1],FillingStyle->Directive[Opacity[0.35`],Hue[0.12`,1,1]]]
, , 1 () 0 (), , , , , , , .
. 10 000 :

CodeQuiet[ListLinePlot[
MapIndexed[#/(First[#2] - #) &,
Accumulate[CellularAutomaton[30, {{1}, 0}, {10^4 - 1, {{0}}}]]],
AspectRatio -> 1/4, Filling -> Axis, AxesOrigin -> {Automatic, 1},
Frame -> True, PlotRangePadding -> 0, PlotStyle -> Hue[0.07`, 1, 1],
FillingStyle -> Directive[Opacity[0.35`], Hue[0.12`, 1, 1]],
PlotRange -> {Automatic, {.88, 1.04}}]]
, 1? …
, :
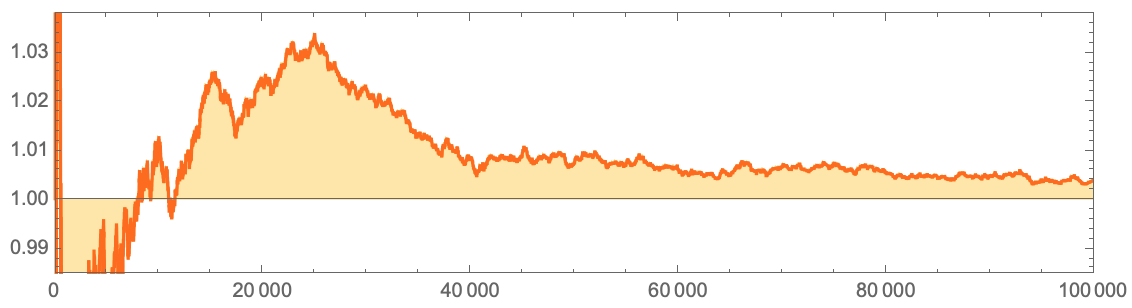
CodeQuiet[ListLinePlot[
MapIndexed[#/(First[#2] - #) &,
Accumulate[CellularAutomaton[30, {{1}, 0}, {10^5 - 1, {{0}}}]]],
AspectRatio -> 1/4, Filling -> Axis, AxesOrigin -> {Automatic, 1},
Frame -> True, PlotRangePadding -> 0, PlotStyle -> Hue[0.07`, 1, 1],
FillingStyle -> Directive[Opacity[0.35`], Hue[0.12`, 1, 1]],
PlotRange -> {Automatic, {.985, 1.038}}]]
, , . 1 , :
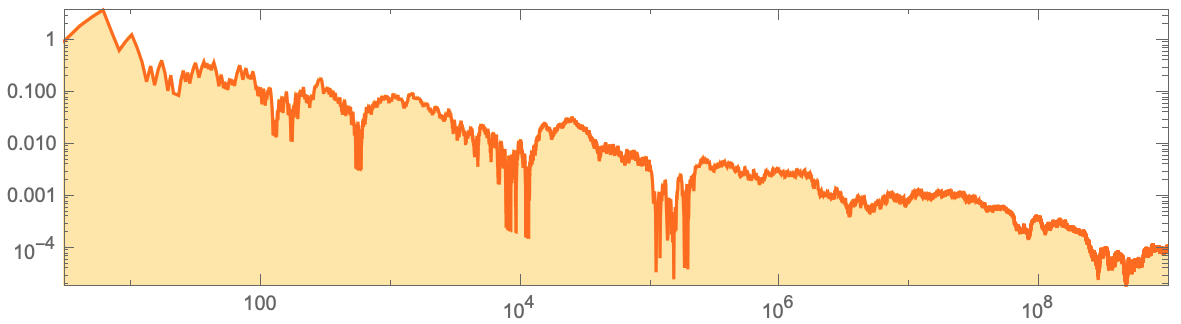
Codeaccdata=Accumulate[Flatten[IntegerDigits[#,2,8]&/@Normal[ResourceData["A
Billion Bits of the Center Column of the Rule 30 Cellular Automaton"]]]];
diffratio=FunctionCompile[Function[Typed[arg,TypeSpecifier["PackedArray"]["MachineInteger",1]],MapIndexed[Abs[N[#]/(First[#2]-N[#])-1.]&,arg]]];
data=diffratio[accdata];
ListLogLogPlot[Join[Transpose[{Range[3,10^5],data[[3;;10^5]]}],Transpose[{Range[10^5+1000,10^9,1000],data[[10^5+1000;;10^9;;1000]]}]],Joined->True,AspectRatio->1/4,Frame->True,Filling->Axis,PlotRangePadding->0,PlotStyle->Hue[0.07`,1,1],FillingStyle->Directive[Opacity[0.35`],Hue[0.12`,1,1]]]
, ? . , . , , , , .
, , 30, .
, ,
k . , 2
k . , - , , , , 30
k ( ).
,
. , ,
k =22, 2
k , , :

CodeListLogPlot[{3, 7, 13, 63, 116, 417, 1223, 1584, 2864, 5640, 23653,
42749, 78553, 143591, 377556, 720327, 1569318, 3367130, 7309616,
14383312, 32139368, 58671803}, Joined -> True, AspectRatio -> 1/4,
Frame -> True, Mesh -> True,
MeshStyle ->
Directive[{Hue[0.07, 0.9500000000000001, 0.99], PointSize[.01]}],
PlotTheme -> "Detailed",
PlotStyle -> Directive[{Thickness[.004], Hue[0.1, 1, 0.99]}]]
, , . , –
, , .
—
— , , ,
, , , 30,
, ,
, , .
30 , , «
», , , , , , . , «»: 30, , , , , , , , 30.
, . 30, , - ,
, , 30, , , - .
. 30
, , . , , 30 - ( ), , , , 30. 200 :

CodeListLinePlot[
FromDigits[{#, 0}, 2] & /@
CellularAutomaton[30, {{1}, 0}, {200, {0, 200}}], Mesh -> All,
AspectRatio -> 1/4, Frame -> True,
MeshStyle ->
Directive[{Hue[0.07, 0.9500000000000001, 0.99], PointSize[.0085]}],
PlotTheme -> "Detailed", PlotStyle -> Directive[{
Hue[0.1, 1, 0.99]}], ImageSize -> 575]
, :

CodeGrid[{Table[
Histogram[
FromDigits[{#, 0}, 2] & /@
CellularAutomaton[30, {{1}, 0}, {10^n, {0, 20}}], {.01},
Frame -> True,
FrameTicks -> {{None,
None}, {{{0, "0"}, .2, .4, .6, .8, {1, "1"}}, None}},
PlotLabel -> (StringTemplate["`` steps"][10^n]),
ChartStyle -> Directive[Opacity[.5], Hue[0.09, 1, 1]],
ImageSize -> 208,
PlotRangePadding -> {{0, 0}, {0, Scaled[.06]}}], {n, 4, 6}]},
Spacings -> .2]
, , , 0 1.
1900- . , ,
FractionalPart [
hn ]
n h . ,
FractionalPart [
h n ]
h (
), —
FractionalPart [(3/2)
n ] — . (,
, 16- , , 2-
FractionalPart [16
x n -1 +
r [
n ]],
r [
n ]
n .)
3: n- O( n ) ?
,
150 :

CodeRow[{ArrayPlot[CellularAutomaton[150, {{1}, 0}, 30], Mesh -> All,
ImageSize -> 315],
ArrayPlot[CellularAutomaton[150, {{1}, 0}, 200], ImageSize -> 300]}]
, ( ), , :

CodeArrayPlot[{Table[Mod[IntegerExponent[t, 2], 2], {t, 80}]},
Mesh -> All, ImageSize -> Full]
n- ? , ,
:
Mod [
IntegerExponent [
n , 2], 2]. ,
n , , .
, « »? ,
n ,
Log [2,
n ] . , , O(log
n ) .
- 30? ,
n- , 30
n 2 , , . , -, , , — , , , , , .
« » (,
, . .), , , , , (,
,
3D- . .), .
,
1980- , , , ,
, , , .
, 3 30 , , . ( O(
n ) ; O(
n α ) α <2, , , O(log
β (
n )) — , , .)
3 , ,
n- , O(
n ), 150 .
O (
n )? () , « »?
, — — , , .
,
. , , ,
n , ,
,
n , (, «», O(log
n ) .
, . , , , ,
Wolfram Language . « ». , , Wolfram Language
, .
, 30 , 3 , , , , , ,
n- , O(
n ) , .
, , . , ,
. , , , , , — , O(log
n ) ,
n .
,
P NP . , 30 ( P
LOGTIME ), , , , . , , ,
n n , O(
n 2 ) , , P (« »), , , , , NP. («») , , , , 2
n .
, 2
n , , . ,
NP- , , , NP . 30 NP-? , , ( - , 30
NP).
30 . : 30 , , 30, «» , , , , .
, 256
110 ( , ),
110 , ,
, . , , , «» 110 .

CodeSeedRandom[23542345]; ArrayPlot[
CellularAutomaton[110, RandomInteger[1, 600], 400],
PixelConstrained -> 1]
30, , — , «» , . ,
, 30 , , ,
, .
, , , , , 30. , , (, )
, , . , , — , . , .
, , 3.
,
,
,
,
n- ?
, 30 . , 2
m 2 m ×
m , , . , , , O(
n 2 ) ( ). , O(
n ) ? .
, 1 , , - O(
n ) — , « ». , ( , 2 ), , , .
- , , , ? ,
, .
. «» , , , .
30 - . ( — — 30
Wolfram Language, « !» ).
: «
- , , ». ? , , , - .
. , — , . ,
, , — - «» 30.
,
30. , 30 - . , , , - 30 , , , , — 30, , , , .
. ,
3 2 6 :

CodeRow[Riffle[
ArrayPlot[#, ImageSize -> {Automatic, 275}] & /@ {Table[
IntegerDigits[3^t, 2, 159], {t, 100}],
Table[IntegerDigits[3^t, 6, 62], {t, 100}]}, Spacer[10]]]
, 6
. ( 2 ). , , .
s- n .
s- 3
n , «» (
b — , 2 6)
Mod [
Quotient [3
n , b
s ], b]. ? , 3
n n , : , , 3
n , log(
n ). , ,
, . , 30, , - , .
3
n -
30 , , O(
n ), ,
n , . ,
r [
n ] ,
r [
n ] «O-»
n , ,
MaxLimit [
r [
n ]/
n ,
n →∞ ]<∞.
, ( - ), . ,
r [
n ]
n , , , - , ,
r [
n ]
. , -
n ( - ),
r [
n ] . , , ,
r [
n ] O(
n ).
30
, ( , ).
Wolfram Language
t 30 :
![c[t_] c[t_]](https://habrastorage.org/getpro/habr/post_images/219/e07/f8e/219e07f8ec41111ce3457989e3d3c188.png)
Codec[t_] := CellularAutomaton[30, {{1}, 0}, {t, {{0}}}]
c [
t ].
1: ?

Code\!\(
\*SubscriptBox[\(\[NotExists]\), \({p, i}\)]\(
\*SubscriptBox[\(\[ForAll]\), \(t, t > i\)]c[t + p] == c[t]\)\)

CodeNotExists[{p, i}, ForAll[t, t > i, c[t + p] == c[t]]]
p i t ,
t >
i ,
[
t +
p ]
c [
t ].
2: ?

Code\!\(\*UnderscriptBox[\(\[Limit]\), \(t\*
UnderscriptBox["\[Rule]",
TemplateBox[{},
"Integers"]]\[Infinity]\)]\) Total[c[t]]/t == 1/2

CodeDiscreteLimit[Total[c[t]]/t, t -> Infinity] == 1/2
c [
t ]/
t t →∞ 1/2.
3: n- O( n ) ?
machine[
m ] ,
m (,
TuringMachine [...]), machine[
m ][
n ] {
v ,
t },
v — ,
t — (, ). :
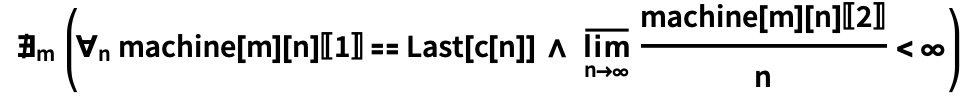
Code\!\(
\*SubscriptBox[\(\[NotExists]\), \(m\)]\((
\*SubscriptBox[\(\[ForAll]\), \(n\)]\(\(machine[m]\)[n]\)[[1]] ==
Last[c[n]]\ \[And] \
\*UnderscriptBox[\(\[MaxLimit]\), \(n -> \[Infinity]\)]
\*FractionBox[\(\(\(machine[m]\)[n]\)[[
2]]\), \(n\)] < \[Infinity])\)\)
« m, , machine[
m ]
n c [
n ] ,
n , ». (
m , «» ).
, , , , . 3 ( ), , 1 2, . 3 ( ), , 1 . :
1 , , 3 .
1 , , , , , 2. , 2 - 3. ,
, O(
n ) — , , 3, , .
, , ?
1 , , , 30 - , . , 1 , . , , - , .
( , ), 2, 3 , — , , , . , 3 , , (, , ), O(
n ) .
, - . ,
n n- . . , - , . , ,
n n . , . , « » . ,
n , . , , O(
n ) .
:
? « »,
/
( ).
, , (
)? , , , , «» , -, ( ) , .
, ,
. , , , . , () .
, , , , : «
». , , , .
, — - . -
n , . . — («
» . .). , , , .
— , , . , (
FindEquationalProof ). , ()
.
,
, , — , . — , .
, .
Wolfram|Alpha (, ) , . , .
, , -
, , , , .
? ,
«» , .
Wolfram Language , . Wolfram Language, .
« »? , , - . . - , , «» , , - ( ), . , , «» — , .
?
, ? . . , . - , . . - , , .
, , «» — , — , « ». ,
2,3 2007 .
— , , 30, , .
. - ( , , ). , , ( ) , , .
n — 30
n ,
n .
Wolfram Language . , 0,4 100 000 :

CodeCellularAutomaton[30, {{1}, 0}, {100000, {{0}}}]; // Timing
,
30 Xor [
p ,
Or [
q ,
r ]],
.
,
CellularAutomaton :

CodeModule[{a = 1},
Table[BitGet[a, a = BitXor[a, BitOr[2 a, 4 a]]; i - 1], {i,
100000}]]; // Timing
.
. , , 30, , 30 , , , : .
. , , «»
. 30 — . , , , .
— , , . , , 30, .
, , 30,
. 45° , 30, , . ; . ?
? ? - ?
, , , , , .
?
30, . , , ,
, ,
. , - , , ,
, , , - .
– , «» .
( , - ). , , , ,
« » :

CodeGraphicsRow[(ArrayPlot[
CellularAutomaton[30,
MapAt[1 - #1 &, Flatten[Table[#1, Round[150/Length[#1]]]], 50],
100]] &) /@ {{1, 0}, {1, 1, 1, 1, 1, 0, 0, 0, 0, 1, 0, 0}, {1,
0, 0, 0, 0, 0, 0}, {1, 1, 1, 0, 0}}]
, , , . ? , « » ?
, (, ), , - 30?
« 30». , «» ? 30 , ? «» ?
, , 30, , , , 30, . 256 ( ) , , :

CodeRow[Riffle[
Labeled[ArrayPlot[CellularAutomaton[#, {{1}, 0}, {150, All}],
PixelConstrained -> 1, Frame -> False],
Style[Text[StringTemplate["rule ``"][#]], 12],
LabelStyle -> Opacity[.5]] & /@ {45, 73}, Spacer[8]]]
, . , . ,
, . , , , « 30», .
« 30». 30 ( 1), , — , .
2, 30, , .
3 .
n- O(
n γ ) γ <2 ( - )? ,
n- , O(log(
n )) ? O(log(
n )) ? ? . ?
, 30. 30, (, , 110) , 30.
, NP-, 30 , , NP-? , . , , , « », 30?
?
2007 2,3 , — , , , . , . 30? Ich weiß nicht. 40 , - ( , !). , , (, ) .
, - ( ), , , , , , , . ( ), , , .
, « » ( , ), . , . , (« » . .). . , - « », , , …
, . , , . , , . , .
, 30 40 , - .
Wolfram Language?
« Wolfram » ( ).