Euler-Poisson-Integral. Details zu Berechnungsmethoden

In dem Artikel werden bis ins kleinste Detail drei Methoden zur Verwendung des Euler-Poisson-Integrals betrachtet. Bei einer der Methoden wird eine Hilfsreduktionsformel abgeleitet. Um einige komplexe Integrale zu finden, kann man Reduktionsformeln verwenden, mit denen man den Grad des Integranden senken und die entsprechenden Integrale in einer endlichen Anzahl von Schritten berechnen kann.

Dieses Integral stammt aus der Gaußschen Funktion: $$$I = \ int \ limit_0 ^ \ infty {e ^ {- x ^ 2} dx}$
Es gibt einen sehr interessanten mathematischen Weg. Um das ursprüngliche Integral zu finden, suchen Sie zuerst nach dem Quadrat dieses Integrals und ziehen Sie dann die Wurzel aus dem Ergebnis. Warum? Ja, weil es so viel einfacher und schmerzloser ist, zu den Polarkoordinaten zu gehen. Betrachten Sie daher das Quadrat des Gaußschen Integrals:
$$$I ^ 2 = \ int \ Limits_0 ^ \ Infty {e ^ {- x ^ 2} dx} \ int \ Limits_0 ^ \ Infty {e ^ {- y ^ 2} dy} = \ int \ Limits_0 ^ \ Infty { \ int \ limit_0 ^ \ infty {e ^ {- \ left ({x ^ 2 + y ^ 2} \ right)}}} dxdy$
Wir sehen, dass wir ein Doppelintegral einer Funktion erhalten $$$g \ left ({x, y} \ right) = \ exp \ left [{- \ left ({x ^ 2 + y ^ 2} \ right)} \ right]$ . Am Ende dieses Oberflächenintegrals befindet sich das Flächenelement im kartesischen Koordinatensystem $$$dS = dxdy$ .
Gehen wir nun zum Polarkoordinatensystem über:

$$

$$\ begin {array} {l} dS = dxdy = rd \ varphi \ cdot dr \\ \ left. \ begin {array} {l} x = r \ cos \ varphi \\ y = r \ sin \ varphi \\ \ end {array} \ right | \ bis x ^ 2 \ cos ^ 2 \ varphi + y ^ 2 \ sin ^ 2 \ varphi = r ^ 2 \ bis x ^ 2 + y ^ 2 = r ^ 2 \\ \ end {array}$$

Hierbei ist zu beachten, dass r von 0 bis + ∞ variieren kann, weil x variierte im gleichen Bereich. Der Winkel φ variiert jedoch von 0 bis π / 2, was den Integrationsbereich im ersten Viertel des kartesischen Koordinatensystems beschreibt. Wenn wir die Quelle einsetzen, erhalten wir:

$$

$$\ begin {array} {l} I ^ 2 = \ int \ border_0 ^ \ infty {\ int \ border_0 ^ \ infty {e ^ {- \ left ({x ^ 2 + y ^ 2} \ right)}} } dxdy = \ int \ limit_0 ^ {\ frac {\ pi} {2}} {\ int \ limit_0 ^ \ infty {e ^ {- r ^ 2}}} rd \ varphi dr = \ int \ limit_0 ^ {\ frac {\ pi} {2}} {d \ varphi} \ int \ limit_0 ^ \ infty {e ^ {- r ^ 2} rdr} = \ int \ limit_0 ^ {\ frac {\ pi} {2}} { d \ varphi} \ int \ limit_0 ^ \ infty {e ^ {- r ^ 2} \ frac {1} {2} d \ left ({r ^ 2} \ right)} = \\ = \ frac {1} {2} \ int \ limit_0 ^ {\ frac {\ pi} {2}} {d \ varphi} \ left ({\ left. {- e ^ {- r ^ 2}} \ right | _0 ^ \ infty} \ right) = \ frac {1} {2} \ int \ border_0 ^ {\ frac {\ pi} {2}} {d \ varphi} \ left ({- e ^ {- \ infty} - \ left ({ - e ^ 0} \ right)} \ right) = \ frac {1} {2} \ int \ border_0 ^ {\ frac {\ pi} {2}} {d \ varphi} = \ frac {1} {2 } \ left ({\ left. \ varphi \ right | _0 ^ {\ frac {\ pi} {2}}} \ right) = \ frac {\ pi} {4} \\ I ^ 2 = \ frac {\ pi} {4} \ to I = \ sqrt {\ frac {\ pi} {4}} = \ frac {{\ sqrt \ pi}} {2} \\ \ end {array}$$

Aufgrund der Symmetrie des Integrals und des positiven Wertebereichs des Integranden können wir daraus schließen

$$

$$\ int \ limit_ {- \ infty} ^ \ infty {e ^ {- x ^ 2} dx} = 2 \ int \ limit_0 ^ \ infty {e ^ {- x ^ 2} dx} = 2 \ cdot \ frac {{\ sqrt \ pi}} {2} = \ sqrt \ pi$$

Lassen Sie uns weitere Lösungen finden? Das ist interessant! :) :)

Betrachten Sie die Funktion $$$g \ left (t \ right) = \ left ({1 + t} \ right) e ^ {- t}$
Erinnern wir uns nun an die Schulmathematik und führen eine einfache Untersuchung einer Funktion unter Verwendung von Ableitungen und Grenzen durch. Es ist nicht so, dass wir hier komplexe Grenzen berücksichtigen (schließlich werden sie in der Schule nicht überschritten), wir diskutieren nur, was mit der Funktion passieren wird, wenn ihr Argument gegen Null oder gegen Unendlich tendiert, und schätzen daher das asymptotische Verhalten, das in der Mathematik immer sehr wichtig ist. Dies ist wie eine qualitative Einschätzung dessen, was passiert.

$$

$$\ begin {array} {l} g \ left (t \ right) = \ left ({1 + t} \ right) e ^ {- t} \\ g '\ left (t \ right) = e ^ { - t} - \ left ({1 + t} \ right) e ^ {- t} = - te ^ {- t} \\ g '\ left (t \ right) = 0 \ bis t = 0 \\ \ left [\ begin {array} {l} t <0 \ to - te ^ {- t}> 0 \ to g \ left (t \ right) - {\ rm {erhöht}} \\ t> 0 \ to - te ^ {- t} <0 \ bis g \ left (t \ right) - {\ rm {verringert}} \\ \ end {array} \ right. \\ g \ left (0 \ right) = \ left ({1 + 0} \ right) e ^ {- 0} = 1 \\ g \ left ({- 1} \ right) = \ left ({1 - 1} \ right) e ^ {- \ left ({- 1} \ right)} = 0 \\ g \ left (\ infty \ right) = \ left ({1 + \ infty} \ right) e ^ {- \ infty} = 0 \\ \ end {array}$$

Es ist oben durch die Einheit im Intervall (-∞; + ∞) und durch Null im Intervall [-1; + ∞) begrenzt.

Wir nehmen die folgende Änderung von Variablen vor $$$t = \ pm x ^ 2$
Und wir bekommen:

$$

$$t = \ pm x ^ 2 \ nach \ left \ {\ begin {array} {l} 0 <\ left ({1 - x ^ 2} \ right) e ^ {x ^ 2} <1 \\ 0 < \ left ({1 + x ^ 2} \ right) e ^ {- x ^ 2} <1 \\ \ end {array} \ right. \ to \ left \ {\ begin {array} {l} 0 <\ left ({1 - x ^ 2} \ right) <e ^ {- x ^ 2} \\ 0 <e ^ {- x ^ 2} <\ frac {1} {{1 + x ^ 2}} \\ \ end {array} \ right.$$

In der ersten Ungleichung beschränken wir die Variation (0,1) und in der zweiten, dem Intervall (0; + ∞), erhöhen wir beide Ungleichungen auf die Potenz n, da Ungleichungen mit positiven Termen in jedem positiven Ausmaß erhöht werden können. Wir bekommen:

$$

$$\ begin {array} {* {20} c} {\ left \ {\ begin {array} {l} \ left ({1 - x ^ 2} \ right) ^ n <e ^ {- nx ^ 2} \\ 0 <x <1 \\ \ end {array} \ right.} & {\ Left \ {\ begin {array} {l} e ^ {- nx ^ 2} <\ frac {1} {{\ left ({1 + x ^ 2} \ right) ^ n}} \\ x> 1 \\ \ end {array} \ right.} \\ \ end {array}$$

Konstruieren wir Graphen für n = 1, um die Ungleichungen zu demonstrieren

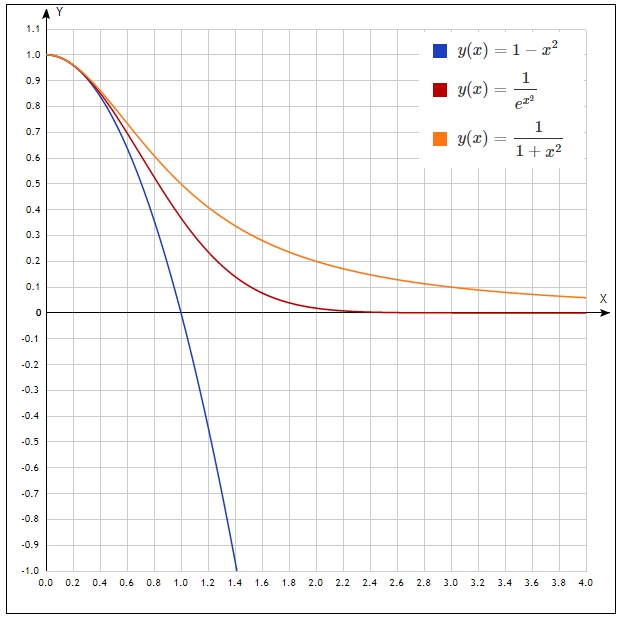
Nun versuchen wir, die Ungleichungen innerhalb der in den entsprechenden Systemen angegebenen Grenzen zu integrieren. Und kombinieren Sie sofort alles zu einer Ungleichung:

$$

$$\ int \ limit_0 ^ 1 {\ left ({1 - x ^ 2} \ right) ^ n dx} <\ int \ limit_0 ^ 1 {e ^ {- nx ^ 2} dx} <\ int \ limit_0 ^ \ infty {e ^ {- nx ^ 2} dx} <\ int \ limit_0 ^ \ infty {\ frac {1} {{\ left ({1 + x ^ 2} \ right) ^ n}} dx}$$

Wenn Sie sich die Grafiken ansehen, ist diese Ungleichung wieder wahr.

Bei einem kleinen Ersatz ist leicht zu erkennen, dass:

$$

$$\ int \ limit_0 ^ \ infty {e ^ {- nx ^ 2} dx} = \ left [\ begin {array} {l} p = \ sqrt nx \\ p ^ 2 = nx ^ 2 \\ \ frac { {dp}} {{\ sqrt n}} = dx \\ \ end {array} \ right] = \ frac {1} {{\ sqrt n}} \ int \ limit_0 ^ \ infty {e ^ {- p ^ 2} dp} = \ frac {1} {{\ sqrt n}} I$$

Das heißt, In dieser großen Ungleichung in der Mitte haben wir das Euler-Poisson-Integral, und jetzt müssen wir die Integrale finden, die an den Grenzen dieser Ungleichung stehen.

Suchen Sie das Integral am linken Rand:

$$

$$\ begin {array} {l} \ int \ border_0 ^ 1 {\ left ({1 - x ^ 2} \ right) ^ n dx} = \ left [{\ begin {array} {* {20} c} \ begin {array} {l} x = \ sin t \\ dx = \ cos tdt \\ 1 - x ^ 2 = 1 - \ sin ^ 2 t = \ cos ^ 2 t \\ \ end {array} & \ begin {array} {l} x = 1 \ bis t = \ arcsin 1 = \ frac {\ pi} {2} \\ x = 0 \ bis t = \ arcsin 0 = 0 \\ \ end {array} \\ \ end {array}} \ right] = \\ = \ int \ limit_0 ^ {\ frac {\ pi} {2}} {\ cos ^ {2n} t \ cdot \ cos tdt} = \ int \ limit_0 ^ { \ frac {\ pi} {2}} {\ cos ^ {2n + 1} tdt} \\ \ end {array}$$

Um es zu berechnen und zu bewerten, finden wir zunächst ein allgemeines Integral. Jetzt werde ich Ihnen zeigen, wie Sie die Reduktionsformel (in der Mathematik bedeuten solche Formeln das Verringern des Grades) für ein bestimmtes Integral ableiten.

$$

$$\ begin {array} {l} \ int \ limit_ \ alpha ^ \ beta {\ cos ^ n tdt} = \ int \ limit_ \ alpha ^ \ beta {\ cos ^ {n - 1} t \ cos tdt} = \ int \ limit_ \ alpha ^ \ beta {\ cos ^ {n - 1} t \ cdot d \ left ({\ sin t} \ right)} = \\ = \ left [{\ begin {array} {* { 20} c} {u = \ cos ^ {n - 1} t} & {du = - \ left ({n - 1} \ right) \ cos ^ {n - 2} t \ sin tdt} \\ {dv = d \ left ({\ sin t} \ right)} & {v = \ sin t} \\ \ end {array}} \ right] = \\ = \ left. {\ cos ^ {n - 1} t \ sin t} \ rechts | _ \ alpha ^ \ beta + \ links ({n - 1} \ rechts) \ int \ limit_ \ alpha ^ \ beta {\ cos ^ {n - 2} t \ sin ^ 2 tdt} = \\ = \ left. {\ cos ^ {n - 1} t \ sin t} \ rechts | _ \ alpha ^ \ beta + \ links ({n - 1} \ rechts) \ int \ limit_ \ alpha ^ \ beta {\ cos ^ {n - 2} t \ left ({1 - \ cos ^ 2 t} \ right) dt} = \\ = \ left. {\ cos ^ {n - 1} t \ sin t} \ rechts | _ \ alpha ^ \ beta + \ links ({n - 1} \ rechts) \ int \ limit_ \ alpha ^ \ beta {\ cos ^ {n - 2} tdt} - \ left ({n - 1} \ right) \ int \ limit_ \ alpha ^ \ beta {\ cos ^ n tdt} \\ \ end {array}$$

$$

$$\ begin {array} {l} \ int \ limit_ \ alpha ^ \ beta {\ cos ^ n tdt} = \ left. {\ cos ^ {n - 1} t \ sin t} \ rechts | _ \ alpha ^ \ beta + \ links ({n - 1} \ rechts) \ int \ limit_ \ alpha ^ \ beta {\ cos ^ {n - 2} tdt} - \ left ({n - 1} \ right) \ int \ limit_ \ alpha ^ \ beta {\ cos ^ n tdt} \\ \ int \ border_ \ alpha ^ \ beta {\ cos ^ n tdt } + \ left ({n - 1} \ right) \ int \ border_ \ alpha ^ \ beta {\ cos ^ n tdt} = \ left. {\ cos ^ {n - 1} t \ sin t} \ rechts | _ \ alpha ^ \ beta + \ links ({n - 1} \ rechts) \ int \ limit_ \ alpha ^ \ beta {\ cos ^ {n - 2} tdt} \\ n \ int \ limit_ \ alpha ^ \ beta {\ cos ^ n tdt = \ left. {\ cos ^ {n - 1} t \ sin t} \ rechts | _ \ alpha ^ \ beta + \ links ({n - 1} \ rechts) \ int \ limit_ \ alpha ^ \ beta {\ cos ^ {n - 2} tdt}} \\ \ int \ limit_ \ alpha ^ \ beta {\ cos ^ n tdt = \ frac {1} {n} \ left. {\ cos ^ {n - 1} t \ sin t} \ right | _ \ alpha ^ \ beta + \ frac {{n - 1}} {n} \ int \ limit_ \ alpha ^ \ beta {\ cos ^ { n - 2} tdt}} \\ \ end {array}$$

Wenn wir nun die Reduktionsformel verwenden, betrachten wir dasselbe Integral, aber mit unseren Grenzen von 0 bis π / 2, können wir einige Vereinfachungen vornehmen:

$$

$$\ begin {array} {l} \ int \ border_0 ^ {\ frac {\ pi} {2}} {\ cos ^ n tdt = \ frac {1} {n} \ left. {\ cos ^ {n - 1} t \ sin t} \ right | _0 ^ {\ frac {\ pi} {2}} + \ frac {{n - 1}} {n} \ int \ border_0 ^ {\ frac {\ pi} {2}} {\ cos ^ {n - 2} tdt}} = \ left [{\ frac {1} {n} \ left. {\ cos ^ {n - 1} t \ sin t} \ right | _0 ^ {\ frac {\ pi} {2}} = 0} \ right] = \\ = \ frac {{n - 1}} { n} \ int \ limit_0 ^ {\ frac {\ pi} {2}} {\ cos ^ {n - 2} tdt} = \ frac {{n - 1}} {n} \ left ({\ frac {1 } {{n - 2}} \ left. {\ cos ^ {n - 3} t \ sin t} \ right | _0 ^ {\ frac {\ pi} {2}} + \ frac {{n - 3} } {{n - 2}} \ int \ border_0 ^ {\ frac {\ pi} {2}} {\ cos ^ {n - 4} tdt}} \ right) = \\ = \ frac {{n - 1 }} {n} \ left ({\ frac {{n - 3}} {{n - 2}} \ int \ border_0 ^ {\ frac {\ pi} {2}} {\ cos ^ {n - 4} tdt}} \ right) = \ frac {{n - 1}} {n} \ left ({\ frac {{n - 3}} {{n - 2}} \ left ({\ frac {{n - 5) }} {{n - 4}} \ int \ border_0 ^ {\ frac {\ pi} {2}} {\ cos ^ {n - 6} tdt}} \ right)} \ right) = \\ = \ frac {{n - 1}} {n} \ left ({\ frac {{n - 3}} {{n - 2}} \ left ({\ frac {{n - 5}} {{n - 4}} \ left ({\ frac {{n - 7}} {{n - 6}} \ int \ border_0 ^ {\ frac {\ pi} {2}} {\ cos ^ {n - 8} tdt}} \ right )} \ right)} \ right) = ... \\ \ end {array}$$

Wie wir sehen, können Sie es auf unendlich senken (hängt von n ab). Es gibt jedoch eine Subtilität. Die Formel ändert sich abhängig davon, ob n eine gerade Zahl ist oder nicht.
Hierzu betrachten wir zwei Fälle.

$$

$$\ begin {array} {l} n = 10: \\ \ int \ border_0 ^ {\ frac {\ pi} {2}} {\ cos ^ {10} tdt} = \ frac {{9 \ cdot 7 \ cdot 5 \ cdot 3}} {{10 \ cdot 8 \ cdot 6 \ cdot 4}} \ int \ limit_0 ^ {\ frac {\ pi} {2}} {\ cos ^ 2 tdt} = \ frac {{9 \ cdot 7 \ cdot 5 \ cdot 3}} {{10 \ cdot 8 \ cdot 6 \ cdot 4}} \ int \ limit_0 ^ {\ frac {\ pi} {2}} {\ left ({\ frac {1 } {2} + \ frac {1} {2} \ cos 2t} \ right) dt} = \\ = \ frac {{9 \ cdot 7 \ cdot 5 \ cdot 3}} {{10 \ cdot 8 \ cdot 6 \ cdot 4}} \ left. {\ left ({\ frac {1} {2} t + \ frac {1} {2} \ sin 2t} \ right)} \ right | _0 ^ {\ frac {\ pi} {2}} = \ frac {{9 \ cdot 7 \ cdot 5 \ cdot 3}} {{10 \ cdot 8 \ cdot 6 \ cdot 4}} \ cdot \ frac {\ pi} {4} = \ frac {{9 \ cdot 7 \ cdot 5 \ cdot 3 \ cdot 1}} {{10 \ cdot 8 \ cdot 6 \ cdot 4 \ cdot 2}} \ cdot \ frac {\ pi} {2} = \\ = \ frac {{\ left ({n - 1} \ right) !!}} {{n !!}} \ cdot \ frac {\ pi} {2} \\ \ end {array}$$

$$

$$\ begin {array} {l} n = 9: \\ \ int \ limit_0 ^ {\ frac {\ pi} {2}} {\ cos ^ 9 tdt} = \ frac {{8 \ cdot 6 \ cdot 4 \ cdot 2}} {{9 \ cdot 7 \ cdot 5 \ cdot 3}} \ int \ limit_0 ^ {\ frac {\ pi} {2}} {\ cos tdt} = \ frac {{8 \ cdot 6 \ cdot 4 \ cdot 2}} {{9 \ cdot 7 \ cdot 5 \ cdot 3}} übrig. {\ left ({\ sint} \ right)} \ right | _0 ^ {\ frac {\ pi} {2}} = \\ = \ frac {{8 \ cdot 6 \ cdot 4 \ cdot 2}} { {9 \ cdot 7 \ cdot 5 \ cdot 3 \ cdot 1}} = \ frac {{\ left ({n - 1} \ right) !!}} {{n !!}} \\ \ end {array}$$

Wo ist n !! - doppelte Fakultät. Die doppelte Fakultät von n wird mit n bezeichnet !! und ist definiert als das Produkt aller natürlichen Zahlen im Intervall [1, n] mit der gleichen Parität wie n

Aufgrund der Tatsache, dass 2n + 1 eine ungerade Zahl für jeden Wert von n ist, erhalten wir für die linke Grenze unserer Ungleichung:

$$

$$\ int \ limit_0 ^ {\ frac {\ pi} {2}} {\ cos ^ {2n + 1} tdt} = \ frac {{\ left ({2n} \ right) !!}} {{\ left ({2n + 1} \ right) !!}}$$

Suchen Sie das Integral am rechten Rand:
(hier verwenden wir die gleiche Reduktionsformel, die zuvor bewiesen wurde)

$$

$$\ begin {array} {l} \ int \ border_0 ^ \ infty {\ frac {1} {{\ left ({1 + x ^ 2} \ right) ^ n}} dx = \ left [\ begin {array } {l} x = \ tan t \ to \ begin {array} {* {20} c} {x = 0 \ to t = 0} \\ {x = \ infty \ to t = \ frac {\ pi} {2}} \\ \ end {array} \\ dx = \ frac {{dt}} {{\ cos ^ 2 t}} \\ \ frac {1} {{1 + x ^ 2}} = \ frac {1} {{1 + \ tan ^ 2 t}} = \ cos ^ 2 t \\ \ end {array} \ right]} = \\ = \ int \ limit_0 ^ {\ frac {\ pi} {2} } {\ cos ^ {2n - 2} tdt} = \ left [{\ left ({2n - 2} \ right) - {\ rm {even}}} right] = \ frac {{\ left ({2n - 3} \ right) !!}} {{\ left ({2n - 2} \ right) !!}} \ cdot \ frac {\ pi} {2} \\ \ end {array}$$

Nachdem wir die linke und rechte Seite der Ungleichung geschätzt haben, führen wir einige Transformationen durch, um die Grenzen der linken und rechten Seite der Ungleichung zu bewerten, vorausgesetzt, n tendiert zu ∞:

$$

$$\ begin {array} {l} \ frac {{\ left ({2n} \ right) !!}} {{\ left ({2n + 1} \ right) !!}} <\ frac {1} { {\ sqrt n}} \ cdot I <\ frac {{\ left ({2n - 3} \ right) !!}} {{\ left ({2n - 2} \ right) !!}} \ cdot \ frac {\ pi} {2} \\ \ sqrt n \ cdot \ frac {{\ left ({2n} \ right) !!}} {{\ left ({2n + 1} \ right) !!}} <I <\ sqrt n \ cdot \ frac {{\ left ({2n - 3} \ right) !!}} {{\ left ({2n - 2} \ right) !!}} \ cdot \ frac {\ pi} {2} \\ \ end {array}$$

Quadrieren Sie beide Seiten der Ungleichung:

$$

$$n \ cdot \ frac {{\ left ({\ left ({2n} \ right) !!} \ right) ^ 2}} {{\ left ({\ left ({2n + 1} \ right) !! } \ right) ^ 2}} <I ^ 2 <n \ cdot \ frac {{\ left ({\ left ({2n - 3} \ right) !!} \ right) ^ 2}} {{\ left ( {\ left ({2n - 2} \ right) !!} \ right) ^ 2}} \ cdot \ frac {{\ pi ^ 2}} {4}$$

Jetzt machen wir einen kleinen Exkurs. 1655 schlug John Wallis (ein englischer Mathematiker, einer der Vorläufer der mathematischen Analyse) eine Formel zur Bestimmung der Zahl π vor. J. Wallis kam zu ihr und berechnete die Fläche eines Kreises. Dieses Produkt konvergiert extrem langsam, daher ist die Wallis-Formel für die praktische Berechnung der Zahl π von geringem Nutzen. Aber um unseren Ausdruck zu bewerten, ist es großartig :)

$$

$$\ pi = \ mathop {\ lim} \ limit_ {n \ to \ infty} \ frac {1} {n} \ left [{\ frac {{\ left ({2n} \ right) !!}} {{ \ left ({2n - 1} \ right) !!}}} \ right] ^ 2$$

Jetzt transformieren wir unsere Ungleichung, damit wir sehen können, wo die Wallis-Formel ersetzt werden kann:

$$

$$\ begin {array} {l} \ frac {{n ^ 2}} {{\ left ({2n + 1} \ right) ^ 2}} \ cdot \ frac {1} {n} \ cdot \ frac { {\ left ({\ left ({2n} \ right) !!} \ right) ^ 2}} {{\ left ({\ left ({2n - 1} \ right) !!} \ right) ^ 2} } <I ^ 2 <\ frac {1} {{\ frac {1} {n} \ cdot \ frac {{\ left ({\ left ({2n - 2} \ right) !!} \ right) ^ 2 }} {{\ left ({\ left ({2n - 3} \ right) !!} \ right) ^ 2}}} \ cdot \ frac {{\ pi ^ 2}} {4} \\ \ mathop {\ lim} \ limit_ {n \ to \ infty} \ left [{\ frac {{n ^ 2}} {{\ left ({2n + 1} \ right) ^ 2}}} \ right] \ cdot \ mathop {\ lim} \ limit_ {n \ to \ infty} \ left [{\ frac {1} {n} \ cdot \ frac {{\ left ({\ left ({2n} \ right) !!} \ right ) ^ 2}} {{\ left ({\ left ({2n - 1} \ right) !!} \ right) ^ 2}}} \ right] <I ^ 2 <\ frac {1} {{\ mathop {\ lim} \ limit_ {n \ to \ infty} \ left [{\ frac {1} {n} \ cdot \ frac {{\ left ({\ left ({2n - 2} \ right) !!} \ rechts) ^ 2}} {{\ left ({\ left ({2n - 3} \ right) !!} \ right) ^ 2}}} \ right]}} \ cdot \ frac {{\ pi ^ 2} } {4} \\ \ frac {1} {4} \ cdot \ pi <I ^ 2 <\ frac {1} {\ pi} \ cdot \ frac {{\ pi ^ 2}} {4} \ to \ frac {\ pi} {4} <I ^ 2 <\ frac {\ pi} {4} \\ I ^ 2 = \ frac {\ pi} {4} \ to I = \ frac {{\ sqrt \ pi}} {2} \\ \ end {array}$$

Aus der Wallis-Formel folgt, dass sowohl der linke als auch der rechte Ausdruck zu π / 4 als n → ∞ tendieren
Aufgrund der Tatsache, dass die Funktion exp [-x²] gerade ist, gehen wir davon aus

$$

$$\ int \ limit_ {- \ infty} ^ \ infty {e ^ {- x ^ 2} dx} = 2 \ int \ limit_0 ^ \ infty {e ^ {- x ^ 2} dx} = 2 \ cdot \ frac {{\ sqrt \ pi}} {2} = \ sqrt \ pi$$

Zum ersten Mal wurde das eindimensionale Gaußsche Integral 1729 von Euler berechnet, dann fand Poisson einen einfachen Weg, es zu berechnen. In dieser Hinsicht wurde es das Euler-Poisson-Integral genannt.

Versuchen wir, das Gaußsche Integral zu berechnen. Es kann in verschiedenen Formen geschrieben werden. Schließlich ändert nichts den Namen der Variablen, unter der die Integration stattfindet.

$$

$$\ begin {array} {l} I = \ int \ border_0 ^ \ infty {e ^ {- x ^ 2} dx} \\ I = \ int \ border_ {- \ infty} ^ \ infty {e ^ {- x ^ 2} dx} = \ int \ Grenzen_ {- \ Infty} ^ \ Infty {e ^ {- y ^ 2} dy} = \ int \ Grenzen_ {- \ Infty} ^ \ Infty {e ^ {- z ^ 2} dz} \\ \ end {array}$$

Sie können von dreidimensionalen kartesischen zu sphärischen Koordinaten wechseln und den Würfel des Gauß-Integrals betrachten.

$$

$$\ left \ {\ begin {array} {l} x = r \ sin \ theta \ cos \ varphi \\ y = r \ sin \ theta \ sin \ varphi \\ z = r \ cos \ theta \\ \ end {array} \ right. \ bis x ^ 2 + y ^ 2 + z ^ 2 = r ^ 2$$

Der Jacobi dieser Transformation kann wie folgt berechnet werden:

$$

$$\ begin {array} {l} J = \ left | {\ begin {array} {* {20} c} {\ frac {{\ partielle x}} {{\ partielle r}}} & {\ frac {{\ partielle x}} {{\ partielle \ theta}} } & {\ frac {{\ partielles x}} {{\ partielles \ varphi}} \\ {\ frac {{\ partielles y}} {{\ partielles r}}} & {\ frac {{\ partielles y }} {{\ partielle \ theta}}} & {\ frac {{\ partielle y}} {{\ partielle \ varphi}}} \\ {\ frac {{\ partielle z}} {{\ partielle r}} } & {\ frac {{\ partielles z}} {{\ partielles \ theta}} & {\ frac {{\ partielles z}} {{\ partielles \ varphi}} \\ \ end {array}} \ rechts | = \ left | {\ begin {array} {* {20} c} {\ sin \ theta \ cos \ varphi} & {r \ cos \ theta \ cos \ varphi} & {- r \ sin \ theta \ sin \ varphi} \\ {\ sin \ theta \ sin \ varphi} & {r \ cos \ theta \ sin \ varphi} & {r \ sin \ theta \ cos \ varphi} \\ {r \ cos \ theta} & {- r \ sin \ Theta} & 0 \\ \ end {array}} \ right | = \\ = r ^ 2 \ sin \ theta \\ \ end {array}$$

$$

$$\ begin {array} {l} I ^ 3 = \ int \ Limits_ {- \ Infty} ^ \ Infty {\ int \ Limits_ {- \ Infty} ^ \ Infty {\ Int \ Limits_ {- \ Infty} ^ \ infty {e ^ {- x ^ 2 - y ^ 2 - z ^ 2}} dxdydz}} = \ int \ limit_0 ^ {2 \ pi} {\ int \ limit_0 ^ \ pi {\ int \ limit_0 ^ \ infty { e ^ {- r ^ 2} Jdrd \ theta d} \ varphi =}} \\ = \ int \ begrenzt_0 ^ {2 \ pi} {d \ varphi} \ int \ Grenzen_0 ^ \ pi {\ sin \ theta d \ theta} \ int \ limit_0 ^ \ infty {e ^ {- r ^ 2} r ^ 2 dr} \\ \ end {array}$$

Wir berechnen die Integrale nacheinander, beginnend mit dem inneren.

$$

$$\ begin {array} {l} \ int \ border_0 ^ \ infty {e ^ {- r ^ 2} r ^ 2 dr} = \ left [\ begin {array} {l} u = r \ to du = dr \\ dv = re ^ {- r ^ 2} dr \ bis v = \ int {re ^ {- r ^ 2} dr} = \ frac {1} {2} \ int {e ^ {- r ^ 2} dr ^ 2} = - \ frac {1} {2} e ^ {- r ^ 2} \\ \ end {array} \ right] = \\ = \ left. {\ left ({- \ frac {1} {2} re ^ {- r ^ 2}} \ right)} \ right | _0 ^ \ infty + \ frac {1} {2} \ int \ limit_0 ^ \ infty {e ^ {- r ^ 2} dr} = \ frac {1} {2} \ int \ limit_0 ^ \ infty {e ^ {- r ^ 2} dr} = \ frac {1} {2} \ cdot \ frac {I} {2} = \ frac {I} {4} \\ \ int \ limit_0 ^ \ pi {\ sin \ theta d \ theta} = \ left. {\ left ({- \ cos \ theta} \ right)} \ right | _0 ^ \ pi = \ left ({- \ cos \ pi} \ right) - \ left ({- \ cos 0} \ right) = 1 + 1 = 2 \\ \ int \ limit_0 ^ {2 \ pi} {d \ varphi} = \ left. \ varphi \ right | _0 ^ {2 \ pi} = 2 \ pi \\ \ end {array}$$

Dann erhalten wir als Ergebnis:

$$

$$\ begin {array} {l} I ^ 3 = 2 \ pi \ cdot 2 \ cdot \ frac {I} {4} \ bis I ^ 3 = \ pi I \ bis I ^ 2 = \ pi \ bis I = \ sqrt \ pi \\ I = \ int \ limit_ {- \ infty} ^ \ infty {e ^ {- x ^ 2} dx} = \ sqrt \ pi \\ \ end {array}$$

Das Euler-Poisson-Integral wird häufig in der Wahrscheinlichkeitstheorie verwendet.

Ich hoffe, dass der Artikel für jemanden nützlich ist und hilft, einige mathematische Techniken zu verstehen :)