Was ein Voltmeter zeigt, oder Mathe-Steckdosen

Worum geht es in diesem Artikel?

Heute werde ich kurz von meinem üblichen Thema der visuellen Programmierung von Steuerungen abweichen und mich dem Thema Spannungsmessungen direkt in der Steckdose zuwenden!

Dieser Artikel entstand aus Diskussionen beim Tee, als unter „allwissenden und allwissenden“ Programmierern eine Debatte darüber ausbrach, was viele von ihnen nicht verstehen, nämlich wie die Spannung in der Steckdose gemessen wird, die ein Wechselspannungsmessgerät zeigt, was die Spitzen- und tatsächlichen Spannungswerte unterscheidet .

Dieser Artikel wird höchstwahrscheinlich für diejenigen interessant sein, die mit der Erstellung ihrer Geräte beginnen. Aber vielleicht hilft es jemandem, der Erfahrung hat, sein Gedächtnis aufzufrischen.

Der Artikel spricht darüber, welche Spannungen im Wechselstromnetz vorhanden sind, wie sie gemessen werden und worauf beim Entwurf elektronischer Schaltungen zu achten ist.
Allen wurde eine kurze und vereinfachte mathematische Begründung gegeben, damit nicht nur klar ist, wie, sondern auch warum.

Wer nicht daran interessiert ist, über Integrale, GOSTs und Phasen zu lesen, kann direkt zum Schluss kommen.

Eintrag

Wenn Leute über die Spannung in der Steckdose sprechen, verbirgt das Stereotyp „in der 220-V-Steckdose“ sehr oft den tatsächlichen Zustand vor ihren Augen.

Zunächst sollte gemäß GOST 29322-2014 die Netzspannung 230 V ± 10% bei einer Frequenz von 50 ± 0,2 Hz betragen (Phase-zu-Phase-Spannung 400 V, phasenneutrale Spannung 230 V). Im selben GOST gibt es jedoch einen Hinweis: "Es werden jedoch weiterhin 220/380-V- und 240/415-V-Systeme verwendet ."

Stimmen Sie zu, dass dies nicht die gleiche eindeutige „ in der 220-V-Steckdose “ ist, die wir gewohnt sind. Und wenn es um „ Phasen “ -, „ lineare “, „ wirkende “ und „ Spitzenspannungen “ geht, ist der Brei im Allgemeinen bemerkenswert. Wie viele Volt sind in der Steckdose?

Um diese Frage zu beantworten, beginnen wir mit der Messung der Wechselspannung.

Wie misst man Wechselspannung?

Bevor wir uns mit dem Dschungel der Wechselstrom- und Spannungskreise befassen, erinnern wir uns an die Schulphysik der Gleichstromkreise.

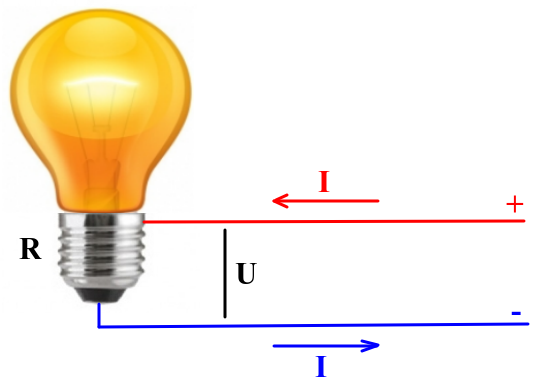
Gleichstromkreise sind eine einfache Sache. Wenn wir eine aktive Last (sei es eine gewöhnliche Glühlampe, wie in der Abbildung) nehmen und an einen Gleichstromkreis anschließen, wird alles, was in unserem Stromkreis passiert, nur durch zwei Größen charakterisiert: die Spannung an der Last U und den durch die Last fließenden Strom I. Die von der Last verbrauchte Leistung wird nach einer aus der Schule bekannten Formel eindeutig berechnet: $$$P = U \ cdot I$ .



Oder angesichts des Ohmschen Gesetzes $$$I = {U \ over R}$ dann kann die von der Glühbirne verbrauchte Leistung P nach der Formel berechnet werden $$$P = {U ^ 2 \ über R}$ .

Bei Wechselspannung ist alles viel komplizierter: Zu jedem Zeitpunkt kann es unterschiedliche Momentanwerte geben. Daher wird zu unterschiedlichen Zeiten an der Last, die an eine Wechselspannungsquelle angeschlossen ist (z. B. an einer Glühlampe, die an eine Steckdose angeschlossen ist), unterschiedliche Leistung freigesetzt. Dies ist im Hinblick auf die Beschreibung des Stromkreises sehr unpraktisch.

Aber wir hatten Glück: Die Spannungsform in der Buchse ist sinusförmig. Wie Sie wissen, wird eine Sinuswelle vollständig durch drei Parameter beschrieben: Amplitude, Periode und Phase. In einphasigen Netzwerken (und ein gewöhnlicher Sockel mit zwei Löchern ist genau ein einphasiges Netzwerk) können Sie die Phase vergessen. Die Abbildung zeigt im Detail zwei Perioden einer einphasigen Netzspannung. Das gleiche in der Steckdose.



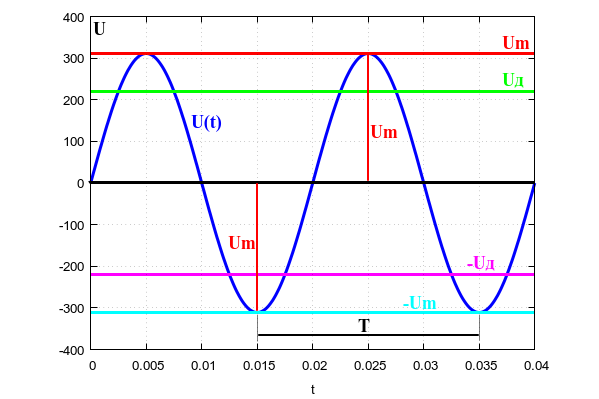
Überlegen Sie, was all diese Buchstaben auf dem Bild bedeuten.

Die Periode T ist die Zeit zwischen zwei benachbarten Minima oder benachbarten Maxima der Sinuswelle. Für das HF-Beleuchtungsnetz beträgt diese Periode 20 Millisekunden , was einer Frequenz von 50 Hz entspricht . Die Frequenz der Spannungsschwankungen des Stromnetzes wird sehr genau auf einen Bruchteil eines Prozent gehalten.

Offensichtlich sind an zwei beliebigen Punkten der Sinuskurve, die durch eine ganzzahlige Anzahl von Perioden voneinander getrennt sind, die Spannungen immer gleich.

Die Amplitude Um ist die maximale Spannung, die Spitze der Sinuskurve. Wir werden über die Stromspannung Ud etwas niedriger sprechen.

Die Spannung in der Steckdose (oder im einphasigen Netzwerk) wird durch die Formel beschrieben

$$

$$U (t) = U_m \ cdot sin (2 \ cdot \ pi \ cdot {t \ over T});$$

Dabei ist t die aktuelle Zeit, Um die Amplitude (oder der Spitzenwert) der Spannung, T die Periode der Netzspannung.

Wenn bei einer einphasigen Wechselspannung alles mehr oder weniger klar ist, werden wir versuchen, die Leistung zu berechnen, die an unserer bevorzugten Glühlampe abgegeben wird, wenn diese direkt an eine Steckdose angeschlossen wird.

Da eine Glühlampe eine aktive Last ist (was bedeutet, dass ihr Widerstand nicht von der Frequenz von Spannung und Strom abhängt), wird die Momentanleistung einer Glühlampe, die an eine Steckdose angeschlossen ist, nach der Formel berechnet

$$

$$P (t) = U (t) \ cdot I (t) = {U ^ 2 (t) \ über R};$$

Dabei ist t die aktuelle Zeit und R der Widerstand der Glühlampe mit einer beheizten Spirale. Wenn wir die Amplitude der Wechselspannung Um kennen , können wir schreiben:

$$

$$P (t) = {{(U_m \ cdot sin (2 \ cdot \ pi \ cdot {t \ über T})) ^ 2} \ über R}$$

Es ist klar, dass die momentane Leistung ein unbequemer Parameter ist und in der Praxis nicht besonders notwendig ist. Daher wird normalerweise die über einen Zeitraum gemittelte Leistung verwendet.
Dies ist die durchschnittliche Leistung, die für Glühbirnen, Heizungen und andere Haushaltsbügeleisen angegeben wird.

Die Durchschnittsleistung wird im allgemeinen Fall nach folgender Formel berechnet:

$$

$$P_ {cp} = {1 \ über {R \ cdot T}} \ cdot \ int_0 ^ T {U ^ 2 (t)} dt$$

Und für unsere Sinuskurve - nach einer viel einfacheren Formel:

$$

$$P_ {cp} = {{U_m ^ 2} \ über {2 \ cdot R}}$$

Sie können ersetzen $$$U (t)$ die Funktion $$$U_m \ cdot sin (2 \ cdot \ pi \ cdot {t \ over T})$ und nimm das Integral, wenn du es nicht glaubst.

Denken Sie nicht an Macht, an die ich mich einfach so erinnerte, aus Schaden. Jetzt wirst du verstehen, warum wir sie brauchten. Wir kommen zur nächsten Frage.

Was zeigt das Voltmeter?

Bei Gleichstromkreisen ist hier alles klar - das Voltmeter zeigt die einzige Spannung zwischen den beiden Kontakten an.

Mit Wechselstromkreisen ist alles wieder komplizierter. Einige (und einige von ihnen sind nicht so wenige, wie ich überzeugt war) glauben, dass das Voltmeter den Spitzenwert der Spannung Um anzeigt, aber das ist nicht so !

In der Tat zeigen Voltmeter normalerweise die effektive oder effektive Spannung, es ist auch die Effektivspannung im Netzwerk Ud .

Natürlich sprechen wir über Wechselspannungsmesser ! Wenn Sie die Netzwerkspannung mit einem Voltmeter messen, stellen Sie daher sicher, dass sie sich im Wechselspannungsmessmodus befindet .

Ich werde reservieren, dass es auch „Spitzenspannungsmesser“ gibt, die die Amplitudenwerte der Spannung anzeigen, aber in der Praxis werden sie bei der Messung der Netzspannung im Alltag normalerweise nicht verwendet.

Wir werden verstehen, warum solche Schwierigkeiten. Warum nicht einfach die Amplitude messen? Warum haben sie sich einen „effektiven Wert“ der Spannung ausgedacht?

Und alles dreht sich um den Stromverbrauch. Ich habe nicht nur über sie geschrieben. Tatsache ist, dass der effektive (effektive) Wert der Wechselspannung gleich der Größe einer solchen konstanten Spannung ist, die in einer Zeit, die einer Periode dieser Wechselspannung entspricht, die gleiche Arbeit wie die betrachtete Wechselspannung leistet .

Oder auf einfache Weise leuchtet das Glühlicht gleich hell, unabhängig davon, ob wir es an ein 220-V- Gleichstromnetz oder an einen Wechselstromkreis mit einem effektiven Spannungswert von 220 V anschließen .

Für diejenigen, die bereits mit den Integralen vertraut sind oder die Mathematik nicht vergessen haben, werde ich eine allgemeine Formel zur Berechnung der effektiven Spannung einer beliebigen Form geben:

$$

$$U_d = \ sqrt {{1 \ über T} \ cdot \ int_0 ^ T {U ^ 2 (t)} dt}$$

Aus dieser Formel wird auch deutlich, warum der effektive (effektive) Wert der Wechselspannung auch als "Effektivwert" bezeichnet wird.

Beachten Sie, dass der radikale Ausdruck dieselbe „über einen Zeitraum gemittelte Leistung“ ist. Sie müssen diesen Ausdruck nur durch den Lastwiderstand R dividieren .

In Bezug auf die sinusförmige Form der Spannung wird das schreckliche Integral nach einfachen Transformationen zu einer einfachen Formel:

$$

$$U_d = {U_m \ over \ sqrt 2}$$

Dabei ist Ud der effektive oder Effektivspannungswert (der gleiche wie der Voltmeter normalerweise zeigt) und Um der Amplitudenwert.

Die effektive Spannung ist gut, da bei einer aktiven Last die Berechnung der Durchschnittsleistung vollständig mit der Berechnung der Gleichstromleistung übereinstimmt:

$$

$$P_ {cp} = {U_m ^ 2 \ über {2 \ cdot R}} = {U_d ^ 2 \ über R}$$

Dies ist nicht überraschend, wenn wir uns an die Definition des effektiven Spannungswerts erinnern, die etwas höher angegeben wurde.

Nun, zum Schluss berechnen wir die Amplitude der Spannung in der Steckdose " 220V ":

$$

$$U_m = U_d \ cdot \ sqrt 2 \ ca. 220B \ cdot 1,41 = 310,2B$$

Im schlimmsten Fall, wenn Sie ein 240-V-Netzwerk haben und sogar mit einer Toleranz von + 10%, ist die Amplitude genauso groß $$$U_m = (240B + 10 \%) \ cdot 1.41 \ ca. 373B$ !

Wenn Sie möchten, dass Ihre vom Netzwerk gespeisten Geräte stabil arbeiten und nicht durchbrennen, wählen Sie daher Elemente, die Spitzenspannungen von mindestens 400 V standhalten. Natürlich handelt es sich um Elemente, die direkt mit Netzspannung versorgt werden.

Ich stelle fest, dass für eine nicht sinusförmige Wellenform der effektive Spannungswert unter Verwendung anderer Formeln berechnet wird. Wen kümmert es - sie können die Integrale selbst übernehmen oder sich an Verzeichnisse wenden. Wir interessieren uns für das Versorgungsnetz, und es sollte immer eine Sinuskurve geben.

Phasen, Phasen, Phasen ...

Neben dem üblichen einphasigen Beleuchtungsnetz ~ 220V hat jeder von dem dreiphasigen Netz ~ 380V gehört . Was ist 380V ? Und dies ist eine effektive Interphasenspannung .

Denken Sie daran, ich sagte, dass Sie in einem einphasigen Netzwerk die Phase einer Sinuskurve vergessen können? In einem dreiphasigen Netzwerk ist dies also nicht möglich!

In einfachen Worten ist die Phase eine Zeitverschiebung einer Sinuskurve relativ zu einer anderen. In einem einphasigen Netzwerk konnten wir immer einen beliebigen Zeitpunkt als Referenzpunkt verwenden - dies hatte keinen Einfluss auf die Berechnungen. In einem dreiphasigen Netzwerk muss berücksichtigt werden, wie weit eine Sinuskurve von der anderen beabstandet ist. In dreiphasigen Wechselstromnetzen ist jede Phase um ein Drittel der Periode oder 120 Grad voneinander getrennt. Ich möchte Sie daran erinnern, dass die Periode auch in Grad gemessen wird und die gesamte Periode 360 Grad beträgt.

Wenn wir ein Oszilloskop mit drei Strahlen nehmen und an drei Phasen und eine Null angeschlossen sind, sehen wir ein solches Bild.



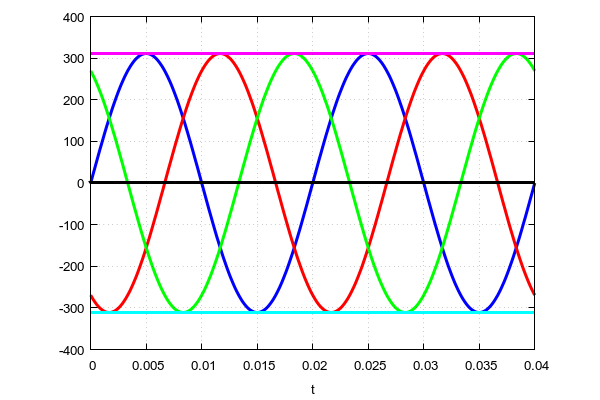
" Blaue " Phase - beginnt bei Null. Die " rote " Phase ist ein Drittel der Periode ( 120 Grad) später. Und schließlich beginnt die „ grüne “ Phase zwei Drittel der Periode ( 240 Grad) später als die „ blaue “ Phase. Alle Phasen sind absolut symmetrisch zueinander.

Welche Phase als Bezugspunkt genommen werden soll, ist nicht wichtig. Das Bild wird das gleiche sein.

Mathematisch können wir die Gleichungen aller drei Phasen schreiben:

Blaue Phase: $$$P (t) = U_m \ cdot sin (2 \ cdot \ pi \ cdot {t \ über T} - 0)$

" Rote " Phase: $$$P (t) = U_m \ cdot sin (2 \ cdot \ pi \ cdot {t \ über T} - {{2 \ über 3} \ cdot \ pi})$

Grüne Phase: $$$P (t) = U_m \ cdot sin (2 \ cdot \ pi \ cdot {t \ über T} - {{4 \ über 3} \ cdot \ pi})$

Wenn Sie die Spannung zwischen einer der Phasen und Null in einem dreiphasigen Netzwerk messen, erhalten wir die üblichen 220 V (oder 230 V oder 240 V - wie es das Glück wollte, siehe GOST ).

Und wenn Sie die Spannung zwischen den beiden Phasen messen - dann erhalten wir 380 V (oder 400 V oder 415 V - vergessen Sie es nicht).

Das heißt, ein dreiphasiges Netzwerk ist vielfältig. Es kann als drei einphasige Netze mit einer Spannung von 220 V oder als ein dreiphasiges Netz mit einer Spannung von 380 V verwendet werden.

Woher kamen 380V ? Aber woher.

Wenn wir unsere Daten für zwei Phasen in die Formel zur Berechnung der effektiven Spannung einsetzen, erhalten wir:

$$

$$U_ {df} = \ sqrt {{U_m ^ 2 \ über T} \ cdot \ int_0 ^ T ({{sin (2 \ cdot \ pi \ cdot {t \ über T} - 0) - sin (2 \ cdot \ pi \ cdot {t \ over T} - {2 \ over 3} \ cdot \ pi)}}) ^ 2 dt}$$

oder vereinfachend:

$$

$$U_ {df} = U_m \ cdot {\ sqrt 3 \ over \ sqrt 2} = U_d \ cdot \ sqrt 3$$

Udf- wirkende Interphase , es ist auch eine lineare Spannung.

Vorausgesetzt, die Amplitude jeder Phase $$$U_f \ ca. 311B$ wir verstehen das $$$U_ {df} \ ca. 380B$ für Zwischenphasenspannung. Die Figur zeigt deutlich, wie eine Grenzflächenspannung gebildet wird, die aus zwei Phasenspannungen der Phasen F1 und F2 als F1- F2 bezeichnet wird . Die Spannung der Phasen F1 und F2 wird relativ zum Neutralleiter gemessen. Die Netzspannung F1-F2 wird zwischen zwei verschiedenen Phasenleitern gemessen.



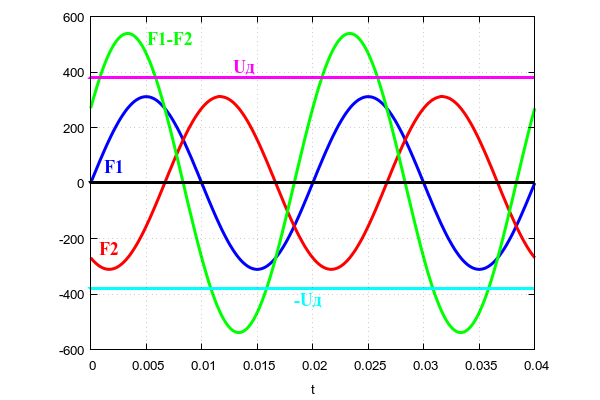
Wie Sie sehen können, ist die aktuelle Zwischenphasenspannung größer als die Amplitude der sinusförmigen Spannung einer Phase.

Die Amplitude der Grenzflächenspannung beträgt:

$$

$$U_ {mf} = U_ {df} \ cdot \ sqrt 2 = 380B \ cdot \ sqrt 2 \ ca. 538B$$

Im schlimmsten Fall (Netzwerk 240 V und Phase-zu-Phase-Spannung 415 V und sogar 10% darüber) beträgt die Amplitude der Phase-zu-Phase-Spannung:

$$

$$U_ {mf} = U_ {df} \ cdot \ sqrt 2 = (415B + 10 \%) \ cdot \ sqrt 2 \ ca. 645B$$

Denken Sie daran, wenn Sie in dreiphasigen Netzwerken arbeiten, und wählen Sie Elemente mit einer Nennspannung von mindestens 650 V, wenn sie zwischen zwei Phasen arbeiten müssen!

Ich hoffe jetzt ist klar, was das Wechselspannungsmessgerät anzeigt.

Fazit

Ganz kurz, fast an den Fingern, haben wir uns mit den Spannungen in Haushaltsnetzwerken vertraut gemacht. Um die Zusammenfassung aller oben genannten zusammenzufassen.

• Die Phasenspannung ist die Spannung zwischen der Phase und dem Neutralleiter.
• Die lineare oder Zwischenphasenspannung ist die Spannung zwischen zwei verschiedenen Phasendrähten desselben Dreiphasennetzwerks.
• In HF-Wechselstromnetzen gibt es drei, wenn auch enge, aber unterschiedliche Standards (Phase / Linear): 220 V / 380 V, 230 V / 400 V und 240 V / 415 V Wechselstrom mit einer Frequenz von 50 Hz.
• Ein Wechselstromvoltmeter zeigt normalerweise die effektive Spannung an (die auch effektiv ist, es ist auch effektiv ), die $$$\ sqrt 2$ mal kleiner als die Spitzenspannung (Amplitudenspannung) im Netzwerk.
• Im schlimmsten Fall beträgt die Spitzenphasenspannung aus Sicht der Normen ungefähr 373 V und die Spitzenleitungsspannung 645 V. Dies sollte bei der Entwicklung elektronischer Schaltungen berücksichtigt werden.

Ich hoffe, dieser Artikel hat jemandem geholfen, das Thema zu klären und einige Fragen für sich selbst zu beantworten.

Sie können Vorschläge und Wünsche, Tippfehler und nur Meinungen in einem Kommentar oder per E-Mail senden : shiotiny@yandex.ru .