Quasi-Newtonsche Methoden oder wenn es zu viele zweite Ableitungen für Athos gibt

Bei der ersten Bekanntschaft mit quasi-Newtonschen Methoden kann man zweimal überrascht sein. Erstens ergeben sich nach einem kurzen Blick auf die Formeln Zweifel, dass dies überhaupt funktionieren kann. Sie funktionieren jedoch. Weiterhin scheint es zweifelhaft, dass sie gut funktionieren werden. Und es ist umso überraschender zu sehen, wie viel schneller sie sind als die verschiedenen Variationen des Gefälles, nicht bei speziell konstruierten Aufgaben, sondern bei realen Aufgaben aus der Praxis. Und wenn danach immer noch Zweifel mit Interesse vermischt sind, müssen Sie verstehen, warum dieses Etwas überhaupt funktioniert.

Der Ursprung und die Grundideen, die Gradientenmethoden antreiben, einschließlich der Newton-Methode, wurden bereits berücksichtigt . Wir haben uns nämlich auf die Informationen über das Verhalten der Funktion in der Nähe der aktuellen Position gestützt, was uns eine einfache mathematische Analyse ermöglicht. Es wurde zumindest davon ausgegangen, dass uns Informationen zu den ersten Derivaten zur Verfügung standen. Was ist, wenn dies alles ist, was uns zur Verfügung steht? Ist Gradientenabstieg unser Satz? Natürlich, ja, es sei denn, Sie erinnern sich plötzlich daran, dass es sich um einen Prozess handelt, bei dem die Zielfunktion ordnungsgemäß verarbeitet wird. Und wenn ja, warum verwenden wir die gesammelten Informationen über das Verhalten der Funktion nicht, um unseren Gang auf ihrer Oberfläche etwas weniger blind zu machen?

Die Idee, Informationen über den zurückgelegten Weg zu verwenden, steht im Mittelpunkt der meisten Möglichkeiten, die Abstiegsmethoden zu beschleunigen. Dieser Artikel beschreibt eine der effektivsten, wenn auch nicht die billigste Art, diese Art von Informationen zu berücksichtigen, was zur Idee quasi-Newtonscher Methoden führt.

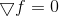
Um zu verstehen, wo die Beine der quasi-Newtonschen Methoden wachsen und woher der Name kommt, müssen wir wieder zur Minimierungsmethode zurückkehren, die auf der direkten Lösung der stationären Punktgleichung basiert . So wie die Betrachtung der Newton-Methode, die auf die Lösung dieser Gleichung angewendet wurde, uns zu der gleichnamigen Optimierungsmethode führte (die im Gegensatz zu ihrem Vorläufer eine globale Konvergenzregion aufweist), können wir erwarten, dass die Berücksichtigung anderer Methoden zur Lösung von Systemen nichtlinearer Gleichungen fruchtbar sein wird Planen Sie Ideen für den Aufbau anderer Optimierungsmethoden.

Sekantenmethoden

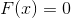
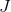
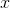
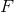
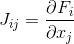
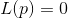
Ich möchte Sie daran erinnern, dass die Newton-Methode zur Lösung des Gleichungssystems , basiert auf dem Austausch in der Nähe eines Punktes in der Nähe der Lösung die Funktionen seine lineare Annäherung wo Ist ein linearer Operator, der, wenn ist ein Vektor und hat partielle Ableitungen in Bezug auf jede Variable, fällt mit der Jacobi-Matrix zusammen . 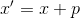Als nächstes wird die Gleichung gelöst und Punkt als neue Annäherung an die gewünschte Lösung genommen. Es ist einfach und es funktioniert.

Aber was ist, wenn wir aus irgendeinem Grund die Jacobi-Matrix nicht berechnen können? Das erste, was uns in diesem Fall einfällt, ist, dass wir, wenn wir die partiellen Ableitungen nicht analytisch berechnen können, eine numerische Näherung für sie erhalten können. 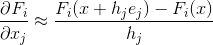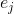Die einfachste (wenn auch keineswegs einzige) Option für eine solche Annäherung kann die Formel der richtigen endlichen Differenzen sein: wo Ist der j-te Basisvektor. Die aus solchen Näherungen zusammengesetzte Matrix wird mit bezeichnet . 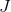Eine Analyse, wie viel Ersatz auf In Newtons Methode wirkt sich die Konvergenz auf eine ziemlich große Anzahl von Werken aus, aber in diesem Fall interessieren wir uns für einen anderen Aspekt. 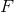Eine solche Annäherung erfordert nämlich die Berechnung der Funktion an N zusätzlichen Punkten und zusätzlich der Funktion an diesen Punkten interpoliert die Funktion d.h.



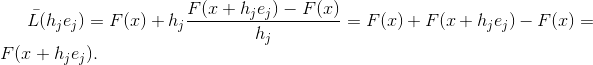
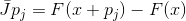
Nicht jede Approximation der Jacobi-Matrix hat diese Eigenschaft, aber jede Matrix einer affinen Funktion, die diese Eigenschaft hat, ist eine Approximation der Jacobi-Matrix. In der Tat, wenn und dann bei . Diese Eigenschaft, nämlich die Interpolationseigenschaft, gibt uns eine konstruktive Möglichkeit, die Newton-Methode zu verallgemeinern.

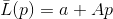
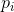
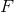
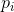
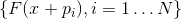
Lass - Funktion, die die Anforderung erfüllt für ein System linear unabhängiger Vektoren . Dann wird eine solche Funktion als Sekantenfunktion bezeichnet und die Gleichung, die es definiert, ist die Sekantengleichung . 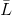Wenn das System der Vektoren ist vollständig (das heißt, es gibt genau N von ihnen und sie sind immer noch linear unabhängig), und zusätzlich das Vektorsystem dann linear unabhängig eindeutig definiert.

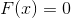
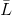
Jede Methode, die auf einer lokalen Änderung der Gleichung basiert Gleichung der Form wo erfüllt die Sekantengleichung , die als Sekantenmethode bezeichnet wird .

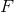
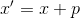
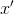
Es stellt sich die Frage, wie der Sekant für eine Funktion auf rationellste Weise konstruiert werden kann. . Die folgende Argumentation scheint offensichtlich: Lassen Sie am Punkt x ein affines Modell konstruieren, das die gegebene Funktion an den Punkten interpoliert . Gleichungslösung gibt uns einen neuen Punkt . 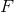Dann, um an einem Punkt ein affines Modell zu erstellen Es ist am sinnvollsten, Interpolationspunkte so zu wählen, dass der Wert bereits bekannt - das heißt, nehmen Sie sie aus dem Set . 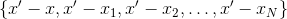Es gibt verschiedene Optionen, für die Sie aus den vielen zuvor verwendeten Punkten auswählen können. 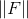Sie können beispielsweise diejenigen als Interpolationspunkte verwenden, in denen zählt am wenigsten oder nur am ersten Punkte. Auf jeden Fall scheint es offensichtlich, dass sollte in vielen Interpolationspunkten für das neue affine Modell enthalten sein. 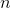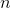Also darüber hinaus Schritte des iterativen Prozesses in unserem Set können bis zu sein Verschiebungen, die auf zuvor übergebenen Punkten aufgebaut sind. 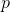Wenn der Prozess so aufgebaut ist, dass das neue affine Modell nicht mehr verwendet Von den vorherigen Werten wird ein solcher Prozess als p-Punkt-Sekantenmethode bezeichnet.

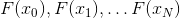
Auf den ersten Blick scheint die N-Punkt-Sekantenmethode der beste Kandidat für die Rolle des Ersetzens der Newton-Methode zu sein, da sie die Informationen, die wir beim Lösen erhalten, maximal nutzt und gleichzeitig die Anzahl zusätzlicher Berechnungen minimiert - wir verwenden den Wert der Funktion in letzterer N Punkte bestanden. Dies ist leider nicht so. Die Sache ist, dass das Vektorsystem weigert sich hartnäckig, linear unabhängig mit einem ausreichend großen N zu sein. Selbst wenn sich herausstellt, dass diese Bedingung erfüllt ist und das entsprechende affine Modell noch existiert, besteht die Möglichkeit, dass die Richtungen erweisen sich auch als linear unabhängig, es stellt sich noch weniger heraus. Und dies beinhaltet die Tatsache, dass das affine Modell, obwohl es existiert, entartet und praktisch ungeeignet ist.

Im Allgemeinen ist die 2-Punkt-Sekantenmethode am stabilsten. Das heißt, eine Methode, bei der bei jeder Iteration zusätzliche N-1-Werte der Funktion berechnet werden müssen. Dies ist eindeutig nicht für unsere praktischen Zwecke geeignet.

Dann ist die Frage - was war das alles?

Quasi-Newtonsche Methoden zur Lösung von Gleichungen

Der Ausweg ist einfach, wenn auch nicht offensichtlich. Wenn wir nicht die technische Fähigkeit haben, basierend auf den bereits berechneten Werten das affine Modell, das die Sekantengleichung erfüllt, eindeutig zu bestimmen, ist dies nicht erforderlich. Wir nehmen die Sekantengleichung als Grundlage, aber wir werden verlangen, dass sie nur für ein unvollständiges Vektorsystem erfüllt ist . Mit anderen Worten, wir werden verlangen, dass die Interpolationsbedingung nur für eine ausreichend kleine Anzahl bekannter Werte erfüllt ist. In diesem Fall können wir natürlich nicht mehr garantieren, dass die in einem solchen Modell verwendete Matrix zur Jacobi-Matrix tendiert, aber wir werden dies nicht benötigen. Hinzu kommt, dass das affine Modell die Funktion am aktuellen Punkt interpolieren muss, d. H. erhalten wir die folgende Formulierung der Sekantenmethode:



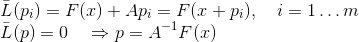
Bruiden war der erste, der Methoden dieser Art für m = 1 in Betracht zog und sie quasi-Newtonsch nannte. Es ist klar, dass die Sekantenbedingung in diesem Fall es uns ermöglicht, die Matrix eindeutig zu identifizieren nur wenn ihm zusätzliche Bedingungen auferlegt werden und jede dieser zusätzlichen Bedingungen zu einer eigenen Methode führt. Bruyden selbst argumentierte wie folgt:

als die Bewegung in die Richtung 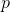von Punkt 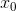auf den Punkt gibt uns keine zusätzlichen Informationen darüber, wie sich die Funktion in anderen als ändert 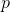Richtungen, dann die Wirkung der neuen affinen Funktion auf den Vektor sollte sich von der Wirkung der alten Funktion auf denselben Vektor unterscheiden, je weniger desto unterschiedlicher von 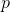. Als letztes Mittel, wenn orthogonal 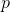sollte sich das Verhalten der neuen Funktion nicht vom Verhalten der alten unterscheiden.

Breidens Idee ist in ihrer Einfachheit brillant. Wenn wir keine neuen Informationen über das Verhalten der Funktion haben, können wir am besten versuchen, die alte nicht zu beschmutzen. Dann die zusätzliche Bedingung

für alle so dass

Mit dieser Option können Sie die Matrix der neuen Transformation eindeutig bestimmen. Sie wird durch Hinzufügen einer Rang 1-Korrektur zur alten Matrix erhalten.



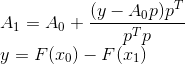
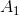
Trotz der Einfachheit und Konsistenz der Schlussfolgerungen von Bruiden bieten sie jedoch nicht den Dreh- und Angelpunkt, der als Grundlage für die Konstruktion anderer ähnlicher Methoden dienen könnte. Glücklicherweise gibt es einen formelleren Ausdruck seiner Idee. Die Matrix ist nämlich auf diese Weise aufgebaut Es stellt sich als Lösung für das folgende Problem heraus:



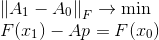
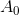
Die Aufgabenbeschränkung ist nichts anderes als die Sekantengleichung, und die Minimierungsbedingung spiegelt unseren Wunsch wider, so viele Informationen wie möglich in der Matrix zu speichern . Das Maß für die Diskrepanz zwischen den Matrizen ist in diesem Fall die Frobenius-Norm, in der das gestellte Problem eine eindeutige Lösung hat. Diese Formulierung kann durchaus als Ausgangspunkt für die Konstruktion anderer Methoden dienen. Wir können nämlich sowohl das Maß ändern , mit dem wir die eingeführten Änderungen bewerten, als auch die der Matrix auferlegten Bedingungen verschärfen. Im Allgemeinen kann man bereits mit einer solchen Formulierung der Methode arbeiten.

Quasi-Newton-Optimierungsmethoden

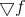
Nachdem wir die Hauptidee verstanden haben, können wir endlich zu Optimierungsproblemen zurückkehren und feststellen, dass die Anwendung der Bruyden-Formel zur Neuberechnung des affinen Modells nicht sehr gut zu unserer Aufgabe passt. Tatsächlich ist die erste Ableitung der Gradientenfunktion es gibt nichts anderes als die hessische Matrix, die konstruktionsbedingt symmetrisch ist. 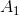Gleichzeitig führt die Aktualisierung nach der Bruyden-Regel zu einer asymmetrischen Matrix auch wenn war symmetrisch. Dies bedeutet nicht, dass die Bruden-Methode nicht zur Lösung der stationären Punktgleichung angewendet werden kann, aber basierend auf einer solchen Aktualisierungsregel ist es unwahrscheinlich, dass wir gute Optimierungsmethoden konstruieren können. Im Allgemeinen ist es ziemlich offensichtlich, dass die Quasi-Newton-Methode umso besser funktionieren sollte, je genauer das System der Bedingungen des Problems die Besonderheiten einer bestimmten Jacobi-Matrix beschreibt.

Um diesen Nachteil zu beheben, fügen wir dem Broyden-Minimierungsproblem eine zusätzliche Einschränkung hinzu, die ausdrücklich erfordert, dass die neue Matrix zusammen mit der alten symmetrisch ist:



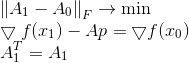
Die Lösung für dieses Problem ist



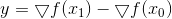
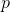
Hier und die Matrix-Neuberechnungsformel ist nach ihren Erstellern benannt - Powell, Shanno und Bruyden (PSB). Die resultierende Matrix ist symmetrisch, aber eindeutig nicht eindeutig positiv, wenn auch nur plötzlich wird nicht kollinear sein . Und wir haben gesehen, dass positive Sicherheit bei Optimierungsmethoden sehr wünschenswert ist.

Wieder werden wir den Zustand des Problems korrigieren, indem wir diesmal die skalierte Frobenius-Norm als Maß für die Matrixdivergenz verwenden.



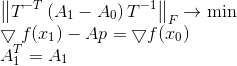
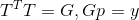
Der Ursprung einer solchen Aussage der Frage ist ein separates großes Thema, aber es ist interessant, dass, wenn die Matrix T so ist, dass (das heißt, G ist auch eine affine Transformationsmatrix, die die Sekantengleichung für die Richtung p erfüllt), dann stellt sich heraus, dass die Lösung dieses Problems unabhängig von der Wahl von T ist und zur Aktualisierungsformel führt



bekannt als die Davidon-Fletcher-Powell-Formel. Diese Aktualisierungsmethode hat sich in der Praxis bewährt, da sie die folgende Eigenschaft aufweist:

wenn und 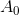positiv definitiv dann 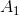auch positiv identifiziert.

Ich stelle danach fest, dass, wenn die erste Bedingung nicht erfüllt ist, keine affine Funktion mit einer positiven bestimmten Matrix existiert, die die Sekantengleichung erfüllt.

Wenn wir in dem Problem, das zur DFP-Methode führt, als Maß für die Diskrepanz affiner Modelle den Abstand nicht zwischen den Matrizen selbst, sondern zwischen den zu ihnen inversen Matrizen nehmen, erhalten wir ein Problem



Seine Lösung ist eine bekannte Formel, die fast gleichzeitig von Breiden, Fletcher, Goldfarb und Shanno (BFGS) entdeckt wurde.



Bisher wird angenommen, dass eine Neuberechnung nach dieser Formel aus rechnerischer Sicht am effizientesten ist und gleichzeitig weniger anfällig für eine Degeneration der Matrix mit einer großen Anzahl von Iterationen ist. Unter den gleichen Bedingungen wie DFP bewahrt diese Formel die Eigenschaft der positiven Bestimmtheit.

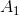
Alle beschriebenen Methoden zum Aktualisieren der Matrix erfordern eine Korrektur von Rang 2. Dies macht es einfach und leicht, die Matrix zu invertieren unter Verwendung der Sherman-Morrison-Formel und des Wertes .



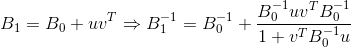
vorausgesetzt, der Nenner der Formel ist ungleich Null. Ich werde keine spezifischen Formeln zum Aktualisieren der inversen Matrizen der aufgelisteten Methoden angeben, da sie leicht zu finden oder unabhängig voneinander abzuleiten sind. Das einzige, was in diesem Fall beachtet werden sollte, ist, dass Varianten von Methoden mit Aktualisierung der inversen Matrix normalerweise viel weniger stabil sind (das heißt, sie leiden mehr unter Rundungsfehlern) als diejenigen, die eine Aktualisierung der ursprünglichen Matrix vorschlagen. Es ist am effektivsten, nicht die Matrix selbst, sondern ihre Cholesky-Zerlegung zu aktualisieren (es sei denn natürlich, eine solche Zerlegung findet statt), da eine solche Implementierungsoption numerisch stabiler ist und außerdem die Kosten für die Lösung einer Gleichung minimiert, die die Bewegungsrichtung bestimmt.

Es bleibt die Frage zu prüfen, wie die allererste Matrix im quasi-Newtonschen Prozess aussehen soll. Hier ist alles offensichtlich - je näher es der hessischen Matrix oder ihrer korrigierten Version ist, wenn sich das hessische plötzlich nicht als positiv definitiv herausstellt, desto besser wird es unter dem Gesichtspunkt der Konvergenz sein. Grundsätzlich kann jedoch jede positive definitive Matrix für uns geeignet sein. Die einfachste Version einer solchen Matrix ist eine einzelne, und dann fällt die erste Iteration mit der Iteration des Gradientenabfalls zusammen. Fletcher und Powell zeigten (natürlich für die DFP-Methode), dass wenn die quadratische Funktion minimiert wird, unabhängig davon, welche (positiv definierte) Matrix als anfängliche DFP-Iteration verwendet wird, sie zu einer Lösung in genau N Iterationen führen, wobei N ist Dimension des Problems, und die quasi-Newtonsche Matrix fällt mit der hessischen Matrix am minimalen Punkt zusammen. Im allgemeinen nichtlinearen Fall eines solchen Glücks werden wir natürlich nicht warten, aber dies gibt zumindest Anlass, sich nicht zu viele Sorgen über die schlechte Wahl der Ausgangsmatrix zu machen.

Fazit

Der beschriebene Ansatz zur Konstruktion quasi-Newtonscher Methoden ist nicht der einzig mögliche. Zumindest kamen die Entdecker der beschriebenen quasi-Newtonschen Methoden und viele nachfolgende Forscher aufgrund völlig unterschiedlicher Überlegungen zu denselben Formeln. Es ist jedoch interessant, dass, sobald eine bestimmte quasi-Newtonsche Methode auftauchte, nach relativ kurzer Zeit klar wurde, dass es sich um eine Lösung für ein sehr leicht zu interpretierendes Optimierungsproblem handelt. Meiner Meinung nach ist es bemerkenswert, dass es möglich ist, einen gemeinsamen Nenner für so unterschiedliche Methoden zu liefern, da dies die Grundlage für die Konstruktion anderer Methoden bildet, die die Besonderheiten einer bestimmten Aufgabe besser berücksichtigen. Insbesondere gibt es quasi-Newtonsche Methoden zur Aktualisierung spärlicher Matrizen, Methoden, bei denen so wenig Elemente wie möglich geändert werden, und viele andere wären eine Fantasie.

Es sollte auch beachtet werden, dass die Methoden variabler Metriken trotz ihres Namens nicht immer zur Konstruktion von Matrizen führen, die tatsächlich Metriken sind, obwohl sie dies jedes Mal tun, wenn es überhaupt möglich ist.Dies ist normalerweise kein großes Problem, aber diejenigen, die sich vor einer möglichen Verlegenheit schützen möchten, greifen möglicherweise auf dieselben Tricks zurück, die zur Überwindung eines ähnlichen Problems mit der Newton-Methode angewendet wurden - beispielsweise durch Richtungsänderung oder Anwendung des Levenberg-Marquardt-Schemas . In diesem Fall werden zwar Fragen der Wahl der Form einer vertrauensvollen Region wieder relevant, aber hier ist es notwendig, das kleinere Übel zu wählen. Eine andere Lösung des Problems besteht darin, lineare Suchmethoden zu verwenden, um sicherzustellen, dass die notwendigen Bedingungen zur Aufrechterhaltung einer positiven Sicherheit erfüllt sind. Die Wolfe-Regel garantiert die Erfüllung dieser Bedingung, während die Armijo- und Goldstein-Regeln dies nicht tun.

Theoretisch ist es fast unmöglich zu bestimmen, welche der vielen möglichen quasi-Newtonschen Methoden in Bezug auf eine bestimmte Klasse von Problemen am effektivsten ist. Normalerweise beschränken sie sich bei der Formulierung einer Methode darauf, ihre Wirksamkeit bei der Minimierung einer quadratischen Funktion zu zeigen (eine Methode wird übrigens als effektiv angesehen, wenn sie zu einer exakten Lösung in N Iterationen führt, dh nicht langsamer als direkte Methoden zur Lösung von SLAEs). In selteneren Fällen kann man Studien zur Konvergenzreihenfolge der Methode (die normalerweise superlinear ist, dh deutlich besser als die Gradientenabnahme), zur Stabilität und zu anderen interessanten Merkmalen finden. Im Allgemeinen ist das einzig vernünftige Kriterium für die Beurteilung der Wirksamkeit einer bestimmten Methode für eine bestimmte Aufgabenklasse die Praxis.Also Schaufeln in der Hand - und Erfolg bei der Anwendung.