Im JeMalloc. Kerndatenstrukturen: Pairing von Heap- und Bitmap-Baum

Das Thema Allocators taucht häufig im Internet auf: In der Tat ist ein Allocator eine Art Eckpfeiler, das Herz jeder Anwendung. In dieser Reihe von Beiträgen möchte ich ausführlich auf einen sehr unterhaltsamen und herausragenden Allokator eingehen - JeMalloc , der von Facebook unterstützt und entwickelt und beispielsweise in bionic [Android] lib C verwendet wird.

Im Netzwerk konnte ich keine Details finden, die die Seele dieses Allokators vollständig enthüllen, was letztendlich die Unmöglichkeit beeinträchtigte, Schlussfolgerungen über die Anwendbarkeit von JeMalloc bei der Lösung eines bestimmten Problems zu ziehen. Es kam viel Material heraus und um zu lesen, dass es nicht anstrengend war, schlage ich vor, mit den Grundlagen zu beginnen: Grundlegende Datenstrukturen, die in JeMalloc verwendet werden.

Unter der Katze spreche ich von Pairing Heap und Bitmap Tree , die die Grundlage von JeMalloc bilden. An dieser Stelle gehe ich nicht auf das Thema Multithreading und Feinkörniges Sperren ein. Wenn ich jedoch die Reihe der Beiträge fortsetze, werde ich Ihnen auf jeden Fall etwas über diese Dinge erzählen, für die tatsächlich verschiedene Arten von Exoten geschaffen werden, insbesondere die unten beschriebene.

Bitmap_s ist eine baumartige Datenstruktur, mit der Sie:

• Finden Sie schnell das erste gesetzte / nicht gesetzte Bit in einer bestimmten Bitfolge.
• Ändern Sie und erhalten Sie den Wert eines Bits mit dem Index i in einer bestimmten Folge von Bits.
• Der Baum wird gemäß einer Folge von n Bits erstellt und hat die folgenden Eigenschaften:
• Die Basiseinheit des Baums ist der Knoten, und die Basiseinheit des Knotens ist das Bit. Jeder Knoten besteht aus genau k Bits. Die Bitigkeit eines Knotens wird so ausgewählt, dass die logischen Operationen in einem ausgewählten Bitbereich auf einem bestimmten Computer so schnell und effizient wie möglich berechnet werden. In JeMalloc wird ein Knoten durch einen vorzeichenlosen langen Typ dargestellt.
• Die Höhe des Baumes wird in Ebenen gemessen und für eine Folge von n Bits ist H = $$$\ log_ {k} {n} log k (n)$Ebenen.
• Jede Ebene des Baums wird durch eine Folge von dargestellt $$$countOfNodesOnLevel = integerCeil (\ frac {n} {{k} ^ {H - currentLevel + 1}})$Knoten, was einer Folge von entspricht $$$countOfBitsOnLevel = countOfNodesOnLevel * k$bisschen.
• Die höchste (Wurzel-) Ebene des Baums besteht aus k Bits und die niedrigste aus n Bits.
• Jedes Bit eines Knotens der Ebene L bestimmt den Zustand aller Bits eines untergeordneten Knotens der Ebene L - 1: Wenn ein Bit auf Besetzt gesetzt ist, werden auch alle Bits eines untergeordneten Knotens auf Besetzt gesetzt, andernfalls können Bits eines untergeordneten Knotens vorhanden sein "beschäftigt" und "frei" Zustand.

Es ist sinnvoll, bitmap_t in zwei Arrays darzustellen: das erste einer Dimension, die der Anzahl aller Baumknoten entspricht - um die Baumknoten zu speichern, und das zweite der Baumhöhendimension - um den Versatz des Anfangs jeder Ebene im Array der Baumknoten zu speichern. Bei dieser Methode zum Angeben eines Baums kann das Stammelement zuerst und dann nacheinander die Knoten der einzelnen Ebenen verwenden. JeMalloc-Autoren speichern jedoch das Stammelement als letztes im Array, und davor befinden sich die Knoten der zugrunde liegenden Baumebenen.

Nehmen Sie als anschauliches Beispiel eine Folge von 92 Bits und K = 32 mind. Wir nehmen an, dass der Zustand "frei" ist - bezeichnet durch ein einzelnes Bit, und der Zustand "beschäftigt" - Null. Es sei auch angenommen, dass in der ursprünglichen Bitsequenz das Bit mit dem Index 1 (in der Abbildung von Null nach rechts von links) in den Besetztzustand versetzt wird. Dann sieht bitmap_t für eine solche Bitsequenz wie im Bild unten aus:



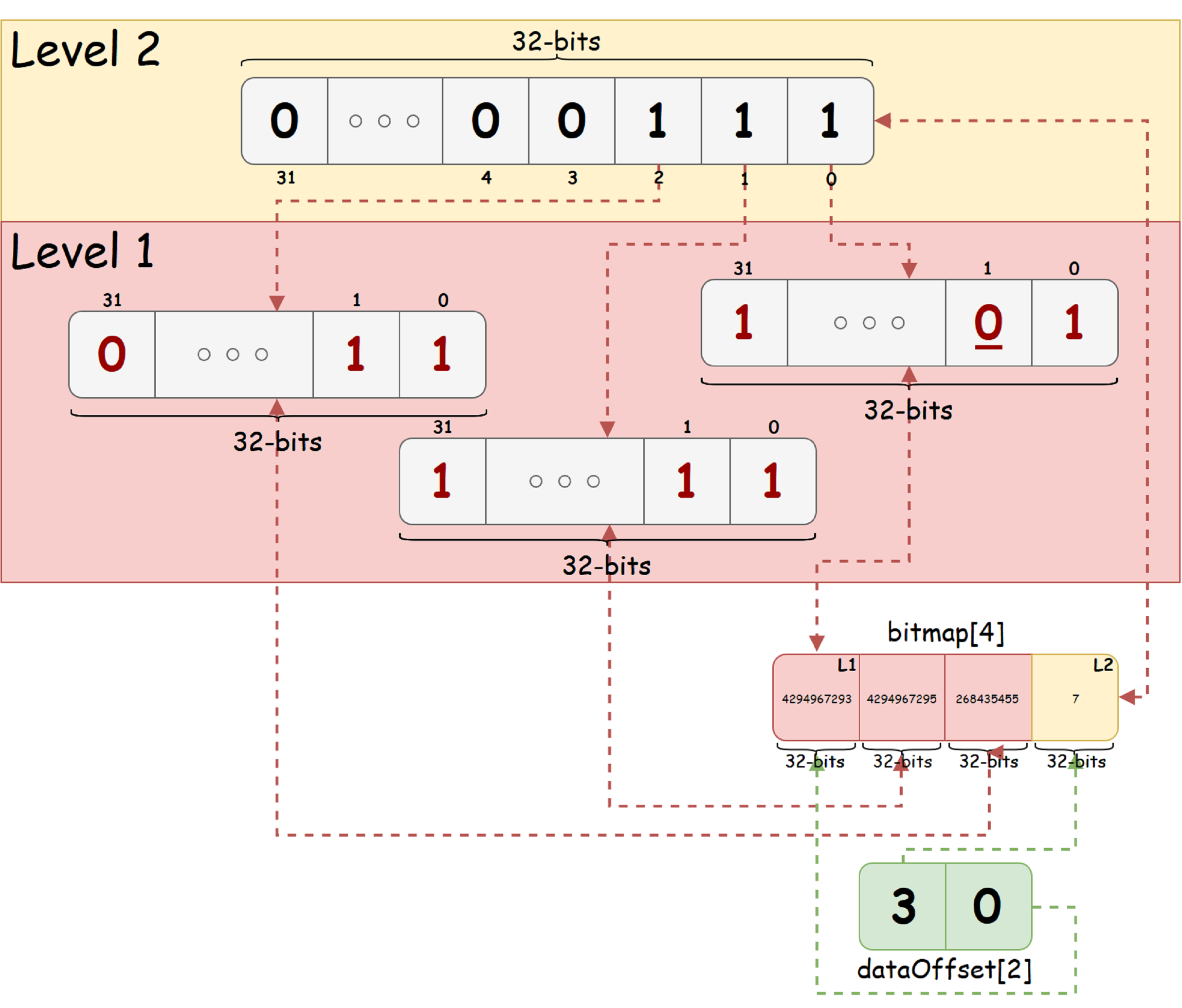Aus der Abbildung sehen wir, dass der resultierende Baum nur zwei Ebenen hat. Die Wurzelebene enthält 3 Einheitsbits, die das Vorhandensein von sowohl freien als auch belegten Bits in jedem der untergeordneten Knoten des entsprechenden Bits anzeigen. In der unteren rechten Ecke sehen Sie die Baumansicht in zwei Arrays: alle Baumknoten und Offsets jeder Ebene im Knotenarray.

Unter der Annahme, dass bitmap_t durch zwei Arrays dargestellt wird (ein Datenarray und ein Array von Offsets auf Baumebene im Datenarray), beschreiben wir die Operation zum Finden des ersten niedrigstwertigen Bits in einem gegebenen Bitmap_t:

• Ausgehend vom Wurzelknoten führen wir die Suchoperation für das erste niedrigstwertige Bit des Knotens durch: Um dieses Problem zu lösen, stellen moderne Prozessoren spezielle Anweisungen bereit, die die Suchzeit erheblich verkürzen können. Wir werden das gefundene Ergebnis in der Variablen FirstSetedBit speichern .
• Bei jeder Iteration des Algorithmus behalten wir die Summe der Positionen der gefundenen Bits bei: countOfSettedBits + = FirstSetedBit
• Unter Verwendung des Ergebnisses des vorherigen Schritts gehen wir zum untergeordneten Knoten des ersten niedrigstwertigen Einheitsbits des Knotens und wiederholen den vorherigen Schritt. Der Übergang erfolgt nach folgender einfacher Formel: $$$currentNode = bitmapData [levelOffsetArray [currentLevel] + sumOfBits]$
• Der Prozess wird fortgesetzt, bis die niedrigste Ebene des Baums erreicht ist. countOfSettedBits - Die Nummer des gewünschten Bits in der Eingangsbitsequenz.

Pairing Heap ist eine Heap-ähnliche Baumdatenstruktur, mit der Sie:

• Fügen Sie je nach Implementierung ein Element mit einer konstanten zeitlichen Komplexität von O (1) und fortgeführten Anschaffungskosten von O (log N) oder O (1) ein .
• Suche mindestens nach konstanter Zeit - O (1)
• Führen Sie zwei Pairing Heap mit konstanter Zeitkomplexität zusammen - O (1) und fortgeführte Anschaffungskosten O (log N) oder O (1) - je nach Implementierung
• Löschen Sie ein beliebiges Element (insbesondere ein minimales) mit einer temporären Komplexitätsschätzung in O (N) und einer amortisierten Komplexitätsschätzung in O (log N).

Formal gesehen ist Pairing Heap ein beliebiger Baum mit einer dedizierten Wurzel, die die Eigenschaften des Heaps erfüllt (der Schlüssel jedes Scheitelpunkts ist nicht weniger / nicht mehr als der Schlüssel seines übergeordneten Scheitelpunkts).
Ein typischer Pairing Heap, bei dem der Wert des untergeordneten Knotens kleiner als der Wert des übergeordneten Knotens ist (auch bekannt als Min Pairing Heap), sieht ungefähr so ​​aus:



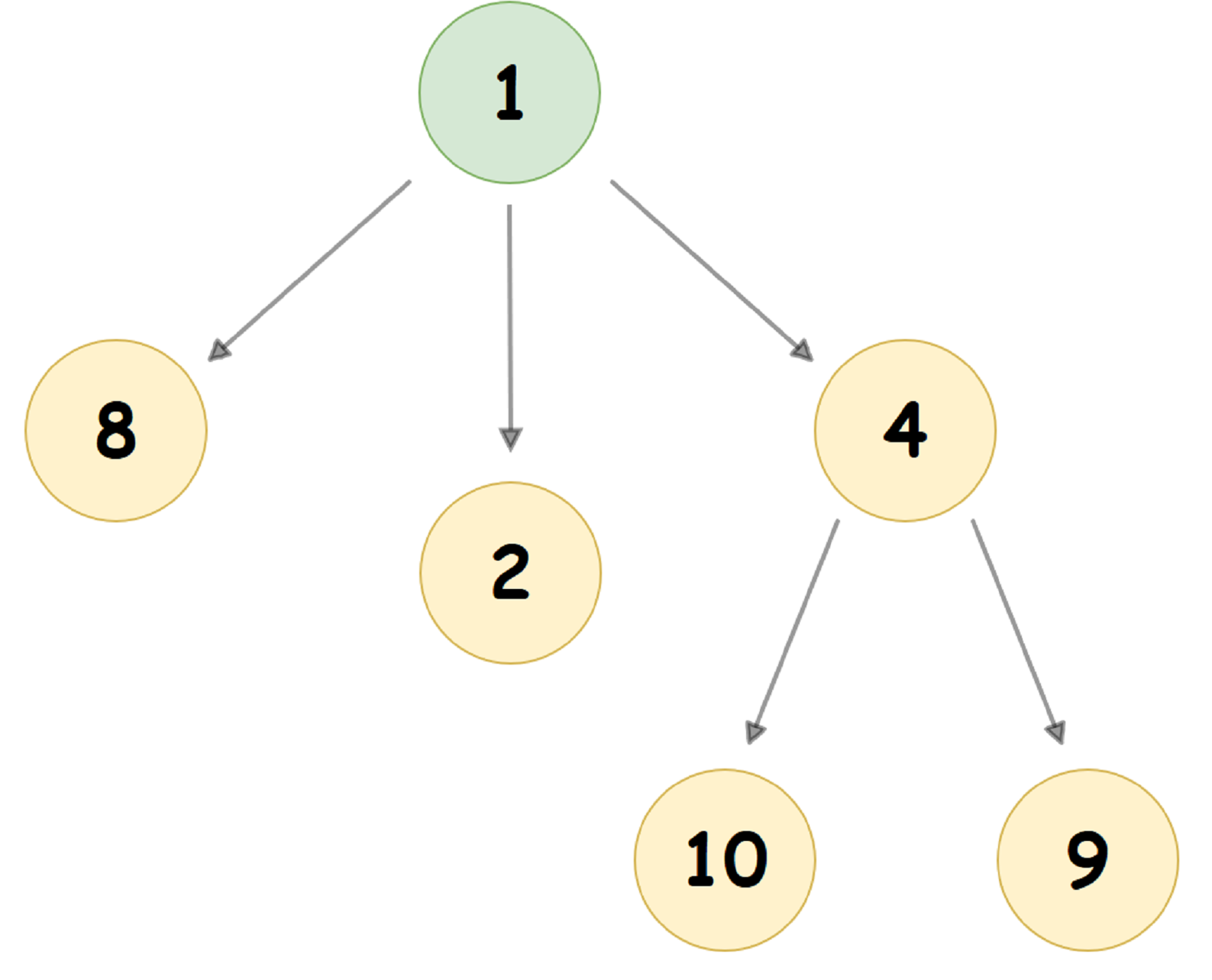
Im Arbeitsspeicher des Computers wird Pairing-Heap in der Regel ganz anders dargestellt: Jeder Knoten des Baums speichert 3 Zeiger:

• Zeiger auf den untersten Knoten ganz links des aktuellen Knotens
• Zeiger auf das linke Geschwister des Knotens
• Zeiger auf das rechte Geschwister des Knotens

Wenn einer der angegebenen Knoten fehlt, wird der entsprechende Knotenzeiger ungültig.
Für den in der obigen Abbildung dargestellten Heap erhalten wir die folgende Darstellung:



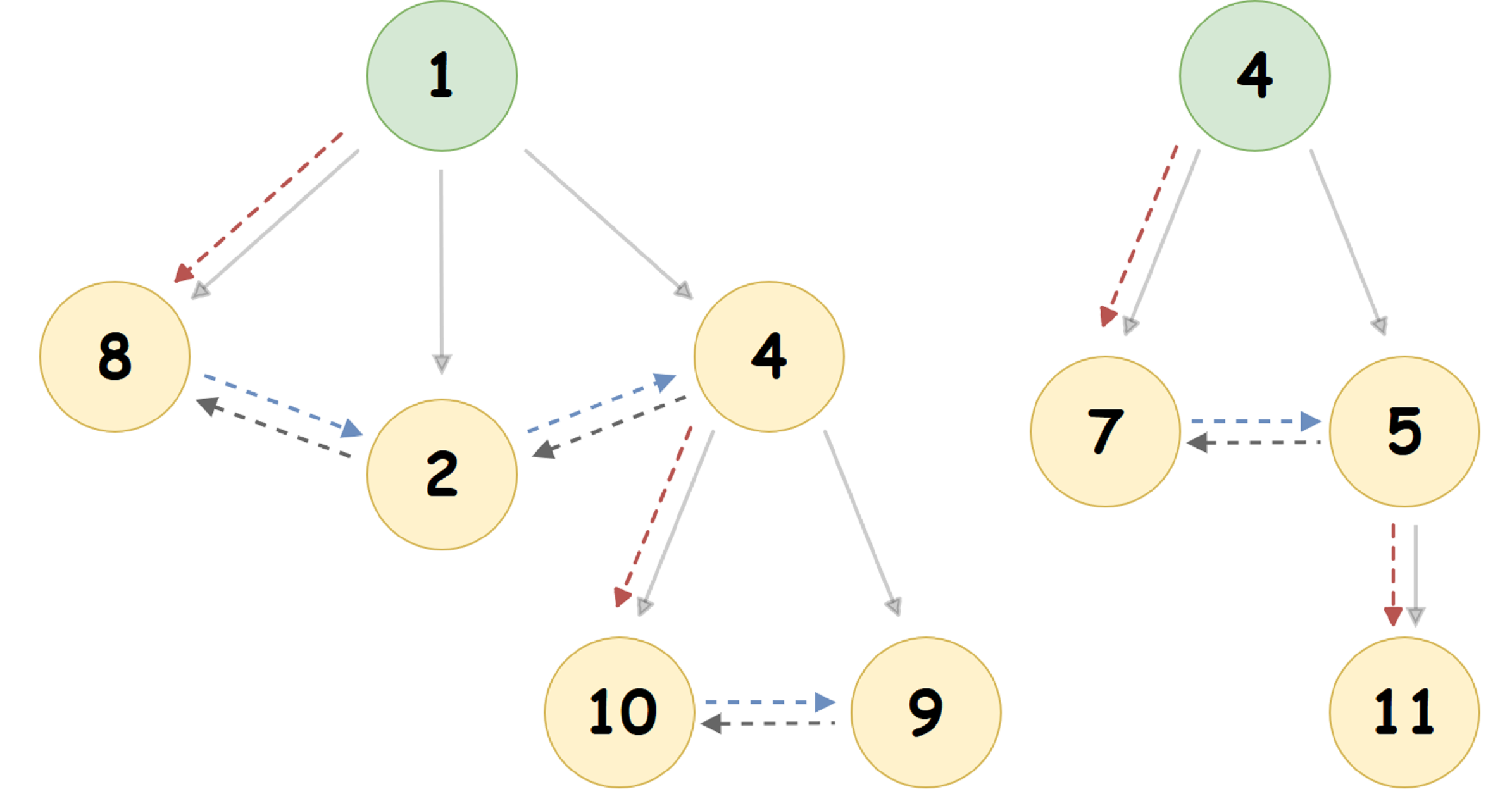Hier wird der Zeiger auf den untersten Knoten ganz links durch einen rot gepunkteten Pfeil angezeigt, der Zeiger auf den rechten Bruder des Knotens ist blau und der Zeiger auf den linken Bruder ist grau. Der durchgezogene Pfeil zeigt die Pairing Heap-Darstellung in einer baumartigen Form, die für eine Person üblich ist.

Bitte beachten Sie die folgenden zwei Fakten:

• An der Wurzel des Haufens gibt es immer keine rechten und linken Brüder.
• Wenn ein Knoten U einen Zeiger ungleich Null auf den untersten Knoten ganz links hat, ist dieser Knoten der 'Kopf' der doppelt verknüpften Liste aller untergeordneten Knoten von U. Diese Liste heißt siblingList.

Als nächstes listen wir den Algorithmus der Hauptoperationen im Min Pairing-Heap auf :

• Knoten in Pairing Heap einfügen:
  
  Es sei ein Pairing Heap mit einer Wurzel und einem Wert darin {R, V_1} sowie einem Knoten {U, V_2} gegeben . Wenn Sie dann einen U-Knoten in einen bestimmten Pairing Heap einfügen:
  
  • Wenn die Bedingung V_2 <V_1 erfüllt ist: U wird der neue Wurzelknoten des Heaps und verdrängt die Wurzel R an die Position ihres linken untergeordneten Knotens. Gleichzeitig wird der rechte Bruder des Knotens R sein ältester Knoten ganz links, und der Zeiger auf den Knoten ganz links des Knotens R wird Null.
  • Andernfalls: U wird zum untersten linken Knoten der Wurzel von R, und sein ältester Bruder wird zum äußersten linken Knoten der Wurzel von R.
• Zusammenführen von zwei Paarungshaufen:
  
  Es seien zwei Pairing Heaps mit Wurzeln und Werten {R_1, V_1} , {R_2, V_2} angegeben. Wir beschreiben einen der Algorithmen zum Zusammenführen solcher Heaps in den resultierenden Pairing Heap:
  
  • Wählen Sie den Heap mit dem niedrigsten Wert im Stammverzeichnis. Sei es ein Haufen {R_1, V_1}.
  • 'Trennen' Sie die Wurzel R_1 vom ausgewählten Heap: Dazu setzen wir einfach den Zeiger auf den untersten Knoten ganz links auf Null.
  • Machen Sie mit dem neuen Zeiger auf den untersten Knoten ganz links der Wurzel R_1 die Wurzel R_2. Beachten Sie, dass R_2 von nun an den Root-Status verliert und ein normaler Knoten im resultierenden Heap ist.
  • Wir setzen den rechten Bruder des Knotens R_2: Mit dem neuen Wert setzen wir den alten Zeiger (vor dem Nullstellen) auf den untersten Knoten ganz links der Wurzel R_1 und aktualisieren für R_1 den Zeiger auf den linken Bruder.

Betrachten Sie den Zusammenführungsalgorithmus anhand eines bestimmten Beispiels:



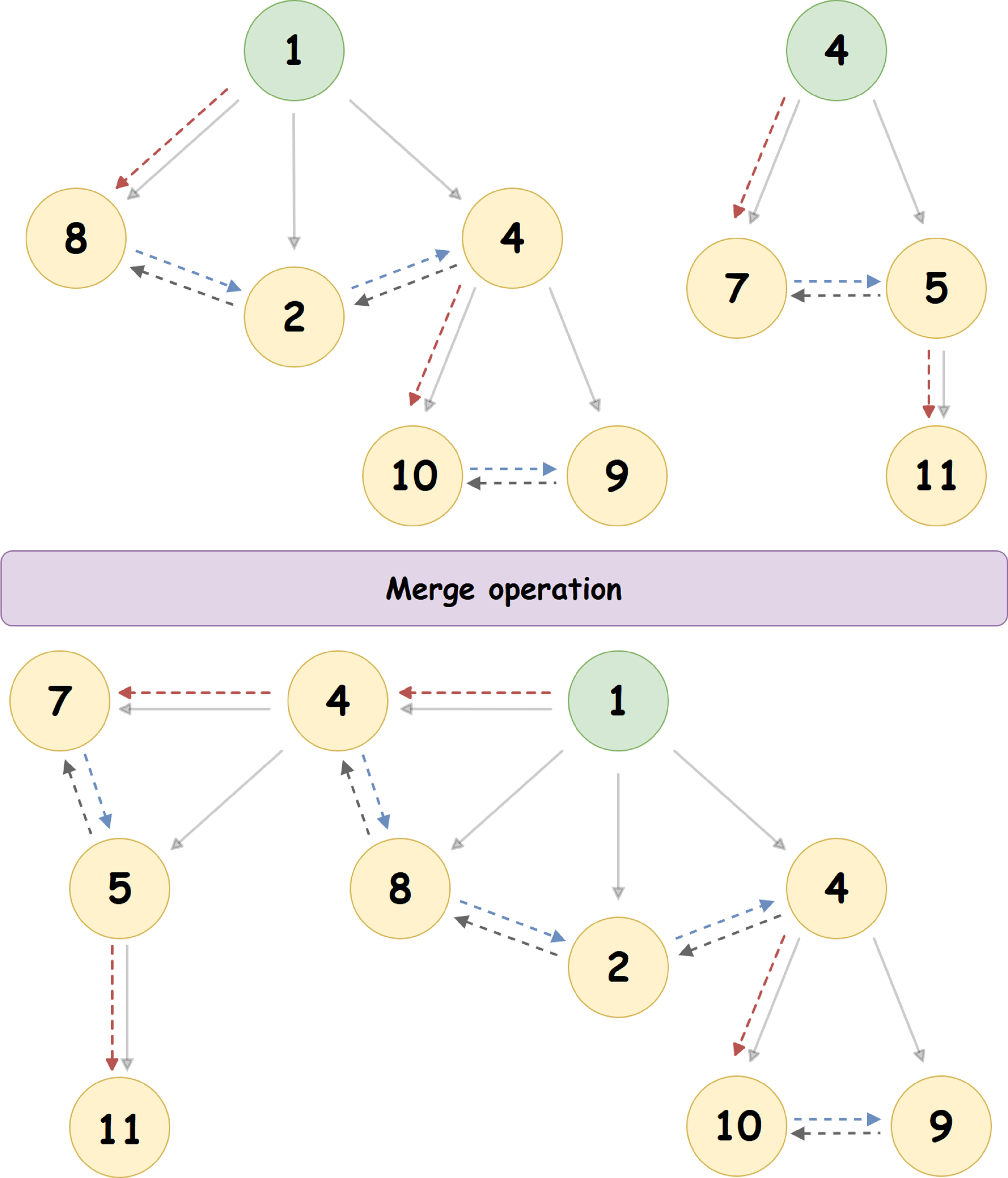Hier verbindet der Heap mit der Wurzel '4' den Heap mit der Wurzel '1' (1 <4) und wird zu seinem untersten Knoten ganz links. Der Zeiger auf den rechten Bruder des Knotens '4' - wird aktualisiert, ebenso der Zeiger auf den linken Bruder des Knotens '8'.

• Entfernen des Stamms (Knoten mit dem Mindestwert) Pairing Heap:
  
  Es gibt verschiedene Algorithmen zum Entfernen eines Knotens aus einem Pairing Heap, die garantiert eine amortisierte Schätzung der Komplexität in O (log N) liefern. Wir beschreiben einen von ihnen, den Multipass-Algorithmus, der in JeMalloc verwendet wird:
  
  
  • Wir löschen die Wurzel des angegebenen Heaps und lassen nur den untersten Knoten ganz links.
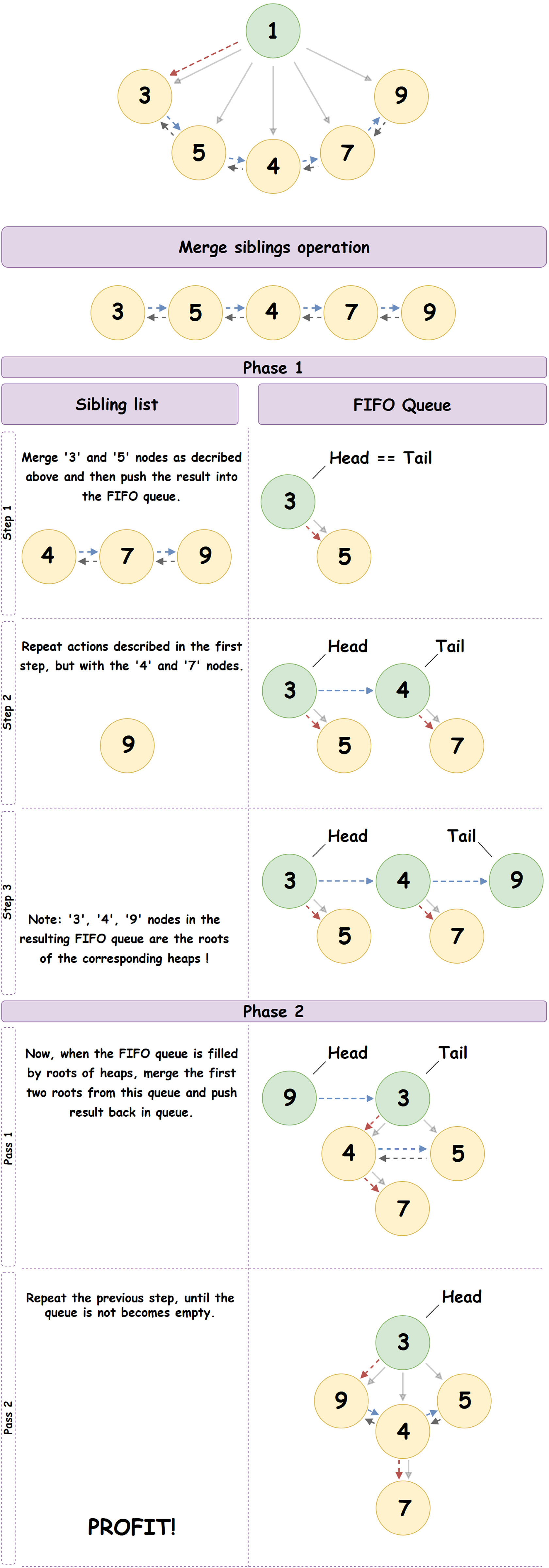
  • Der unterste Knoten ganz links bildet eine doppelt verknüpfte Liste aller untergeordneten Knoten des übergeordneten Knotens und in unserem Fall des zuvor gelöschten Stamms. Wir werden diese Liste nacheinander bis zum Ende durchgehen und unter Berücksichtigung der Knoten als Wurzeln des unabhängigen Pairing Heap den Vorgang des Zusammenführens des aktuellen Elements der Liste mit dem nächsten ausführen und das Ergebnis in eine vorbereitete FIFO-Warteschlange stellen.
  • Nachdem die FIFO-Warteschlange initialisiert wurde, werden wir sie durchlaufen und den Vorgang des Zusammenführens des aktuellen Elements der Warteschlange mit dem nächsten ausführen. Das Ergebnis der Fusion wird am Ende der Warteschlange platziert.
  • Wir wiederholen den vorherigen Schritt, bis ein Element in der Warteschlange verbleibt: der resultierende Pairing Heap.

Ein gutes Beispiel für den oben beschriebenen Prozess:

• Entfernen eines beliebigen Nicht-Root-Knotens Pairing Heap:
  
  Betrachten Sie den gelöschten Knoten als die Wurzel eines Teilbaums des ursprünglichen Heaps. Zuerst entfernen wir die Wurzel dieses Teilbaums, indem wir dem zuvor beschriebenen Algorithmus zum Entfernen der Wurzel des Pairing Heap folgen, und führen dann das Verfahren zum Zusammenführen des resultierenden Baums mit dem ursprünglichen Baum aus.
• Abrufen des minimalen Pairing Heap-Elements:
  
  Geben Sie einfach den Wert des Heap-Stamms zurück.

Unsere Bekanntschaft mit Pairing Heap endet jedoch nicht hier: Mit Pairing Heap können Sie einige Vorgänge nicht sofort ausführen, sondern nur dann, wenn sie benötigt werden. Mit anderen Worten, mit Pairing Heap können Sie Vorgänge "Lazily" ausführen und so die fortgeführten Anschaffungskosten einiger von ihnen senken.
Angenommen, wir haben K Einfügungen vorgenommen und K in Pairing Heap gelöscht. Offensichtlich wird das Ergebnis dieser Operationen nur dann notwendig, wenn wir das minimale Element vom Heap anfordern.
Betrachten wir, wie sich der Algorithmus der Aktionen der zuvor beschriebenen Operationen während ihrer Lazy-Implementierung ändert:

Unter Ausnutzung der Tatsache, dass die Kuchi-Wurzel mindestens zwei Nullzeiger hat, werden wir einen von ihnen verwenden, um den Kopf einer doppelt verknüpften Liste (im Folgenden auxList ) von Elementen darzustellen , die in den Heap eingefügt wurden, von denen jedes als die Wurzel eines unabhängigen Paarungshaufens betrachtet wird. Dann:

• Lazy Node Insertion in Pairing Heap:
  
  Wenn Sie den angegebenen U-Knoten in den Pairing Heap { R_1 , V_1 } einfügen, fügen Sie ihn in auxList ein - nach dem Kopf der Liste:

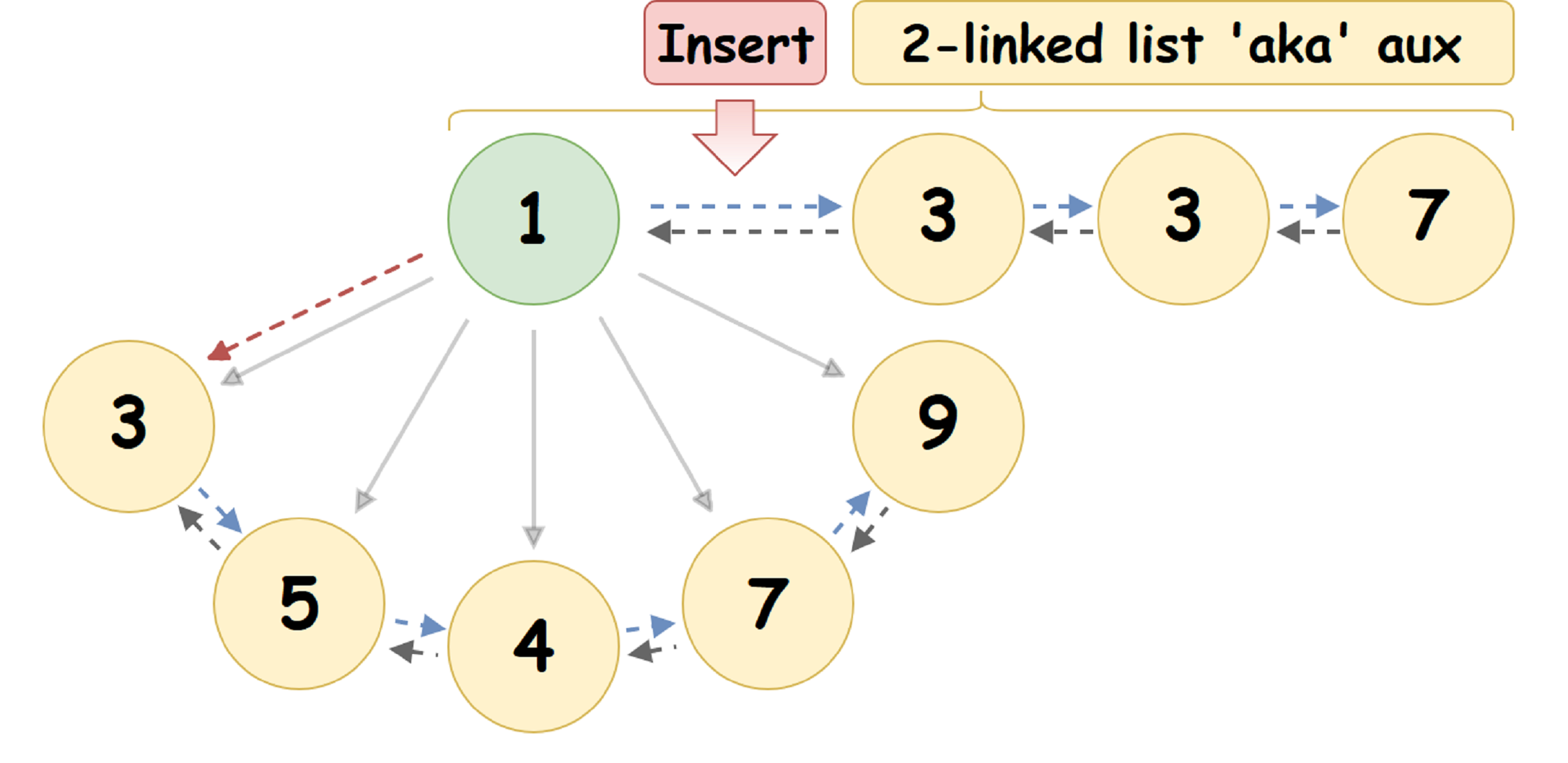
• Die faule Verschmelzung zweier Pairing Heap:
  
  Lazy Zusammenführen von zwei Pairing-Heaps, ähnlich wie beim Einfügen eines Lazy-Knotens, wobei der eingefügte Knoten die Wurzel (Kopf der doppelt verbundenen AuxList) eines der Heaps ist.
• Faul, das minimale Pairing Heap-Element zu erhalten:
  
  Wenn wir ein Minimum anfordern, gehen wir durch auxList zur Liste der Wurzeln des unabhängigen Pairing Heap, kombinieren die Elemente dieser Liste paarweise mit der Zusammenführungsoperation und geben den Wert des Stamms, der das Minimum-Element enthält, an einen der resultierenden Pairing Heap zurück.
• Faules Entfernen des minimalen Pairing Heap-Elements:
  
  Wenn Sie das Entfernen des vom Pairing Heap angegebenen Mindestelements anfordern, suchen wir zuerst den Knoten, der das Mindestelement enthält, und entfernen ihn dann aus dem Baum, in dem es sich um den Stamm handelt, und fügen seine Teilbäume in die AuxList des Hauptheaps ein.
• Verzögertes Entfernen eines beliebigen Nicht-Root-Pairing-Heap-Knotens:
  
  Beim Löschen eines beliebigen Nicht-Root-Pairing-Heap-Knotens wird der Knoten aus dem Heap entfernt und seine untergeordneten Knoten werden in die AuxList des Haupt-Heaps eingefügt.

Tatsächlich reduziert die Verwendung der Lazy Pairing Heap-Implementierung die amortisierten Kosten für das Einfügen und Entfernen beliebiger Knoten im Pairing Heap: von O (log N) auf O (1).

Das ist alles, und unten finden Sie eine Liste nützlicher Links und Ressourcen:

[0] JeMalloc Github Page
[1] Originalartikel über Pairing Heaps
[2] Originalartikel über Lazy Implementation Pairing Heaps
[3] Telegrammkanal über Codeoptimierungen, C ++, Asm, 'Low Level' und nichts weiter!

Fortsetzung folgt…