Maschinelles Lernen für Ihre Wohnungssuche. Teil 2

A. A. A. A. A. A. A. A. A. A. A. A. A. A.
Haben Sie über den Einfluss der nächstgelegenen U-Bahn auf den Preis Ihrer Wohnung nachgedacht? A. A.
A. A. A. A. Was ist mit mehreren Kindergärten in Ihrer Wohnung? Sind Sie bereit, in die Welt der Geodaten einzutauchen?

A. A. 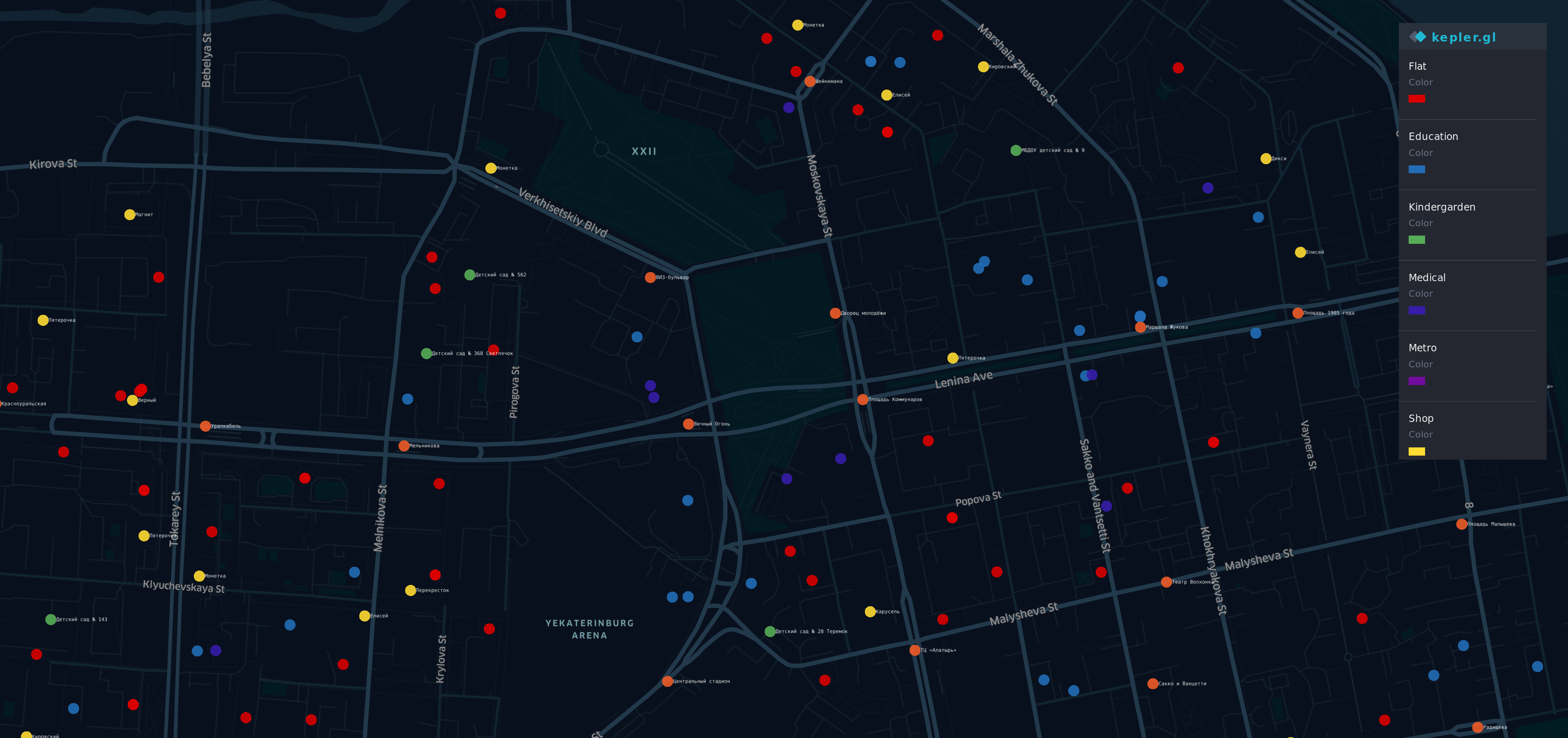A. A.
A. A. A. A.
A. A.

Worum geht es?

A. A.
Im vorigen Teil hatten wir einige Daten und haben versucht, ein ausreichend gutes Angebot auf einem Immobilienmarkt in Jekaterinburg zu finden.

Wir waren an einem Punkt angekommen, an dem wir eine Genauigkeit bei der Kreuzvalidierung nahe 73% hatten. Jede Münze hat jedoch 2 Seiten. Und 73% Genauigkeit sind 27% Fehler. Wie könnten wir das weniger machen? Was ist der nächste Schritt?

A. A.

Geodaten helfen dabei

Was ist mit mehr Daten aus der Umgebung? Wir können Geokontext und einige räumliche Daten verwenden.
A. A.
Selten verbringen Menschen ihr ganzes Leben zu Hause. A. A. Manchmal gehen sie in Geschäfte, nehmen Kinder aus der Kindertagesstätte. Ihre Kinder wachsen auf und gehen zur Schule, zur Universität usw. A. A.

Oder ... Manchmal brauchen sie medizinische Hilfe und suchen ein Krankenhaus. Und eine sehr wichtige Sache ist der öffentliche Verkehr, zumindest die U-Bahn. A. A. Mit anderen Worten, es gibt viele Dinge in der Nähe, die sich auf die Preisgestaltung auswirken.

Lassen Sie mich Ihnen eine Liste von ihnen zeigen:

• Öffentliche Verkehrsmittel halten an
• Geschäfte
• Kindergärten
• Krankenhäuser / medizinische Einrichtungen A. A. A. A. A. A. A. A. A. A. A. A. A. A. A. A. A. A.
• Bildungseinrichtungen A. A. A. A. A. A. A. A. A. A. A. A. A. A. A. A. A. A.
• U-Bahn

Visualisierung für neue Daten

Nachdem Sie diese Informationen erhalten haben A. A. Verschiedene Quellen A. A. A. A. Ich habe eine Visualisierung gemacht.

A. A.
A. A. A. A. A. A. A. A. A. A.
Es gibt einige Punkte auf der Karte, der prestigeträchtigste (und teuerste) Bezirk von Yek Aterinburg. A. A. A. A. A. A. A. A. A. A.
A. A. A. A.

• A. A. A. A. A. A. A. A. R ed Punkte - Wohnungen
• O lief ge - stoppt
• Gelbe Läden
• G reen - Kindergärten
• B lue - Bildung
• Ich ndigo - medizinisch
• V iolet - Metro

Ja, ein Regenbogen ist hier.

Übersicht

Jetzt haben wir einen Datensatz, der an Geodaten gebunden ist und einige neue Informationen enthält

df.head(10) 

 df.describe() 

Ein gutes altes Modell

Versuchen Sie es genauso wie zuvor

 y = df.cost X = df.drop(columns=['cost']) X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2,random_state=42) 

Dann trainieren wir unser Modell erneut, drücken die Daumen und versuchen erneut, den Preis für eine Wohnung vorherzusagen.

 from sklearn.linear_model import LinearRegression regressor = LinearRegression() model = regressor.fit(X_train, y_train) do_cross_validation(X_test, y_test, model) 

Hmm ... es sieht mit 73% Genauigkeit besser aus als das vorherige Ergebnis.
Was ist mit Interpretationsversuchen? Unser Vorgängermodell hatte eine ausreichende Fähigkeit, den Pauschalpreis zu erklären.

 estimate_model(regressor) 

Ups ... Unser neues Modell funktioniert gut mit alten Funktionen, aber das Verhalten mit neuen scheint seltsam.

Zum Beispiel führt die größere Anzahl von Bildungseinrichtungen oder medizinischen Einrichtungen zu einem Rückgang des Wohnungspreises. Dementsprechend ist die Anzahl der Haltestellen in der Nähe der Wohnung identisch und sollte einen zusätzlichen Beitrag zum Wohnungspreis leisten.
Das neue Modell ist genauer, passt aber nicht zum wirklichen Leben.

Etwas ist kaputt

Lassen Sie uns überlegen, was passiert ist.

Zunächst möchte ich Sie daran erinnern, dass das Hauptmerkmal unserer linearen Regression ... ähm ... Linearität ist. Ja, Captain Obvious ist hier.

Wenn Ihre Daten mit der Idee "Je größer / Leasing ist X, desto größer / Leasing wird Y" kompatibel sind, ist die lineare Regression ein gutes Werkzeug. Geodaten sind jedoch komplexer als erwartet.

Zum Beispiel:

• Wenn sich in der Nähe Ihrer Wohnung eine Bushaltestelle befindet, ist dies gut, aber wenn die Anzahl etwa 5 beträgt, führt dies zu einer lauten Straße, und die Leute möchten es vermeiden, eine Wohnung in der Nähe zu kaufen.
• Wenn es eine Universität gibt, sollte sie einen guten Einfluss auf den Preis haben.
  Gleichzeitig ist eine Menge von Studenten in Ihrer Nähe nicht so erfreut, wenn Sie keine sehr gesellige Person sind.
• Metro in der Nähe Ihres Hauses ist gut, aber wenn Sie in einer Stunde zu Fuß leben
  von der nächsten U-Bahn - es sollte keinen Sinn machen.

Wie Sie sehen, hängt es von vielen Faktoren und Gesichtspunkten ab. Und die Art unserer Geodaten ist nicht linear, wir können die Auswirkungen nicht extrapolieren.
Warum funktioniert ein Modell mit bizarren Koeffizienten gleichzeitig besser als das vorherige?

 plot.figure(figsize=(10,10)) corr = df.corr()*100.0 sns.heatmap(corr[['cost']], cmap= sns.diverging_palette(220, 10), center=0, linewidths=1, cbar_kws={"shrink": .7}, annot=True, fmt=".2f") 

Es sieht interessant aus. Wir haben das ähnliche Bild im vorherigen Teil gesehen.
Es besteht eine negative Korrelation zwischen der Entfernung zur nächsten U-Bahn und dem Preis. Und dieser Faktor wirkt sich mehr auf die Genauigkeit aus als einige ältere.

In der Zwischenzeit arbeitet unser Modell chaotisch und sieht keine Abhängigkeiten zwischen aggregierten Daten und Zielvariablen. Die Einfachheit der linearen Regression hat ihre eigenen Grenzen. A. A.

Der König ist tot, es lebe der König!

Und wenn eine lineare Regression für unseren Fall nicht geeignet ist, was kann besser sein? Wenn nur unser Modell "schlauer" sein könnte ...

Glücklicherweise haben wir einen Ansatz, der besser sein sollte, weil er flexibler ist und über einen eingebauten Mechanismus verfügt: "Mach das, wenn das das macht, sonst mach das".

Der Entscheidungsbaum wird in der Szene angezeigt.

 from sklearn.tree import DecisionTreeRegressor A decision tree can have a different depth, usually, it works well when depth is 3 and bigger. And the parameter of max depth has the biggest influence on the result. Let's do some code for checking depth from 3 to 32 data = [] for x in range(3,32): regressor = DecisionTreeRegressor(max_depth=x,random_state=42) model = regressor.fit(X_train, y_train) accuracy = do_cross_validation(X, y, model) data.append({'max_depth':x,'accuracy':accuracy}) data = pd.DataFrame(data) ax = sns.lineplot(x="max_depth", y="accuracy", data=data) max_result = data.loc[data['accuracy'].idxmax()] ax.set_title(f'Max accuracy-{max_result.accuracy}\nDepth {max_result.max_depth} ') 

Nun ... für eine Situation, in der die m A. A. Ax_depth eines Baumes ist gleich 8, die Genauigkeit liegt über 77.
Und es wäre eine gute Leistung, wenn wir nicht über die Grenzen dieses Ansatzes nachdenken würden. Lassen Sie uns einen Blick darauf werfen, wie es funktionieren wird A. A. A. A. M ax_depht = 2 A. A. A. A. A. A.

 from IPython.core.display import Image, SVG from sklearn.tree import export_graphviz from graphviz import Source 2_level_regressor = DecisionTreeRegressor(max_depth=2, random_state=42) model = 2_level_regressor.fit(X_train, y_train) graph = Source(export_graphviz(model, out_file=None , feature_names=X.columns , filled = True)) SVG(graph.pipe(format='svg')) 

Auf diesem Bild sehen wir, dass es nur 4 Varianten der Vorhersage gibt. Wenn Sie DecisionTreeRegressor verwenden , funktioniert es anders als die lineare Regression . Einfach anders. Es wird kein Beitrag von Faktoren (Koeffizienten) verwendet, stattdessen verwendet DecisionTreeRegressor "Likelihood". Und der Preis einer Wohnung wird der gleiche sein, den die vorhergesagte Wohnung am ähnlichsten hat.
Wir können es zeigen, indem wir unseren Preis mit diesem Baum vorhersagen.

 y = two_level_regressor.predict(X_test) errors = pd.DataFrame(data=y,columns=['errors']) f, ax = plot.subplots(figsize=(12, 12)) sns.countplot(x="errors", data=errors) 

Und jede Ihrer Vorhersagen stimmt mit einem dieser Werte überein. Und wenn wir max_depth = 8 verwenden, können wir nicht mehr als 256 verschiedene Optionen für mehr als 2000 Wohnungen erwarten. Vielleicht ist es gut für Klassifizierungsprobleme, aber es ist nicht flexibel genug für unseren Fall.

Weisheit der Menge

Wenn Sie versuchen, das Ergebnis im Finale der Weltmeisterschaft vorherzusagen, besteht eine große Wahrscheinlichkeit, dass Sie sich irren. Wenn Sie alle Richter der Meisterschaft um eine Meinung bitten, haben Sie gleichzeitig bessere Chancen zu erraten. Wenn Sie unabhängige Experten, Trainer, Richter fragen und dann mit Antworten zaubern, erhöhen sich Ihre Chancen erheblich. Sieht aus wie eine Wahl eines Präsidenten.

Ein Ensemble aus mehreren "primitiven" Bäumen kann mehr als jeder von ihnen geben. Und Rando mForestRegressor ist ein Werkzeug, das wir verwenden werden

Betrachten wir zunächst die grundlegenden Parameter - max_depth , max_features und eine Reihe von Bäumen im Modell.
A. A.

Anzahl der Bäume

In Übereinstimmung mit "Wie viele Bäume in einem zufälligen Wald?" Die beste Wahl sind 128 Bäume . Eine weitere Erhöhung der Anzahl der Bäume führt nicht zu einer signifikanten Verbesserung der Genauigkeit, sondern zu einer Verlängerung der Trainingszeit.

Maximale Anzahl von Funktionen

Derzeit verfügt unser Modell über 12 Funktionen. Die Hälfte von ihnen sind alte, die sich auf Merkmale der Wohnung beziehen, andere auf den Geokontext. Also habe ich beschlossen, jedem von ihnen eine Chance zu geben. Es seien 6 Merkmale für einen Baum.

Maximale Tiefe eines Baumes

Für diesen Parameter können wir eine Lernkurve analysieren.

 from sklearn.ensemble import RandomForestRegressor data = [] for x in range(1,32): regressor = RandomForestRegressor(random_state=42, max_depth=x, n_estimators=128,max_features=6)model = regressor.fit(X_train, y_train)accuracy = do_cross_validation(X, y, model) data.append({'max_depth':x,'accuracy':accuracy}) data = pd.DataFrame(data) f, ax = plot.subplots(figsize=(10, 10)) sns.lineplot(x="max_depth", y="accuracy", data=data) max_result = data.loc[data['accuracy'].idxmax()] ax.set_title(f'Max accuracy-{max_result.accuracy}\nDepth {max_result.max_depth} ') 

Whoa ... über 86% Genauigkeit bei max_depth = 16 gegenüber 77% bei einem Designbaum . Es sieht toll aus, nicht wahr?

Fazit

Nun ... jetzt haben wir ein besseres Vorhersageergebnis als die vorherigen, 86% stehen kurz vor dem Ziel. Der letzte Schritt zur Überprüfung - sehen wir uns die Wichtigkeit der Funktionen an. Haben Geodaten unserem Modell Vorteile gebracht?

 feat_importances = model.feature_importances_ feat_importances = pd.Series(feat_importances, index=X.columns) feat_importances.nlargest(5).plot(kind='barh') 

Einige alte Funktionen haben sich immer noch auf das Ergebnis ausgewirkt. Gleichzeitig hat sich auch die Entfernung zur nächsten U-Bahn und zu den Kindergärten ausgewirkt. Und es klingt logisch.

Ohne Zweifel haben uns Geodaten geholfen, unser Modell zu verbessern.

Danke fürs Lesen!

PS

Unsere Reise ist noch nicht beendet. Eine Genauigkeit von 86% ist ein enormes Ergebnis für reale Daten. Inzwischen gibt es eine kleine Lücke zwischen 14% und 10% des mittleren Fehlers, die wir erwarten. Im nächsten Kapitel unserer Geschichte werden wir versuchen, diese Barriere zu überwinden oder zumindest diesen Fehler zu verringern. A. A. A. A. A. A. A. A. A. A. A. A. A. A. A. A.

Da ist das IPython-Notebook