Navier-Stokes-Gleichung und Flüssigkeitssimulation auf CUDA

Hallo Habr. In diesem Artikel werden wir uns mit der Navier-Stokes-Gleichung für eine inkompressible Flüssigkeit befassen, sie numerisch lösen und eine schöne Simulation erstellen, die durch paralleles Rechnen auf CUDA funktioniert. Das Hauptziel ist es zu zeigen, wie Sie die der Gleichung zugrunde liegende Mathematik in der Praxis anwenden können, wenn Sie das Problem der Modellierung von Flüssigkeiten und Gasen lösen.




Hinweis: Wenn Sie den Habr von einem mobilen Gerät aus lesen und die Formeln nicht sehen, verwenden Sie die Vollversion der Website

Navier-Stokes-Gleichung für eine inkompressible Flüssigkeit

$$

$${\ teilweise {\ bf \ vec {u}} \ über {\ teilweise t}} = - ({\ bf \ vec {u}} \ cdot \ nabla) {\ bf \ vec {u}} - {1 \ over \ rho} \ nabla {\ bf p} + \ nu \ nabla ^ 2 {\ bf \ vec {u}} + {\ bf \ vec {F}}$$

Ich denke, jeder hat mindestens einmal von dieser Gleichung gehört, einige haben vielleicht sogar ihre speziellen Fälle analytisch gelöst, aber im Allgemeinen bleibt dieses Problem bis jetzt ungelöst. Natürlich setzen wir uns in diesem Artikel nicht das Ziel, das Millenniumsproblem zu lösen, aber wir können die iterative Methode trotzdem darauf anwenden. Aber für den Anfang schauen wir uns die Notation in dieser Formel an.

Herkömmlicherweise kann die Navier-Stokes-Gleichung in fünf Teile unterteilt werden:

• $$$\ teilweise {\ bf \ vec {u}} \ über \ teilweise t$ - bezeichnet die Änderungsrate der Flüssigkeitsgeschwindigkeit an einem Punkt (wir werden sie für jedes Partikel in unserer Simulation berücksichtigen).
• $$$- ({\ bf \ vec {u}} \ cdot \ nabla) {\ bf \ vec {u}}$ - die Bewegung von Flüssigkeit im Raum.
• $$$- {1 \ over \ rho} \ nabla {\ bf p}$ Wird der Druck auf das Partikel ausgeübt (hier? $$$\ rho$ - Flüssigkeitsdichtekoeffizient).
• $$$\ nu \ nabla ^ 2 {\ bf \ vec {u}}$ - Viskosität des Mediums (je größer es ist, desto stärker widersteht die Flüssigkeit der auf sein Teil ausgeübten Kraft), $$$\ nu$ - Viskositätskoeffizient).
• $$$\ bf \ vec {F}$ - externe Kräfte, die wir auf die Flüssigkeit ausüben (in unserem Fall spielt die Kraft eine ganz bestimmte Rolle - sie spiegelt die vom Benutzer ausgeführten Aktionen wider.

Da wir den Fall einer inkompressiblen und homogenen Flüssigkeit betrachten werden, haben wir auch eine andere Gleichung: $$${{\ \ nabla \ cdot \ bf \ vec {u}} = 0}$ . Die Energie in der Umwelt ist konstant, geht nirgendwo hin, kommt nicht von irgendwoher.

Es ist falsch, alle Leser, die mit der Vektoranalyse nicht vertraut sind, gleichzeitig zu berauben und kurz alle in der Gleichung vorhandenen Operatoren durchzugehen (ich empfehle jedoch dringend, sich an die Ableitung, das Differential und den Vektor zu erinnern, da sie all dem zugrunde liegen was weiter unten besprochen wird).

Wir beginnen mit dem Nabla-Operator, der ein solcher Vektor ist (in unserem Fall ist er zweikomponentig, da wir die Flüssigkeit im zweidimensionalen Raum modellieren):

$$

$$\ nabla = {\ begin {pmatrix} {\ partiell \ über \ partiell x}, {\ partiell \ über \ partiell y} \ end {pmatrix}}$$

Der Nabla-Operator ist ein Vektordifferentialoperator und kann sowohl auf eine Skalarfunktion als auch auf eine Vektorfunktion angewendet werden. Im Fall eines Skalars erhalten wir den Gradienten der Funktion (den Vektor ihrer partiellen Ableitungen) und im Fall eines Vektors die Summe der partiellen Ableitungen entlang der Achsen. Das Hauptmerkmal dieses Operators ist, dass Sie damit die Hauptoperationen der Vektoranalyse ausdrücken können - grad ( Gradient ), div ( Divergenz ), rot ( Rotor ) und $$$\ nabla ^ 2$ ( Laplace-Operator ). Es ist sofort erwähnenswert, dass der Ausdruck $$$({\ bf \ vec {u} \ cdot \ nabla}) {\ bf \ vec {u}}$ nicht gleichbedeutend mit $$$({\ nabla \ cdot \ bf \ vec {u}}) {\ bf \ vec {u}}$ - Der Nabla-Operator hat keine Kommutativität.

Wie wir später sehen werden, werden diese Ausdrücke merklich vereinfacht, wenn Sie sich in einen diskreten Raum bewegen, in dem wir alle Berechnungen durchführen. Seien Sie also nicht beunruhigt, wenn Sie im Moment nicht genau wissen, was Sie mit all dem tun sollen. Nachdem wir die Aufgabe in mehrere Teile unterteilt haben, werden wir sie nacheinander lösen und all dies in Form der sequentiellen Anwendung mehrerer Funktionen auf unsere Umgebung präsentieren.

Numerische Lösung der Navier-Stokes-Gleichung

Um unsere Flüssigkeit im Programm darzustellen, müssen wir zu einem beliebigen Zeitpunkt eine mathematische Darstellung des Zustands jedes Flüssigkeitsteilchens erhalten. Die bequemste Methode hierfür besteht darin, ein Vektorfeld von Partikeln zu erstellen, die ihren Zustand in Form einer Koordinatenebene speichern:



In jeder Zelle unseres zweidimensionalen Arrays speichern wir jeweils die Partikelgeschwindigkeit $$$t: {\ bf \ vec {u}} = u ({\ bf \ vec {x}}, t), \ bf \ vec {x} = \ begin {pmatrix} x, y \ end {pmatrix}$ und der Abstand zwischen Teilchen wird mit bezeichnet $$$\ delta x$ und $$$\ delta y$ entsprechend. Im Code reicht es aus, den Geschwindigkeitswert bei jeder Iteration zu ändern und einen Satz mehrerer Gleichungen zu lösen.

Jetzt drücken wir den Gradienten, die Divergenz und den Laplace-Operator unter Berücksichtigung unseres Koordinatengitters aus ( $$$i, j$ - Indizes im Array, $$$\ bf \ vec {u} _ {(x)}, \ vec {u} _ {(y)}$ - Entnehmen der entsprechenden Komponenten aus dem Vektor):

Wir können die diskreten Formeln von Vektoroperatoren weiter vereinfachen, wenn wir dies annehmen $$$\ delta x = \ delta y = 1$ . Diese Annahme hat keinen großen Einfluss auf die Genauigkeit des Algorithmus, verringert jedoch die Anzahl der Operationen pro Iteration und macht Ausdrücke im Allgemeinen für das Auge angenehmer.

Partikelbewegung

Diese Aussagen funktionieren nur, wenn wir die nächstgelegenen Teilchen relativ zu den derzeit betrachteten finden können. Um alle möglichen Kosten aufzuheben, die mit dem Finden dieser Kosten verbunden sind, werden wir nicht ihre Bewegung verfolgen, sondern woher die Partikel zu Beginn der Iteration kommen, indem wir die Bewegungsbahn zeitlich rückwärts projizieren (mit anderen Worten, subtrahieren Sie den Geschwindigkeitsvektor mal die Zeitänderung von aktuelle Position). Mit dieser Technik für jedes Element des Arrays können wir sicher sein, dass jedes Partikel „Nachbarn“ hat:



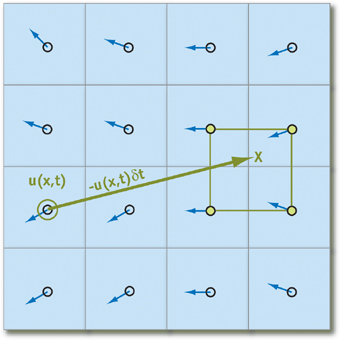
Das setzen $$$q$ - Als Array-Element, das den Zustand des Partikels speichert, erhalten wir die folgende Formel zur Berechnung seines Zustands über die Zeit $$$\ delta t$ (Wir glauben, dass alle notwendigen Parameter in Form von Beschleunigung und Druck bereits berechnet wurden):

$$

$$q ({{\ \ vec {\ bf x}}, t + \ delta t}) = q ({{\ \ bf \ vec {x}} - {\ bf \ vec {u}} \ delta t}, t)$$

Wir stellen sofort fest, dass für ausreichend kleine $$$\ delta t$ und wir können niemals über die Grenzen der Zelle hinausgehen, daher ist es sehr wichtig, den richtigen Impuls zu wählen, den der Benutzer den Partikeln gibt.

Um einen Genauigkeitsverlust bei einer Projektion an der Zellgrenze oder bei nicht ganzzahligen Koordinaten zu vermeiden, führen wir eine bilineare Interpolation der Zustände der vier nächsten Teilchen durch und nehmen sie als den wahren Wert an einem Punkt. Im Prinzip wird eine solche Methode die Genauigkeit der Simulation praktisch nicht verringern, und gleichzeitig ist sie recht einfach zu implementieren, sodass wir sie verwenden werden.

Viskosität

Jede Flüssigkeit hat eine bestimmte Viskosität, die Fähigkeit, den Einfluss äußerer Kräfte auf ihre Teile zu verhindern (Honig und Wasser sind ein gutes Beispiel, in einigen Fällen unterscheiden sich ihre Viskositätskoeffizienten um eine Größenordnung). Die Viskosität wirkt sich direkt auf die von der Flüssigkeit erfasste Beschleunigung aus und kann durch die folgende Formel ausgedrückt werden, wenn wir der Kürze halber für eine Weile andere Begriffe weglassen:

$$

$${\ partielle \ vec {\ bf u} \ über \ partielle t} = {\ nu \ nabla ^ 2 \ bf \ vec {u}}$$

. In diesem Fall hat die iterative Geschwindigkeitsgleichung die folgende Form:

$$

$$u ({\ bf \ vec {x}}, t + \ delta t) = u ({\ bf \ vec {x}}, t) + \ nu \ delta t \ nabla ^ 2 \ bf \ vec {u }$$

Wir werden diese Gleichheit leicht transformieren und in die Form bringen $$$\ bf A \ vec {x} = \ vec {b}$ (Standardform eines linearen Gleichungssystems):

$$

$$({\ bf I} - \ nu \ delta t \ nabla ^ 2) u ({\ bf \ vec {x}}, t + \ delta t) = {u ({\ bf \ vec {x}}, t )}$$

wo $$$\ bf I$ Ist die Identitätsmatrix. Wir brauchen solche Transformationen, um anschließend die Jacobi-Methode anzuwenden, um mehrere ähnliche Gleichungssysteme zu lösen. Wir werden es auch später besprechen.

Externe Kräfte

Der einfachste Schritt des Algorithmus ist das Aufbringen externer Kräfte auf das Medium. Für den Benutzer wird dies in Form von Klicks auf dem Bildschirm mit der Maus oder ihrer Bewegung wiedergegeben. Die äußere Kraft kann durch die folgende Formel beschrieben werden, die wir für jedes Element der Matrix anwenden ( $$$\ vec {\ bf G}$ - Impulsvektor $$$x_p, y_p$ - Mausposition $$$x, y$ - Koordinaten der aktuellen Zelle, $$$r$ - Aktionsradius, Skalierungsparameter):

$$

$$\ vec {\ bf F} = \ vec {\ bf G} \ Delta t {\ bf exp} \ left (- {{(x - x_p) ^ 2 + (y - y_p) ^ 2} \ over r} \ rechts)$$

Ein Impulsvektor kann leicht als Differenz zwischen der vorherigen Position der Maus und der aktuellen Position (falls vorhanden) berechnet werden, und hier können Sie immer noch kreativ sein. In diesem Teil des Algorithmus können wir das Hinzufügen von Farben zu einer Flüssigkeit, ihre Beleuchtung usw. einführen. Externe Kräfte können auch Schwerkraft und Temperatur umfassen, und obwohl es nicht schwierig ist, solche Parameter zu implementieren, werden wir sie in diesem Artikel nicht berücksichtigen.

Druck

Der Druck in der Navier-Stokes-Gleichung ist die Kraft, die verhindert, dass Partikel den gesamten ihnen zur Verfügung stehenden Raum ausfüllen, nachdem sie eine externe Kraft auf sie ausgeübt haben. Die Berechnung ist sofort sehr schwierig, aber unser Problem kann durch Anwendung des Helmholtz-Zerlegungssatzes erheblich vereinfacht werden.

Rufen Sie an $$$\ bf \ vec {W}$ Vektorfeld nach Berechnung von Verschiebung, äußeren Kräften und Viskosität. Es wird eine Divergenz ungleich Null aufweisen, was dem Zustand der Inkompressibilität der Flüssigkeit widerspricht ( $$$\ nabla \ cdot \ bf \ vec {u} = 0$ ), und um dies zu beheben, ist es notwendig, den Druck zu berechnen. Nach dem Helmholtz-Zerlegungssatz, $$$\ bf \ vec {W}$ kann als die Summe von zwei Feldern dargestellt werden:

$$

$$\ bf \ vec {W} = \ vec {u} + \ nabla p$$

wo $$$\ bf u$ - Dies ist das Vektorfeld, das wir ohne Divergenz suchen. In diesem Artikel wird kein Beweis für diese Gleichheit erbracht, aber am Ende finden Sie einen Link mit einer detaillierten Erklärung. Wir können den Nabla-Operator auf beide Seiten des Ausdrucks anwenden, um die folgende Formel zur Berechnung des Skalardruckfelds zu erhalten:

$$

$$\ nabla \ cdot \ bf \ vec {W} = \ nabla \ cdot (\ vec {u} + \ nabla p) = \ nabla \ cdot \ vec {u} + \ nabla ^ 2 p = \ nabla ^ 2 p$$

Der oben geschriebene Ausdruck ist die Poisson-Gleichung für Druck. Wir können es auch mit der oben genannten Jacobi-Methode lösen und dadurch die letzte unbekannte Variable in der Navier-Stokes-Gleichung finden. Im Prinzip können lineare Gleichungssysteme auf verschiedene und ausgefeilte Arten gelöst werden, aber wir werden uns noch mit den einfachsten befassen, um diesen Artikel nicht weiter zu belasten.

Rand- und Anfangsbedingungen

Jede Differentialgleichung, die auf einer endlichen Domäne modelliert ist, erfordert korrekt spezifizierte Anfangs- oder Randbedingungen, andernfalls erhalten wir sehr wahrscheinlich ein physikalisch falsches Ergebnis. Randbedingungen werden festgelegt, um das Verhalten der Flüssigkeit in der Nähe der Kanten des Koordinatengitters zu steuern, und die Anfangsbedingungen geben die Parameter an, die die Partikel zum Zeitpunkt des Programmstarts haben.

Die Anfangsbedingungen sind sehr einfach - anfangs ist die Flüssigkeit stationär (Partikelgeschwindigkeit ist Null) und der Druck ist ebenfalls Null. Die Randbedingungen für Geschwindigkeit und Druck werden durch die angegebenen Formeln festgelegt:

$$

$${\ bf \ vec {u} _ {0, j} + \ bf \ vec {u} _ {1, j} \ über 2 \ delta y} = 0, {\ bf \ vec {u} _ {i , 0} + \ bf \ vec {u} _ {i, 1} \ über 2 \ delta x} = 0$$

$$

$${\ bf p_ {0, j} - \ bf p_ {1, j} \ über \ delta x} = 0, {\ bf p_ {i, 0} - \ bf p_ {i, 1} \ über \ delta y} = 0$$

Somit ist die Geschwindigkeit der Partikel an den Kanten der Geschwindigkeit an den Kanten entgegengesetzt (wodurch sie sich von der Kante abstoßen), und der Druck ist gleich dem Wert unmittelbar neben der Grenze. Diese Operationen sollten auf alle Begrenzungselemente des Arrays angewendet werden (z. B. gibt es eine Rastergröße $$$N \ mal M$ , dann wenden wir den Algorithmus für Zellen an, die in der Abbildung blau markiert sind):

Farbstoff

Mit dem, was wir jetzt haben, können Sie sich bereits viele interessante Dinge einfallen lassen. Zum Beispiel, um die Ausbreitung von Farbstoff in einer Flüssigkeit zu realisieren. Dazu müssen wir nur ein weiteres Skalarfeld beibehalten, das für die Farbmenge an jedem Punkt der Simulation verantwortlich ist. Die Formel zum Aktualisieren des Farbstoffs ist der Geschwindigkeit sehr ähnlich und wird ausgedrückt als:

$$

$${\ partielles d \ über \ partielles t} = {- (\ vec {\ bf u} \ cdot \ nabla) d} + \ gamma \ nabla ^ 2d + S$$

In der Formel $$$S$ verantwortlich für das Auffüllen des Bereichs mit einem Farbstoff (möglicherweise abhängig davon, wo der Benutzer klickt), $$$d$ direkt ist die Menge an Farbstoff am Punkt und $$$\ gamma$ - Diffusionskoeffizient. Die Lösung ist nicht schwierig, da bereits alle grundlegenden Arbeiten zur Ableitung von Formeln durchgeführt wurden und es ausreicht, einige Substitutionen vorzunehmen. Paint kann im Code als Farbe im RGB-Format implementiert werden. In diesem Fall wird die Aufgabe auf Operationen mit mehreren realen Werten reduziert.

Vorticity

Die Vorticity-Gleichung ist kein direkter Bestandteil der Navier-Stokes-Gleichung, aber ein wichtiger Parameter für eine plausible Simulation der Bewegung eines Farbstoffs in einer Flüssigkeit. Aufgrund der Tatsache, dass wir einen Algorithmus auf einem diskreten Feld erzeugen, sowie aufgrund von Verlusten bei der Genauigkeit von Gleitkommawerten geht dieser Effekt verloren, und daher müssen wir ihn wiederherstellen, indem wir auf jeden Punkt im Raum zusätzliche Kraft anwenden. Der Vektor dieser Kraft wird als bezeichnet $$$\ bf \ vec {T}$ und wird durch die folgenden Formeln bestimmt:

$$

$$\ bf \ omega = \ nabla \ times \ vec {u}$$

$$

$$\ vec {\ eta} = \ nabla | \ omega |$$

$$

$$\ bf \ vec {\ psi} = {\ vec {\ eta} \ über {| \ vec {\ eta} |}}$$

$$

$$\ bf \ vec {T} = \ epsilon (\ vec {\ psi} \ times \ omega) \ delta x$$

$$$\ omega$ es gibt das Ergebnis der Anwendung des Rotors auf den Geschwindigkeitsvektor (seine Definition ist am Anfang des Artikels angegeben), $$$\ vec \ eta$ - Gradient des Skalarfeldes der Absolutwerte $$$\ omega$ . $$$\ vec \ psi$ repräsentiert einen normalisierten Vektor $$$\ vec \ eta$ und $$$\ epsilon$ Ist eine Konstante, die steuert, wie groß die Wirbel in unserer Flüssigkeit sein werden.

Jacobi-Methode zur Lösung linearer Gleichungssysteme

Bei der Analyse der Navier-Stokes-Gleichungen haben wir zwei Gleichungssysteme entwickelt - eines für die Viskosität und eines für den Druck. Sie können durch einen iterativen Algorithmus gelöst werden, der durch die folgende iterative Formel beschrieben werden kann:

$$

$$x ^ {(k + 1)} _ {i, j} = {{x ^ {(k)} _ {i-1, j} + x ^ {(k)} _ {i + 1, j} + x ^ {(k)} _ {i, j-1} + x ^ {(k)} _ {i, j + 1} + \ alpha b_ {i, j}} \ over \ beta}$$

Für uns $$$x$ - Array-Elemente, die ein Skalar- oder Vektorfeld darstellen. $$$k$ - Die Iterationsnummer können wir anpassen, um die Genauigkeit der Berechnung zu erhöhen, oder umgekehrt, um sie zu reduzieren und die Produktivität zu steigern.

Um die Viskosität zu berechnen, ersetzen wir: $$$x = b = \ bf \ vec {u}$ , $$$\ alpha = {1 \ over \ nu \ delta t}$ , $$$\ beta = 4+ \ alpha$ Hier ist der Parameter $$$\ beta$ - die Summe der Gewichte. Daher müssen wir mindestens zwei Vektorgeschwindigkeitsfelder speichern, um die Werte eines Feldes unabhängig voneinander zu lesen und in ein anderes zu schreiben. Für die Berechnung des Geschwindigkeitsfeldes nach der Jacobi-Methode müssen im Durchschnitt 20-50 Iterationen durchgeführt werden, was ziemlich viel ist, wenn wir Berechnungen an der CPU durchgeführt haben.

Für die Druckgleichung nehmen wir folgende Substitution vor: $$$x = p$ , $$$b = \ nabla \ bf \ cdot \ vec {W}$ , $$$\ alpha = -1$ , $$$\ beta = 4$ . Als Ergebnis erhalten wir den Wert $$$p_ {i, j} \ delta t$ an der Stelle. Da es jedoch nur zur Berechnung des vom Geschwindigkeitsfeld subtrahierten Gradienten verwendet wird, können zusätzliche Transformationen weggelassen werden. Für das Druckfeld ist es am besten, 40-80 Iterationen durchzuführen, da bei kleineren Zahlen die Diskrepanz spürbar wird.

Implementierung des Algorithmus

Wir werden den Algorithmus in C ++ implementieren, wir benötigen auch das Cuda Toolkit (Sie können lesen, wie es auf der Nvidia-Website installiert wird) sowie SFML . Wir benötigen CUDA, um den Algorithmus zu parallelisieren, und SFML wird nur verwendet, um ein Fenster zu erstellen und ein Bild auf dem Bildschirm anzuzeigen (Im Prinzip kann dies in OpenGL geschrieben werden, aber der Leistungsunterschied ist nicht signifikant, aber der Code erhöht sich um weitere 200 Zeilen).

Cuda Toolkit

Zunächst werden wir ein wenig darüber sprechen, wie Sie mit dem Cuda Toolkit Aufgaben parallelisieren können. Eine detailliertere Anleitung wird von Nvidia selbst bereitgestellt, daher beschränken wir uns hier nur auf das Notwendigste. Es wird auch davon ausgegangen, dass Sie den Compiler installieren und ein Testprojekt ohne Fehler erstellen konnten.

Um eine Funktion zu erstellen, die auf der GPU ausgeführt wird, müssen Sie zunächst angeben, wie viele Kernel wir verwenden möchten und wie viele Kernelblöcke wir zuweisen müssen. Zu diesem Zweck bietet uns das Cuda Toolkit eine spezielle Struktur - dim3 . Standardmäßig werden alle x-, y- und z-Werte auf 1 gesetzt. Durch Angabe als Argument beim Aufrufen der Funktion können wir die Anzahl der zugewiesenen Kernel steuern. Da wir mit einem zweidimensionalen Array arbeiten, müssen wir im Konstruktor nur zwei Felder festlegen: x und y :

dim3 threadsPerBlock(x_threads, y_threads); dim3 numBlocks(size_x / x_threads, y_size / y_threads); 

Dabei sind size_x und size_y die Größe des zu verarbeitenden Arrays. Die Signatur und der Funktionsaufruf lauten wie folgt (dreifache spitze Klammern werden vom Cuda-Compiler verarbeitet):

 void __global__ deviceFunction(); // declare deviceFunction<<<numBlocks, threadsPerBlock>>>(); // call from host 

In der Funktion selbst können Sie die Indizes eines zweidimensionalen Arrays über die Blocknummer und die Kernelnummer in diesem Block mithilfe der folgenden Formel wiederherstellen:

 int x = blockIdx.x * blockDim.x + threadIdx.x; int y = blockIdx.y * blockDim.y + threadIdx.y; 

Es ist zu beachten, dass die auf der Grafikkarte ausgeführte Funktion mit dem Tag __global__ gekennzeichnet sein und auch void zurückgeben muss. Daher werden die Berechnungsergebnisse meistens in das als Argument übergebene Array geschrieben und im Speicher der Grafikkarte vorab zugewiesen.

Die Funktionen CudaMalloc und CudaFree sind für die Freigabe und Zuweisung von Speicher auf der Grafikkarte verantwortlich. Wir können Zeiger auf den Speicherbereich bearbeiten, den sie zurückgeben, aber wir können nicht über den Hauptcode auf die Daten zugreifen. Der einfachste Weg, die Berechnungsergebnisse zurückzugeben, ist die Verwendung von cudaMemcpy , ähnlich dem Standard- memcpy , jedoch in der Lage, Daten von einer Grafikkarte in den Hauptspeicher und umgekehrt zu kopieren.

SFML und Fenster rendern

Mit all diesem Wissen können wir endlich direkt Code schreiben. Erstellen Sie zunächst die Datei main.cpp und platzieren Sie den gesamten Hilfscode für das Fenster-Rendering dort:


Zeile am Anfang der Hauptfunktion

 std::vector<sf::Uint8> pixelBuffer(FIELD_WIDTH * FIELD_HEIGHT * 4); 

Erstellt ein RGBA-Bild in Form eines eindimensionalen Arrays mit konstanter Länge. Wir werden es zusammen mit anderen Parametern ( Mausposition , Differenz zwischen Frames) an die Funktion computeField übergeben . Letztere sowie mehrere andere Funktionen werden in kernel.cu deklariert und rufen den auf der GPU ausgeführten Code auf. Auf der SFML-Website finden Sie Dokumentation zu allen Funktionen. Im Dateicode passiert nichts sehr Interessantes, sodass wir hier nicht lange aufhören werden.

GPU-Computing

Um Code unter gpu zu schreiben, erstellen Sie zunächst eine kernel.cu-Datei und definieren Sie darin mehrere Hilfsklassen: Color3f, Vec2, Config, SystemConfig :


Das Attribut __host__ vor dem Methodennamen bedeutet, dass der Code auf der CPU ausgeführt werden kann. __Device__ verpflichtet den Compiler im Gegenteil, Code unter der GPU zu sammeln. Der Code deklariert Grundelemente für die Arbeit mit Zweikomponentenvektoren, Farbe, Konfigurationen mit Parametern, die zur Laufzeit geändert werden können, sowie mehrere statische Zeiger auf Arrays, die wir als Puffer für Berechnungen verwenden.

cudaInit und cudaExit sind ebenfalls recht trivial definiert:


In der Initialisierungsfunktion weisen wir Speicher für zweidimensionale Arrays zu, geben ein Array von Farben an, mit denen die Flüssigkeit gemalt wird, und legen die Standardwerte in der Konfiguration fest. In cudaExit geben wir einfach alle Puffer frei. So paradox es auch klingen mag, zum Speichern zweidimensionaler Arrays ist es am vorteilhaftesten, eindimensionale Arrays zu verwenden, auf die mit dem folgenden Ausdruck zugegriffen wird:

 array[y * size_x + x]; // equals to array[y][x] 

Wir beginnen die Implementierung des direkten Algorithmus mit der Partikelverschiebungsfunktion. Die Felder oldField und newField (das Feld, aus dem die Daten stammen und in das sie geschrieben werden), die Größe des Arrays sowie das Zeitdelta und der Dichtekoeffizient (die verwendet werden, um die Auflösung des Farbstoffs in der Flüssigkeit zu beschleunigen und das Medium nicht sehr empfindlich für Advect zu machen, werden an Advect übertragen Benutzeraktionen). Die bilineare Interpolationsfunktion wird auf klassische Weise durch die Berechnung von Zwischenwerten implementiert:


Es wurde beschlossen, die Viskositätsdiffusionsfunktion in mehrere Teile zu unterteilen: computeDiffusion wird aus dem Hauptcode aufgerufen, der diffuse und computeColor eine vorgegebene Anzahl von Malen aufruft , und dann das Array vertauscht , von dem wir die Daten nehmen, und dasjenige, in das wir sie schreiben. Dies ist der einfachste Weg, um eine parallele Datenverarbeitung zu implementieren, aber wir verbrauchen doppelt so viel Speicher.

Beide Funktionen verursachen Variationen der Jacobi-Methode. Der Hauptteil von jacobiColor und jacobiVelocity überprüft sofort, ob sich die aktuellen Elemente nicht an der Grenze befinden. In diesem Fall müssen wir sie gemäß den im Abschnitt Rand- und Anfangsbedingungen beschriebenen Formeln festlegen.


Die Anwendung externer Kraft wird durch eine einzige Funktion implementiert - applyForce , die die Position der Maus, die Farbe des Farbstoffs und auch den Aktionsradius als Argument verwendet. Mit seiner Hilfe können wir den Partikeln Geschwindigkeit verleihen und sie malen. Mit dem brüderlichen Exponenten können Sie den Bereich nicht zu scharf und gleichzeitig im angegebenen Radius ganz klar machen.


Die Berechnung der Vorticity ist bereits ein komplexerer Prozess, daher implementieren wir sie in computeVorticity und applyVorticity . Wir stellen außerdem fest, dass für sie zwei solche Vektoroperatoren wie Curl (Rotor) und absGradient (Gradient der absoluten Feldwerte) definiert werden müssen. Um zusätzliche Wirbeleffekte festzulegen, multiplizieren wir $$$y$ Komponente des Gradientenvektors auf $$$-1$ und normalisieren Sie es dann durch Teilen durch die Länge (ohne zu vergessen, dass der Vektor ungleich Null ist):


Der nächste Schritt im Algorithmus ist die Berechnung des Skalardruckfeldes und seiner Projektion auf das Geschwindigkeitsfeld. Dazu müssen wir 4 Funktionen implementieren: Divergenz , die die Geschwindigkeitsdivergenz berücksichtigt, jacobiPressure , das die Jacobi-Methode für Druck implementiert, und computePressure mit computePressureImpl , das iterative Feldberechnungen durchführt:


Die Projektion passt in zwei kleine Funktionen - Projekt und Gradient , die Druck erfordern. Dies ist die letzte Stufe unseres Simulationsalgorithmus:


Nach der Projektion können wir sicher mit dem Rendern des Bildes im Puffer und verschiedenen Posteffekten fortfahren. Die Malfunktion kopiert Farben aus dem Partikelfeld in das RGBA-Array. Die Funktion applyBloom wurde ebenfalls implementiert, die die Flüssigkeit hervorhebt, wenn der Cursor darauf platziert und die Maustaste gedrückt wird. Erfahrungsgemäß macht diese Technik das Bild für die Augen des Benutzers angenehmer und interessanter, ist aber überhaupt nicht notwendig.

In der Nachbearbeitung können Sie auch Stellen hervorheben, an denen die Flüssigkeit die höchste Geschwindigkeit aufweist, die Farbe je nach Bewegungsvektor ändern, verschiedene Effekte hinzufügen usw. In unserem Fall beschränken wir uns jedoch auf eine Art Minimum, da die Bilder selbst damit sehr faszinierend sind (insbesondere in Bezug auf die Dynamik). ::


Und am Ende haben wir noch eine Hauptfunktion, die wir von main.cpp aufrufen - computeField . Es verknüpft alle Teile des Algorithmus, ruft den Code auf der Grafikkarte auf und kopiert auch die Daten von GPU zu CPU. Es enthält auch die Berechnung des Impulsvektors und die Wahl der Farbstofffarbe, die wir an applyForce übergeben :

Fazit

In diesem Artikel haben wir einen numerischen Algorithmus zur Lösung der Navier-Stokes-Gleichung analysiert und ein kleines Simulationsprogramm für eine inkompressible Flüssigkeit geschrieben. Vielleicht haben wir nicht alle Feinheiten verstanden, aber ich hoffe, dass sich das Material als interessant und nützlich für Sie herausstellte und zumindest als gute Einführung in das Gebiet der Fluidmodellierung diente.

Als Autor dieses Artikels freue ich mich über Kommentare und Ergänzungen und werde versuchen, alle Ihre Fragen unter diesem Beitrag zu beantworten.

Zusätzliches Material

Sie finden den gesamten Quellcode in diesem Artikel in meinem Github-Repository . Verbesserungsvorschläge sind willkommen.

Das Originalmaterial, das als Grundlage für diesen Artikel diente, finden Sie auf der offiziellen Nvidia-Website. Es werden auch Beispiele für die Implementierung von Teilen des Algorithmus in der Sprache der Shader vorgestellt:
developer.download.nvidia.com/books/HTML/gpugems/gpugems_ch38.html

Der Beweis des Helmholtz-Zerlegungssatzes und eine große Menge zusätzlichen Materials zur Strömungsmechanik finden Sie in diesem Buch (Englisch, siehe Abschnitt 1.2):
Chorin, AJ und JE Marsden. 1993. Eine mathematische Einführung in die Strömungsmechanik. 3rd ed. Springer .

Der Kanal eines englischsprachigen YouTube, der qualitativ hochwertige Inhalte in Bezug auf Mathematik und insbesondere die Lösung von Differentialgleichungen (Englisch) erstellt. Sehr visuelle Videos, die helfen, die Essenz vieler Dinge in Mathematik und Physik zu verstehen:
3Blue1Brown - YouTube-
Differentialgleichungen (3Blue1Brown)

Ich danke auch WhiteBlackGoose für die Hilfe bei der Vorbereitung des Materials für den Artikel.

---

Und am Ende ein kleiner Bonus - ein paar schöne Screenshots aus dem Programm:


Direkter Stream (Standardeinstellungen)


Whirlpool (großer Radius in applyForce)


Welle (hohe Vorticity + Diffusion) Auf vielfachen

Wunsch habe ich auch ein Video mit der Simulation hinzugefügt: