Hallo habrozhiteli! Wir haben kürzlich Chris Bernhards
Buch Quantum Computing for Real IT übergeben . Hier beschlossen sie, einen Auszug aus dem Buch "Grovers Algorithmus und Datensuche" zu teilen.
Wir treten in die Ära von Big Data ein. Das effiziente Durchsuchen gigantischer Datensätze ist derzeit für viele große Unternehmen ein brennendes Problem. Der Algorithmus von Grover ist theoretisch in der Lage, das Abrufen von Daten zu beschleunigen.
Love Grover erfand seinen Algorithmus 1996. Wie die Algorithmen von Deutsch und Simon hat es eine höhere Ausführungsgeschwindigkeit im Vergleich zu klassischen Algorithmen hinsichtlich der Komplexität der Abfragen. Wir können den aktuellen Datenabrufalgorithmus jedoch nicht ohne Orakel implementieren, die ihre Fragen stellen könnten. Wir müssen einen Algorithmus konstruieren, der die Arbeit des Orakels ausführt. Bevor wir jedoch über die Implementierung des Grover-Algorithmus sprechen, wollen wir uns ansehen, was und wie er funktioniert.
Grover-Algorithmus
Stellen Sie sich vor, Sie haben vier Spielkarten. Sie sind auf den Kopf gestellt. Sie wissen, dass einer von ihnen ein Ass von Würmern ist und Sie müssen es finden. Wie viele Karten müssen Sie umdrehen, bis Sie wissen, wo das Ass der Würmer liegt?
Wenn Sie Glück haben, finden Sie die gewünschte Karte beim ersten Versuch. Wenn Sie kein Glück haben, können Sie drei Karten umdrehen, und keine davon ist ein Ass der Würmer. Im schlimmsten Fall, wenn Sie drei Karten umdrehen, wissen Sie sicher, dass die letzte Karte das Ass des Wurms ist, nach dem Sie suchen. So können wir herausfinden, wo sich das Ass befindet, indem wir von einer auf drei Karten wechseln. Im Durchschnitt müssen Sie 2,25 Karten umdrehen.
Dies ist eine der Aufgaben, die der Grover-Algorithmus löst. Bevor wir mit der Beschreibung des Algorithmus beginnen, formulieren wir das Problem neu. Wir haben vier binäre Sequenzen: 00, 01, 10 und 11. Wir haben eine Funktion f, die für drei dieser Sequenzen 0 und für die vierte Sequenz 1 zurückgibt. Wir müssen die Binärsequenz finden, die dem Ausgabewert 1 entspricht. Beispielsweise können wir die folgenden Ergebnisse erhalten: f (00) = 0, f (01) = 0, f (10) = 1 und f (11) = 0. Nun ist das Problem ist herauszufinden, wie oft die Funktion berechnet werden sollte, um das Ergebnis f (10) = 1 zu erhalten. Hier haben wir das Problem einfach neu formuliert, indem wir Spielkarten durch Funktionen ersetzt haben, sodass die Antwort auf diese Frage bereits bekannt ist: Nach wie vor ist es im Durchschnitt erforderlich, die Funktion zu berechnen 2,25 mal.
Wie bei allen Algorithmen für Komplexitätsabfragen konstruieren wir ein Orakel - ein Gate, das eine Funktion kapselt. Das Orakel für unser Beispiel, in dem es nur vier Binärsequenzen gibt, ist in Abb. 1 dargestellt. 9.1.
Die Kette für den Grover-Algorithmus ist in Abb. 2 dargestellt. 9.2.
Der Algorithmus führt zwei Schritte aus. Beim ersten Mal wird das Vorzeichen der Wahrscheinlichkeitsamplitude umgedreht, verbunden mit dem Ort, den wir suchen. Die zweite verstärkt diese Wahrscheinlichkeitsamplitude. Mal sehen, wie die Kette das macht.
Nach der Übertragung durch die Hadamard-Ventile erhalten die beiden oberen Qubits den Zustand
und das untere Qubit hat einen Zustand
Der kombinierte Zustand kann geschrieben werden als
Die Qubits passieren dann Gate F. Es invertiert 0 und 1 im dritten Qubit zu dem Ort, den wir suchen. Für unseren Fall f (10) = 1 erhalten wir
Es kann umgeschrieben werden als
Als Ergebnis erhalten wir zwei obere Qubits, die nicht mit den unteren, sondern mit der Wahrscheinlichkeitsamplitude verwechselt werden
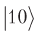
ändert das Vorzeichen und zeigt den gewünschten Ort an.
Wenn wir in diesem Schritt die oberen beiden Qubits messen, erhalten wir eine von vier Stellen, und alle vier möglichen Antworten sind gleich wahrscheinlich. Wir müssen einen weiteren Schritt tun - um die Wahrscheinlichkeitsamplitude zu erhöhen. Die Amplifikation erfolgt durch Umkehren der Zahlenfolge relativ zu ihrem Durchschnitt. Wenn die Zahl über dem Durchschnitt liegt, dreht sie sich um und wird unterdurchschnittlich. Wenn die Zahl unterdurchschnittlich ist, dreht sie sich um und wird überdurchschnittlich. In jedem Fall bleibt die Entfernung vom Durchschnitt erhalten. Zur Veranschaulichung verwenden wir vier Zahlen: 1, 1, 1 und –1. Ihre Summe ist 2 und der Durchschnitt ist 2/4 oder 1/2. Dann beginnen wir, die Zahlen in der Reihenfolge zu sortieren. Die erste Zahl ist 1. Sie liegt 1/2 über dem Durchschnitt. Nach dem Putsch sollte es 1/2 niedriger als der Durchschnitt sein. In diesem Fall wird es zu 0. Die Zahl –1 liegt um 3/2 unter dem Durchschnitt. Nach dem Putsch sollte er 3/2 über dem Durchschnitt liegen, dh 2 werden.
Zwei obere Qubits haben derzeit einen Zustand
Wenn wir die Amplituden relativ zum Durchschnitt drehen, erhalten wir

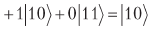
.
Nach Abschluss der Messung erhalten wir definitiv 10, dh eine Umdrehung im Verhältnis zum Durchschnitt gibt uns genau das, was wir brauchen. Alles, was wir tun müssen, ist sicherzustellen, dass es ein Tor oder, was auch immer, eine orthogonale Matrix gibt, die eine Umdrehung relativ zum Durchschnitt beschreibt. Eine solche Matrix existiert:
Durch die Wirkung des Ventils auf die oberen beiden Qubits erhalten wir
In diesem Beispiel, in dem wir nur zwei Qubits haben, sollten wir das Orakel nur einmal verwenden. Es reicht uns, die einzige Frage zu stellen. Für den Fall n = 2 gibt der Grover-Algorithmus nach einer einzelnen Frage eine genaue Antwort, während im klassischen Fall durchschnittlich 2,25 Fragen gestellt werden müssen.
Diese Idee erstreckt sich auf den Fall einer beliebigen Anzahl von n Qubits. Wir beginnen mit dem Drehen des Vorzeichens der Wahrscheinlichkeitsamplitude, die dem gewünschten Ort entspricht. Dann führen wir eine Revolution relativ zum Durchschnitt durch. In diesem Fall tritt die Verstärkung der Amplitude jedoch nicht so signifikant auf wie in der Situation mit zwei Qubits. Nehmen wir zum Beispiel acht Zahlen, von denen sieben 1 und eine -1 sind. Ihre Summe ist 6 und der Durchschnitt ist 6/8. Nach einem Flip wird die durchschnittliche 1 1/2 und –1 10/4. Infolgedessen erhalten wir bei Vorhandensein von drei Qubits, die ein Qubit nach Verstärkung der Amplitude messen, den gewünschten Ort mit einer höheren Wahrscheinlichkeit als andere. Das Problem ist, dass es eine erhebliche Chance gibt, die falsche Antwort zu erhalten. Wir brauchen eine höhere Wahrscheinlichkeit, die richtige Antwort zu erhalten - wir müssen die Amplitude vor dem Messen weiter verstärken. Die Lösung besteht darin, alle Qubits durch die Kette zurück zu übertragen. Wir drehen erneut das Vorzeichen der Wahrscheinlichkeitsamplitude, die dem gewünschten Ort zugeordnet ist, und drehen erneut relativ zum Durchschnitt.
Betrachten Sie den verallgemeinerten Fall. Wir müssen etwas an einem der m möglichen Orte finden. Um es auf klassische Weise zu finden, müssen wir im schlimmsten Fall m - 1 Fragen stellen. Die Anzahl der Fragen wächst proportional zu m. Grover berechnete eine Formel, die bestimmt, wie oft seine Kette verwendet werden muss, um die maximale Wahrscheinlichkeit einer korrekten Antwort zu erhalten. Die Zahl, die diese Formel angibt, wächst proportional
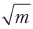
. Dies ist eine quadratische Beschleunigung.
Grover-Algorithmus-Anwendungen
Es gibt mehrere Probleme bei der Implementierung des Algorithmus. Zunächst wird die quadratische Beschleunigung relativ zur Komplexitätsanforderung bewertet. Um das Orakel zu verwenden, müssen Sie es erstellen. Wenn Sie diese Aufgabe nicht mit der gebotenen Sorgfalt ausführen, überwiegt die Anzahl der vom Orakel ausgeführten Schritte die Anzahl der vom Algorithmus gespeicherten Schritte. Infolgedessen wird der Algorithmus langsamer als schneller als der klassische. Ein weiteres Problem besteht darin, dass wir durch Bestimmen der Beschleunigung annehmen, dass der Datensatz ungeordnet ist. Wenn der Datensatz eine bestimmte Struktur hat, finden Sie häufig einen klassischen Algorithmus, der diese Struktur verwendet und viel schneller nach einer Lösung sucht. Das letzte Problem betrifft die Beschleunigung. Die quadratische Beschleunigung ist nichts anderes als eine exponentielle Beschleunigung, die wir bei anderen Algorithmen beobachtet haben. Kann man mehr erreichen? Schauen wir uns diese Themen an.
Beide Probleme, die mit der Implementierung des Orakels und dem Vorhandensein der Struktur im Datensatz verbunden sind, sind gerechtfertigt und zeigen, dass der Grover-Algorithmus in den meisten Fällen keine praktische Anwendung zum Durchsuchen der Datenbank hat. In einigen Situationen ermöglicht es eine Struktur in den Daten, ein Orakel zu erstellen, das mit hoher Effizienz agiert. In solchen Situationen kann der Algorithmus klassische Algorithmen überholen. Die Antwort auf die Frage nach der Möglichkeit eines größeren Erfolgs wurde bereits gegeben. Es ist bewiesen, dass der Grover-Algorithmus optimal ist. Es gibt keinen Quantenalgorithmus, der ein Problem mit mehr als einer quadratischen Beschleunigung lösen kann. Die quadratische Beschleunigung ist zwar nicht so beeindruckend wie die exponentielle, bietet jedoch einige Vorteile. Bei der Arbeit mit großen Datenmengen kann jede Beschleunigung hilfreich sein.
Es ist wahrscheinlich, dass der Grover-Algorithmus die Hauptanwendung nicht für die Suche findet, wie oben dargestellt, sondern für ihre Variationen. Insbesondere kann die Idee der Verstärkung der Amplitude nützlich sein.
Wir haben nur einige wenige Algorithmen untersucht, aber die Shore- und Grover-Algorithmen werden als die wichtigsten angesehen. Es gibt viele andere Algorithmen, die auf den Ideen dieser beiden basieren.1 Lassen Sie uns nun unsere Aufmerksamkeit von Quantenalgorithmen auf andere Anwendungsbereiche des Quantencomputers richten.