Hallo allerseits! Mein Name ist Dmitry Rudnev, ich bin Frontend-Entwickler bei BCS. Ich begann meine Reise mit dem Layout von Schnittstellen unterschiedlicher Komplexität und achtete immer besonders auf die Benutzeroberfläche: Wie angenehm wäre es für den Benutzer, mit ihm zu interagieren, wenn ich dem Benutzer genau die Benutzeroberfläche vermitteln könnte, die der Designer beabsichtigt hatte.
In dieser Artikelserie möchte ich meine Erfahrungen mit der Anwendung funktionaler Praktiken in der Frontend-Entwicklung teilen. Ich werde über die Vor- und Nachteile sprechen, die Sie als Entwickler mit diesen Praktiken erhalten. Wenn Ihnen das Thema gefällt, tauchen wir in die „trockeneren“ und komplexeren Ecken der Funktionswelt ein. Ich stelle sofort fest, dass wir von größer zu kleiner wechseln werden, das heißt, wir werden die klassische Anwendung aus der Vogelperspektive betrachten, und während wir die Artikel durchgehen, werden wir dahin gehen, wo bestimmte Praktiken uns spürbare Vorteile bringen.
Beginnen wir also mit dem Umgang mit den Zuständen. Gleichzeitig werde ich Ihnen und hier im Allgemeinen Monaden und Funktoren erzählen.
Intro
Als ich die nächste Schnittstelle entwirrte und Gemeinsamkeiten zwischen der Benutzeroberfläche und der Analyse fand, bemerkte ich, dass ein Entwickler jedes Mal, wenn er sich mit einem Netzwerk befasst, nur alle Benutzeroberflächenzustände verarbeiten und die Reaktion auf einen bestimmten Zustand beschreiben muss. Und da jeder von uns nach Spitzenleistungen strebt, besteht der Wunsch, dass diese Art der Verarbeitung von Zuständen ein Muster hervorbringt, das so transparent wie möglich beschreibt, was geschieht und was der Auslöser einer bestimmten Reaktion und damit das Ergebnis der Arbeit ist. Glücklicherweise wurde in der Welt der Programmierung fast alles, was Sie sich vorstellen können, von jemandem vor Ihnen implementiert.
Sowohl in der Entwicklungswelt als auch in der Designwelt wurden nicht nur Muster gebildet, mit denen Sie Ihre Probleme effektiv lösen können, sondern auch Antipatter, die auf jeden Fall vermieden werden sollten, damit schlechte Praktiken nicht gedeihen und der Entwickler oder Designer in Situationen immer Fuß fassen konnte. wenn es keine konkrete Lösung gibt.
In unserem Fall ist die Situation, die die meisten Entwickler haben, die Verarbeitung aller Zustände des UI-Elements und die Reaktion darauf. Das Problem hierbei ist, dass das UI-Element sowohl mit dem lokalen Status (ohne asynchrone Anforderungen) als auch mit Remote-Ressourcen oder Repositorys interagieren kann. Entwickler vergessen manchmal, alle Randfälle zu behandeln, was zu einem inkonsistenten Verhalten des gesamten Systems führt.
Alle Beispiele enthalten Codebeispiele, die die React-Bibliothek und eine Obermenge von JavaScript - TypeScript verwenden, sowie Bibliotheken für die funktionale Programmierung von fp-ts.
Stellen Sie sich das einfachste Beispiel vor, in dem wir eine Liste von Elementen haben, die wir vom Server anfordern, und die Benutzeroberfläche entsprechend dem Ergebnis der Anforderung korrekt anzeigen müssen. Wir sind an der
render interessiert, da wir darin den korrekten Status während der Ausführung der Anfrage anzeigen müssen. Der vollständige Beispielcode kann unter folgender Adresse eingesehen werden:
einfache Anwendung . In Zukunft wird es ein komplettes Projekt geben, das sich auf eine Reihe von Artikeln konzentriert, in denen wir im Verlauf die einzelnen Teile zerlegen werden.
const renderInitial = (...) => ...; const renderPending = (...) => ...; const renderError = (...) => ... ; const renderSuccess = (...) => ... ; return ( {state.subcribers.foldL( renderInitial, renderPending, renderError, renderSuccess, )} );
Das Beispiel zeigt deutlich, dass jeder Status des Datenmodells eine eigene Funktion hat und jede Funktion ein Fragment der ihm vorgeschriebenen Benutzeroberfläche zurückgibt (Nachricht, Schaltfläche usw.). Mit Blick auf die Zukunft werde ich sagen, dass das Beispiel
RemoteData monad .
Das ist so elegant und vor allem sicher, dass wir mit Daten arbeiten und darauf reagieren können. Dies war die Einführung, in der ich versuchte, die Vorteile eines funktionalen Ansatzes in einem so scheinbar einfachen Beispiel zu demonstrieren.
Funktor und Monade
Lassen Sie uns nun schrittweise in die angewandte Kategorietheorie eintauchen und Konzepte wie
Functor und
Monad analysieren sowie Praktiken für die sichere Arbeit mit Daten unter Verwendung funktionaler Praktiken betrachten.
„Im Wesentlichen ist ein Funktor nichts anderes als eine Datenstruktur, mit der Sie Transformationsfunktionen anwenden können, um Werte aus einer Shell zu extrahieren, sie zu ändern und sie dann wieder in die Shell einzufügen.
Das Einschließen von Werten in eine Shell oder einen Container ist ein grundlegendes Entwurfsmuster in der funktionalen Programmierung, da es vor direktem Zugriff auf Werte schützt und diese in Anwendungsprogrammen sicher und unverändert manipuliert werden kann. “Ich habe dieses Zitat aus einem wunderbaren
Buch über die Überprüfung funktionaler Programmiertechniken in JavaScript entnommen . Beginnen wir mit der theoretischen Komponente und analysieren, was ein Funktor eigentlich ist. Zunächst müssen wir uns mit einem faszinierenden Teil der Mathematik vertraut machen, der als Kategorietheorie auf der grundlegendsten Ebene bezeichnet wird.
Die Kategorietheorie ist ein Zweig der Mathematik, der die Eigenschaften von Beziehungen zwischen mathematischen Objekten unabhängig von der internen Struktur von Objekten untersucht. Die Kategorietheorie nimmt in der modernen Mathematik einen zentralen Platz ein und hat auch Anwendungen in der Informatik, Logik und theoretischen Physik gefunden.Eine Kategorie besteht aus Objekten und Pfeilen, die zwischen ihnen gerichtet sind. Der einfachste Weg, eine Kategorie zu visualisieren, ist:
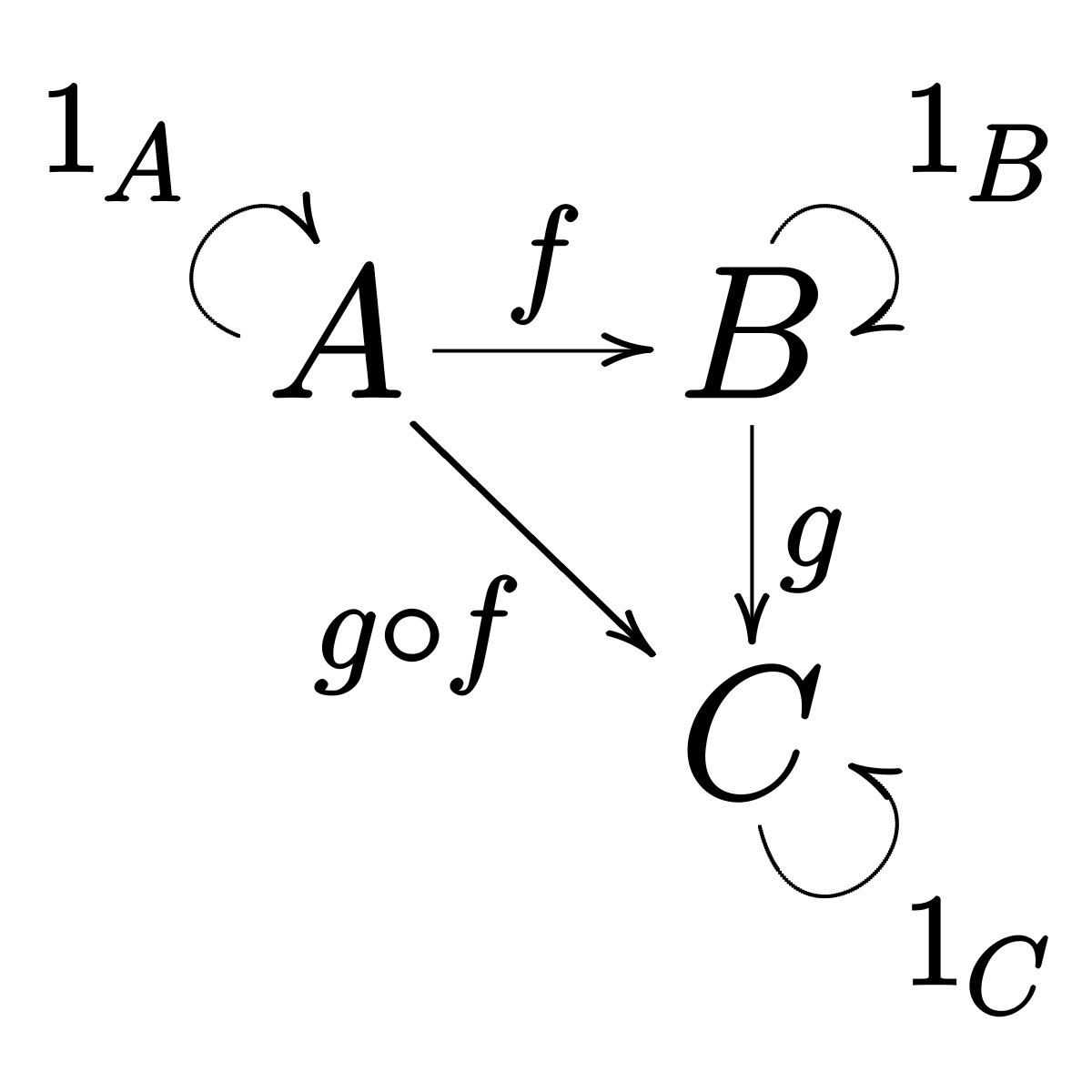
Die Pfeile sind so angeordnet, dass, wenn Sie einen Pfeil von Objekt
A zu Objekt
B und einen Pfeil von Objekt
B zu
C haben , ein Pfeil vorhanden sein muss - ihre Zusammensetzung reicht von
A nach
C. Stellen Sie sich Pfeile als Funktionen vor. Sie werden auch Morphismen genannt. Sie haben eine Funktion
f , die A als Argument verwendet und B zurückgibt. Es gibt eine andere Funktion
g , die B als Argument verwendet und C zurückgibt. Sie können sie kombinieren, indem Sie das Ergebnis von
f an
g . Wir haben gerade eine neue Funktion beschrieben, die A nimmt und C zurückgibt. In der Mathematik wird eine solche Zusammensetzung durch einen kleinen Kreis zwischen der Funktionsnotation bezeichnet: g ◦ f. Achten Sie auf die Kompositionsreihenfolge - von rechts nach links.
In der Mathematik ist die Komposition von rechts nach links gerichtet. In diesem Fall ist es hilfreich, wenn Sie g ◦ f als „g nach f“ lesen.
-— A B f :: A -> B -— B g :: B -> C -— A C g . f
Es gibt zwei sehr wichtige Eigenschaften, die eine Zusammensetzung in jeder Kategorie erfüllen muss.
- Die Zusammensetzung ist assoziativ (Assoziativität ist eine Eigenschaft von Operationen, mit der Sie die Reihenfolge ihrer Ausführung ohne explizite Angabe der Nachfolge mit gleicher Priorität wiederherstellen können. Dabei wird zwischen linker Assoziativität, bei der der Ausdruck von links nach rechts ausgewertet wird, und rechter Assoziativität von rechts nach links unterschieden. Die entsprechenden Operatoren werden als linksassoziativ und rechtsassoziativ bezeichnet Wenn Sie drei Morphismen (Pfeile) haben, f, g und h, die angeordnet werden können (dh ihre Typen stimmen überein), sind Sie sie braucht Klammern zu gruppieren. Mathematisch wird dies wie folgt geschrieben
h ◦ (g ◦ f) = (h ◦ g) ◦ f = h ◦ g ◦ f (h ◦ g) ◦ f = h ◦ g ◦ f - Für jedes Objekt A gibt es einen Pfeil, der eine Kompositionseinheit darstellt. Dieser Pfeil ist von einem Objekt zu sich selbst. Eine Kompositionseinheit zu sein bedeutet, dass beim Komponieren einer Einheit mit einem Pfeil, der entweder auf A beginnt oder auf A endet, die Komposition denselben Pfeil zurückgibt. Der Einheitspfeil eines Objekts A heißt IDa (Einheit auf A). Wenn in der mathematischen Notation f von A nach B geht, dann ist
f ◦ idA = f
Um mit Funktionen zu arbeiten, wird ein einzelner Pfeil als identische Funktion implementiert, die einfach ihr Argument zurückgibt.
Jetzt können wir überlegen, was ein Funktor in der Kategorietheorie ist.
Ein Funktor ist eine spezielle Art der Zuordnung zwischen Kategorien. Es kann als eine Anzeige verstanden werden, die die Struktur bewahrt. Die Funktoren zwischen kleinen Kategorien sind Morphismen in der Kategorie der kleinen Kategorien. Die Gesamtheit aller Kategorien ist keine Kategorie im üblichen Sinne, da die Gesamtheit ihrer Objekte keine Klasse ist. -
Wikipedia .
Stellen Sie sich eine Beispielimplementierung eines Funktors für den Vielleicht-Container vor, bei der es sich um die Idee eines „Werts handelt, der möglicherweise fehlt“.
const compose = <A, B, C>( f: (a: A) => B, g: (b: B) => C, ): (a: A) => C => (a: A) => g(f(a)); // Maybe: type Nothing = Readonly<{ tag: 'Nothing' }>; type Just<A> = Readonly<{ tag: 'Just'; value: A }>; export type Maybe<A> = Nothing | Just<A>; const nothing: Nothing = { tag: 'Nothing' }; const just = <A>(value: A): Just<A> => ({ tag: 'Just', value }); // Maybe: const fmap = <A, B>(f: (a: A) => B) => (fa: Maybe<A>): Maybe<B> => { switch (fa.tag) { case 'Nothing': return nothing; case 'Just': return just(f(fa.value)); } }; // 1: fmap id === id namespace Laws { console.log( fmap(id)(just(42)), id(just(42)), ); // => { tag: 'Just', value: 42 } // 2: fmap f ◦ fmap g === fmap (f ◦ g) const f = (a: number): string => `Got ${a}!`; const g = (s: string): number => s.length; console.log( compose(fmap(f), fmap(g))(just(42)), fmap(compose(f, g))(just(42)), ); // => { tag: 'Just', value: 7 } }
Die
fmap Methode kann von zwei Seiten betrachtet werden:
- Um eine reine Funktion auf einen "containerisierten" Wert anzuwenden;
- Um eine reine Funktion in den Containerkontext zu „heben“.
Wenn sich die Klammern in der Benutzeroberfläche geringfügig unterscheiden, können wir die Signatur der Funktion
fmap :
const fmap: <A, B>(f: (a: A) => B) => ((ma: Maybe<A>) => Maybe<B>);
Nachdem Sie die Schnittstelle definiert haben:
type Function1<Domain, Codomain> = (a: Domain) => Codomain;
wir bekommen die Definition von
fmap :
const fmap: <A, B>(f: (a: A) => B) => Function1<Maybe<A>, Maybe<B>>;
Dieser einfache Trick ermöglicht es uns, uns einen Funktor als eine Möglichkeit vorzustellen, „eine reine Funktion in einen Containerkontext zu heben“. Dank dessen ist es möglich, auf sichere Weise mit verschiedenen Arten von Daten zu arbeiten: Zum Beispiel erfolgreich Ketten von optionalen verschachtelten Werten verarbeiten; Datenlisten konvertieren Ausnahmen behandeln und mehr.
Wie bereits erläutert, können Sie mit Funktoren Funktionen sicher und unveränderlich auf Werte anwenden. Monaden ähneln Funktoren, können jedoch in besonderen Fällen spezielle Logik delegieren. Der Funktor selbst weiß nur, wie er diese Funktion anwendet und das Ergebnis wieder in eine Shell einwickelt, und er hat keine zusätzliche Logik.
Eine Monade entsteht beim Erstellen eines gesamten Datentyps nach dem Prinzip des Extrahierens von Daten nach dem Prinzip des Extrahierens von Werten aus Shells und des Definierens von Regeln aus dem Verschachteln. Monaden sind wie Funktoren eine Entwurfsvorlage, mit der Berechnungen in Form einer Abfolge von Stufen beschrieben werden, bei denen der verarbeitete Wert überhaupt nicht bekannt ist. Es sind jedoch die Monaden, die es ermöglichen, den Datenfluss sicher und ohne Nebenwirkungen zu steuern, wenn sie in der Komposition verwendet werden. Monaden können darauf abzielen, eine Vielzahl von Problemen zu lösen. Theoretisch hängen Monaden vom Typensystem in einer bestimmten Sprache ab. Tatsächlich denken viele Menschen, dass sie nur verstanden werden können, wenn es explizite Datentypen gibt.
Um Monaden besser zu verstehen, müssen die folgenden wichtigen Konzepte gelernt werden.
Monade Bietet eine abstrakte Schnittstelle für monadische Operationen
Monadischer Typ. Spezifische Implementierung dieser Schnittstelle
Aber praktische Beispiele für die Anwendung dieser Eigenschaften eines Funktors und anderer kategorialer Konstruktionen werde ich in zukünftigen Artikeln zeigen.