Über Schwerpunktkoordinaten an den Fingern

Hallo.

Sicherlich hat jeder zufällig eine Gucklochbewertung des Grads der Ähnlichkeit des Kindes mit den Eltern gesehen: so etwas wie "gegossener Vater, aber er sieht auch aus wie Mutter !!!"


( von hier genommen )

Wie im Beispiel im Bild können Sie den Ähnlichkeitsgrad in Prozent bewerten. Sie können auch Verwandte verwenden, um das Gesicht des Babys in Form einer gewichteten Summe von Verwandten von Verwandten genauer zu beschreiben ...

Und es wird für einen „normalen“ Menschen, der nicht mit Anthropologie oder beispielsweise Forensik in Verbindung gebracht wird, ganz natürlich aussehen und wahrgenommen werden. Für einen Fachmann auf dem Gebiet der Analyse und Gesichtserkennung ist ein menschliches Gesicht eher eine Reihe von Parametern. Das heißt, ein Punkt (ein Satz von Koordinaten) in einem Raum mit einer Basis (Achsen, die den Parametern entsprechen). Und wenn wir das Gesicht des Kindes im Vergleich zu seinen Verwandten beschreiben, wird höchstwahrscheinlich der Punkt, der dem Gesicht des Kindes entspricht, in diesem Parameterraum innerhalb der konvexen Hülle der Punktwolke erscheinen, die den Gesichtern der nächsten Angehörigen entspricht (dies ist jedoch nicht genau).

Worum geht es mir eigentlich? Diese beiden Ansätze zur Beschreibung von Gesichtern entsprechen zwei Koordinatensystemen:

1. baryzentrisch, Beschreibung eines Punktes im Raum (in unserem Beispiel: Gesicht) durch eine gewichtete Mischung anderer Punkte;
2. affin, eine Beschreibung eines Punktes im Raum durch Koordinaten in irgendeiner Basis.

Was sind also baryzentrische Koordinaten?

Lass rein -dimensionaler Raum gegeben Punkt mit Radiusvektoren , . Darüber hinaus liegt keiner der Punkte in der linearen Schale der Radiusvektoren der verbleibenden Punkte ... Einfach ausgedrückt ist es ganz einfach: Lassen Sie diese Punkte eine Figur bilden, die in einem Raum mit einer Dimension von weniger als nicht vollständig dargestellt werden kann .

Im Fall eines eindimensionalen Raums (Linie) benötigen wir 2 nicht zusammenfallende Punkte, im Fall eines zweidimensionalen Raums - ein nicht entartetes Dreieck, im Fall eines dreidimensionalen Raums - ein Tetraeder.

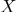
Dann jeder Punkt im Raum kann durch einen Radiusvektor dargestellt werden ::



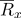
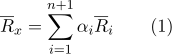
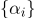
Stellen Sie ein und es gibt baryzentrische Koordinaten.

Wie sind baryzentrische Koordinaten besser / schlechter als affin?

Beginnen wir mit den relativen Nachteilen:

1. in der baryzentrischen Darstellung brauchen wir eine Koordinate mehr als in der affinen;
2. Der Abstand zwischen baryzentrisch angegebenen Punkten kann in diesen Koordinaten nicht direkt berechnet werden.

Zum Teil wird der erste Nachteil durch die Tatsache ausgeglichen, dass trotz der Notwendigkeit zu verwenden Schwerpunktkoordinaten bei der Beschreibung eines Punktes in -Dimensionaler Raum, die Anzahl der Grad erhöht sich nicht. Die in Formel (1) definierten Schwerpunktkoordinaten hängen durch die Beziehung zusammen:



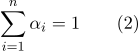
Was den zweiten Nachteil betrifft, ist es sinnvoll, Skalarprodukte zu berechnen, wenn der Abstand zwischen baryzentrisch dargestellten Punkten berechnet werden muss und benutze das Analogon der Mahalanobis-Distanz.

Was sind die Boni bei der Verwendung von Schwerpunktkoordinaten?

1. Baryzentrische Koordinaten sind unveränderlich für affine Raumtransformationen. Diese Eigenschaft wird beispielsweise für die lineare Interpolation in Computergrafiken verwendet. Lassen Sie Texturkoordinaten an den Eckpunkten eines dreieckigen Oberflächenelements definiert werden 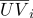und Normalen ( 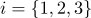), dann hat jeder Punkt dieses Oberflächenabschnitts Schwerpunktkoordinaten 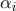seine Texturkoordinaten 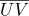und normal 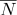kann berechnet werden als:
   
   
   
   
   
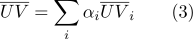
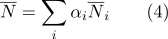
2. Anhand von Schwerpunktkoordinaten lässt sich leicht feststellen, ob ein Punkt dazu gehört 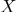Teile des Raumes, die von einem Polyeder mit Eckpunkten begrenzt werden : Dies wird nur gemacht, wenn . Die Gleichheit der i-ten Schwerpunktkoordinate 1 bedeutet, dass der Punkt fällt mit zusammen . Wenn mehrere Schwerpunktkoordinaten gleich 0 sind, bedeutet dies, dass der Punkt zu einem Unterraum gehört, der von den Radiusvektoren der verbleibenden Punkte überspannt wird, deren entsprechende Koordinaten größer als 0 sind.

Vielleicht sind sie sehr schwer zu berechnen?

Nicht komplizierter als eine lineare Transformation des Koordinatensystems. Denn im Wesentlichen ist die Berechnung von Schwerpunktkoordinaten eine solche Transformation.

Wir schreiben den Radiusvektor von Punkten in der folgenden Form neu:

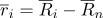
wo - ein radialer Vektor im Koordinatensystem, der an einem Punkt zentriert ist .

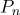
Dann kann Formel (1) in der folgenden Form umgeschrieben werden:



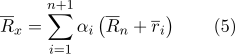
Wir werden die Klammern in der Summe offenbaren:



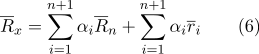
Nach Eigenschaft (2):



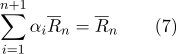
Dementsprechend:

,

wo

Angesichts von (2) beschränken wir uns auf die Berechnung der ersten n Schwerpunktkoordinaten. Stellen Sie sich den Übergang zu Schwerpunktkoordinaten als lineare Transformation vor:

,

wo - Vektor n der Schwerpunktkoordinaten (außer dem letzten), - Transformationsmatrix.

Angesichts der Eigenschaften der baryzentrischen Darstellung, wenn als Ersetzen Sie einen der Vektoren ( ), dann erhalten wir einen Vektor mit null Komponenten, mit Ausnahme einer i-ten, die gleich 1 ist.

Wenn die Matrix mit Matrix multiplizieren bestehend aus Spalten aus , dann sollten wir die Identitätsmatrix erhalten (eine Matrix mit Einsen auf der Hauptdiagonale und Nullen in den verbleibenden Elementen):

,

wo , Ist die Identitätsmatrix ( - Kronecker-Symbol: 1 wenn sonst 0).

Aus (10) finden wir ::



Somit mit einer Menge von Punkten mit Radiusvektoren , Wir können die Matrix berechnen, um sie in Schwerpunktkoordinaten umzuwandeln:



Mit dieser Matrix können wir die erste erhalten Schwerpunktkoordinaten mit Radiusvektor ::



Unter erneuter Verwendung der Beziehung (2) erhalten wir die letzte Schwerpunktkoordinate:

Fazit

Vielleicht wirkt der Schwerpunkt auf den ersten Blick auch umständlich und komplex. Tatsächlich ist dies jedoch ein sehr praktisches und unverzichtbares Werkzeug für viele Aufgaben, an das Sie sich ziemlich schnell gewöhnen. Da es hier keine Magie gibt, ist es lineare Algebra in ihrer reinsten Form!