Lineare Regression und Gradientenabstieg

Lassen Sie X- und Y-Indikatoren, die einen quantitativen Ausdruck haben, in einem bestimmten Themenbereich untersucht werden.

Darüber hinaus gibt es allen Grund zu der Annahme, dass der Indikator Y vom Indikator X abhängt. Diese Position kann sowohl eine wissenschaftliche Hypothese sein als auch auf dem elementaren gesunden Menschenverstand beruhen. Nehmen Sie zum Beispiel Lebensmittelgeschäfte.

Bezeichnen mit:

X - Verkaufsfläche (sq. M.)

Y - Jahresumsatz (Mio. p.)

Je höher die Handelsfläche, desto höher ist natürlich der Jahresumsatz (wir gehen von einer linearen Beziehung aus).

Stellen Sie sich vor, wir haben Daten zu einigen n Filialen (Einzelhandelsfläche und Jahresumsatz) - unserem Datensatz und k Einzelhandelsflächen (X), für die wir den Jahresumsatz (Y) vorhersagen möchten - unsere Aufgabe.

Wir nehmen an, dass unser Wert von Y von X in der Form abhängt: Y = a + b * X.

Um unser Problem zu lösen, müssen wir die Koeffizienten a und b wählen.

Lassen Sie uns zunächst die Zufallswerte a und b festlegen. Danach müssen wir die Verlustfunktion und den Optimierungsalgorithmus bestimmen.

Dazu können wir die Root Mean Square Loss-Funktion ( MSELoss ) verwenden. Es wird nach folgender Formel berechnet:



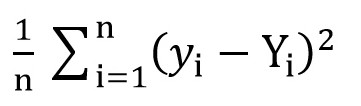
Wobei y [i] = a + b * x [i] nach a = rand () und b = rand () ist und Y [i] der korrekte Wert für x [i] ist.
Zu diesem Zeitpunkt haben wir die Standardabweichung (eine bestimmte Funktion von a und b). Und es ist offensichtlich, dass je kleiner der Wert dieser Funktion ist, desto genauer werden die Parameter a und b in Bezug auf diejenigen Parameter ausgewählt, die die genaue Beziehung zwischen der Fläche der Verkaufsfläche und dem Umsatz in diesem Raum beschreiben.

Jetzt können wir mit dem Gradientenabstieg beginnen (nur um die Verlustfunktion zu minimieren).

Gefälle Abstieg

Sein Wesen ist sehr einfach. Zum Beispiel haben wir eine Funktion:

y = x*x + 4 * x + 3 

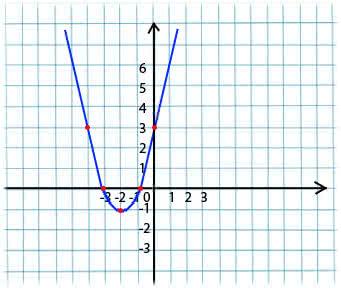
Wir nehmen einen beliebigen Wert x aus der Domäne der Funktion. Stellen Sie sich vor, dies ist der Punkt x1 = -4.

Als nächstes nehmen wir die Ableitung in Bezug auf x dieser Funktion am Punkt x1 (wenn die Funktion von mehreren Variablen abhängt (zum Beispiel a und b), müssen wir die partiellen Ableitungen für jede der Variablen nehmen). y '(x1) = -4 <0

Jetzt erhalten wir einen neuen Wert für x: x2 = x1 - lr * y '(x1). Mit dem Parameter lr (Lernrate) können Sie die Schrittgröße einstellen. So bekommen wir:

Wenn die partielle Ableitung an einem gegebenen Punkt x1 <0 ist (die Funktion nimmt ab), bewegen wir uns zum Punkt des lokalen Minimums. (x2 wird größer als x1 sein)

Wenn die partielle Ableitung an einem gegebenen Punkt x1> 0 ist (die Funktion nimmt zu), bewegen wir uns immer noch zum Punkt des lokalen Minimums. (x2 wird kleiner als x1 sein)

Indem wir diesen Algorithmus iterativ ausführen, nähern wir uns dem Minimum (erreichen es aber nicht).

In der Praxis sieht dies alles viel einfacher aus (ich nehme jedoch nicht an, zu sagen, welche Koeffizienten a und b für den obigen Fall mit Geschäften am besten geeignet sind, daher nehmen wir eine Abhängigkeit von der Form y = 1 + 2 * x, um den Datensatz zu generieren, und trainieren dann unser Modell weiter dieser Datensatz):
(Der Code ist hier geschrieben)

 import numpy as np #      np.random.seed(42) #  np-  1000     0..1 sz = 1000 x = np.random.rand(sz, 1) #   y = f(x)      y = 1 + 2 * x + 0.1 * np.random.randn(sz, 1) #    0  999 idx = np.arange(sz) #    np.random.shuffle(idx) train_idx = idx #     x_train, y_train = x[train_idx], y[train_idx] #        a = np.random.randn(1) b = np.random.randn(1) print(a,b) #   lr = 0.01 #   n_epochs = 10000 #   for epoch in range(n_epochs): #       a  b #     yhat = a + b * x_train # 1.   #      : error = (y_train - yhat) # 2.   (  ) #   a a_grad = -2 * error.mean() #   b b_grad = -2 * (x_train * error).mean() # 3.  ,     a = a - lr * a_grad b = b - lr * b_grad print(a,b) 

Nachdem Sie den Code kompiliert haben, können Sie sehen, dass die Anfangswerte von a und b weit von den erforderlichen 1 bzw. 2 entfernt waren und die Endwerte sehr nahe beieinander liegen.

Ich werde ein wenig klären, warum a_grad und b_grad so betrachtet werden.
F(a, b) = (y_train - yhat) ^ 2 = (1 + 2 * x_train – a + b * x_train) . Die partielle Ableitung von F in Bezug auf a ist -2 * (1 + 2 * x_train – a + b * x_train) = -2 * error . Die partielle Ableitung von F in Bezug auf b ist -2 * x_train * (1 + 2 * x_train – a + b * x_train) = -2 * x_train * error . Wir nehmen den Mittelwert (mean()) da error und x_train und y_train Arrays von Werten sind, a und b Skalare sind.

Im Artikel verwendete Materialien:

in Richtung Datascience.com/understanding-pytorch-with-an-example-a-step-by-step-tutorial-81fc5f8c4e8e
www.mathprofi.ru/metod_naimenshih_kvadratov.html