👎🏻 🥔 😋 Die Zahl, die der modernen Musik zugrunde liegt 📒 🙅🏼 🚿

Warum zwölf?

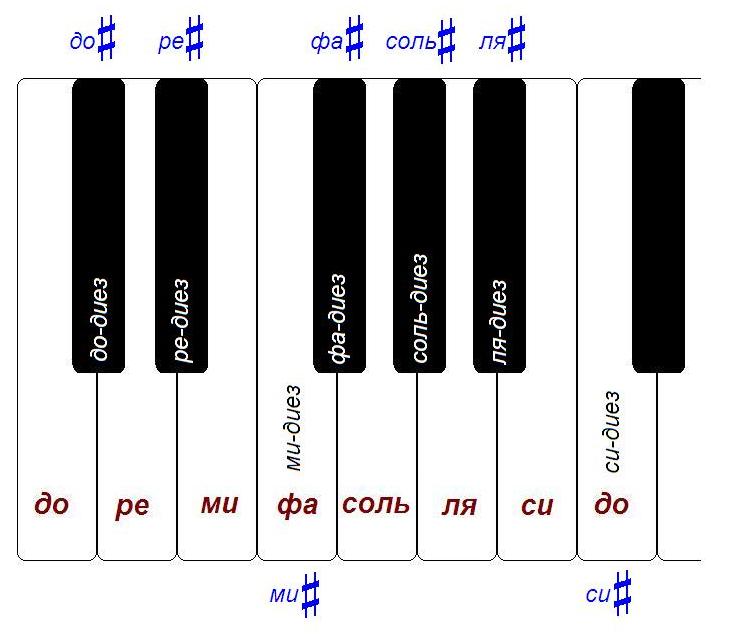
Wenn Sie auf die Tastatur schauen, werden Sie sehen, dass jede Oktave 12 Halbtöne enthält.
Beim Klavier bedeutet dies nur, dass zwischen beispielsweise „bis“ zur ersten Oktave und „bis“ zur zweiten Oktave 11 Tasten liegen. Zusammen mit einem der "do" (zum Beispiel bis zur zweiten Oktave) erhalten wir 12 Tasten: do #, re, re #, mi, fa, fa #, Salz, Salz #, la, la #, si, do.

Aber warum 12?

Vielleicht ist das nur ein Unfall? Unseren Vorfahren gefiel die Zahl 12, sie haben überall 12: 12 Monate, 12 Sternzeichen, 12 Stämme Israels, 12 Apostel ... und hier beschlossen sie, es 12 zu sein, und so wurde es befohlen. Oder gibt es noch ein objektives Gesetz, und diese Zahl ist nicht zufällig?

In diesem Artikel werde ich versuchen zu zeigen, dass dies kein Unfall ist. Ausreichend allgemeine Anforderungen, die für die moderne (westliche) Musik ganz natürlich sind und mathematisch notwendig sind, führen uns zur Zahl 12. Es ist interessant, dass der Grund, warum wir diesen Wert haben, die Eigenschaft einer anderen Zahl ist (siehe Ende des Artikels). Man kann sogar sagen, dass es im Herzen des modernen Klangs liegt.

Erklärung des Problems

Versuchen wir zunächst, die Aufgabe zu formalisieren.

Wir haben eine Referenzfrequenz $\ omega_0$ . Wir werden es Tonic nennen. Wir haben auch eine Oktave mit einer Frequenz $2 \ omega_0$ . Jetzt müssen wir verstehen, aus welchen Optionen für Zwischenfrequenzen $\ omega_0$ vorher $2 \ omega_0$ , so dass eine auf diesen Noten aufgebaute Melodie für unsere Ohren harmonisch klingt?

Ich befürchte, dass diese Formulierung, obwohl sie das Wesen der Frage widerspiegelt, aus mathematischer Sicht immer noch ziemlich vage ist, und eine solche Frage kann nicht eindeutig beantwortet werden, schon allein deshalb, weil das menschliche Gehör eine eher begrenzte Frequenzauflösung hat. Dies wird durch die Tatsache bestätigt, dass zu unterschiedlichen Zeiten unterschiedliche Systeme verwendet wurden, beispielsweise Pythagoras , saubere , gut temperierte , gleichmäßig temperierte Systeme. Und sie alle klangen und klangen, zumindest für bestimmte Werke, durchaus akzeptabel.

Was ist Harmonie?

Wir müssen einige zusätzliche Bedingungen auferlegen. Aber zuerst müssen wir eine wichtige Frage beantworten: Was nehmen wir als harmonischen Klang wahr?

Schauen wir uns zwei Geräusche an - mit Frequenzen $\ omega_1$ und $\ omega_2$ .

Nehmen Sie das Verhältnis dieser Frequenzen. Diese Beziehung kann als Produkt von Zahlen dargestellt werden $a_1 ^ {k_1} \ cdot a_2 ^ {k_2} \ cdot ... \ cdot a_l ^ {k_l}$ wo $inline$ Sind Primzahlen und $inline$ - Ganzzahlen, zum Beispiel kann dieses Verhältnis gleich sein $2 ^ {- 3} \ cdot3 \ cdot5$ . Und als diese Primzahlen ( $inline$ ) weniger, je harmonischer dieses Intervall für unser Ohr klingt (ich habe diese Aussage hier gefunden (siehe den zweiten Absatz) )

So ist beispielsweise der harmonischste Klang gemäß dieser Aussage eine Oktave (Frequenzänderung um das Zweifache). Und die nächsten harmonischen Intervalle sind die fünften (Frequenzänderung in $inline$ mal) und ein Quart (Frequenzänderung in $inline$ mal).

Aber nicht so einfach mit dieser Aussage. So ist zum Beispiel nicht sehr klar, wie sich der Abschluss auswirkt. Zum Beispiel, was ist harmonischer Multiplikation mit $inline$ oder 7? Ich weiß nicht, ob diese Frage untersucht wurde oder nicht, und ist es grundsätzlich möglich, eine Antwort darauf zu geben. Auch die Wahrnehmung von Harmonie ist eine eher subjektive Sache. Moderne Musik ist also voller Klänge, die 100 bis 200 Jahre lang als schreckliche Kakophonie wahrgenommen worden wären.

Die erste Bedingung. Tonic, Quart, Quint, Octave

Diese Unsicherheit ist für unsere kleine Forschung kein Problem. Tatsache ist, dass die einzige Schlussfolgerung, die ich aus dieser Aussage ziehen möchte, ist, dass es in unserem Fall auf jeden Fall mindestens die "harmonischsten" Intervalle geben sollte, nämlich eine Oktave, ein Quart und ein Fünftel. Das heißt, zusammen mit Tonic mit einer Frequenz $\ omega_0$ und Oktave mit einer Frequenz $2 \ omega_0$ Wir müssen auch eine fünfte und eine vierte mit Frequenzen haben ${3 \ over 2} \ omega_0$ , ${4 \ over 3} \ omega_0$ oder etwas sehr Nahes, das wir nicht von einem reinen fünften und vierten unterscheiden konnten.

Hinweis: Tatsächlich reichen nur Tonika, Quinten und Oktaven aus. Das Vorhandensein eines fünften gibt uns sofort einen Quart als Ergänzung zu einer Oktave, und aufgrund der zweiten Bedingung (Invarianz), die unten beschrieben wird, müssen wir auch einen Quart und ein Tonikum haben. Das heißt, die Notwendigkeit eines Quart ist eine Folge des Vorhandenseins eines Fünftels und des Erfordernisses der Invarianz.

Und das ist unsere erste Anforderung.

Die zweite Bedingung. Invarianz

Unsere zweite Anforderung ist die Invarianz. Und das ist eine wichtige Voraussetzung für moderne Musik. Diese Anforderung besteht darin, dass alle Harmonien in beliebigen Tasten gleich klingen sollten. Wenn wir über das moderne System sprechen, mit dem das Klavier gestimmt wird, bedeutet dies, dass das fünfte, bestehend aus sieben Halbtönen, gleich klingen sollte, unabhängig davon, aus welchem Klang es aufgebaut ist. Das heißt, das Frequenzverhältnis zwischen do und salt sollte das gleiche sein wie für do # - salt #, re - la, re # - la #, ... und gleich $inline$ . Und diese Invarianz sollte natürlich nicht nur für die fünfte, sondern auch für alle Intervalle gelten. Ein wichtiger Vorteil dieses Systems ist die Möglichkeit, das Spiel in jedem Intervall zu transponieren. Dies ist die Essenz eines einheitlichen Temperaments.

Ich muss sagen, dass dieses Erfordernis der Invarianz nicht so offensichtlich ist, und dieser Ansatz wurde erst vor relativ kurzer Zeit im 18. Jahrhundert angewendet. Die zuvor verwendeten Systeme (zum Beispiel Pythagoras und pure) besaßen keine solche Eigenschaft. Hören Sie sich zum Beispiel die Sonate für mikrotonales Klavier (Ben Johnston) an , die in einem sauberen System geschrieben wurde (Primzahl = 5). Es fühlt sich an, als wäre das Klavier nicht gestimmt. Der ganze Reichtum moderner Harmonien basiert genau auf dieser Invarianz. Zum Beispiel erschien Bachs "Wohltemperiertes Klavier" genau dank eines neuen Ansatzes zum Stimmen von Keyboards. Es war diese Invarianz, die es Bach ermöglichte, harmonische Sequenzen zu erzeugen, die vorher einfach unmöglich waren.

Jetzt haben wir also alle Daten, die für die Berechnung erforderlich sind.

Berechnung

Lassen Sie uns eine Skala von Tonika bis Oktaven erstellen, die beide Anforderungen erfüllt.
Nehmen wir an, dass wir in diesem Fall bekommen $inline$ Sounds (einschließlich einer Oktave). Das $inline$ und ist die gewünschte Anzahl. Das wollen wir zeigen $inline$ unter unseren Bedingungen sollte 12 sein.

Eine Konsequenz der zweiten Anforderung ist, dass das Intervall zwischen den Frequenzen benachbarter Töne gleich und gleich sein sollte $2 ^ {1 \ über N}$ .

Die erste Anforderung besagt nun, dass in unserer Zeile zwei Töne vorhanden sein sollten, die (mit guter Annäherung) Frequenzen entsprechen ${3 \ over 2} \ omega_0$ und ${4 \ over3} \ omega_0$ . Dies ist der fünfte und vierte. Angenommen, ein Quart ist $inline$ Ton in unserer Reihe und der fünfte - $inline$ oh. Wir bezeichnen $inline$ .

Es ist leicht zu erkennen, dass die Frequenzänderung zwischen dem vierten und fünften (Frequenzverhältnis) ist $inline$ .

Nach unserer zweiten Bedingung sollte dies aber auch gleich sein $2 ^ {n \ over N}$ .

Also haben wir die Formel bekommen:

$2 ^ {n \ over N} \ ca. 9/8$

Nach einfachen Transformationen erhalten wir die Grundformel:

$n \ ca. N (2 \ log_2 {3} - 3) = N \ cdot 0.170$

Es ist leicht zu erkennen, dass die Lösung (natürlich ungefähr) ist $inline$ wo $inline$ - natürlich jede Zahl (klein genug, da sich dennoch 0,170 von 1/6 unterscheidet).

Schauen wir uns einen Fall an $inline$ . In diesem Fall $inline$ , $inline$ . Das heißt, dies ist eine Variante des modernen Systems, nur ohne Halbtöne, nur mit Tönen (do, re, mi, fa #, salt #, la #, do). Wie Sie sehen, fielen in diesem Fall Quart (f) und Quint (Salz) nicht in diese Skala.

Das heißt, die einzige Option für uns kann sein

$inline$ wo $inline$ - jede natürliche Zahl ( $inline$ klein genug). Fall $inline$ entspricht nur unserem modernen System, das als einheitlich temperamentvolles System bezeichnet wird.

Aber warum nicht 24 oder mehr? Der Grund ist einfach - ich kann davon ausgehen, dass ein solcher Abschluss für unsere Wahrnehmung bereits übertrieben ist. Daher bleibt nur eine Nummer übrig: 12.

Wenn Sie mit dem gegebenen Gedankengang nicht zufrieden sind, finden Sie hier

strenger mathematischer Beweis

Herausforderung:

Finden Sie die minimale positive ganze Zahl N, bei der es eine positive ganze Zahl gibt $inline$ so dass $2 ^ {n \ over N}$ anders als $3 \ over2$ nicht mehr als $\ delta$ Cent .

Lösung:

Bezeichnen mit $Z_n = N \ cdot (log_2 {3} -1)$ . Dann mit $\ delta <{1200 \ über N}$ (was für die Reichweite dieser gilt $\ delta$ und $inline$ was wir betrachten werden) unsere Aufgabe ist es, das Minimum zu finden $inline$ bei denen

${1200 \ über N} \ cdot | Z_n - Runde (Z_n) | <\ delta$ ,

wo $inline$ - Funktionsrundung auf die nächste ganze Zahl.

Wir werden dieses Problem numerisch lösen.

Bild

Jetzt ist es Zeit zu entscheiden $\ delta$ .

Welchen Betrag (in Cent) der Diskrepanz zwischen dem reinen fünften und „unserem fünften“ halten wir für akzeptabel? Viele Leute hören zum Beispiel, dass das große / kleine Drittel im gleichmäßig temperierten System "fälscht". Dies sind jedoch nur etwa 15 Cent im Verhältnis zu reinen Intervallen. Daher sollte unser Bedarf besser als 15 Cent sein. Einige Quellen sagen, dass Musiker bei bestimmten Frequenzen bis zu 5 - 6 Cent unterscheiden. Deshalb klug zu nehmen $\ delta = 5$ .

Dann zeigt die Tabelle deutlich, dass die kleinste $inline$ . Die folgenden sind zufriedenstellend $inline$ .

Hinweis:
Nächste Iteration für jede $inline$ Sie müssen auch den Ton und andere Intervalle überprüfen. Im Fall von $inline$ Zum Beispiel werden Drittel vollständig "falsch": mehr als 30 Cent (für ein großes Drittel).

Unsere Antwort lautet also: $inline$ . Welches musste beweisen.

Übrigens ist klar, dass sich unsere Antwort nicht ändern wird, wenn wir stattdessen $\ delta = 5$ Nehmen Sie zum Beispiel 10 oder sogar 15.

Fazit Basisnummer

Überraschenderweise stellt sich heraus, dass die Zahl, die dem modernen Musiksystem und der zeitgenössischen (europäischen) Musik zugrunde liegt, ist $\ log_2 {3}$ , nämlich dass mit guter Genauigkeit (0,1%) die folgende Gleichheit gilt:

$\ log_2 {3} \ ca. 19/12$

Antworten auf Kommentare und Kritik in den Kommentaren

Zunächst einmal vielen Dank für die interessanten Kommentare!
Hier sind meine Antworten auf die wichtigsten (meiner Meinung nach) Kommentare und Kritikpunkte.

Kritik 1. Ei oder Huhn

Druu: Schauen Sie, 12 Klänge in einer Oktave entsprachen im Allgemeinen einem einheitlichen Temperament. Sie können also 12 Klänge nicht mit Hilfe des Temperaments rechtfertigen. Dies ist einfach falsch.

lair: Dies ist genau die Ringlogik, von der ich spreche: Wenn Sie Musik wählen, die auf einem bestimmten System basiert, ist es offensichtlich, dass in seinem Kontext ein anderes System unmöglich ist.

Zu diesen und ähnlichen Bemerkungen möchte ich zwei Gegenargumente anführen:

1) wenn mit ausreichender Genauigkeit die Gleichheit $log_2 {3} = 19/12$ dann wäre es unmöglich, ein einheitliches Temperamentsystem in ein reines System zu "ziehen", das aus 12 Klängen besteht. Je stärker $log_2 {3}$ anders als $inline$ Je falscher unser fünfter klingen würde. Wenn diese Zahl (stark) unterschiedlich wäre, gäbe es keine einheitlich temperamentvolle Herangehensweise an reine Intervalle, und infolgedessen gäbe es keine moderne Musik, oder sagen wir, es wäre anders. Daher ist die Schlussfolgerung, dass die Eigenschaften der Zahl ziemlich logisch sind $log_2 {3}$ sind das Fundament der modernen Musik.

2) Das zweite Gegenargument ist logisch nicht zu rechtfertigen und nur eine Annahme, aber es scheint mir, dass all diese Überlegungen Beachtung verdienen. Versuchen wir, die Frage zu beantworten, warum überhaupt ein einheitlich temperiertes System erforderlich ist. Die Kommentare wurden bereits teilweise beantwortet. Musik zu dieser Zeit (der Zeit der Schaffung eines einheitlichen Temperamentsystems) verwendete bereits Modulationen und Polyphonie, die im Großen und Ganzen bereits ein einheitliches Temperament erforderten. Das Problem des "falschen" Klangs wurde durch die Tatsache gelöst, dass die Musiker den Klang während der Aufführung leicht "anpassten". Es war einfach für Streicher (zumindest ohne Bund), Bläser und Gesang (richtig, wenn ich falsch liege - ich habe diese Schlussfolgerung aus Ihren Kommentaren gezogen). Zum Beispiel für die Geige - dies ist nur eine geringfügige Änderung der Position der Finger. Aber sobald Ihnen eine solche Gelegenheit genommen wurde (Cembalo), begann sofort alles schlecht zu klingen. Es sieht also so aus, als wären diese 12 Noten nicht nur so erschienen, sondern als natürliche Entwicklung der Musik hin zu dieser Möglichkeit freier Modulationen und reicher Polyphonie, und dies ist wiederum eine Folge der Invarianz. Es war eine natürliche Entwicklung der Musik. Das heißt, ich möchte sagen, wenn eine mathematische Invarianz nicht für 12 Töne möglich wäre, sondern zum Beispiel für 10, dann hätten wir (noch vor dem einheitlichen Temperament) in unserer Skala 10 Töne (in diesem Fall spreche ich über den Weg Entwicklung der europäischen Musik). Und dann würden 10 Geräusche von einheitlichem Temperament auf unser reines System gezogen.

Kritik 2. Die Einzigartigkeit der Zwölf

Es gab viel Kritik an der Behauptung, dass 12 die einzig vernünftige Zahl ist.

Erstens habe ich, als ich die Aggressivität dieser Aussage und das Prinzip der Unmöglichkeit einer strengen Rechtfertigung verstand, möglicherweise den Grad der Kategorisierung einiger der in dem Artikel enthaltenen Behauptungen verringert. Und doch ...

In diesem Fall haben wir zwei Kritikpunkte.

1) Warum halte ich 19, 24 oder 29 (usw.) für inakzeptabel?

Nein, das glaube ich nicht. Für verschiedene Instrumente gibt es Techniken zur Verwendung von Klängen außerhalb der Skala, z. B. Glissando und Vibrato. Diese Techniken verleihen dem Klang Schönheit und Natürlichkeit. Daher verwenden wir auch bei 12 Noten noch Hilfstöne. Wenn wir über Umgebung sprechen, über ungewöhnlichen Klang, über die Anreicherung des Klangs ... dann ist dies durchaus gerechtfertigt, aber wenn wir über Grundtöne sprechen, dann habe ich Zweifel. Musik wird nicht nur für die Elite geschaffen, sondern auch für gewöhnliche Menschen, und für sie ist ein solcher Abschluss (IMHO) nicht erforderlich.

Das zweite Argument, und es wurde in den Kommentaren gegeben, ist in der Tat die Komplexität der Schaffung von Instrumenten und der Aufführung im großen Maßstab, obwohl wir ein großartiges Beispiel für ein solches Instrument haben - die Sitar. Versuchen Sie jedoch, eine Oktave (mit einer Hand) auf dem Klavier zu spielen, wenn Sie eine Skala von 24 Klängen haben.

2) Aber was ist mit Pentatonik?

In allen östlichen Ländern, in denen ich war, hörte ich aus irgendeinem Grund sehr selten nationale Musik auf pentatonischer Ebene. Und alle Musiker aus dem Osten, die ich gehört habe (und ich liebe einige), haben auch ziemlich europäische Musik gespielt. Hier ein interessantes Zitat : "Akademische Komponisten verwenden seit dem 19. Jahrhundert Pentatonik als Spezialfarbe, um der Musik einen archaischen Geschmack zu verleihen." Das Aroma von archaischen ...
In meiner Wahrnehmung ist diese Musik dennoch nicht modern, aber ich möchte diese Position nicht verteidigen, daher verwende ich an einigen Stellen im Artikel den Begriff "moderne europäische Musik". Es ist klar, dass diese Musik (auf der pentatonischen Skala aufgebaut) sich nach anderen Gesetzen entwickelte und nicht die Nachfrage nach reicher Polyphonie und häufiger und einfacher Modulation erreichte, die in der europäischen Musik auftrat. Daher geht es in diesem Artikel offensichtlich nicht um Pentatonik.

Kritik 3. Zeitgenössische Musik

Wie nenne ich moderne Musik?

Obwohl dies wie eine Tautologie klingt, meine ich mit moderner Musik Musik, die Invarianz erfordert, was bei Instrumenten mit einem festen System (z. B. Cembalo, Klavier) zur Notwendigkeit eines gleichmäßig gemäßigten Systems (oder etwas Nahem) führt. Bei anderen Instrumenten, zum Beispiel Saiten ohne Bund, sieht alles etwas komplizierter aus, da in der Realität ein größerer Satz (als 12) von Klängen verwendet werden kann. Wenn wir jedoch über das Erfordernis der Invarianz sprechen, meinen wir, dass diese Geräusche sehr nahe (in der Frequenz) an unseren 12 liegen sollten.

Diese Definition umfasst fast alle Klaviermusik, europäische Klassik, Jazz, Rockmusik, Pop und alle Derivate davon. Ich bin sicher, dass es Ausnahmen gibt, aber meiner Meinung nach sind dies die Ausnahmen. Ich sehe keinen Grund, darüber zu streiten, weil Jeder kann etwas in dieses Konzept investieren.

Kritik 4. Berechnung

Fehler in den Berechnungen.

Ich denke, diese Frage ist entfernt. Ich muss jedoch zugeben, dass ich während der Diskussion mehrere fehlerhafte Aussagen zu Nebenthemen gemacht habe, die die Hauptschlussfolgerung des Artikels nicht beeinflusst haben.

PS Behandeln Sie diesen Artikel nicht (und stellen Sie die entsprechenden Anforderungen) als akademische Arbeit. :) Dies ist kein Artikel zur Musiktheorie. Darüber hinaus ist dies kein Artikel zur Musikgeschichte. In diesen Bereichen halte ich mein Wissen in keiner Weise für zumindest irgendwie bedeutsam und gebe zu, dass es möglicherweise Ungenauigkeiten gibt, obwohl ich versucht habe, sie zu vermeiden. Hier wird ein einfaches mathematisches Problem formuliert (von einem schulischen Komplexitätsniveau), dessen Lösung, wie es mir schien, eine interessante Interpretation hat. Mit dem ich geteilt habe.

Die Zahl, die der modernen Musik zugrunde liegt