
Ich bin sicher, dass viele der Leser manchmal im Klassenzimmer nutzlosen Unsinn betreiben, anstatt dem Lehrer zuzuhören. Ich habe genau das getan, und eine Möglichkeit, die Zeit totzuschlagen, bestand darin, auf Papier zu spielen. Das Vorschau-Spiel (dessen Name mir noch unbekannt ist) erschien mir besonders interessant, aber es gibt zwei Gründe: Es erfordert keine zweite Person und kann abgeschlossen werden! Es war zwar äußerst selten, dies zu tun. Lange habe ich mich gefragt, wie einfach sich die Lösung herausstellen könnte, und jetzt, nach vielen Jahren, wird es nicht schwierig sein, sie programmgesteuert zu finden.
Die Regeln
Zunächst lohnt es sich, die Regeln zu beschreiben. Das Spiel beginnt mit folgendem Feld:
123456789
111213141
516171819
Hier werden alle Zahlen von 1 bis 19 Zeichen für Zeichen aufgezeichnet, mit Ausnahme von 10. Die Zahlen befinden sich Zeile für Zeile von links nach rechts. Die Regeln sind recht einfach: Bei jedem Schritt müssen Sie zwei Zahlen streichen, die den folgenden Kriterien entsprechen:
- Die Zahlen müssen entweder gleich sein oder insgesamt 10 ergeben (1 und 1, 3 und 7, 8 und 2 usw.).
- Sie müssen entweder übereinander stehen oder in Reihe angeordnet sein. In diesem Fall werden bereits durchgestrichene Zahlen ignoriert.
Eine der Optionen für die ersten Züge ist unten dargestellt:
1 23456789
1 11213141
5161718 19
#2345678 9
# 1 1213141
5161718##
#2345678#
##1213141
5161718##
In dem Moment, in dem es keine Züge mehr gibt, werden alle nicht markierten Zahlen am Ende hinzugefügt. Das Spiel endet, wenn das gesamte Feld durchgestrichen ist.
#2345678#
##1213141
51 6 171 8 ##
23 4 567 8 12
131415161
718
#2345678#
##1213 1 41
5 1 # 1 71###
23#567#12
131415 1 61
718
#2345678#
##1213#41
5###71###
2 3 #567#12
1 3 1415#61
718
...
Die Anzahl der verfügbaren Züge nimmt rapide zu, das Spiel beginnt sich stark zu verzweigen. Oft wird die Tabelle so lang, dass sie zur nächsten Seite in einem Notizbuch überläuft. Es ist einfacher, eine neue Charge zu starten. Manchmal fuhr ich aus Ausdauer fort, aber am Ende gab ich auf.
Dies wirft die vernünftige Frage auf: Wie schnell kannst du dieses Spiel beenden? In der Kindheit war es möglich, eine Lösung in einer Spalte auf einem Notizbuchblatt zu finden - das sind ungefähr 40 Zeilen oder 360 Zeichen.
Ich weiß nicht, wie ich das Spiel garantiert abschließen kann. Es ist völlig unklar, wie man eine Strategie wählt. Sie können versuchen, es selbst zu spielen, wenn Sie es nicht haben.
Lösung
Wie werden Lösungen für solche Probleme gesucht? Ich weiß es nicht genau, aber ich habe die übliche Büste gewählt.
Wir brauchen eine Warteschlange, die zunächst nur aus einer einzigen Erstkonfiguration besteht. Bei jedem Schritt nehmen wir die folgende Konfiguration aus der Warteschlange, sehen uns alle verfügbaren Züge an und fügen sie entweder alle am Ende der Warteschlange hinzu oder erklären uns selbst zum Gewinner, wenn es keine solchen Züge gibt.
123456789 #23456789 12345678# 123456789 123456789 123456789 123456789 ...
111213141 #11213141 #11213141 ##1213141 1##213141 11#213141 11121314# ...
516171819 516171819 516171819 516171819 516171819 516#71819 51617181# ...
Wenn Sie sich nicht mit der ersten verfügbaren Lösung befassen, erzeugt dieser Algorithmus alle möglichen Lösungen (bei unendlich viel RAM).
In der Praxis hilft ein derart naiver Ansatz überhaupt nicht, zumindest aufgrund der ständig auftretenden Duplikate in der Warteschlange. Daher sind einige Optimierungen erforderlich, die ich nun erläutern werde:
- Konfigurationen müssen natürlich zwischengespeichert werden, um sie nicht erneut in die Warteschlange zu stellen. Dies erhöht die Speichernutzung erheblich, hilft jedoch nicht, in angemessener Zeit eine Lösung zu finden. Darüber hinaus stellt sich die Frage nach dem Vergleich von Konfigurationen stark. Da zwei Gewinnkonfigurationen derselben Größe immer nur aus durchgestrichenen Zahlen bestehen, ist ein zusätzlicher Weg erforderlich, um sie zu unterscheiden, da sonst nicht alle Lösungen gefunden werden.
- Um die Suche sinnvoll und schnell zu gestalten, ist es besser, eine Prioritätswarteschlange zu verwenden. Je weniger Zahlen auf dem Feld (einschließlich durchgestrichen), desto früher sollte eine solche Konfiguration in Betracht gezogen werden.
- Wenn Sie mehr als eine Lösung benötigen, aber viele, ist es besser, die maximale Anzahl von Zahlen auf dem Feld zu begrenzen. Bei der Suche werden Lösungen viel früher ausgegeben.
Die Antwort
Wenn alles korrekt ist, stellt sich heraus, dass die Mindestlösung nur aus 68 Zeichen oder 8 Zeilen besteht!
Ich werde es in Form von GIF-Animation bringen. Einige Züge wurden zu einem zusammengeklebt, um die Anzahl der Frames zu verringern:
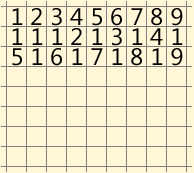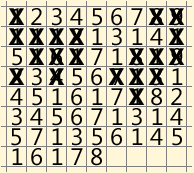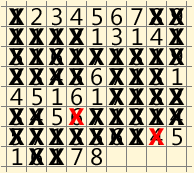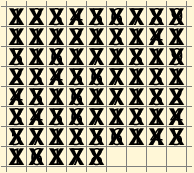
Ich bin ehrlich, ich war beeindruckt, wie kurz diese Entscheidung ist. Aber vielleicht werden dieses Glück und andere Entscheidungen nicht bald getroffen und werden sehr lange dauern?
Nein, Entscheidungen sind überhaupt nicht selten. Schnelle Antworten finden Sie in den Längen 72, 74 und 76. Und 4 grundlegend unterschiedliche Lösungen mit einer Länge von 80. Im Allgemeinen habe ich 30 Lösungen mit einer Länge von bis zu 90 (einschließlich) gefunden. Wenn ich die Grenze auf 100 erhöhe, gibt es 170 Lösungen. aber sie zu suchen wird teurer.
Unter dem Spoiler wird die optimale Lösung ausführlich beschrieben:
Versteckter Text 123456789 111213141 516171819 123456789 111213141 5161718## 123456789 1##213141 5161718## 12345678# 1##21314# 5161718## #2345678# ###21314# 5161718## #234567## ####1314# 5161718## #234567## ####1314# 5161718## 234567131 45161718 #234567## ####1314# 51#1718## 23#567131 45161718 #234567## ####1314# 51#171### #3#567131 45161718 #234567## ####1314# 51#171### #3#567#31 451617#8 #234567## ####1314# 51#171### #3#56###1 451617#8 #234567## ####1314# 5###71### #3#56###1 451617#8 #234567## ####1314# 5###71### #3#56###1 451617#82 345671314 571356145 16178 #234567## ####1314# 5###71### #3#56###1 451617#82 345671314 57#356145 16#78 #234567## ####1314# 5###71### #3#56###1 451617#82 345671314 5###56145 16#78 #234567## ####1314# 5###71### #3#56###1 451617#82 345671314 #####6145 16#78 #234567## ####1314# 5###71### #3#56###1 451617#82 34567131# ######145 16#78 #234567## ####1314# 5###71### #3#56###1 451617#82 3456713## #######45 16#78 #234567## ####1314# 5###71### #3#56###1 451617#82 3#56713## #######45 1##78 #234567## ####1314# 5###71### #3#56###1 451617### 3#56713## #######45 1##78 #234567## ####1314# 5###71### #3#56###1 45161#### ##56713## #######45 1##78 #234567## ####1314# 5###7#### #3#56###1 45161#### ##567#3## #######45 1##78 #234567## ####1314# 5######## ###56###1 45161#### ##567#3## #######45 1##78 #234567## ####1314# ######### ####6###1 45161#### ##567#3## #######45 1##78 #234567## ####1314# ######### ####6###1 45161#### ##56##### #######45 1##78 #234567## ####1314# ######### ####6###1 45161#### ##5###### ########5 1##78 #234567## ####1314# ######### ####6###1 45161#### ######### ######### 1##78 #234567## ####131## ######### ########1 45161#### ######### ######### 1##78 #234567## ####13### ######### ######### 45161#### ######### ######### 1##78 #234567## #####3### ######### ######### 4516##### ######### ######### 1##78 #23456### ######### ######### ######### 4516##### ######### ######### 1##78 #2345#### ######### ######### ######### #516##### ######### ######### 1##78 #234##### ######### ######### ######### ##16##### ######### ######### 1##78 #23###### ######### ######### ######### ##1###### ######### ######### 1##78 #23###### ######### ######### ######### ######### ######### ######### ###78 #2####### ######### ######### ######### ######### ######### ######### ####8 ######### ######### ######### ######### ######### ######### ######### #####
Mein Java-Lösungscode kann unter diesem Link angezeigt werden, aber ich warne Sie, dass es schrecklich ist, weil ursprünglich nicht zur Veröffentlichung geschrieben. In der aktuellen Form werden alle Lösungen mit bis zu 70 Zeichen gefunden (dh nur eine Lösung). Dies lässt sich leicht beheben, indem Sie mit den Bedingungen im Code herumspielen.
Vielen Dank für Ihre Aufmerksamkeit!