Im Jahr 2000 schlug
Angelo Farina , Professor an der Universität von Parma, eine
originelle Methode zur gleichzeitigen Messung der Impulsantwort und der nichtlinearen Verzerrung unter Verwendung eines harmonischen Signals mit exponentiell wechselnder Frequenz vor (im Folgenden: ESS - Exponential Sinus Sweep).
Um diese Eigenschaften zu erhalten, ist es erforderlich, die Wirkung des ESS-Signals auf das getestete Gerät aufzuzeichnen und die gegenseitige Korrelationsfunktion des aufgezeichneten Signals mit dem ursprünglichen ESS-Signal zu ermitteln, das jedoch in der Amplitude moduliert ist (weitere Einzelheiten siehe A. Farins Veröffentlichungen).
Das Ergebnis ist eine Reihe von Impulseigenschaften (IH), von denen die letzte eine lineare Impulsantwort des Geräts ist. Dem geht die Impulsantwort der quadratischen Nichtlinearität des Geräts voraus, bevor es die Impulsantwort der kubischen Nichtlinearität usw. ist. In der Praxis ist es möglich, Nichtlinearitäten von bis zu 20 Ordnungen zu fixieren.
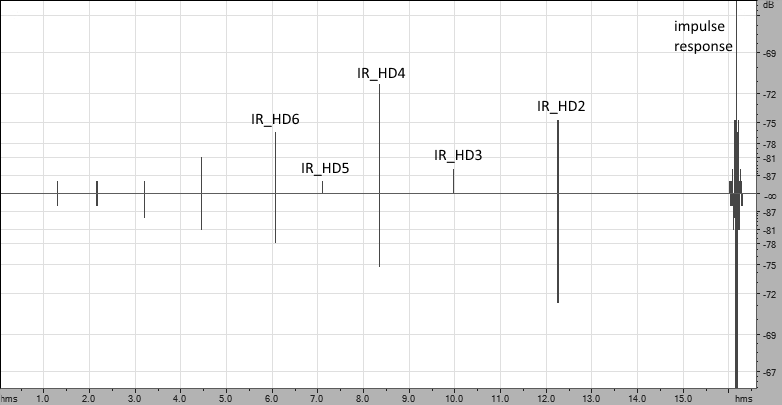
Dieses Merkmal (Trennung von Nichtlinearitätsprodukten von einer linearen Impulsantwort) ist ein einzigartiger Vorteil der ESS-Methode im Vergleich zu anderen Methoden. Die ESS-Methode hat weitere Vorteile:
- Erhöhte Beständigkeit gegen zufälliges Rauschen. Dies liegt daran, dass das harmonische Signal in jedem Zeitintervall eine sehr enge Frequenzspanne „abtastet“, wodurch der Pegel des zufälligen Rauschens in der resultierenden Impulsantwort verringert wird. Je länger das ESS-Signal ist, desto deutlicher wird der Effekt der Rauschunterdrückung.
- Benutzerfreundlichkeit. Der gesamte Decodierungsvorgang besteht aus mehreren FFT-Berechnungen.
- Möglichkeit zur Automatisierung des Messprozesses.
Der Ort der Verzerrungseigenschaften relativ zur linearen Impulsantwort kann durch die folgende Regel ermittelt werden: Wenn die Frequenz des ESS-Signals mit einer Geschwindigkeit von 1 Oktave pro Sekunde ansteigt, befindet sich die Nichtlinearitätscharakteristik zweiter Ordnung 1 Sekunde vor der linearen Impulsantwort; Die Nichtlinearitätskennlinie 4. Ordnung befindet sich 1 Sekunde vor der Kennlinie 2. Ordnung usw.
Trotz der offensichtlichen Vorteile hat die ESS-Methode ihre eigenen Anwendungsgrenzen. Der Autor der Methode selbst listet die folgenden Einschränkungen auf:
- Die resultierende Impulsantwort sowie ihr Frequenzgang weisen merkliche Ungleichmäßigkeiten auf ("Klingeln").
- Das Verfahren reagiert empfindlich auf die Instabilität der Zeitachse.
Um die Ungleichmäßigkeit des Frequenzgangs und die Impulsantwort zu verringern, schlägt A. Farina vor, den Beginn des ESS-Signals in der Amplitude (Einblenden) zu modulieren und verschiedene Filtertechniken anzuwenden.
Eine andere Enthusiastin, Katja Vetter, entdeckte in
seiner Forschung ein weiteres Problem, das damit zusammenhängt, dass nicht jede Oktave des Signals in der Nullphase beginnt. Dies führt zu einem Fehler bei der Messung von Harmonischen. Als Lösung schlug der Autor einen neuen Ansatz zur Bildung eines ESS-Signals vor: Jede Oktave sollte mit einer Nullphase beginnen.
Praktische Beispiele für die Anwendung der ESS-Methode.
Durch Auswahl und Modellierung in MATLAB wurde ein ESS-Signal mit einer Dauer von 43 Sekunden, einem Bereich von 11 Oktaven (11,7-24000 Hz) mit Amplitudenmodulation der Signalflanken erzeugt. Dies ermöglichte es, eine Frequenzgangungleichmäßigkeit <0,2dB an den Rändern des Messbereichs (22 und 23000 Hz) und einen relativen Fehlerpegel <-140 dB zu erhalten.
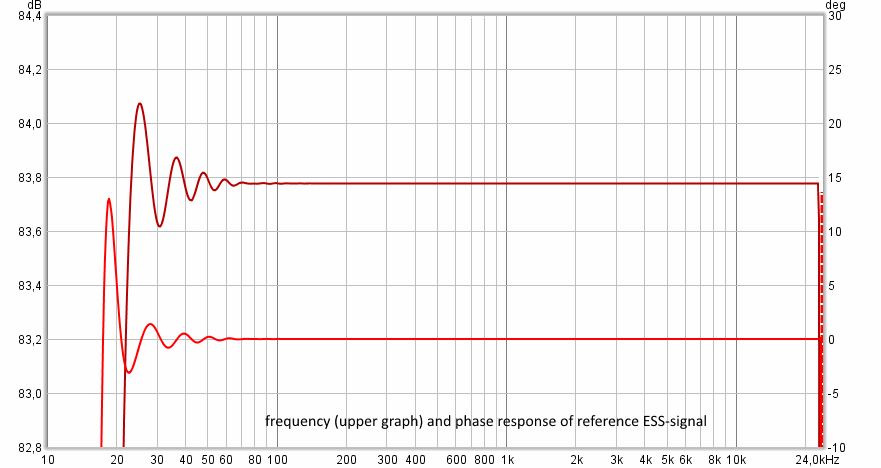
Messung der Eigenschaften von Equalizerzellen (Frequenzkorrektor).
Die ESS-Methode erwies sich als sehr nützlich beim Aufbau eines Equalizers, der an Operationsverstärkern montiert ist. Das Schema zeigte Instabilität, deren Ursache schwer zu analysieren war. Mit der ESS-Methode konnte festgestellt werden, dass das Gerät im Frequenzbereich des Equalizers vermehrt nichtlineare Verzerrungen aufwies.
Messung der Eigenschaften einer Computer-Audiokarte.
In diesem Beispiel wurde der Ausgang der Audiokarte mit dem Eingang verbunden und der Durchgangsfrequenzgang des Geräts gemessen. Wie Sie sehen können, ist eine gewisse Unebenheit (im Bereich von 20 bis 60 Hz) mit dem Fehler der ESS-Methode selbst verbunden. Der Rest des Beitrags zur Unebenheit bezieht sich auf die Audiokarte.
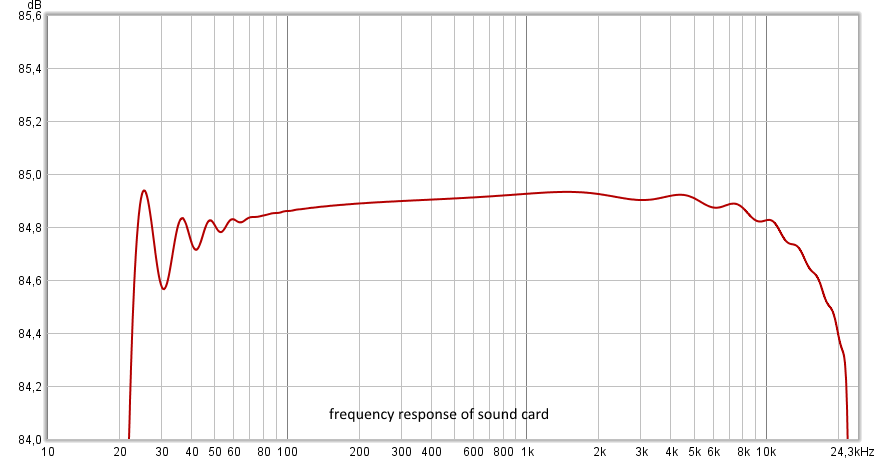
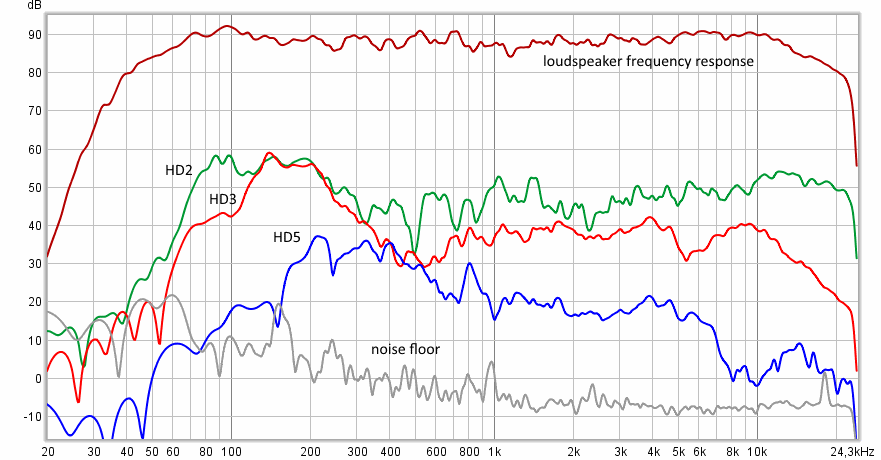
Akustische Messung des Lautsprechers
Dieses Beispiel zeigt Messungen des Frequenzgangs von Studiomonitoren im Nahfeld. In diesem Fall betrug das Signal-Rausch-Verhältnis 90 dB, während die Messungen in einem Studioraum bei einem moderaten Schalldruckpegel (nicht mehr als 90 dB Schalldruck) durchgeführt wurden.
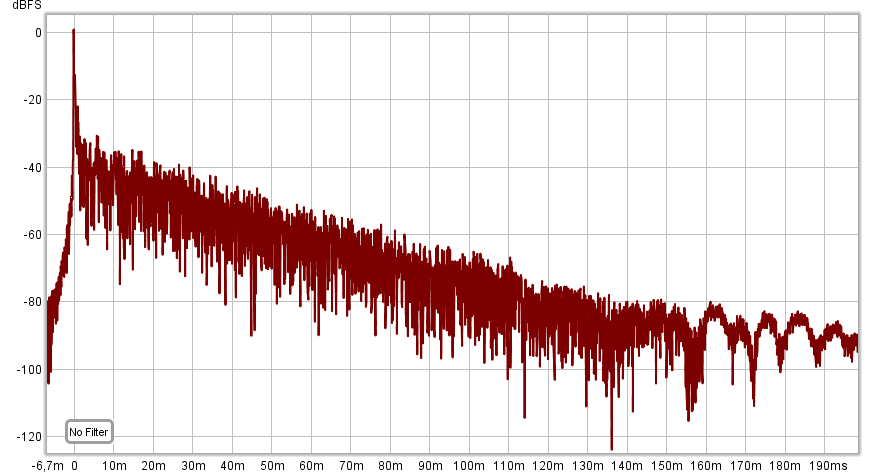Die Hüllkurve der gemessenen Impulsantwort des Studiomonitors (es ist ersichtlich, dass der dynamische Messbereich 90 dB betrug).Messung der akustischen Eigenschaften des Raumes
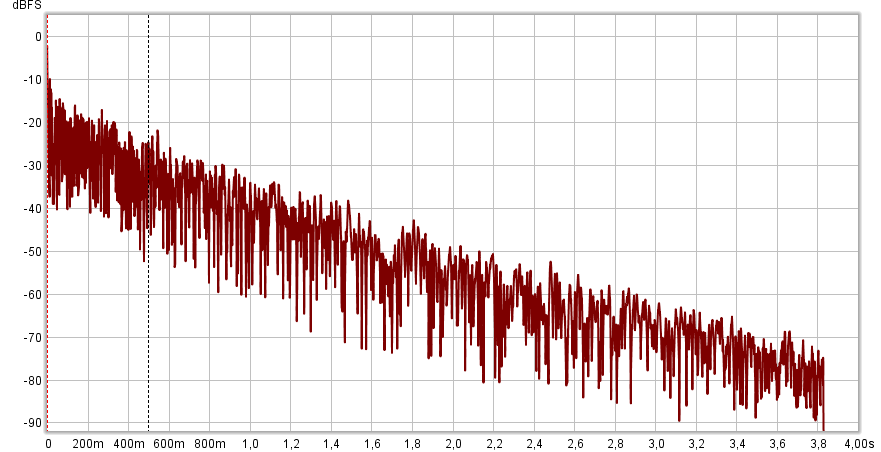
Dieses Beispiel zeigt die Hüllkurve der Impulsantwort eines Raums. Die Nachhallzeit betrug 3,8 Sekunden. Wie Sie sehen können, nimmt die Energie gleichmäßig und ohne Platzen bis zu den niedrigsten Werten ab.
Das von A. Farin vorgeschlagene Verfahren ermöglicht hochpräzise Messungen elektronischer und elektroakustischer Geräte sowie der akustischen Eigenschaften der Räumlichkeiten. Es ist bekannt, dass diese Methode erfolgreich in akustischen Messprogrammen wie
CLIO und
REW eingesetzt wird .
Nützliche Links:
- Gleichzeitige Messung von Impulsantwort und Verzerrung mit einer Swept-Sinus-Technik
- Fortschritte bei der Messung der Impulsantwort durch Sinus-Sweeps
- Messung der Impulsantwort mit Sinus-Sweeps und Amplitudenmodulationsschemata
- Optimierung des ESS-Signals (Exponential Sinus Sweep) für In-situ-Messungen an Lärmschutzwänden