Mathe Liebe

Basierend auf einem Artikel von Julien Clinton Sprott. Dynamische Modelle der Liebe. Nichtlineare Dynamik Psychologie und Biowissenschaften, August 2004.

Ich glaubte an Harmonie in der Algebra ...
Die Theorie meines Freundes ist trocken, aber der Baum des Lebens ist immer grün ...

Wer hat gerade nicht über dieses "Problem" gekämpft .... Es wurde in antiken griechischen Tragödien zerlegt, der große Shakespeare erzählte uns die Geschichte von Romeo und Julia, Andrzej Wajda zerlegte es von beiden Seiten in der Anatomie der Liebe. Aber die Menschen sind der Wahrheit nie auf den Grund gegangen, bis Wissenschaftler die Entscheidung getroffen haben. Zwar scheint Psychologen nicht alles überzeugend zu sein. Sie selbst beginnen manchmal sogar nach ihrer eigenen Scheidung, die Geschichte ihrer verstorbenen Liebe zu analysieren. Schreiben Sie Bücher, die manchmal wie heiße Kuchen aussehen. Sie werden von Experten geschrieben! Was kann ich sagen Fast nichts Persönliches - nur Geschäftliches ...

Und schließlich liebten sich keine Dichter mit Schriftstellern und Psychologen am Hals. Mathematik ist die Königin der Wissenschaften. Kann sie ein ewiges Problem bewältigen? Bücher werden zum Beispiel von John Gotman, "The Mathematics of Marriage" und anderen Autoren veröffentlicht. Mathematiker betrachten die Entwicklung romantischer Beziehungen als einen dynamischen Prozess ...

Und alles beginnt wie erwartet mit Definitionen. Wie kann man Liebe qualitativ und quantitativ identifizieren? Forscher klassifizieren das Problem nach Typ: Liebesbeziehung, Leidenschaft, Treue. Darüber hinaus hat jede Art eine komplexe Reihe von Gefühlen. Aber neben der Liebe zu einem anderen Menschen gibt es auch Liebe zu sich selbst, zum Leben, zur Menschheit ...

Gleichzeitig kann das Gegenteil von Liebe - im mathematischen Modell - nicht gehasst werden, da beide Gefühle gleichzeitig koexistieren können. Zum Beispiel mag jemand einige Manifestationen eines Partners, andere mögen böse sein. Es ist daher unrealistisch anzunehmen, dass die Liebe eines Individuums nur von seinen eigenen Gefühlen beeinflusst wird und die Gefühle des anderen Partners nicht von anderen Einflüssen abhängen und dass die Parameter, die die Interaktion zweier Menschen charakterisieren, unverändert bleiben und somit die Möglichkeit des Lernens und der Anpassung ausschließen.

Die Komplexität selbst in einem minimal eingeschränkten Modell nimmt dramatisch zu, wenn drei oder mehr Variablen in die Gleichungen der Nichtlinearität und / oder eingeführt werden.

* Hinweis: Übersetzer. Meiner Meinung nach können solche Studien auch die Mathematik selbst wiederbeleben und die Aufmerksamkeit der Öffentlichkeit auf sich ziehen, die normalerweise von dieser abstrakten Wissenschaft entfremdet ist.

Einfaches lineares Modell

Die Liebesgeschichte von Romeo und Julia in der Zeit (t) kann mit den Funktionen * R (t) - Romeos Liebe zu Julia und J (t) - Julias Liebe zu Romeo dargestellt werden.

Dann wird ein einfaches lineares Modell ihrer Beziehung durch die Gleichungen (1) ausgedrückt.



a und b - Parameter des romantischen Stils von Romeo
c und d - Optionen für den Julia-Stil
a - charakterisiert, wie Romeo in seine eigenen Gefühle eingehüllt ist
b - wie sehr Romeo von Julias Gefühlen umarmt wird

In einem der Artikel (Gottman et al., 2002) wird der Begriff "Verhaltensträgheit" für den ersten und die "Einflussfunktion" für den zweiten Parameter verwendet. Obwohl bei a = 0, wird die Trägheit am größten. Das dynamische Modell ist unter solchen Bedingungen zweidimensional und durch die Anfangsbedingungen und vier Parameter steuerbar, die positiv oder negativ sein können.

Ein einfaches lineares Modell wurde von Rinaldi, 1998a, vorgeschlagen. Gleichzeitig wird jedem Derivat ein freier Begriff hinzugefügt, um die Attraktivität (oder Antipathie mit einem negativen Wert) zu berücksichtigen, die jeder der Partner dem anderen zeigt, wenn keine anderen Gefühle vorliegen. Ein solches Modell ist realistischer, weil es Gefühle aus einem Zustand der Gleichgültigkeit wachsen lässt und ein Gleichgewicht bietet, das nicht durch völlige Apathie gekennzeichnet ist. All dies wird auf diese Weise nur durch Eingabe von zwei zusätzlichen Parametern beschrieben. Während der Zustand des nicht-apathischen Gleichgewichts für die betreffenden Personen sehr wichtig sein kann, ändert dies die Dynamik nur durch Bewegen des Zustandsraums RJ.

Romantische Stile

Romeo kann abhängig von den Zeichen a und b einen von vier romantischen Stilen zeigen, wobei der Autor des Werkes (Strogatz, 1994) und seine Schüler die Notation angeben:

1. Leidenschaftliches Verlangen: a> 0, b> 0 (Romeo ist von Julias eigenen Gefühlen und Gefühlen umgeben.)
2. Narzisstischer Typ: a> 0, b <0 (Romeo ist mehr von seinen eigenen Gefühlen umgeben, er ist losgelöst von Julias Gefühlen.)
3. Vorsichtiger (oder zuverlässiger Liebhaber): a <0, b> 0 (Romeo entfernt sich von seinen eigenen Gefühlen, wird aber von Julias Gefühlen überwältigt.)
4. Einsiedler: a <0, b <0 (Romeo ist losgelöst von Julias eigenen Gefühlen und Gefühlen.)

Da für Julia auch vier Verhaltensstile möglich sind, gibt es 16 mögliche Kombinationen von Paaren mit jeweils eigener Dynamik, obwohl die Hälfte davon einer Permutation von R und J entspricht.

Die Gleichungen (1) bestimmen einen einzelnen Gleichgewichtspunkt für R = J = 0, der einer gegenseitig gleichgültigen Beziehung entspricht, oder das sogenannte „Liebesplateau“ (im Rinaldi-Modell, 1988) mit einer Beschreibung des Verhaltens durch Eigenwerte (2).




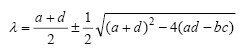
Focus Gabel Sattel
Abb. 1. Die dynamische Situation in der Nähe des Gleichgewichtspunkts im zweidimensionalen Raum gemäß Gleichung 1.

Dreieck der Liebe

Ein mathematisch reichhaltigeres Modell wird erhalten, wenn eine dritte Person zu einem einfachen Modell hinzugefügt wird, insbesondere weil es möglich ist, dass sich Allianzen bilden, in denen sich zwei Individuen gegen die dritte vereinigen können. Angenommen, Romeo hat einen anderen Liebhaber, Genevieve, obwohl die dritte fragliche Person ein Kind oder ein anderer Verwandter sein könnte. In diesem Fall wird der Zustandsraum eher sechsdimensional als zweidimensional, da jeder der drei Gefühle für die anderen beiden hat und zwölf Parameter auftreten, wenn jeder unterschiedliche Stile in Bezug auf den anderen annehmen kann, selbst wenn die natürliche Anziehungskraft ignoriert wird ( rezensiert von Rinaldi, 1998a).

Im einfachsten Fall wissen Juliet und Genevieve möglicherweise nichts über die Existenz des anderen, und Romeo zeigt möglicherweise in Bezug auf beide den gleichen romantischen Stil. Das resultierende vierdimensionale System wird dann in zwei geteilte zweidimensionale Systeme umgewandelt, bis Romeos Gefühle für Julia irgendwie von Genevieve's Gefühlen für ihn beeinflusst werden, und dasselbe gilt für Genevieve.

Nichtlineare Effekte

Es gibt unendlich viele Möglichkeiten, nichtlineare Effekte einzugeben. Stellen Sie sich vor, Romeo reagiert positiv auf Julias Liebe, aber mit einer übermäßigen Manifestation ihrer Liebe fühlt er sich wie erwürgt und zeigt eine negative Reaktion. Umgekehrt kann Romeo, wenn Julia genug Abneigung zeigt, versuchen, ihr angenehm zu werden.

In diesem Fall ist es möglich, bJ in Gleichung 1 durch die logistische Funktion bJ (1 - | J |) zu ersetzen, die der Messung von J in Einheiten entspricht, unter der Bedingung, dass J = 1 dem Wert entspricht, bei dem ihre Liebe kontraproduktiv wird. Qualitativ ähnliche Ergebnisse ergeben sich aus der Funktion bJ (1 - J2), die von Rinaldi (1998b) für das italienische Dichterplatonische Liebesmodell des 14. Jahrhunderts für die schöne Laura, gebunden durch die Ehe, betrachtet wird. Wenn wir dasselbe für Julia annehmen, erhalten wir:
(4)



Es gibt 4 Gleichgewichtszustände, darunter einen am Ursprung. Abbildung 3 zeigt den stetigen Fokus, bei dem Julia. als „leidenschaftliche Wünsche“ (c = d = 1) führt Romeos „Einsiedler“ (a = b = –2) zu einem Zustand gegenseitiger Liebe bei R = J = 2. Ein ähnliches Modell für vorsichtige (zuverlässige) Liebhaber mit sigmoidaler Nichtlinearität führt auch zu stabiles Gleichgewicht (Rinaldi und Gragnani 1998). Die Gleichungen 4 erlauben offensichtlich keine Grenzzyklen, und es tritt kein Chaos auf, während das System zweidimensional ist.


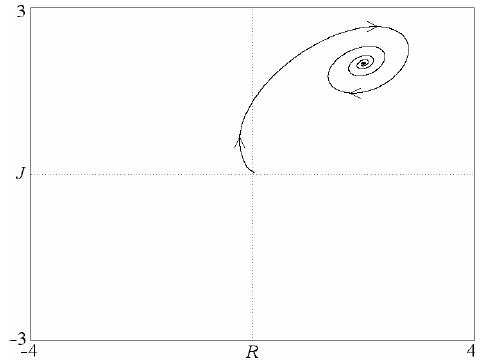Abb. 3. Eine der Lösungen für das nichtlineare Modell gemäß Gleichung 4.

Vielleicht die Anwendung nichtlinearer Effekte auf Liebesdreiecke.

Nachwort

Einige der linearen dynamischen Liebesmodelle weisen eine überraschend komplexe Dynamik auf, während viele von ihnen bekannten Erfahrungen in Beziehungen zu ähneln scheinen. Wenn drei oder mehr Variablen vorhanden sind und selbst die einfachsten nichtlinearen Effekte eingeführt werden, kann Chaos auftreten. Eine interessante Erweiterung des Modells kann man sich vorstellen, wenn man eine Gruppe interagierender Persönlichkeiten betrachtet, zum Beispiel für Fälle einer großen Familie oder Gemeinde. Solche Modelle sind natürlich sehr vereinfacht, da Liebe als einfache skalare Variable berücksichtigt wird und die Reaktionen von Individuen in Bezug auf ihre eigene Liebe und die Liebe anderer Persönlichkeiten für sie konsistent und mechanistisch sind, ohne externe Einflussfaktoren zu berücksichtigen.

PS Liebe kann ohne Mathematik leben, aber Mathematik ruft die Liebe zu sich selbst für Menschen hervor, die wahre Harmonie schätzen.

Referenzen:
Julien Clinton Sprott. Dynamische Modelle der Liebe. Nichtlineare Dynamik Psychologie und Biowissenschaften • August 2004

Rinaldi, S. (1998a). Liebesdynamik: der Fall linearer Paare. Applied Mathematics and Computation, 95, 181-192.
Rinaldi, S. & amp; Gragnani, A. (1998). Liebesdynamik zwischen sicheren Individuen: Ein Modellierungsansatz. Nichtlineare Dynamik, Psychologie und Biowissenschaften, 2, 283-301.
Rinaldi, S. (1998b). Laura und Petrarch: Ein faszinierender Fall von zyklischer Liebesdynamik. SIAM Journal on Applied Mathematics, 58, 1205-1221