Variationsinferenz - was ist das und was isst es?

Hallo Habr!

Kürzlich habe ich mit Kollegen über einen Variations-Auto-Encoder gesprochen und es stellte sich heraus, dass viele, selbst diejenigen, die in Deep Learning arbeiten, die Variations-Inferenz (Variations-Inferenz) und insbesondere die untere Variationsgrenze nur durch Hörensagen kennen und nicht vollständig verstehen, was sie ist.
In diesem Artikel möchte ich diese Probleme im Detail analysieren. Wen kümmert es, ich bitte um einen Schnitt - es wird sehr interessant sein.

Was ist Variationsinferenz?

Die Familie der Variationsmethoden des maschinellen Lernens erhielt ihren Namen aus dem Abschnitt der mathematischen Analyse „Variationsrechnung“. In diesem Abschnitt untersuchen wir die Probleme bei der Suche nach Extrema von Funktionalen (eine Funktion ist eine Funktion von Funktionen - das heißt, wir suchen nicht nach den Werten von Variablen, bei denen die Funktion ihr Maximum (Minimum) erreicht, sondern nach einer solchen Funktion, bei der die Funktion ihr Maximum (Minimum) erreicht.

Es stellt sich jedoch die Frage: Beim maschinellen Lernen suchen wir immer nach einem Punkt im Raum der Parameter (Variablen), an dem die Verlustfunktion einen Mindestwert hat. Das heißt, es ist die Aufgabe der klassischen mathematischen Analyse, und hier ist die Variationsrechnung? Die Variationsrechnung erscheint in dem Moment, in dem wir die Verlustfunktion unter Verwendung der Methoden der Variationsrechnung in eine andere Verlustfunktion umwandeln (häufig ist dies die untere Variationsgrenze).

Warum brauchen wir das? Ist es nicht möglich, die Verlustfunktion direkt zu optimieren? Wir brauchen diese Methoden, wenn es unmöglich ist, direkt eine unverzerrte Gradientenschätzung zu erhalten (oder diese Schätzung eine sehr hohe Streuung aufweist). Zum Beispiel unsere Modellsätze $$$p (z)$und $$$p (x / z)$und wir müssen berechnen $$$p (x) = \ int (p (z) p (x / z) dz)$. Genau dafür wurde der Variations-Auto-Encoder entwickelt.

Was ist die Variationsuntergrenze?

Stellen Sie sich vor, wir haben eine Funktion $$$f (x)$. Die Untergrenze für diese Funktion ist eine beliebige Funktion $$$g (x)$die Gleichung erfüllen:

$$

$$g (x) <= f (x)$$

Das heißt, für jede Funktion gibt es unzählige Untergrenzen. Sind alle diese Untergrenzen gleich? Natürlich nicht. Wir führen ein anderes Konzept ein - Diskrepanz (ich habe in der russischsprachigen Literatur keinen etablierten Begriff gefunden, dieser Wert wird in englischsprachigen Artikeln als Enge bezeichnet):

$$

$$\ delta = max {f (x)} - max {g (x)}$$

Offensichtlich ist der Rest immer positiv. Je kleiner der Rest, desto besser.

Hier ist ein Beispiel für eine Untergrenze mit dem Rest Null:

Und hier ist ein Beispiel mit einem kleinen, aber positiven Residuum:

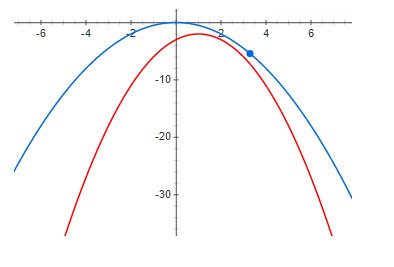
Und schließlich eine ausreichend große Diskrepanz:


Aus den obigen Diagrammen ist klar ersichtlich, dass sich bei einem Rest von Null das Maximum der Funktion und das Maximum der unteren Grenze am selben Punkt befinden. Das heißt, wenn wir das Maximum einer Funktion finden wollen, können wir nach dem Maximum der unteren Grenze suchen. Wenn die Diskrepanz nicht Null ist, ist dies nicht der Fall. Und das Maximum der unteren Grenze kann sehr weit (entlang der x-Achse) vom gewünschten Maximum entfernt sein. Die Grafiken zeigen, dass die Höhen umso weiter voneinander entfernt sein können, je größer der Rest ist. Dies ist im Allgemeinen nicht wahr, aber in den meisten praktischen Fällen funktioniert diese Intuition sehr gut.

Variabler Auto Encoder

Jetzt werden wir ein Beispiel einer sehr guten unteren Variationsgrenze mit einem potenziell Null-Residuum analysieren (darunter wird klar sein, warum) - dies ist ein Variations-Autoencoder.

Unsere Aufgabe ist es, ein generatives Modell zu erstellen und es mit der Maximum-Likelihood-Methode zu trainieren. Das Modell hat die folgende Form:

$$

$$q (x) = \ int {q (z) q_ \ theta (x | z) dz}$$

wo $$$q (x)$Ist die Wahrscheinlichkeitsdichte der erzeugten Proben, $$$z$- latente Variablen, $$$q (z)$- die Wahrscheinlichkeitsdichte einer latenten Variablen (oft eine einfache - zum Beispiel eine mehrdimensionale Gaußsche Verteilung mit Nullerwartung und Einheitsdispersion - im Allgemeinen etwas, aus dem wir leicht eine Stichprobe ziehen können), $$$q_ \ theta (x | z)$- Bedingte Probendichte für einen bestimmten Wert latenter Variablen wird im Variations-Autoencoder ein Gaußscher mit mattenerwartung und Streuung in Abhängigkeit von z ausgewählt.

Warum müssen wir die Datendichte möglicherweise so komplex darstellen? Die Antwort ist einfach: Die Daten haben eine sehr komplexe Dichtefunktion und wir können ein Modell einer solchen Dichte einfach nicht direkt technisch erstellen. Wir hoffen, dass diese komplexe Dichte mit zwei einfacheren Dichten gut angenähert werden kann. $$$q (z)$und $$$q_ \ theta (x | z)$.

Wir wollen folgende Funktion maximieren:

$$

$$I = \ int {p (x) log (q (x)) dx}$$

wo $$$p (x)$- Datenwahrscheinlichkeitsdichte. Das Hauptproblem ist, dass die Dichte $$$q (x)$(bei ausreichend flexiblen Modellen) ist es nicht möglich, das Modell analytisch darzustellen und entsprechend zu trainieren.

Wir verwenden die Bayes-Formel und schreiben unsere Funktion wie folgt um:

$$

$$I = \ int {p (x) log (\ frac {q (z) q (x | z)} {q (z | x)}) dx}$$

Leider, $$$q (z / x)$alles ist auch schwer zu berechnen (es ist unmöglich, das Integral analytisch zu nehmen). Zunächst stellen wir jedoch fest, dass der Ausdruck unter dem Logarithmus nicht von z abhängt, sodass wir die mathematische Erwartung aus dem Logarithmus in z jeder Verteilung entnehmen können. Dies ändert den Wert der Funktion nicht und multipliziert und dividiert durch den Logarithmus mit derselben Verteilung (formal haben wir nur eine Bedingung - Diese Verteilung sollte nirgendwo verschwinden. Als Ergebnis erhalten wir:

$$

$$I = \ int {p (x) dx \ int {\ phi (z | x) log (\ frac {q (z) q (x | z)} {\ phi (z | x)})}} + \ int {p (x) dx \ int {\ phi (z | x) log (\ frac {\ phi (z | x)} {q (z | x)})}}$$

Beachten Sie, dass der zweite Term erstens die KL-Divergenz ist (was bedeutet, dass er immer positiv ist):

$$

$$I = \ int {p (x) dx \ int {\ phi (z | x) log (\ frac {q (z) q (x | z)} {\ phi (z | x)})}} + \ int {p (x) KL [\ phi (z | x) || q (z | x))] dx}$$

und zweitens $$$I$hängt nicht davon ab $$$q (z | x)$nicht von $$$\ phi (z | x)$. Daraus folgt, dass

$$

$$I> = \ int {p (x) dx \ int {\ phi (z | x) log (\ frac {q (z) q (x | z)} {\ phi (z | x)})}} = VLB$$

wo $$$Vlb$- Die untere Variationsgrenze (Variationsuntergrenze) und erreicht ihr Maximum, wenn $$$KL [\ phi (z | x) || q (z | x))] = 0$- d.h. die Verteilungen sind gleich.

Positivität und Gleichheit auf Null genau dann, wenn die Verteilungen mit KL-Divergenzen übereinstimmen, werden durch Variationsmethoden genau bewiesen - daher der Name Variationsgrenze.

Ich möchte darauf hinweisen, dass die Verwendung einer Variationsuntergrenze mehrere Vorteile bietet. Erstens gibt es uns die Möglichkeit, die Verlustfunktion durch Gradientenmethoden zu optimieren (versuchen Sie dies, wenn das Integral nicht analytisch genommen wird), und zweitens approximiert es die inverse Verteilung $$$q (z | x)$Verteilung $$$\ phi (z | x)$- das heißt, wir können nicht nur Daten, sondern auch latente Variablen abtasten. Leider ist der Hauptnachteil, wenn das inverse Verteilungsmodell nicht flexibel ist, d. H. Wenn die Familie $$$\ phi (z | x)$enthält nicht $$$q (z | x)$- Der Rest ist positiv und gleich:

$$

$$\ delta = \ int {p (x) \ underset {\ phi (z | x)} {min} (KL [\ phi (z | x) || q (z | x)]) dx}$$

und dies bedeutet, dass das Maximum der unteren Grenze und die Verlustfunktionen höchstwahrscheinlich nicht zusammenfallen. Übrigens erzeugt der Variations-Auto-Encoder, der zum Generieren von Bildern verwendet wird, Bilder, die zu verschwommen sind. Ich denke, das liegt nur an der Wahl einer zu armen Familie $$$\ phi (z | x)$.

Ein Beispiel für ein nicht so gutes Endergebnis

Wir werden nun ein Beispiel betrachten, bei dem einerseits die untere Grenze alle guten Eigenschaften aufweist (bei einem ausreichend flexiblen Modell ist der Rest Null), aber wiederum keinen Vorteil gegenüber der Verwendung der ursprünglichen Verlustfunktion bietet. Ich glaube, dass dieses Beispiel sehr aufschlussreich ist. Wenn Sie keine theoretische Analyse durchführen, können Sie viel Zeit damit verbringen, Modelle zu trainieren, die keinen Sinn ergeben. Modelle sind eher sinnvoll, aber wenn wir ein solches Modell trainieren können, ist die Auswahl einfacher $$$q (x)$aus derselben Familie und verwenden Sie das Maximum-Likelihood-Prinzip direkt.

Wir betrachten also genau das gleiche generative Modell wie im Fall eines Variations-Auto-Encoders:

$$

$$q (x) = \ int {q (z) q_ \ theta (x | z) dz}$$

Wir werden mit der gleichen Maximum-Likelihood-Methode trainieren:

$$

$$I = \ int {p (x) log (q (x)) dx}$$

Wir hoffen das immer noch $$$q (x | z)$Es wird viel "einfacher" sein als $$$q (x)$.
Erst jetzt werden wir schreiben $$$I$ein bisschen anders:

$$

$$I = \ int {p (x) log (\ int {q (z) q_ \ theta (x | z) dz}) dx}$$

Mit der Jensen-Formel erhalten wir:

$$

$$I> = \ int {p (x) q (z) log (q_ \ theta (x | z)) dxdz} = VLB$$

Genau in diesem Moment reagieren die meisten Menschen, ohne zu glauben, dass dies wirklich das Endergebnis ist und Sie das Modell trainieren können. Dies ist wahr, aber schauen wir uns die Diskrepanz an:

$$

$$\ delta = \ int {p (x) log (q (x)) dx} - \ int {p (x) q (z) log (q_ \ theta (x | z)) dxdz}$$

wo (durch zweimaliges Anwenden der Bayes-Formel):

$$

$$\ delta = \ int {p (x) q (z) log (\ frac {q (x)} {q (x | z)}) dxdz} = \ int {p (x) q (z) log ( \ frac {q (z)} {q (z | x)}) dxdz}$$

es ist leicht zu sehen, dass:

$$

$$\ delta = \ int {p (x) KL [q (z) || q (z | x)] dx}$$

Mal sehen, was passiert, wenn wir die untere Grenze erhöhen - der Rest wird abnehmen. Mit einem ziemlich flexiblen Modell:

$$

$$KL [q (z) || q (z | x)] \ rightarrow0$$

Alles scheint in Ordnung zu sein - die untere Grenze hat einen Rest von potenziell Null und ein ziemlich flexibles Modell $$$q (x | z)$alles sollte funktionieren. Ja, das ist wahr, nur aufmerksame Leser können feststellen, dass wenn kein Residuum erreicht wird $$$x$und $$$z$sind unabhängige Zufallsvariablen !!! und für ein gutes Ergebnis die „Komplexität“ der Verteilung $$$q (x | z)$sollte nicht weniger sein als $$$q (x)$. Das heißt, die untere Grenze bringt uns keine Vorteile.

Schlussfolgerungen

Die untere Variationsgrenze ist ein hervorragendes mathematisches Werkzeug, mit dem Sie „unbequeme“ Funktionen für das Lernen näherungsweise optimieren können. Aber wie bei jedem anderen Werkzeug müssen Sie die Vor- und Nachteile sehr gut verstehen und auch sehr vorsichtig verwenden. Wir haben ein sehr gutes Beispiel betrachtet - einen Variations-Auto-Encoder sowie ein Beispiel für eine nicht sehr gute untere Grenze, während die Probleme dieser unteren Grenze ohne eine detaillierte mathematische Analyse schwer zu erkennen sind.

Ich hoffe es war zumindest ein wenig nützlich und interessant.