Die Bedeutung von Primzahlen sowohl im täglichen Gebrauch als auch in allen Bereichen der Mathematik kann nicht überschätzt werden . Wir verlassen uns ruhig auf ihre besonderen Eigenschaften und nutzen sie als Grundlage für unzählige Elemente unserer Gesellschaft, weil sie ein unteilbarer Bestandteil des Naturgefüges sind. Primzahlen, die gegen jede Faktorisierung resistent sind, werden oft als "Atome" der Welt der Mathematik bezeichnet. Carl Sagan sagte über sie so:

Der Status von Primzahlen als Grundbausteine ​​aller Zahlen, die selbst die Bausteine ​​unseres Verständnisses des Universums sind, ist sehr wichtig.

In der Natur und in unserem Leben werden überall Primzahlen verwendet : Zikaden bauen ihre Lebenszyklen darauf auf, Uhrmacher verwenden sie zur Berechnung von Zecken, und in Flugzeugtriebwerken wird mit ihrer Hilfe die Frequenz der Luftimpulse ausgeglichen. Alle diese Anwendungsbereiche verblassen jedoch vor dem Hintergrund einer Tatsache, die jedem Kryptographen bekannt ist: Primzahlen sind das Herzstück der modernen Computersicherheit, dh sie sind direkt für den Schutz von allem verantwortlich . Sehen Sie die Sperre in der Adressleiste des Browsers? Ja, dies bedeutet, dass ein Zwei-Tasten-Handshake verwendet wird, der auf Primzahlen basiert. Wie ist Ihre Kreditkarte beim Einkaufen geschützt? Auch mit Kryptographie basierend auf Primzahlen.

Trotz der Tatsache, dass wir uns ständig auf ihre einzigartigen Eigenschaften verlassen, blieben uns Primzahlen schwer fassbar. Während der gesamten Geschichte der Mathematik haben die größten Köpfe versucht, einen Satz zur Vorhersage von Zahlen zu beweisen, die Primzahlen sind oder wie weit sie voneinander entfernt sein sollten. Tatsächlich sind einige ungelöste Probleme, wie das Problem der Zwillingszahlen , das Goldbach-Problem , Palindrom-Primzahlen und die Riemann-Hypothese , mit dieser allgemeinen Unvorhersehbarkeit und Unsicherheit von Primzahlen verbunden, wenn sie zur Unendlichkeit neigen. Natürlich haben wir seit Euklid Algorithmen entdeckt, mit denen wir die Position einiger Zahlen vorhersagen können, aber die allgemeinen Theoreme wurden noch nicht bewiesen, und frühere Versuche hatten keine Werkzeuge zur Überprüfung großer Zahlen. Die Technologie des 21. Jahrhunderts ermöglicht es Forschern jedoch, Annahmen an extrem großen Zahlen zu testen. Diese Technik allein ist jedoch umstritten, da ein grobes Screening nicht als verlässlicher Beweis angesehen wird. Mit anderen Worten, Primzahlen widersetzen sich jeder universellen Formel oder Gleichung, und ihre Anordnung in der Natur scheint zufällig zu sein.

Eine Person mit zufälligen Kritzeleien konnte jedoch beweisen, dass sie zumindest nicht vollständig zufällig sind ...

Vom Schnörkel bis zur Spitze - Ulam Tischdecke

Einer der größten Beweise dafür, dass die Anordnung der Primzahlen kein reiner Zufall ist, erschien auf die unwahrscheinlichste Weise: aus gedankenlosen und zufälligen Kritzeleien eines gelangweilten Vorlesungsstudenten.


Tischdecke Ulam

Der polnische Mathematiker Stanislav Ulam entdeckte dieses grafische Muster 1963 während eines Seminars. Er zeichnete ein Gitter von Linien, beschloss, die Schnittpunkte in einem Quadrat-Spiral-Muster zu nummerieren, und begann, die Zahlen in Spiralen zu kreisen, die einfach waren. Zu seiner Überraschung fielen die eingekreisten Primzahlen auf diagonale gerade Linien oder zeigten, wie Ulam es etwas strenger ausdrückte, "stark nicht zufälliges Verhalten". Ulams Tischdecke oder Spirale aus Primzahlen ist die resultierende grafische Darstellung des Satzes von Primzahlen, die in einer quadratischen Spirale markiert sind. Die Tischdecke wurde ursprünglich veröffentlicht und wurde in der Überschrift "Mathematical Games" von Martin Gardner in Scientific American weithin bekannt.


Ulam Tischdecke mit den Maßen 377x377 (Zahlen bis zu 142.000)

Die oben gezeigte Visualisierung zeigt offensichtlich bemerkenswerte Muster, insbesondere entlang der Diagonalen. Aber vielleicht täuschen wir uns selbst? Es wird oft behauptet, dass Ulams Tischdecke nur ein Trick unseres Gehirns ist, der versucht, zufällige Muster zu finden. Glücklicherweise können wir zwei verschiedene Techniken verwenden, um sicherzustellen, dass dies nicht der Fall ist. Sowohl der visuelle Vergleich als auch die logische Analyse zeigen definitiv, dass das Muster nicht zufällig ist. Zunächst vergleichen wir die durch eine Matrix der Größe NxN definierte Ulam-Tischdecke mit einer Matrix derselben Größe, die zufällig definierte Punkte enthält. Zweitens können wir unser Wissen über Polynome nutzen, um zu verstehen, warum bei der grafischen Darstellung von Primzahlen ein Muster auftreten sollte .

Wie oben erwähnt, wird die intuitivste Bestätigung der Nicht-Zufälligkeit des Musters höchstwahrscheinlich ein direkter Vergleich mit der Tischdecke von Ulam sein. Erstellen Sie dazu eine Ulam-Tischdecke und eine quadratische Spirale mit zufälligen Positionen gleicher Größe. Nachfolgend sind zwei verschiedene 200x200-Matrizen dargestellt, die numerische Spiralen darstellen:


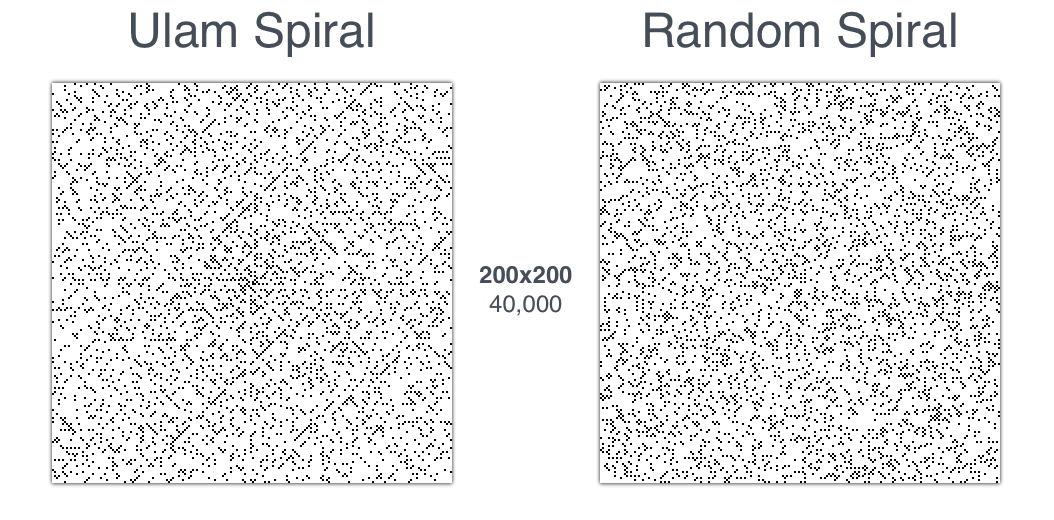
Ein visueller Vergleich macht ziemlich deutlich, dass Ulams Tischdecke atemberaubende Muster enthält, insbesondere entlang der diagonalen Achsen. Darüber hinaus gibt es fast keine Punktcluster. Andererseits erzeugt die zufällige Anordnung von Punkten nicht sofort erkennbare Muster und führt zur Ansammlung von Punkten in verschiedene Richtungen. Zweifellos fehlt einer solchen Technik die Strenge traditioneller Beweise; Die Visualisierung von Spiralen von Primzahlen hat jedoch etwas Makelloses: Dies ist eine zufällig entdeckte Technik, mit der Sie einen Graphen erstellen können, der die Logik stimuliert und ästhetisch attraktiv ist.

Wenn wir uns der Natur von Primzahlen logischer und traditioneller nähern, ist es durchaus vernünftig, das Auftreten von Mustern in solchen Visualisierungen zu erwarten. Wie oben erwähnt, scheinen die Linien in diagonaler, horizontaler und vertikaler Richtung einen Hinweis zu enthalten. Einige dieser Linien, die keine Primzahlen sind, können durch gewöhnliche quadratische Polynome erklärt werden, die die Möglichkeit des Auftretens von Primzahlen ausschließen - zum Beispiel schließt eine der diagonalen Linien, die der Gleichung y = x² entsprechen, Primzahlen offensichtlich aus. Andererseits ist bekannt, dass einige quadratische Polynome, sogenannte Primformeln (wir werden weiter unten darauf eingehen), eine hohe Dichte von Primzahlen erzeugen, beispielsweise das Euler-Primpolynom: x² - x - 41; Dies ist eine weitere Linie, die sich als Muster in einer Spirale widerspiegelt (obwohl es schwierig ist, Lücken im obigen Diagramm zu finden).

Ein visueller Vergleich zeigt Muster an und eine logische Analyse bestätigt das Vorhandensein erwarteter Muster. Natürlich sind wir noch weit von einer universellen Formel entfernt, um alle Primzahlen zu finden, aber Ulams Tischdecke ist zweifellos schön, sowohl als Symbol unseres Wissens als auch als Meisterwerk der natürlichen Kunst.

Sachs Spirale

Wie in vielen Bereichen der Mathematik begann die Armee der in die Fußstapfen getretenen Mathematiker nach dem Aufkommen der ursprünglichen Idee Versuche, einen Beitrag zum neuen Thema zu leisten. Es ist logisch, dass Ulams Tischdecke Generationen von Mathematikern inspirierte, die versuchten, seinen erstaunlichen Fund zu entwickeln. 1994 beschloss der Softwareentwickler Robert Sachs, seine Programmierkenntnisse zu nutzen, um Primzahlen auf verschiedene Arten zu visualisieren.

Fast wie bei Ulams Tischdecke beschloss Sachs, sein Schema mit einer anderen Spiralebene zu strukturieren. Ähnlich wie bei der oben gezeigten quadratischen Spirale weigern sich Spiralebenen, dem traditionellen kartesischen Zahlensystem Punkte zu geben, da sie ein unipolares Positionierungssystem sind. Wenn Sie nur die Zahl kennen, können Sie ihre Position in der Spirale, ihre Position relativ zu allen anderen Zahlen in der Spirale sowie den Abstand von ihr zum vorherigen und nächsten Quadrat der Zahl herausfinden. Anstelle einer quadratischen Spirale versuchte Sax jedoch, Muster mit ganzen Zahlen zu finden, die einer archimedischen Spirale mit den folgenden Polarkoordinaten überlagert waren:


Polarkoordinaten der Spirale von Archimedes / Sachs

Bei dieser Technik wird die archimedische Spirale um Null zentriert, und die Quadrate aller natürlichen Zahlen (1,4,9,16,25) befinden sich an den Schnittpunkten der Spirale und der Polarachse (östlich des Ursprungs).


Archimedes / Sax Spiralstruktur

Nachdem wir dieses Diagramm erstellt haben, füllen wir die Punkte zwischen den Quadraten entlang der Spirale (gegen den Uhrzeigersinn) und wenden sie in gleichem Abstand voneinander an. Und am Ende werden wir, wie im Beispiel mit Ulams Tischdecke, die in der resultierenden Spirale enthaltenen Primzahlen herausgreifen.

Die 2003 erstmals online veröffentlichte numerische Spirale von Sachs ist sowohl optisch als auch intellektuell attraktiv. Darüber hinaus erhalten wir, wie wir gleich sehen werden, ein tieferes Verständnis der Grundmuster als die bekannte Ulam-Tischdecke , da sie die gestrichelten Linien der Ulam- Pseudospirale kombiniert:


Archimedische Spirale mit markierten Primzahlen, es ist auch die Sax-Spirale.

Das resultierende Diagramm zeigt erneut auffällige Muster. Fast sofort wird klar, dass von der Mitte eine saubere weiße Linie verläuft, die sich horizontal nach Osten erstreckt. Wenn wir uns unserem Schema zuwenden, können wir sicherstellen, dass dies nur eine Linie ist, die alle Quadrate von ganzen Zahlen enthält (r = n ^ (. 5)). Zweite Beobachtung: Das Markierungsmuster ähnelt im Gegensatz zu den geraden Linien der Ulam-Tischdecke eher gekrümmten Linien . Es stellt sich heraus, dass diese Kurven, auch Produktkurven genannt , zu Polynomen zurückkehren, die die Muster erklären, die in der vorherigen Spirale auftreten. Aber bevor wir uns ihnen zuwenden, vergleichen wir aus Gründen der Einheit noch einmal die Sachs-Spirale mit der Spirale der Zufallswerte:

Polynome und Produktkurven

Die Arbeit von Robert Sachs nach dieser Entdeckung konzentrierte sich ausschließlich auf diese krummen Stücke , die in oder nahe der Mitte der Spirale beginnen und sich in verschiedenen Winkeln mit den Windungen der Spirale schneiden. Die Kurven sind fast gerade, aber typischer für sie ist, dass sie teilweise, vollständig oder mehrfach im Uhrzeigersinn (gegen die Bewegung der Spirale selbst) um den Ursprung drehen, bevor sie in einem bestimmten Versatz von der Ost-West-Achse begradigt werden. Einer der auffälligsten Aspekte der numerischen Sachs-Spirale ist das Überwiegen solcher gekrümmter Werke auf der westlichen Hemisphäre (auf der dem Quadrat der Zahlen gegenüberliegenden Seite).

Sachs beschrieb Produktkurven als "Produkte von Faktoren mit einem konstanten Unterschied zwischen ihnen". Mit anderen Worten, jede Kurve kann durch eine quadratische Gleichung (Polynom zweiten Grades) dargestellt werden, was wiederum kein einfacher Zufall ist, da das Quadrat einer natürlichen Zahl in der Sachs-Spirale vorherrscht. Vielleicht können diese Produktkurven zu dem Schluss führen, dass die Sachs-Spirale auf unserem Weg zum Verständnis von Primzahlen viel nützlicher ist als Ulams Tischdecke. Obwohl Ulams Tischdecke uns die Muster und die mögliche Existenz von Gleichungen zeigte, gibt die Sachs-Spirale Stützpunkte bei der Suche nach Primformeln - ihre Krümmung und Integrität sind konstant, was bedeutet, dass sie viel einfacher zu erkennen sind. Zum Beispiel enthält die unten gezeigte Sachs-Spirale beschriftete Linien und ihre entsprechende Primformel, die in Standardform geschrieben sind. Wie ich versprochen habe, hat uns die berühmte Euler-Formel zur Erzeugung von Primzahlen wieder getroffen (letzter Eintrag: n² + n +41):


Dank dieser Zahlenspirale konnte Sax eine beeindruckende Aussage darüber machen, was eine Primzahl ist: eine positive ganze Zahl, die nur auf einer Kurve des Produkts liegt. Da sich die Spirale endlos drehen kann, können die Kurven selbst auch als endlos betrachtet werden. Theoretisch können diese Produktkurven möglicherweise den Ort ausreichend großer Zahlen vorhersagen - zumindest solche Zahlen sind einen genaueren Blick wert.

Insgesamt hat uns die Sachs-Spirale zweifellos zu einem tieferen Verständnis der Primzahlen geführt, indem wir bequemere Formeln für Primzahlen vorgeschlagen haben.

Bedeutung von allem

Also haben wir sowohl die Tischdecke von Ulam als auch die Sax-Spirale analysiert. Durch diese Beispiele hat sich unser Verständnis der Natur der Primzahlen erweitert. Insbesondere die Sachs-Spirale führte uns in Produktkurven ein, die im Wesentlichen aus quadratischen Gleichungen bestehen, die als Primformeln bezeichnet werden. Beide Grafiken, sowohl Ulama als auch Sax, erwiesen sich als unerwartet und ästhetisch. Sie regen unsere Neugier an und beleuchten eine der schwierigsten Aufgaben für die ganze Welt.

Welche Lektion kann man daraus lernen?

Sie können es niemals ablehnen, scheinbar unlösbare Probleme zu überprüfen, selbst wenn Sie dies aus purer Neugier und Langeweile tun. Jeder kann Entdeckungen machen und oft entstehen sie durch völlig ungewöhnliche Prozesse. Stanislav Ulam änderte dank der Visualisierung die Sichtweise auf die berühmte Aufgabe und kam dem Verständnis der Primzahlen einen Schritt näher: Wer weiß, auf welche anderen unerwarteten Entdeckungen wir stoßen werden?