Formel zur Berechnung von Primzahlen und zur Optimierung von Brute-Force-Teilern

Grüße! Ich beschloss nach Belieben, das Problem der Suche nach Primzahlen zu untersuchen. Das Thema ist umfangreich und interessant. Ich möchte ein paar Gedanken darüber teilen, die mir in den Sinn kamen. Eine Suche im Internet ergab keine solchen Hinweise auf ihre Originalität.

Erstens habe ich nie eine mathematische Formel gefunden, um Primzahlen der Reihe nach zu berechnen. Wenn es jedoch Algorithmen gibt, ist es sicherlich möglich, Formeln mit logischen Funktionen oder Operatoren zu erstellen. Ich gebe unten die prägnanteste Formel an, die sich herausstellte.

Für eine Folge von Zahlen $$$(x_ {m}) = {x_ {1}, x_ {2}, x_ {3}, ... x_ {max}}$ Wir stellen den Operator der Erkennung der ersten Zahl gleich a vor:

$$

$$\ mathbf {Dt_ {a}} (x_ {m}): = \ left \ {\ begin {matrix} m \ \ mathbf {if} \ \ existiert \ m: \ forall \, k <m \ x_ {k } \ neq a \ \ mathbf {und} \ x_ {m} = a \\ 0 \ \ mathbf {andernfalls} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ end {matrix} \ right.$$

Alle Primzahlen, beginnend mit 5, können nach folgender Formel berechnet werden:

$$

$$P_ {n} = P_ {n-1} +2 \ mathbf {Dt_ {0} ^ {i}} (\ mathbf {Dt_ {0} ^ {j}} ((P_ {n-1} + 2i)) \, mod \, P_ {j + 1})), \ \ \ \ forall \, n \ geqslant 3 \\ \ forall \, i_ {max} \ geqslant \ max \ frac {P _ {\ alpha} -P_ { \ alpha -1}} {2} +10 \ ,, \ \ 2 \ leqslant \ alpha \ leqslant n-1; \ \ j_ {max} = \ pi (\ sqrt {P_ {n-1} + 2i}) - 1$$

Betreiber $$$\ mathbf {Dt_ {0} ^ {j}}$ iteriert vorbei $$$j$ der Rest der Division jeder Kandidatennummer durch Einfachheit mit $$$i$ Nummer $$$(P_ {n-1} + 2i)$ zu Primzahlen, die bereits im Bereich bis zu gefunden wurden $$$P_ {j_ {max} +1}$ . Die Kandidatennummern werden in der Reihenfolge aus dem Satz ungerader Zahlen ausgewählt, die größer als die vorherige Primzahl sind $$$P_ {n-1}$ . $$$\ pi (\ sqrt {P_ {n-1} + 2i})$ Ist eine pi-Funktion, die die Anzahl der Primzahlen anzeigt $$$\ leqslant \ sqrt {P_ {n-1} + 2i}$ .
Betreiber $$$\ mathbf {Dt_ {0} ^ {i}}$ iteriert vorbei $$$i$ Bedienerausgabewerte $$$\ mathbf {Dt_ {0} ^ {j}}$ bis es 0 findet. Da die Reihe der Primzahlen unendlich ist, wird dies früher oder später geschehen. Am Ausgang des Betreibers $$$\ mathbf {Dt_ {0} ^ {i}}$ Es wird also immer eine Nummer geben $$$i$ . Untergrenze $$$i_ {max}$ wird durch die maximale Differenz benachbarter Primzahlen bestimmt, die kleiner als die gewünschte sind. Die Zunahme dieser Differenz erfolgt logarithmisch. Die folgende Grafik zeigt die Abhängigkeit des maximalen und durchschnittlichen Wachstums $$$\ Delta P _ {\ alpha}$ von n für die ersten 100.000 Primzahlen. Der Maximalwert wurde abgetastet und für jeweils tausend Zahlen gemittelt.
Die maximale Zunahme der Differenz der Primzahlen $$$\ delta _ {max} (\ Delta P _ {\ alpha})$ zum vorherigen Maximalwert $$$max (\ Delta P _ {\ alpha})$ gleich 20 (für die Differenz der Primzahlen 31397-31469 = 72 in Bezug auf die Differenz 25523-25471 = 52). Es ist in der Region, in der die Ableitung des Hüllkurvenlogarithmus erfolgt $$$\ Delta P _ {\ alpha}$ immer noch groß genug und Primzahlen sind nicht mehr zu klein. Basierend auf diesem Wert wird die Bedingung für $$$i_ {max}$ . Grafik $$$\ delta _ {max} (\ Delta P _ {\ alpha})$ für die ersten 50.000 Primzahlen unten angegeben. Die Werte wurden für jeweils tausend berechnet.
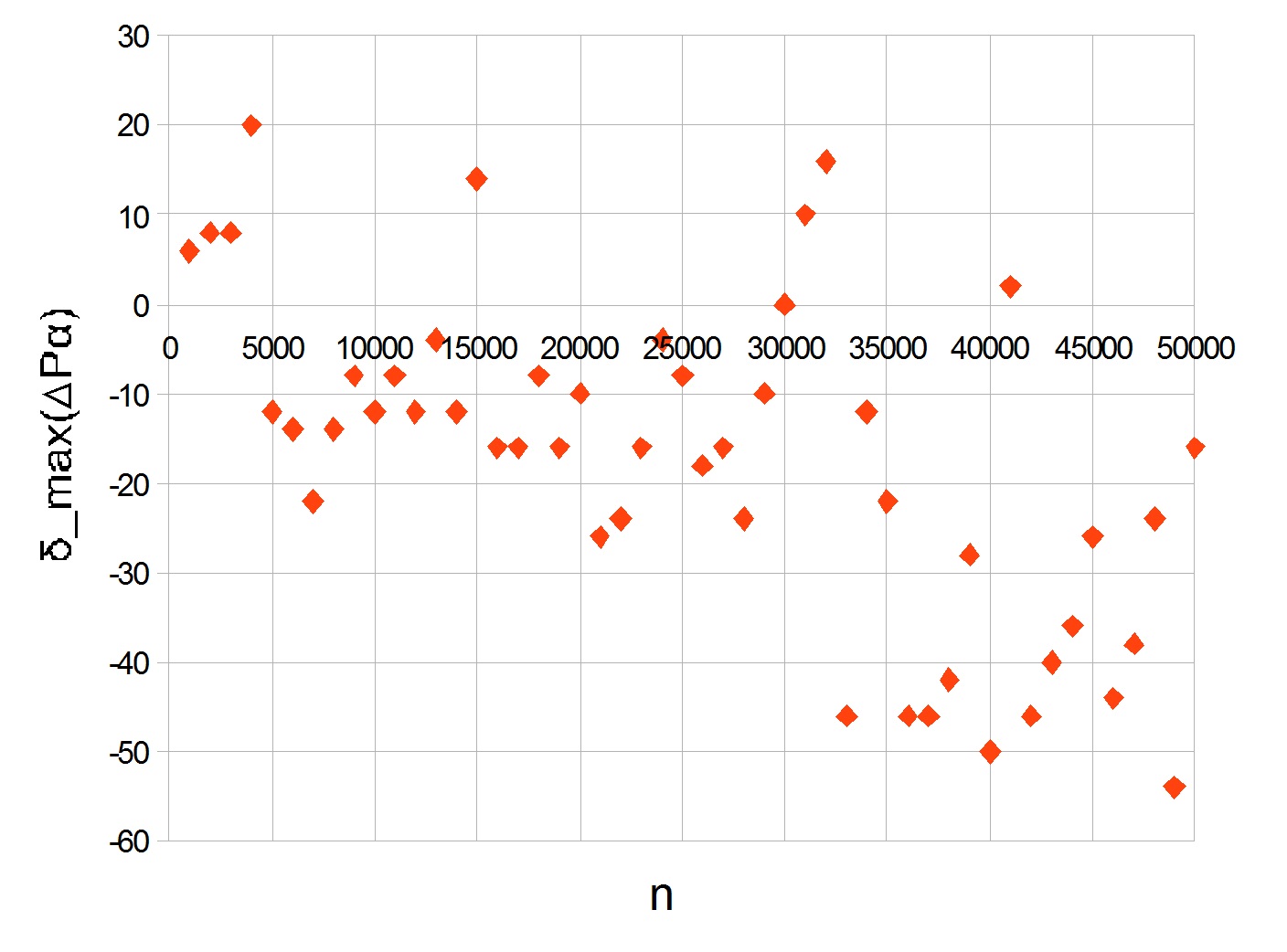
Der Peak ist bei 20 sichtbar. Mit zunehmendem n geht der Graph auf Minus und zeigt eine Abnahme der Wachstumsrate großer Primzahlen.

Die zweite Überlegung besteht darin, die Berechnung einer Folge von Primzahlen zu optimieren.
Der in der obigen Formel festgelegte Algorithmus ist eine verbesserte Methode zum Aufzählen von Teilern. Verbesserungen bestehen darin, gerade Zahlen von der Betrachtung auszuschließen und die Teilbarkeit nur von Primzahlen zu überprüfen, die kleiner als sq sind. die Wurzeln der Kandidatennummern. Der schwierigste Teil des Algorithmus ist die Berechnung des Satzes der verbleibenden Mod- Funktionen. Durch die Optimierung dieser Funktion kann die Komplexität reduziert werden. Es gibt jedoch einen noch effektiveren Weg. Lass $$$(r_ {j + 1} ^ {n-1}) = {r_ {2}, r_ {3}, ... r _ {\ pi (\ sqrt {P_ {n-1}})}}$ Ist eine Folge von Resten aus der Aufteilung der zuletzt gefundenen Primzahl in Primzahlen von 3 bis zur Wurzel. Wir werden Sequenzen der Form machen

$$

$$(r_ {i, j + 1} ^ {n}) = {(r_ {2} + 2i) \, mod \, P_2, (r_ {3} + 2i) \, mod \, P_3, ... \\ (r _ {\ pi (\ sqrt {P_ {n-1}})} + 2i) \, mod \, P _ {\ pi (\ sqrt {P_ {n-1}})}, (P_ {n -1} + 2i) \, mod \, P _ {\ pi (\ sqrt {P_ {n-1} + 2i})}}$$

in der Reihenfolge ab $$$i = 1$ . Der letzte Term wird berechnet, wenn $$$\ pi (\ sqrt {P_ {n-1} + 2i}) \ neq \ pi (\ sqrt {P_ {n-1}})$ . Wenn in einem Schritt der Berechnung der Rest $$$r_ {i, j + 1} ^ {n}$ wird gleich 0, gehe zur nächsten Sequenz. Dies geschieht, bis i gefunden wird, bei dem alle Rückstände ungleich Null sind. Dies bedeutet, die nächste Primzahl zu finden. Sequenz $$$(r_ {j + 1} ^ {n})$ Es muss gespeichert werden, bis die nächste Primzahl gefunden wird. Die wiederkehrende Formel zur Berechnung von Primzahlen auf diese Weise wird konvertiert in:

$$

$$P_ {n} = P_ {n-1} +2 \ mathbf {Dt_ {0} ^ {i}} (\ mathbf {Dt_ {0} ^ {j}} (r_ {i, j + 1} ^ { n})), \ \ \ \ forall \, n \ geqslant 3$$

In dem vorgestellten Algorithmus wird die Operation mod erleichtert: teilbar durch $$$(r_ {j + 1} + 2i) / P_ {j + 1}$ mal mehr Trennwände. Die einzigen Ausnahmen sind das Auftreten neuer einfacher Teiler. Im Computerspeicher ist es bei der Implementierung des Algorithmus erforderlich, ein Array von Primzahlen an der Wurzel des gesuchten sowie ein variables Array von Residuen zu speichern. Die Komplexität des Algorithmus im allgemeinen Sinne (der Arbeitsaufwand) kann geringer sein als die anderer bekannter Methoden. Die komplexesten Operationen darin sind die Extraktion der Quadratwurzel, die Berechnung von Resten und die Multiplikation. Die Wurzel kann auf die nächste ganze Zahl extrahiert werden. Um Rückstände zu erhalten, können Sie einen effektiven Algorithmus verwenden, der auf der allgemeinen Teilbarkeitsregel basiert. Die Multiplikation wird nur mit 2 relativ kleinen Zahlen i verwendet . Die zeitliche Komplexität des Algorithmus kann reduziert werden, indem die Arbeit gemäß den Werten von i verteilt wird . Das auf diese Weise erhaltene segmentierte Sieb sollte auf Multithread-Computern schneller funktionieren. Die geleistete Arbeit wird jedoch aufgrund der Erhöhung der Dividenden größer sein. Sie können die Radfaktorisierung auch auf den Algorithmus „schrauben“. Mit der optimalen Größe der Räder kann dies die Komplexität in einem bestimmten Bereich von n reduzieren - bis die Hardware "wild" es verlangsamt.

Vielleicht wird jemand meine Gedanken nützlich machen.