Binäre Suchbäume sind eine Datenstruktur zum Speichern von Elementen mit Schnellsuchfunktionen. Die Idee ist einfach und genial: "Weniger ist übrig, mehr ist richtig." Hier endet die Einfachheit und komplexe Fragen des Balancierens eines Baumes beginnen, damit er nicht zu einem langen Ast wird.

In diesem Artikel geben wir eine Definition, listen die Regeln für das Platzieren von Elementen in einem rot-schwarzen Baum auf, betrachten einen Ausgleichsalgorithmus und konsolidieren das, was in einem Beispiel gesagt wurde. Wir werden dieses Thema sowie andere Arten von binären Suchbäumen im Kurs „Algorithmen für Entwickler“ genauer untersuchen. Der rot-schwarze Baum
Der rot-schwarze Baum ist ein selbstausgleichender binärer Suchbaum, der eine logarithmische Erhöhung der Höhe des Baums aus der Anzahl der Knoten und die schnelle Ausführung der grundlegenden Operationen des Suchbaums garantiert: Hinzufügen, Löschen und Suchen eines Knotens.
Der rot-schwarze Baum ist nicht vollständig ausbalanciert, an einigen Stellen kann seine Höhe fast doppelt variieren. Eine solche Annahme wirkt sich nicht asymptotisch auf die Geschwindigkeit der Suche nach Elementen aus, sondern beschleunigt die Platzierung neuer Elemente erheblich, da Sie den Baum nicht jedes Mal "schütteln" müssen, wenn Sie Elemente hinzufügen. Manchmal reicht es aus, ein rotes Element hinzuzufügen, ohne die anderen zu berühren und ohne die "schwarze Höhe" zu ändern. .
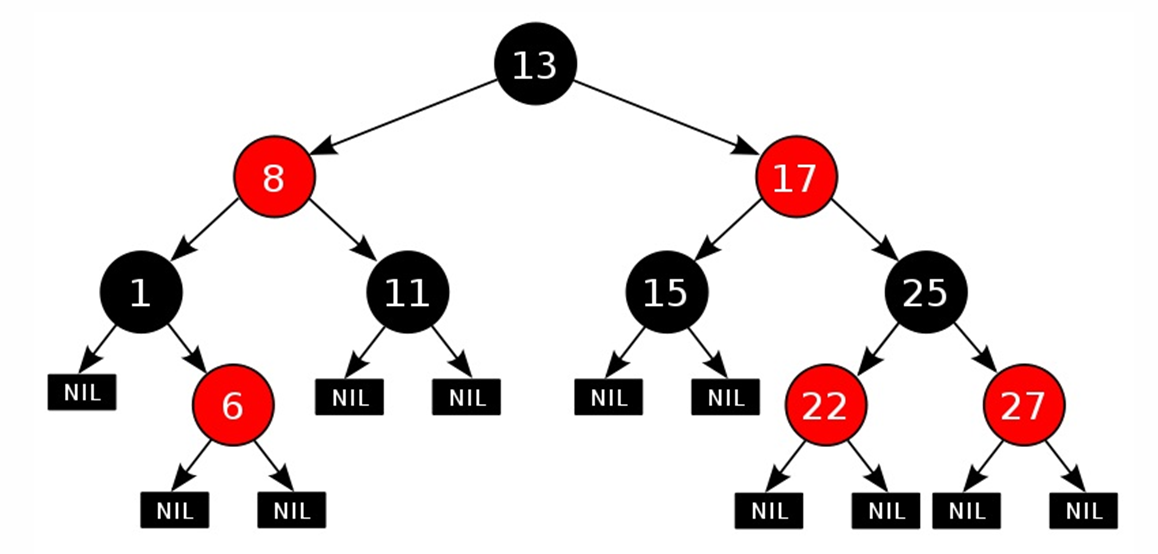
Regeln zum Platzieren von Elementen in einem rot-schwarzen Baum
- Jeder Knoten ist entweder rot oder schwarz, NIL-Blätter sind immer schwarz.
- Die Wurzel des Baumes ist immer schwarz
- Beide Nachkommen jedes roten Knotens sind schwarz
- Der Pfad von einem Knoten zu einem Nachkommenblatt enthält die gleiche Anzahl schwarzer Knoten.
Wenn Sie ein neues Element einfügen, wird ihm eine rote Farbe zugewiesen. Um die ersten beiden Regeln zu erfüllen, malen Sie einfach die neuen Scheitelpunkte in der gewünschten Farbe neu.
Beachten Sie die Ausgleichsregeln für die Umsetzung von 3 und 4 Punkten.
In jeder Abbildung wird davon ausgegangen, dass wir bereits ein Element X hinzugefügt haben, das gegen die 3-Regel verstößt. Wir müssen die Struktur des Baums ändern, damit die 3-Regel ausgeführt wird und 4 nicht gebrochen wird.
Legende der Eckpunkte:
- X - ein hinzugefügtes Element, das gegen 3 Absätze der Regeln verstößt.
- P - Papa Gegenstand X.
- G - der Großvater des Elements X, der Vater des Elements P.
- U ist der Onkel des Elements X, der Bruder des Elements P, der zweite Sohn des Elements G.
Fall Eins - Roter Onkel
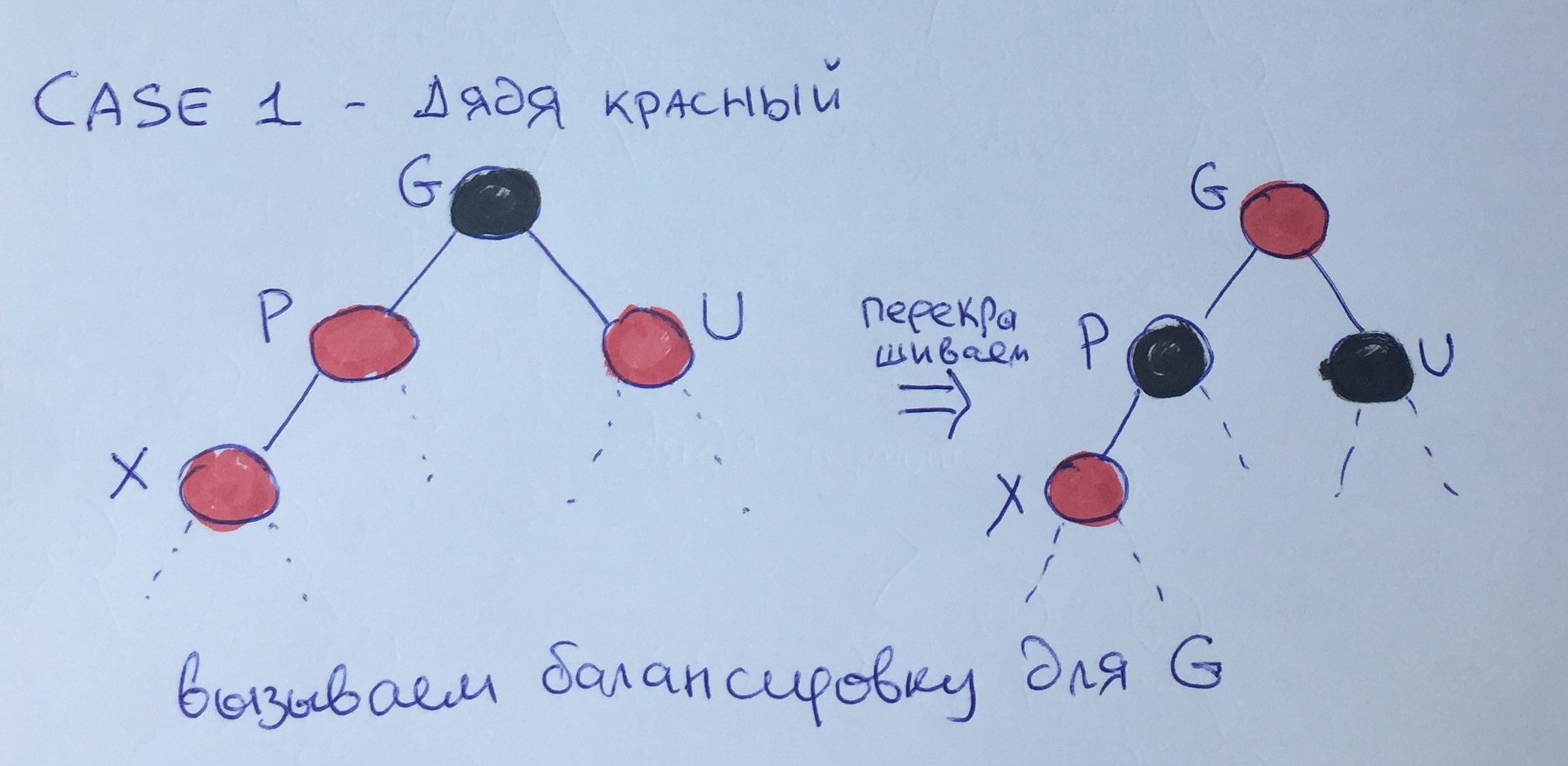
Wenn sowohl der Vater als auch der Onkel rot sind, können wir die schwarze Farbe von der Ebene des Großvaters auf die Ebene des Vaters „senken“ und die Knoten neu streichen, wie in der Abbildung gezeigt. In diesem Fall bleibt die "schwarze Höhe" gleich, jedoch ist ein Verstoß gegen Regel 3 für Element G möglich, weshalb für diesen Knoten rekursiv ein weiterer Ausgleich aufgerufen werden muss.
Fall zwei - ein schwarzer Onkel - Vater und Großvater in verschiedene Richtungen.
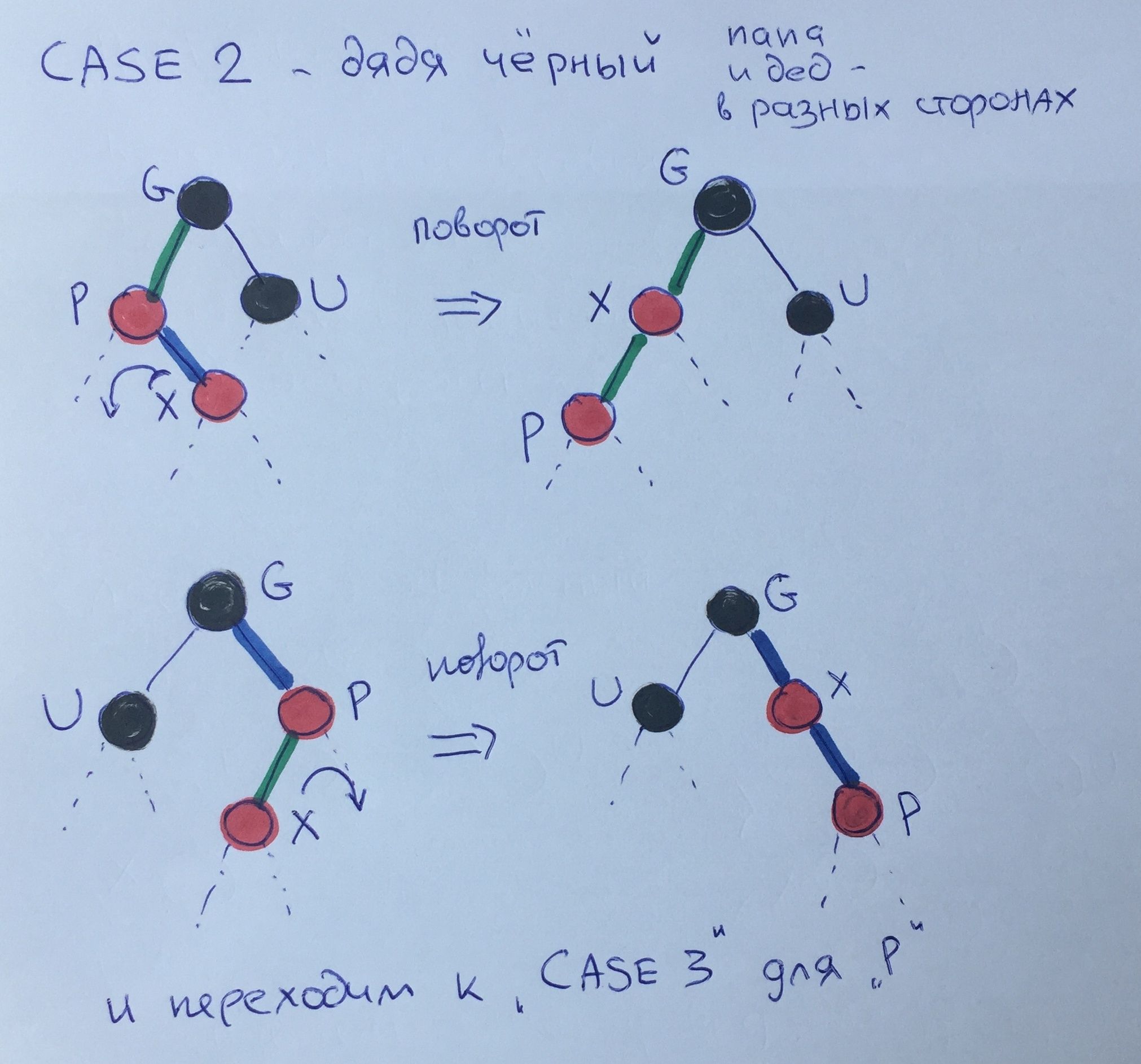
Diese Struktur muss zum dritten Fall gebracht werden, wenn Vater und Großvater in die gleiche Richtung gehen. Dazu müssen Sie eine kleine Runde von Sohn X zu seinem Vater machen (die Rundenregeln werden in diesem Artikel nicht berücksichtigt) und 3 Fälle für Element R aufrufen.
Fall drei - Schwarzer Onkel - Vater und Großvater auf derselben Seite
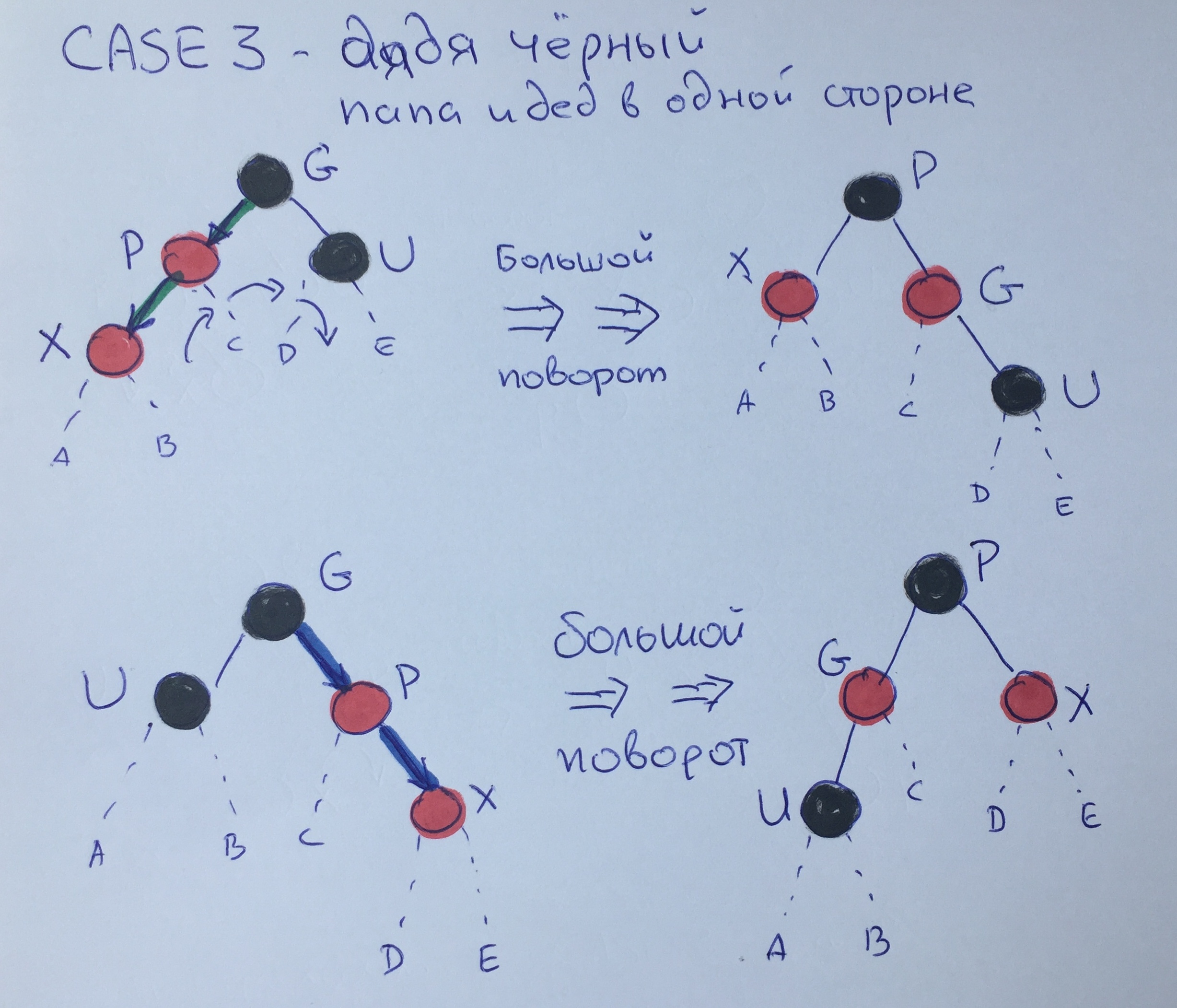
In diesem Fall können wir bereits eine große Wendung vom Vater über den Großvater zum schwarzen Onkel machen und P in Schwarz und G in Rot neu streichen. Infolge dieser Rotation wird die 3-Regel erfüllt.
Stellen Sie sicher, dass auch die 4. Regel erfüllt ist. Angenommen, vor der großen Kurve betrug die schwarze Höhe des Elements G N + 2. Dann ist die Höhe der "hängenden" Elemente wie folgt:
A = N + 1,
B = N + 1,
C = N + 1,
D = N.
E = N.
Überzeugen Sie sich selbst, dass nach dem Drehen die 4-Regel für alle Elemente gilt.
Konkretes Beispiel
Nun betrachten wir den Prozess der Bildung eines rot-schwarzen Baums mit sequentieller Einfügung der Elemente 1, 2, 3, 4, 5 und 6.
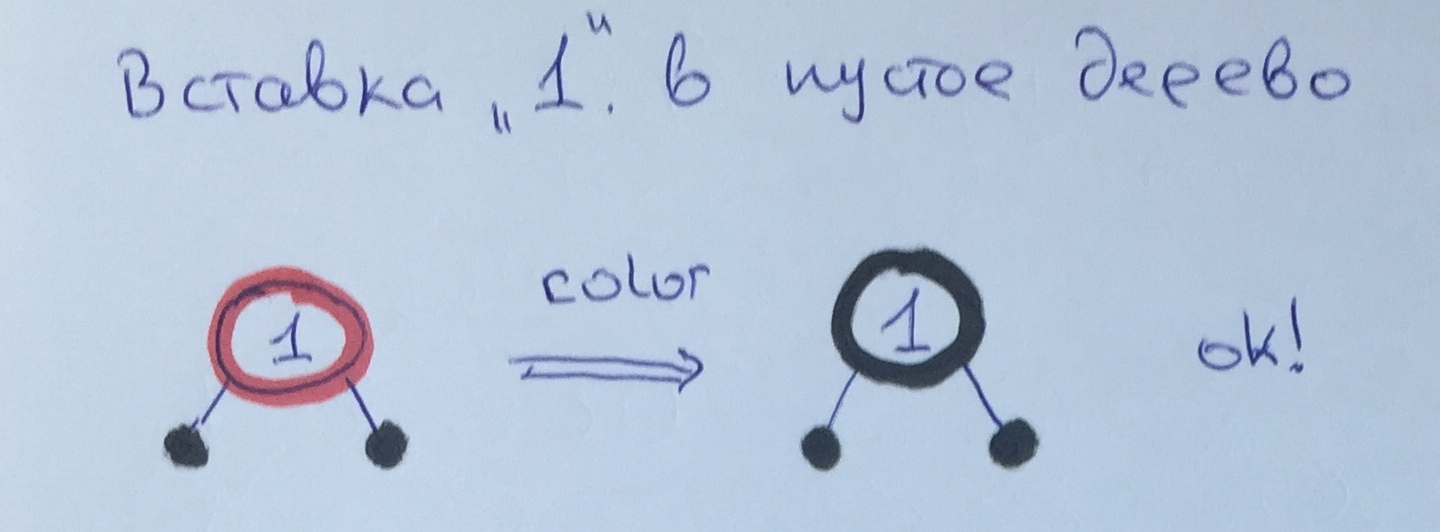
Da Element 1 die Wurzel ist, streichen wir es einfach neu, um Regel 1 zu erfüllen.
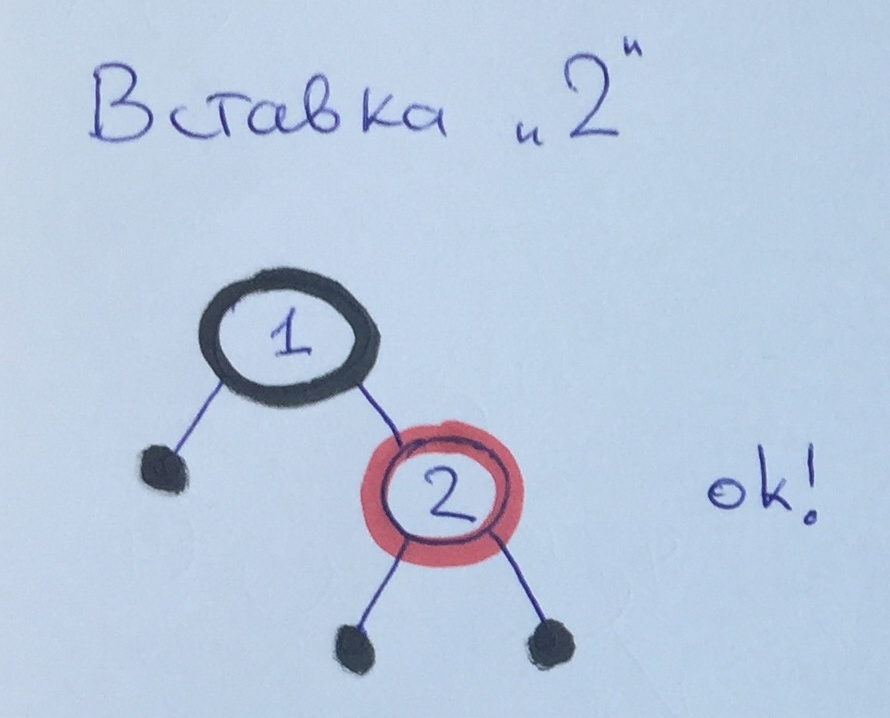
Nach dem Hinzufügen von Element 2 werden alle Regeln ausgeführt.
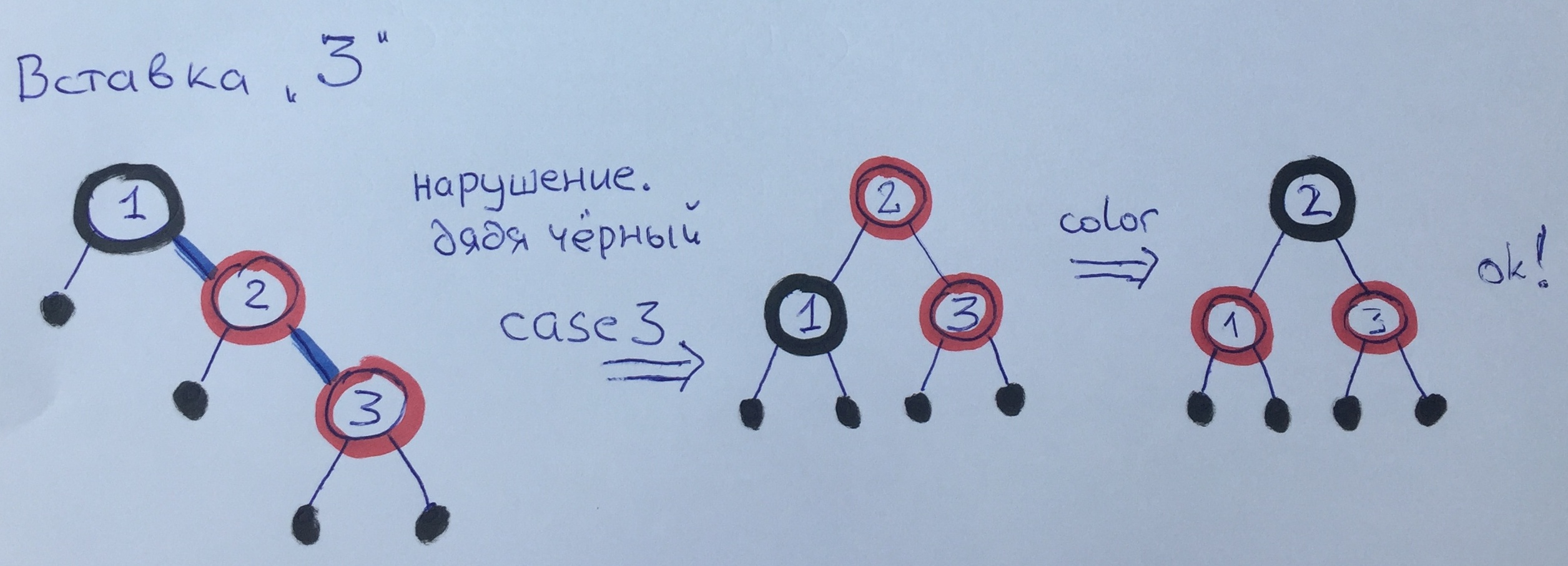
Beim Hinzufügen von Element 3 haben wir Regel 3 verletzt. Da wir einen schwarzen Onkel und einerseits Großvater und Vater haben, verwenden wir den dritten Fall - wir drehen uns um und streichen neu.
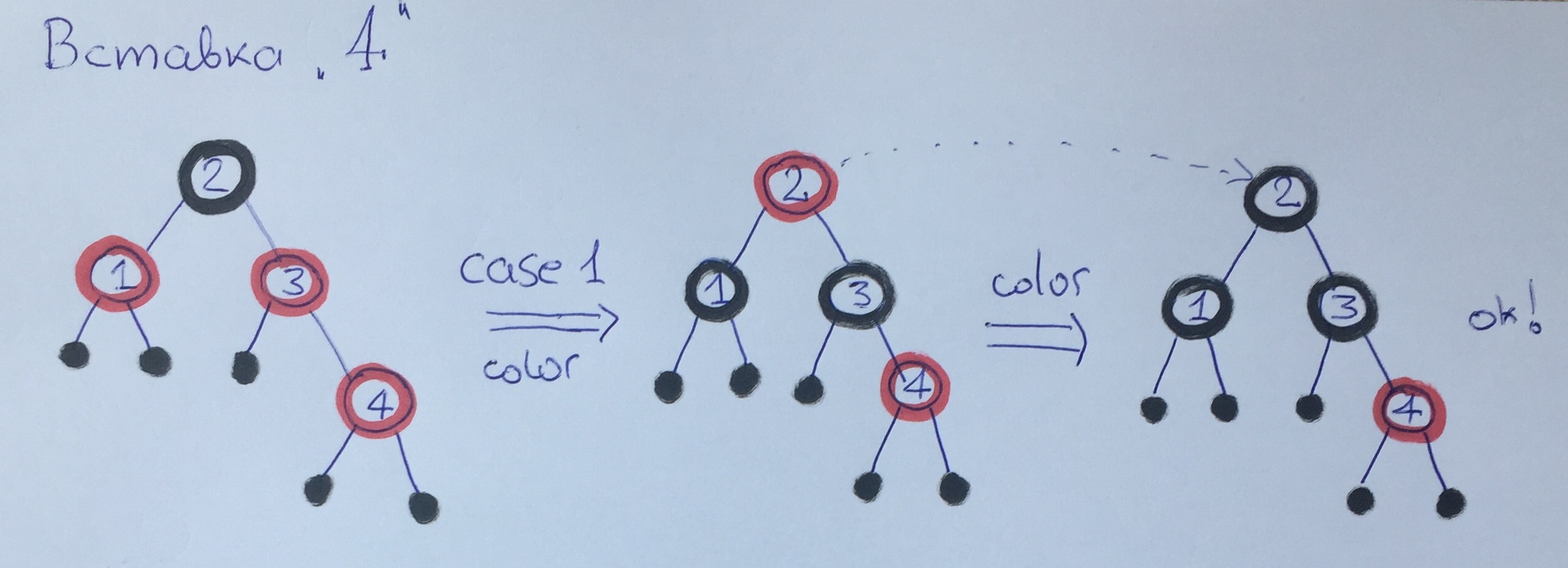
Beim Hinzufügen von Element 4 haben wir erneut gegen Regel 3 verstoßen. Diesmal ist unser Onkel rot, daher wenden wir den ersten Fall mit Neulackierung an - die schwarze Höhe des Baumes erhöht sich um 1. Bitte beachten Sie. dass der Ausgleichsalgorithmus zusätzlich für das Großvaterelement 2 gestartet wird, das wie die Wurzel einfach in schwarz neu gestrichen wird.
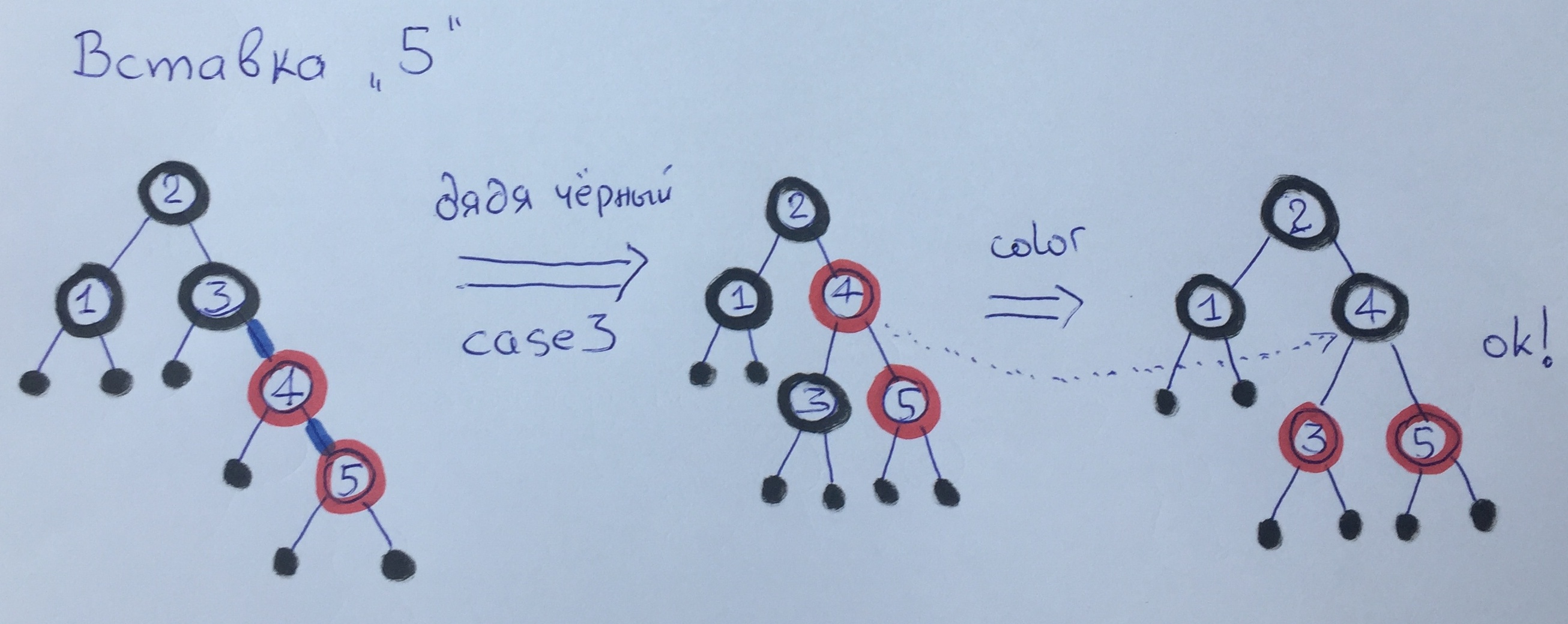
Beim Einfügen von Element 5 wenden wir erneut den Fall 3 an - wir machen eine große Kurve und streichen die Eckpunkte neu. Beachten Sie, dass sich die schwarze Höhe nicht geändert hat.
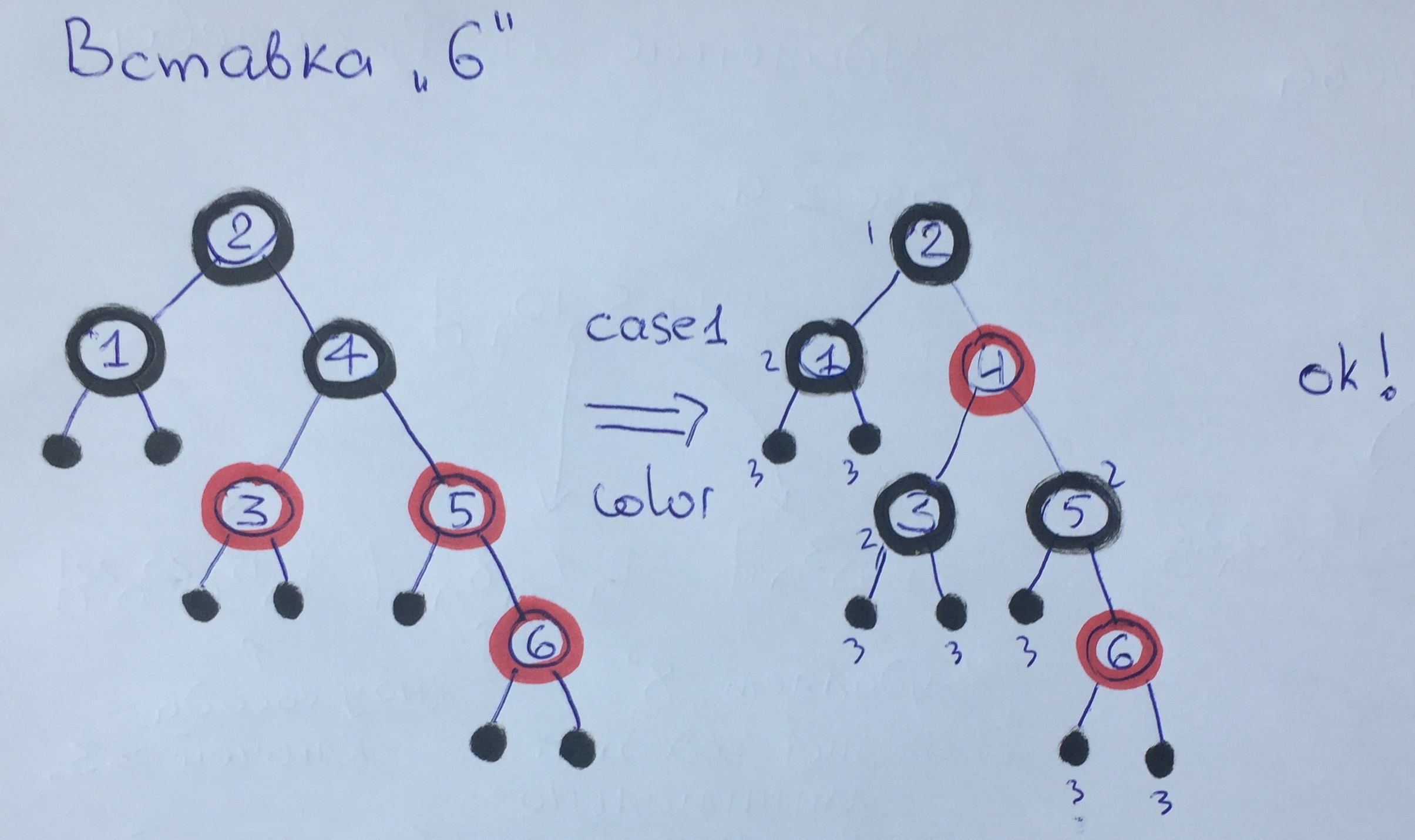
Beim Hinzufügen von Element 6 haben wir erneut gegen Regel 3 verstoßen. Da unser Onkel rot ist, wenden wir den ersten Fall mit Neulackierung an, die schwarze Höhe hat sich nicht geändert. Der Ausgleichsaufruf für 4 Elemente hat nichts im Baum geändert, da dieses Element nicht gegen die Regeln verstößt.
Daher haben wir uns mit den Problemen des Ausgleichs von Rot-Schwarz-Bäumen vertraut gemacht, detaillierter und mit Beispielen für Algorithmen in diesem Thema sowie mit verschiedenen anderen binären Suchbäumen, die wir im Kurs
"Algorithmen für Entwickler" betrachten .