Stochastischer Gradientenabstieg (SGD) für die logarithmische Verlustfunktion (LogLoss) in einem binären Klassifizierungsproblem

Der vorherige Teil (über lineare Regression, Gradientenabstieg und wie alles funktioniert) - habr.com/en/post/471458

In diesem Artikel werde ich zuerst die Lösung des Klassifizierungsproblems zeigen, wie sie sagen, "Stifte", ohne Bibliotheken von Drittanbietern für SGD, LogLoss und Berechnen von Verläufen, und dann die PyTorch-Bibliothek verwenden.

Ziel: Bestimmen Sie für zwei kategoriale Merkmale, die Gelbfärbung und Symmetrie beschreiben, zu welcher Klasse (Apfel oder Birne) das Objekt gehört (lehren Sie das Modell, Objekte zu klassifizieren).

Laden Sie zunächst unseren Datensatz hoch:

import pandas as pd data = pd.read_csv("https://raw.githubusercontent.com/DLSchool/dlschool_old/master/materials/homeworks/hw04/data/apples_pears.csv") data.head(10) 

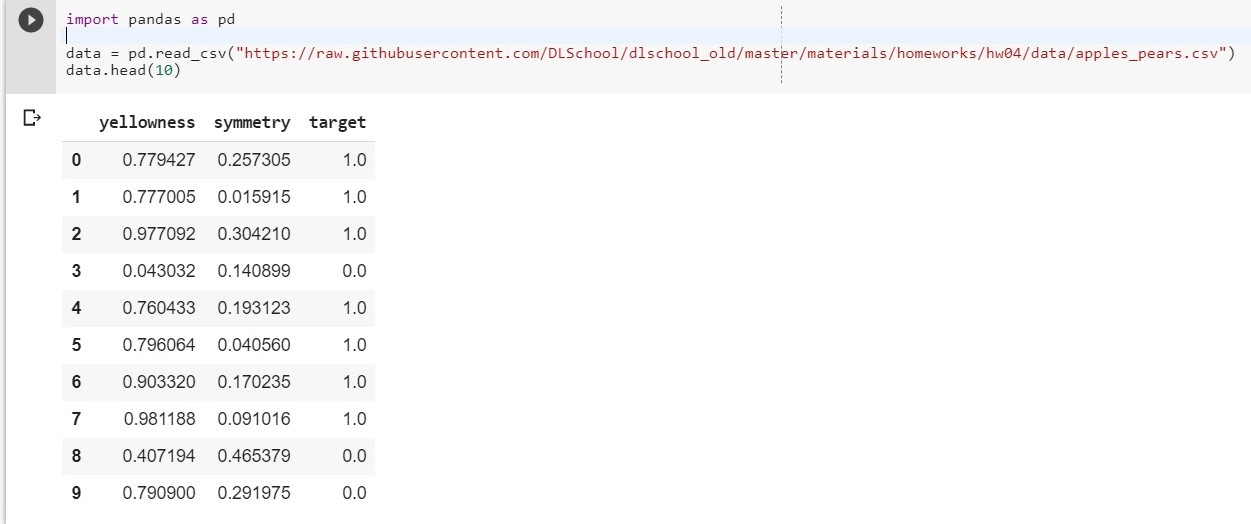
Sei: x1 - Gelbfärbung, x2 - Symmetrie, y = Ziel

Wir setzen die Funktion y = w1 * x1 + w2 * x2 + w0 zusammen
(w0 wird als Vorspannung betrachtet (dt. - Vorspannung))

Unsere Aufgabe beschränkt sich nun darauf, die Gewichte w1, w2 und w0 zu finden, die die Abhängigkeit von y von x1 und x2 am genauesten beschreiben.

Wir verwenden die logarithmische Verlustfunktion:



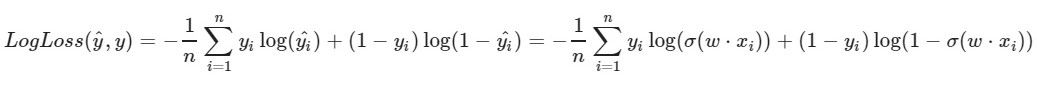
Der linke Parameter der Funktion ist die Vorhersage mit den aktuellen Gewichten w1, w2, w0

Der richtige Parameter der Funktion ist der richtige Wert (Klasse ist 0 oder 1)

σ (x) ist die Sigmoidaktivierungsfunktion von x

log (x) - der natürliche Logarithmus von x

Es ist klar, dass je kleiner der Wert der Verlustfunktion ist, desto besser haben wir die Gewichte w1, w2, w0 gewählt. Wählen Sie dazu einen stochastischen Gradientenabstieg .

Ich stelle fest, dass die Formel für LogLoss angesichts der Tatsache, dass wir in SGD ein Element und nicht eine gesamte Auswahl (oder eine Teilstichprobe, wie im Fall eines Mini-Batch-Gradientenabstiegs) auswählen, anders aussehen wird:


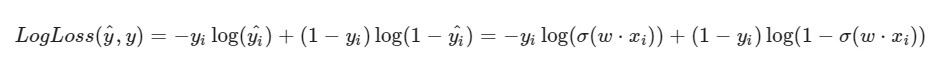Lösungsfortschritt:

Die Anfangsgewichte w1, w2, w0 erhalten zufällige Werte

Wir nehmen ein i-tes Objekt unseres Datensatzes (zum Beispiel zufällig), berechnen LogLoss dafür (mit unseren w1, w2 und w0, denen wir anfänglich zufällige Werte zugewiesen haben), dann berechnen wir die partiellen Ableitungen für jedes der Gewichte w1, w2 und w0, Aktualisieren Sie dann jedes der Gewichte.

Eine kleine Vorbereitung:

 import pandas as pd import numpy as np X = data.iloc[:,:2].values #  - y = data['target'].values.reshape((-1, 1)) #  (    ) x1 = X[:, 0] x2 = X[:, 1] def sigmoid(x): return 1 / (1 + np.exp(-x)) 

Implementierung:

 import random np.random.seed(62) w1 = np.random.randn(1) w2 = np.random.randn(1) w0 = np.random.randn(1) print(w1, w2, w0) # form range 0..999 idx = np.arange(1000) # random shuffling np.random.shuffle(idx) x1, x2, y = x1[idx], x2[idx], y[idx] # learning rate lr = 0.001 # number of epochs n_epochs = 10000 for epoch in range(n_epochs): i = random.randint(0, 999) yhat = w1 * x1[i] + w2 * x2[i] + w0 w1_grad = -((y[i] - sigmoid(yhat)) * x1[i]) w2_grad = -((y[i] - sigmoid(yhat)) * x2[i]) w0_grad = -(y[i] - sigmoid(yhat)) w1 -= lr * w1_grad w2 -= lr * w2_grad w0 -= lr * w0_grad print(w1, w2, w0) 

[0.49671415] [-0.1382643] [0.64768854]
[0.87991625] [-1.14098372] [0.22355905]

* _grad ist die Ableitung des entsprechenden Gewichts. Ich werde die allgemeine Formel schreiben:



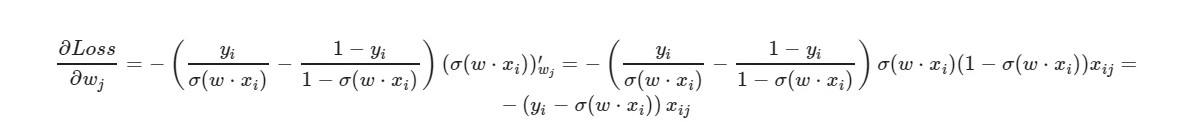
Für den freien Term w0 wird der Faktor x weggelassen (gleich eins angenommen).

Anhand der endgültigen Formel der Ableitung können wir erkennen, dass wir die Verlustfunktion nicht explizit berechnen müssen (wir benötigen nur partielle Ableitungen).

Lassen Sie uns überprüfen, wie viele Objekte aus dem Trainingssatz unser Modell die richtigen Antworten gibt und wie viele - die falschen.

 i = 0 correct = 0 incorrect = 0 for item in y: if(np.around(x1[i] * w1 + x2[i] * w2 + w0) == item): correct += 1 else: incorrect += 1 i = i + 1 print(correct, incorrect) 

925 75

np.around (x) - rundet den Wert von x. Für uns: Wenn x> 0,5, dann ist der Wert 1. Wenn x ≤ 0,5, dann ist der Wert 0.

Und was machen wir, wenn die Anzahl der Merkmale des Objekts 5 beträgt? 10? 100? Und wir werden die entsprechende Menge an Gewichten haben (plus eins für Voreingenommenheit). Es ist klar, dass es unpraktisch ist, manuell mit jedem Gewicht zu arbeiten und Gradienten dafür zu berechnen.

Wir werden die beliebte PyTorch-Bibliothek verwenden.

PyTorch = NumPy + CUDA + Autograd (automatische Berechnung von Gradienten)

PyTorch-Implementierung:

 import torch import numpy as np from torch.nn import Linear, Sigmoid def make_train_step(model, loss_fn, optimizer): def train_step(x, y): model.train() yhat = model(x) loss = loss_fn(yhat, y) loss.backward() optimizer.step() optimizer.zero_grad() return loss.item() return train_step X = torch.FloatTensor(data.iloc[:,:2].values) y = torch.FloatTensor(data['target'].values.reshape((-1, 1))) from torch import optim, nn neuron = torch.nn.Sequential( Linear(2, out_features=1), Sigmoid() ) print(neuron.state_dict()) lr = 0.1 n_epochs = 10000 loss_fn = nn.MSELoss(reduction="mean") optimizer = optim.SGD(neuron.parameters(), lr=lr) train_step = make_train_step(neuron, loss_fn, optimizer) for epoch in range(n_epochs): loss = train_step(X, y) print(neuron.state_dict()) print(loss) 

OrderedDict ([('0.weight', Tensor ([[- 0.4148, -0.5838]])), ('0.bias', Tensor ([0.5448])])
OrderedDict ([('0.weight', Tensor ([[5.4915, -8.2156]])), ('0.bias', Tensor ([- 1.1130])]])
0,03930133953690529

Ziemlich guter Verlust an der Testprobe.

Hier wird MSELoss als Verlustfunktion ausgewählt.

Mehr zu Linear

Kurz gesagt: Wir geben dem Eingang 2 Parameter (unsere x1 und x2 wie im vorherigen Beispiel) und wir erhalten einen Parameter (y) zum Ausgang, der wiederum dem Eingang der Aktivierungsfunktion zugeführt wird. Und dann sind sie bereits berechnet: der Wert der Fehlerfunktion, Gradienten. Am Ende werden die Gewichte aktualisiert.

Im Artikel verwendete Materialien