Nach Verteilung sortieren

Bei Verteilungssortierungen werden Elemente verteilt und in Klassen neu verteilt, bis das Array sortiert ist.

Im allgemeinsten Fall geschieht dies ungefähr auf die gleiche Weise. Elemente werden nach einem bestimmten Kriterium nach Klassen gestreut. Wenn dies nicht zur Reihenfolge des Arrays führt, werden die Attribute der Klasse verfeinert und die Elemente erneut auf die verfeinerten Klassen verteilt. Und dies geschieht, bis das Array geordnet wird.

Bei der Sortierung nach Verteilung gibt es fast immer keine Vergleiche von Elementen untereinander und deren Austausch. Die Hauptsache ist, ob das Element zu einer bestimmten Klasse gehört oder nicht, sein Vergleich mit anderen Elementen spielt selten eine Rolle.

Typischerweise weisen diese Sortierungen eine lineare Zeitkomplexität auf (und nicht logarithmisch, wie bei effizienten Arten von Austauschen, Zusammenführen, Auswählen oder Einfügen). Außerdem benötigen die Algorithmen dieser Klasse fast immer viel zusätzlichen Speicher, da die nach Klassen gruppierten Elemente irgendwo gespeichert werden müssen.

Verteilungssortierungen eignen sich zum Sortieren von Ganzzahlen und Zeichenfolgen. Das Sortieren von reellen Zahlen mit ihnen ist normalerweise unpraktisch. Außerdem sortiert die Verteilung Arrays, die aus sich wiederholenden Zahlen bestehen, perfekt - je mehr Wiederholungen, desto weniger unterschiedliche Klassen sind erforderlich.

Dieser Artikel wurde mit Unterstützung von EDISON verfasst.
Kundenmeinung : 10 Pluspunkte Programmierer von EDISON
Das ist interessant und nützlich zu wissen: Frühstücksprogrammierer

Stellen Sie sich einen Algorithmus vor, der die oben genannten Eigenschaften am konvexsten demonstriert.

Eimersortierung :: Eimersortierung

Andere Namen sind Korbsortierung, Blocksortierung, Taschensortierung.

Wir streuen Zahlen in Körbe, dann in jeden Korb in kleinere Körbe und so weiter, bis auf einer bestimmten Ebene im Korb nur noch dieselben Elemente vorhanden sind. Dann ist es aus solchen Körben der niedrigsten Ebene einfach, das Array in einem geordneten Zustand wiederherzustellen.

Lassen Sie uns anhand eines konkreten Beispiels erklären. Nehmen wir an, wir haben ein ungeordnetes Array. Es ist bekannt, dass dieses Array Zahlen von 1 bis 8 enthält.



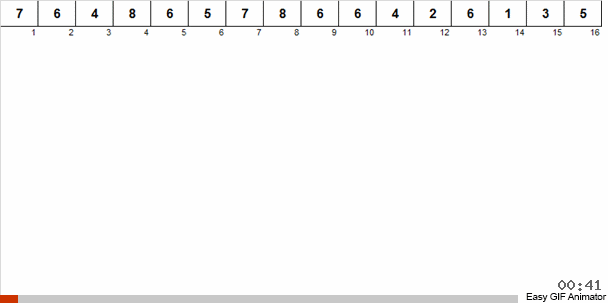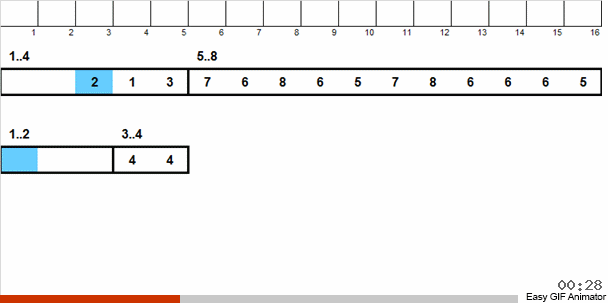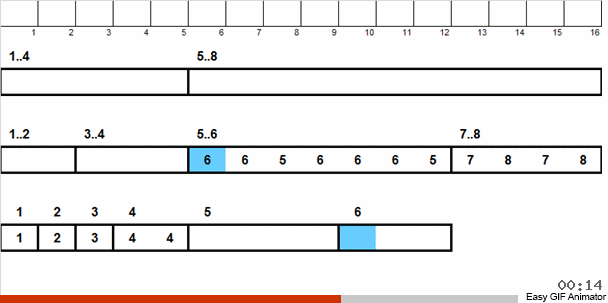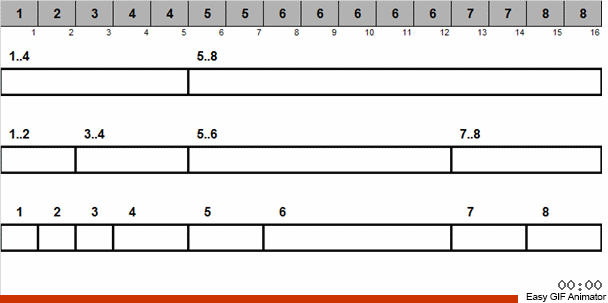
Wir werfen diese Zahlen in zwei Gruppen: Zahlen von 1 bis 4 fallen in eine Gruppe, von 5 bis 8 in die zweite. Dann verteilen wir die Zahlen im ersten Korb auf zwei Körbe: in eine Nummer 1 und 2 und in die anderen 3 und 4. Wir verteilen diese Körbe auch in Bastkörbe, die bereits gleich große Nummern enthalten. Auf diesen großen Korb mit Zahlen von 5 bis 8 wenden wir eine ähnliche Rekursion an.

Dann geben wir aus kleinen Körben, von denen jeder die gleichen Zahlen enthält, die Elemente in der Reihenfolge ihrer Priorität an das Hauptarray zurück.

Die nukleare Sortierung in dieser Form ist in der Praxis nicht besonders anwendbar, zeigt jedoch standardmäßig, wie alle Sortierungen nach Verteilung im Allgemeinen funktionieren.

Thanos sort :: Thanos sort

Manchmal werden mir Autorensorten geschickt, und das ist genau so. Der Autor Andrei Danilin nannte es "russische Sortierung in Hälften", aber ich nannte es die Sortierung von Thanos. Wenn wir formal von den verwendeten Methoden ausgehen, können wir die arithmetische mittlere Sortierung nennen.



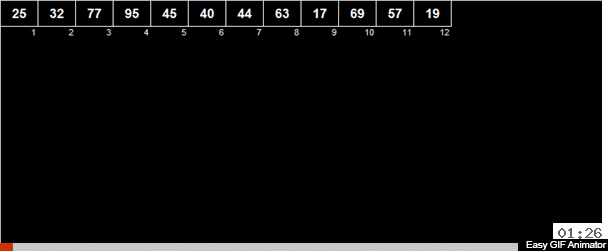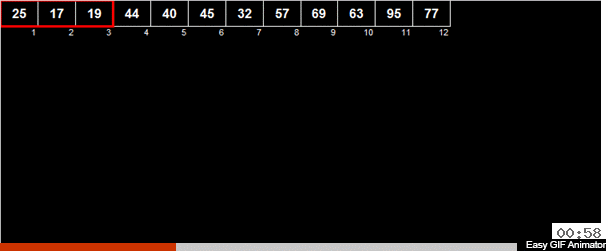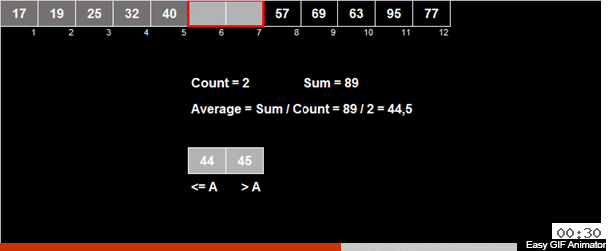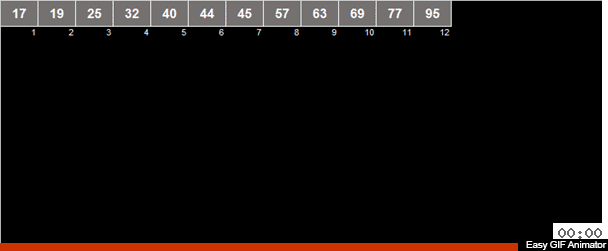
Das arithmetische Mittel der Elemente wird im Array berechnet und dann werden alle Elemente in 2 Gruppen verteilt. Elemente, die kleiner als (oder gleich) dem arithmetischen Mittel sind, gehen an eine Gruppe, größer als das arithmetische Mittel an die zweite Gruppe. Dann werden dieselben Aktionen rekursiv auf beide Gruppen angewendet - und so weiter bis zum bitteren Ende.

Und was ist mit verrücktem Titan? Wenn dies ein zufälliges Array ist, hat das Element im Vergleich zum arithmetischen Mittel im Großen und Ganzen eine 50/50-Chance, dass es in eine von zwei Gruppen geht.

Im Internet bin ich übrigens auf einen anderen Comic-Algorithmus mit demselben Namen gestoßen. Wenn das Array nicht sortiert ist, klicken Sie auf den Infinity-Handschuh und senden Sie die zufällig ausgewählte Hälfte der Array-Elemente an Nichtexistenz. Wenn die Überlebenden eine geordnete Gruppe bilden, kann ihre große Mission als erfüllt betrachtet werden. Wenn nicht bereits, können Sie noch ein paar Klicks machen.



Aber zurück zu unseren Verteilungssortierungen. Alle können in nur zwei Gruppen unterteilt werden - Sortieren und bitweise Sortieren . Wenn Sie möchten, können Sie auch Zählbit-Sortierungen hervorheben , d. H. diejenigen, die beiden zugeschrieben werden können.

Es gibt auch hybride Algorithmen (solche, die Methoden verschiedener Klassen verwenden, z. B. Tims Sortierung ist eine Kreuzung zwischen Zusammenführungssortierung und Einfügungssortierung, introspektive Sortierung ist eine schnelle Sortierung, die in eine Bündelsortierung usw. geht), einschließlich Verteilungssortierungen Hybriden sind jedoch ein separater Abschnitt. Über sie später.

Tausende Sortierungen und arithmetische Mittelsortierungen beziehen sich auf das Zählen von Sortierungen.

Sorten zählen

Die Grundidee ist, dass wir zählen, wie viele Zahlen in jeder Klasse sind.

Zählsortierung :: Zählsortierung

Wir zählen, wie oft die eine oder andere Zahl im Array vorkommt. Wenn wir diese Mengen kennen, bilden wir schnell ein bereits geordnetes Array.



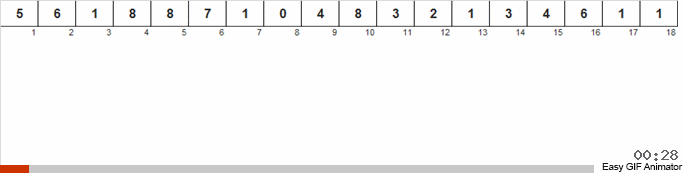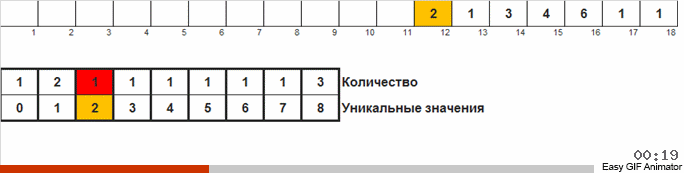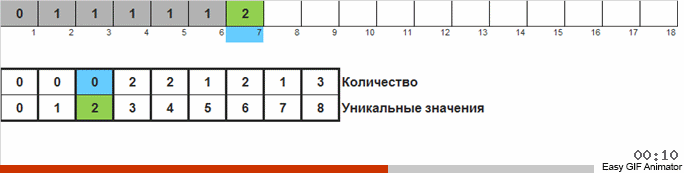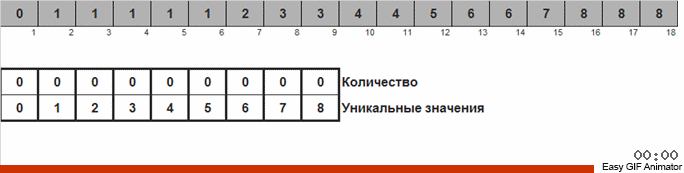
Für diese Sortierung müssen Sie das Minimum und Maximum im Array kennen. Dann werden die Schlüssel für das Hilfsarray generiert, in dem wir festlegen, was und wie oft es getroffen wurde.

Python-Code:

def CountingSort(array, mn, mx): count = defaultdict(int) for i in array: count[i] += 1 result = [] for j in range(mn,mx+1): result += [j]* count[j] return result 

Pigeon Sort :: Pigeonhole sort

Wir gehen durch das Array, wenn eine neue Nummer gefunden wird, dann starten wir den Zähler (als Schlüssel der Hilfsliste) dieser Nummer. Wenn die Nummer nicht zum ersten Mal gefunden wird, wird das Inkrement für diesen Zähler einfach ausgelöst.



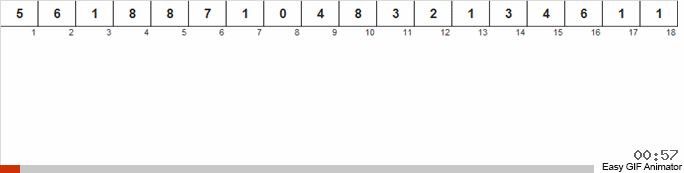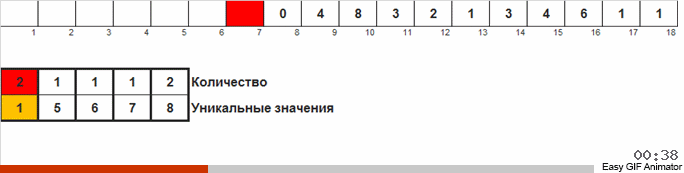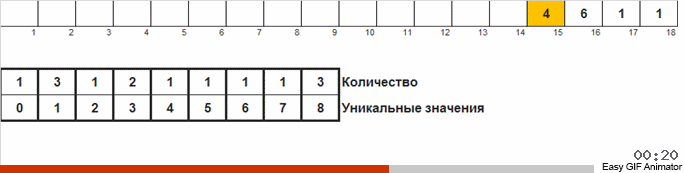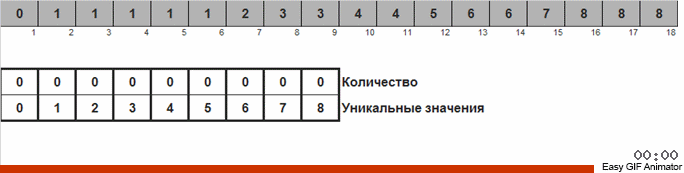
Der Unterschied zur vorherigen Methode besteht darin, dass wir beim Sortieren durch Zählen sofort Zähler für alle möglichen Zahlen starten, die im Array auftreten können (wir können es uns leisten, wenn das Maximum und das Minimum im Array bekannt sind). Einige Zahlen erscheinen nie und ihre Zähler zeigen Null. Bei der Taubensortierung starten wir Zähler nur für die Zahlen, die tatsächlich im Array vorkommen. Bei der Zählsortierung für Zähler wird ein Array verwendet, und bei der Taubensortierung wird eine doppelt verknüpfte Liste verwendet, mit der Sie unterwegs neue Zähler hinzufügen können.

Diese Methode wird manchmal alternativ als Dirichlet-Sortierung bezeichnet , da der Algorithmus selbst verschiedene Konsequenzen des Dirichlet-Prinzips veranschaulicht.

Wenn N Objekte auf M Container verteilt sind und N> M, enthält mindestens ein Container mehr als ein Element.

Python-Code:

 def PigeOnHoleSort(a): mi = min(a) size = max(a) - mi + 1 holes = [0] * size for x in a: holes[x - mi] += 1 i = 0 for count in range(size): while holes[count] > 0: holes[count] -= 1 a[i] = count + mi i += 1 

Bitsortierung

Wir verteilen die Nummern abhängig davon, welche Ziffer in einer bestimmten Kategorie der Nummer enthalten ist. Wenn wir dies mehrmals für verschiedene Ziffern tun, erhalten wir plötzlich ein sortiertes Array.

Bitweise Sortierung niedriger Ordnung :: LSD-Radix-Sortierung

Wir wechseln von den unteren zu den älteren Ziffern und verteilen bei jeder Iteration die Elemente des Arrays, je nachdem, welche Ziffer in der Ziffer enthalten ist.

Nach der nächsten Verteilung geben wir die Elemente in der Reihenfolge an das Hauptarray zurück, in der die Elemente bei der nächsten Umverteilung in die Klassen fielen.

Für bitweise Sortierungen ist es wichtig, dass Elemente die gleiche Anzahl von Ziffern haben. Wenn die tatsächliche Anzahl der Ziffern unterschiedlich ist, wird das Problem gelöst, indem zusätzliche Nullen als höhere Ziffern hinzugefügt werden.

Bitweise Sortierung höherer Ordnung :: MSD-Radix-Sortierung

Erstens verteilen wir uns auf die höheren Ränge, von denen wir zu den jüngeren wechseln.

Diese Option ist schwieriger zu implementieren, da der Übergang zu den unteren Ziffern innerhalb der Klassen und nicht unter allen Elementen des Arrays rekursiv durchgeführt wird.

Diese Komplexität wird jedoch durch die Tatsache belohnt, dass MSD schneller als LSD ist. Wenn Sie von den unteren zu den älteren Ziffern wechseln, müssen Sie alle Ziffern aller Zahlen verarbeiten, um richtig zu sortieren. Wenn Sie von älter zu jünger wechseln, müssen Sie tatsächlich nicht alle Ziffern aller Zahlen verarbeiten. Der sortierte Status kommt in der Regel früher.

Die meisten bitweisen Sortierungen sind eine Variation der effizienteren MSD. Dies ist besonders nützlich zum Sortieren von Zeichenfolgen. Hierzu wird normalerweise ein Suffixbaum verwendet. Wir werden in einem der folgenden Artikel analysieren.

Bitweise Sortierung zählen

Manchmal ist die Verteilungssortierung gleichzeitig zählbar und bitweise.

Perlensortierung :: Perlensortierung

Andere Namen des Algorithmus: Abakussortierung, Schwerkraftsortierung.

Ich habe bereits einige Male über diese Sortierung geschrieben ( 1 , 2 ), daher werde ich mich kurz fassen, nur die Essenz.

Angenommen, jede Zahl in einem Array ist eine Reihe von Kugeln, die Anzahl der Kugeln ist der Wert einer Zahl. Wenn wir die Zahlen als horizontale Reihen dieser Kugeln aufeinander anordnen und sie dann ganz vertikal verschieben, erhalten wir ein geordnetes Array.

Der Trick dabei ist, dass wir jede Zahl mit Bällen in einem unären Zahlensystem darstellen. Tatsächlich zählen wir einfach, wie oft alle Zahlen jede Ziffer haben.

BeadSort in Python in einer Zeile:

 #!/bin/python3 from itertools import zip_longest def beadsort(l): return list(map(sum, zip_longest(*[[1] * e for e in l], fillvalue=0))) 

Nach einer Weile werden wir komplexere zählbitweise Sortierungen analysieren, unter denen die Sortierung unter amerikanischer Flagge einen herausragenden Platz einnimmt.

Referenzen

Eimer / Eimer , Zählen / Pigeonhole / Dirichlet , Radix / Entladungen , Perle

Serienartikel:

• Excel-Anwendung AlgoLab.xlsm
• Sorte austauschen
• Insertion Sorts
• Nach Auswahl sortieren
• Sortierungen zusammenführen
• Nach Verteilung sortieren
  • Zählsorten mit ungefährer Verteilung
  • Amerikanische Flagge sortieren
  • Suffixbaum in bitweiser Sortierung
  • Vergleichen nach Sortierungen
• Hybridsortierung

Die AlgoLab Excel-Anwendung wurde erheblich aktualisiert. Einige Algorithmen aus dem heutigen Artikel erschienen dort zum ersten Mal. Aktualisieren Sie, wer verwendet.