Alles, was Sie über das Rückwärtspendel wissen wollten

Der Artikel dient als Spickzettel für diejenigen, die ihr umgekehrtes Pendel herstellen möchten. Hier sind die Probleme, aufgrund derer ich mehrmals überarbeitet habe. Ein kurzer Überblick über die Theorie ist erforderlich, um zu verstehen, wie das System stabilisiert werden kann.

Warum brauchte ich das?

Kurzum: Ich wollte meine CNC-Maschine erweitern, aber etwas ist schief gelaufen ...

Erfolglose Versuche

Das Projekt dauerte fast zwei Jahre des Versuchs und Irrtums, der Neugestaltung, des Wartens auf Details und unvollständiger freier Tage, so dass diejenigen, die es wiederholen möchten, Zeit und Nerven sparten. Ich halte es für notwendig, über erfolglose Entscheidungen zu sprechen.

• ein Gyroskop (MPU6050) anstelle eines Encoders - grundsätzlich nichts dagegen, aber der Sensor sollte sich auf einer rotierenden Stange befinden, dies führt zu einem unvorhersehbaren Effekt und der Unfähigkeit, die Stange mehrmals um die Achse zu rollen.
  
• Absolutwertgeber - Wenn es sich um ein Potentiometer handelt, führt selbst die Bewegung von Drähten (hauptsächlich aufgrund von Kontakten im Arduino) zu Rauschen bei den Messungen. Ein 10-Bit-ADC reicht immer noch nicht aus. Wenn es sich um einen teureren Sensor handelt, erfolgt das Lesen über eine serielle Schnittstelle, was zu einer Verzögerung des Systems führt, insbesondere in Kombination mit einem Schrittmotor.
  
• die Steifigkeit des Systems - irgendwann nahm ich ein Aluminiumrohr mit einer Last am Ende, als der Schlitten vibrierte, starke Vibrationen begannen und es nicht sofort klar war, welches System wir stabilisierten. Wir müssen uns bemühen, sicherzustellen, dass das physische System so nah wie möglich an dem ist, was modelliert wird.
  
• Reibung - dieses Phänomen wird oft vernachlässigt, ich habe versucht, es mit großen Wagenrädern und V-Schlitzprofilen zu reduzieren, im Gegensatz zu Schienen mit Schiebern mit kleinen Kugeln, weil Die Rollreibung ist umgekehrt proportional zum Radius.
  
• Die Verwendung eines Schrittmotors - Ich habe viel Zeit damit verbracht, diesen Weg zu gehen. Es ist irreführend, die Formeln (tatsächlich steuern wir sofort die Beschleunigung der Basis des Pendels) und die Einfachheit des Designs (wir können die Reibung in der Schiene, dem Motorgeber, vergessen, wenn wir davon ausgehen, dass der Motor keine Schritte überspringt) zu vereinfachen. , aber ... Um die Geschwindigkeit genau zu steuern, sollte die Zeit zwischen den Schritten einige zehn Mikrosekunden betragen. Dies bedeutet, dass Sie die Statusausgabe an die Konsole vergessen können. Ohne Rückmeldung können Sie nicht sicher sein, dass der Motor die Schritte nicht verpasst hat und die Geschwindigkeit wirklich dem entspricht, was das System denkt. Ich behaupte nicht, dass dies eine Sackgasse ist. Wenn es jemandem gelingt, das Pendel mit einem Schrittmotor zu stabilisieren, werde ich es mir gerne ansehen.
  

Freies Pendel

Um das Bild zu vervollständigen, simulieren wir ein Pendel auf einem freien Wagen ohne Reibung.

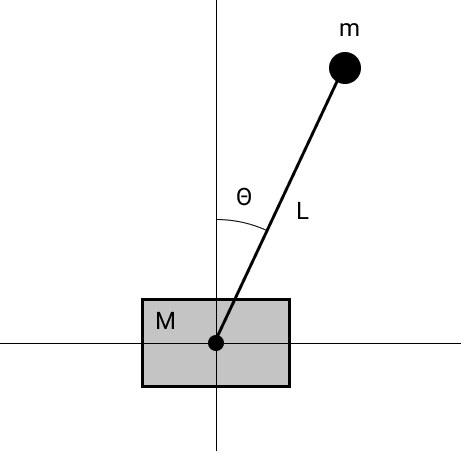
Die Bewegungsgleichungen können erhalten werden, indem der Lagrange in Bezug auf verallgemeinerte Koordinaten differenziert wird. Wir erhalten die folgenden Gleichungen:

$$

$$\ begin {Fälle} L \ cdot \ ddot \ theta + g \ cdot {sin (\ theta)} - \ ddot {x} \ cdot {cos (th)} = 0 \\ (m + M) \ cdot \ ddot {x} + m \ cdot \ ddot {\ theta} \ cdot {L} \ cdot {cos (\ theta)} - m \ cdot {L} \ dot {\ theta} ^ 2 \ cdot {sin (\ theta )} = 0 \ end {case}$$

Hier können Sie feststellen, wie sich der Zustandsvektor ändert:

$$

$$\ begin {case} \ dot \ theta = w \\ \ dot {w} = \ frac {g \ cdot {sin (\ theta)} + b \ cdot {L} \ cdot {w ^ 2} \ cdot { sin (\ theta)} \ cdot {cos (\ theta)}} {L \ cdot (1 + b \ cdot {cos ^ 2 (\ theta))}} \\ \ dot {x} = v \\ \ dot {v} = b \ cdot \ frac {L \ cdot {w ^ 2} \ cdot {sin (\ theta)} - g \ cdot {sin (\ theta)} \ cdot {cos (\ theta)}} {1 + b \ cdot {cos ^ 2 (\ theta)}} \ end {case}, b = \ frac {m} {M + m}$$

und simulieren Sie das System. Der Code ist hier .

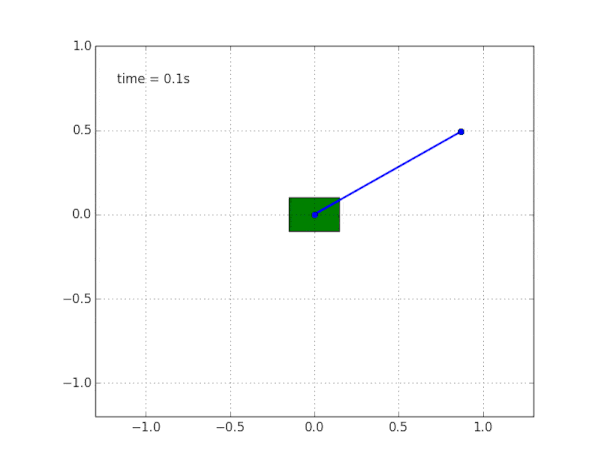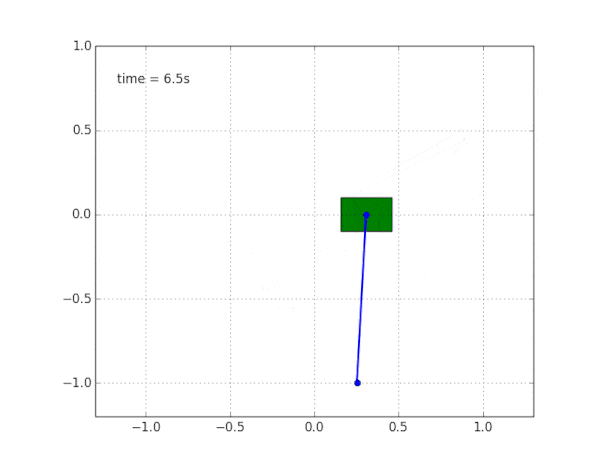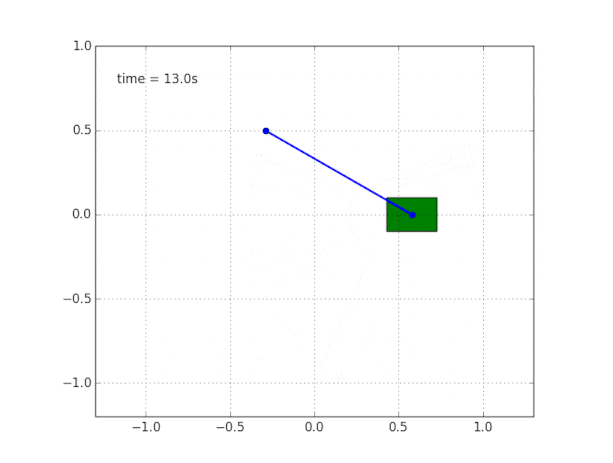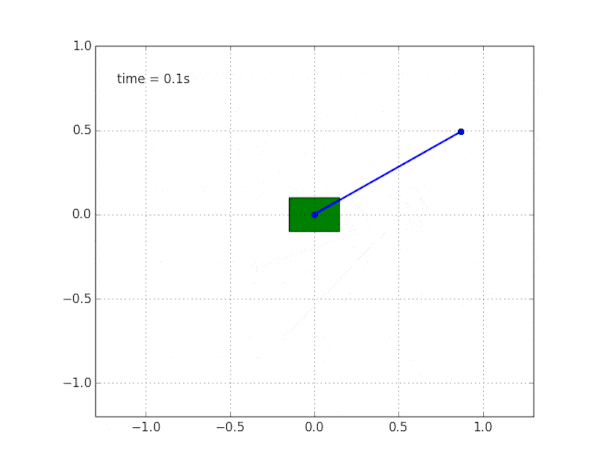
Warum ist das System instabil?

Der gesunde Menschenverstand und die Visualisierung sagen uns, dass das Pendel selbst nicht stehen wird. Aber wie kann man das mathematisch überprüfen?
Im Allgemeinen sind das linearisierte System und die Lösung wie folgt:

$$

$$\ dot {\ mathbf {x}} = A \ mathbf {x}, \ mathbf {x} (t) = e ^ {At} \ mathbf {x} (0)$$

Ein Exponent in der Potenz der Matrix sieht klarer aus, wenn wir von Eigenvektoren zum Koordinatensystem gehen, dann zur Matrix $$$A$ wird diagonal sein ( $$$D$ ), und der Aussteller sieht aus wie:

$$

$$e ^ {Dt} = \ begin {bmatrix} e ^ {\ lambda_1t} & 0 & \ dots & 0 \\ 0 & e ^ {\ lambda_2t} & \ dots & 0 \\ \ vdots & \ vdots & \ ddots & \ vdots \\ 0 & 0 & \ dots & e ^ {\ lambda_nt} \\ \ end {bmatrix}$$

Nun ist es in Gegenwart von Eigenwerten zu sehen ( $$$\ lambda_i$ ) Bei einem positiven Realteil tendiert die entsprechende Komponente des Zustandsvektors zur Unendlichkeit und das System fällt auseinander. Das Obige gilt für kontinuierliche Systeme. In dieser Videovorlesung wird mehr über Nachhaltigkeit beschrieben.
Überprüfen Sie, ob dies beim umgekehrten Pendel der Fall ist. Wir linearisieren unser System nahe der Gleichgewichtsposition für $$$\ theta = 0, sin (\ theta) \ ungefähr \ theta, cos (\ theta) \ ungefähr 1, w ^ 2 \ ungefähr 0$ ::

$$

$$\ begin {bmatrix} \ dot \ theta \\ \ dot \ omega \\ \ dot {x} \\ \ dot {v} \ end {bmatrix} = \ begin {bmatrix} 0 & 1 & 0 & 0 \\ \ frac {g} {L (1 + b)} {\ theta} & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ -g \ frac {b} {1 + b} \ theta & 0 & 0 & 0 \ end {bmatrix} \ begin {bmatrix} \ theta \\ \ omega \\ x \\ v \ end {bmatrix}$$

Nicht-Null-Eigenwerte haben die Form $$$\ pm \ sqrt {\ frac {g} {L (1 + b)}}$ So wurden wir von Instabilität überzeugt.

Feedback hinzufügen

Jetzt wirkt die Kraft auf den Wagen $$$f$ kann eine der Gleichungen in folgender Form umgeschrieben werden: $$$(m + M) \ cdot \ ddot {x} + m \ cdot \ ddot {\ theta} \ cdot {L} \ cdot {cos (\ theta)} - m \ cdot {L} \ dot {\ theta} ^ 2 \ cdot {sin (\ theta)} = f$ und das linearisierte System hat die Form:

$$

$$\ begin {bmatrix} \ dot \ theta \\ \ dot \ omega \\ \ dot {x} \\ \ dot {v} \ end {bmatrix} = \ begin {bmatrix} 0 & 1 & 0 & 0 \\ \ frac {g} {L (1 + b)} {\ theta} & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ -g \ frac {b} {1 + b} \ theta & 0 & 0 & 0 \ end {bmatrix} \ begin {bmatrix} \ theta \\ \ omega \\ x \\ v \ end {bmatrix} + \ begin {bmatrix} 0 \\ \ frac {1} {L} \ frac {1} {2m + M} \\ 0 \\ \ frac {1} {2m + M} \ end {bmatrix} \ cdot {f}$$

Nun das System ( $$$\ dot {\ mathbf {x}} = A \ mathbf {x} + Bu$ ) steuerbar wurde , kann dies überprüft werden, indem der Rang der Matrix überprüft wird $$$\ begin {bmatrix} B && AB && A ^ 2B && A ^ 3B \ end {bmatrix}$ gleich der Dimension des Zustandsvektors, d.h. 4. Um das Pendel aufrecht zu halten, habe ich einen linear-quadratischen Zustandsregler verwendet, d. H. Kontrolle (u oder f) ist das Produkt des Zustandsvektors $$$[\ theta, \ dot {\ theta}, x, \ dot {x}]$ durch einen Vektor von Parametern, die einmal durch Minimieren der quadratischen Funktion gefunden werden . Der Simulationscode ist hier .

Motorsteuerung

Jetzt müssen Sie den Gleichstrommotor steuern. Er enthält viele Parameter, die ich nicht kenne. Deshalb habe ich ihn für eine "Black Box" verwendet, die durch die folgenden Gleichungen unter Berücksichtigung der Reibung beschrieben wird:

$$

$$\ begin {Fälle} \ dot {x} = v \\ \ dot {v} = -a \ cdot {v} + b \ cdot {U} + c \ cdot {Zeichen (v)} \ end {Fälle}$$

Über die Ableitung von Gleichungen und die Parameterschätzung können Sie hier lesen. Im Folgenden gebe ich meine Diagramme der Beschleunigung des Motors mit dem Schlitten in Abhängigkeit von der Spannung (in Wirklichkeit wird das PWM-Signal von der Steuerung ausgegeben) und den angepassten Kurven.

Ich fand auch die Koeffizienten des Modells durch Brute Force, den Code .
Somit gibt uns die Steuerung die erforderliche Beschleunigung, und aus der zweiten Gleichung, die alle Konstanten kennt, finden wir die Spannung.

Das reale Gerät zusammenbauen

Jetzt haben wir alle Kenntnisse, um das Pendel zu sammeln und zu stabilisieren. Ich habe folgendes Eisen verwendet:

• Arduino Mega 2560 ist nicht UNO, da zwei Encoder 4 Pins für Interrupts benötigen
• Der Encoder für das Pendel - OMRON E6B2-CWZ6C 2500 Impulse pro Umdrehung - gibt uns den Winkel an, wir berechnen die Winkelgeschwindigkeit, die Auflösung ist ziemlich hoch, so dass es genügend endliche Differenzen ohne Glättung und Mittelung gab
• Der Encoder für den Motor - LPD3806-600BM-G5-24C 600 Impulse pro Umdrehung - gibt die Position des Wagens an, berechnet die Drehzahl
• 12V Gleichstrommotor mit 5: 1 Getriebe
• 10 Ampere 5V-30V Motortreiber

So messen wir explizit den Winkel des Pendels, die Position des Wagens, berechnen die Winkelgeschwindigkeit des Pendels und die Geschwindigkeit des Wagens - wir erhalten den vollen Zustand, ich habe die Reglerparameter mit diesem Skript gefunden. Überraschenderweise funktionierte alles schnell so wie es war. Ich bin mit dem Ergebnis zufrieden, es steht und hält sogar ein Glas!


Der Code für Arduino ist hier
Was könnte im Vergleich zu vielen Optionen auf Youtube verbessert werden? Dieses Pendel ist leise, da die PWM außerhalb des Hörbereichs eingestellt ist und Kunststoffräder verwendet werden.
Jetzt sieht diese Aufgabe wie eine Laborarbeit aus: die Parameter des Motors zu messen und die Koeffizienten des Reglers zu finden und gleichzeitig zu verstehen, was passiert.

Was weiter?

Ich habe vor, ein Pendel herzustellen: eine Schaukel machen, eine Drahtspule loswerden, eine Abschirmung mit praktischen Anschlüssen machen, damit es keine Schande ist, an eine Schule oder ein Museum zu spenden. Wenn jemand mitmachen möchte, bin ich froh, dass es noch viel ehrgeizigere Ideen gibt.

Referenzen

• Detaillierte Beschreibung des inversen Pendelproblems
• Wir kauen einen linear-quadratischen Regler, um ein umgekehrtes Pendel zu steuern - dieser Artikel hat mir beim Aufbau meines Pendels viel Zeit gespart
• Tolle TAU-Videovorträge

Vielen Dank für Ihre Aufmerksamkeit!