Das Gesetz der Beschleunigung der Rendite (Teil 1)

Hallo habr Ich präsentiere Ihnen die Übersetzung des Gesetzes zur Beschleunigung der Rückkehr von Raymond Kurzweil .

7. März 2001

Eine Analyse der Technologiegeschichte zeigt, dass die Anzahl der technologischen Veränderungen exponentiell zunimmt, obwohl die Entwicklung unter dem Gesichtspunkt des „gesunden Menschenverstandes“ intuitiv linear zu sein scheint. Das heißt, die Entwicklung über 100 Kalenderjahre des 21. Jahrhunderts wird ungefähr 20.000 Jahren Entwicklung in ihrem gegenwärtigen Tempo entsprechen. Die Effizienz oder Fortschrittsergebnisse wie Chipgeschwindigkeit oder Preis-Leistungs-Verhältnis nehmen ebenfalls exponentiell zu. Manchmal wächst sogar die exponentielle Wachstumsrate selbst exponentiell. Für mehrere Jahrzehnte wird die maschinelle Intelligenz die menschliche Intelligenz übertreffen und zur Singularität führen - technologische Veränderungen, die so schnell und tiefgreifend sind, dass sie das Gewebe der menschlichen Geschichte zerreißen. Zu den Konsequenzen gehört die Verschmelzung von biologischer und nicht-biologischer Intelligenz, unsterblichen Menschen, die in Form von Software existieren, und extrem hoher Intelligenz, die sich mit Lichtgeschwindigkeit durch das Universum bewegt.

Sie erhalten 40 Billionen US-Dollar, wenn Sie diesen Aufsatz lesen und verstehen, worum es geht. Siehe unten für weitere Details. (Ja, oft gehen die Autoren zu irgendwelchen Tricks, um Ihre Aufmerksamkeit zu erregen, aber ich meine diese Aussage absolut ernst. Bevor ich jedoch zur weiteren Erzählung zurückkehre, lesen Sie den ersten Satz dieses Absatzes sorgfältig durch.)

Kommen wir jetzt zurück in die Zukunft: Die meisten von uns verstehen das falsch. Unsere Vorfahren glaubten, dass die Zukunft ihrer Gegenwart sehr ähnlich sein würde, was wiederum ihrer Vergangenheit sehr ähnlich war. Obwohl es vor Tausenden von Jahren exponentielle Trends gab, befanden sie sich in einem sehr frühen Stadium, in dem der exponentielle Trend so flach ist, dass es nach einem Mangel an Trends aussieht. Somit waren ihre Annahmen größtenteils gerechtfertigt. Und heute erwartet jeder, geleitet von weltlicher Weisheit, einen allmählichen technologischen Fortschritt und die entsprechenden sozialen Konsequenzen. Die Zukunft wird jedoch viel überraschender sein, als die meisten Beobachter erkennen: Nur wenige von ihnen haben wirklich erkannt, dass sich die Geschwindigkeit des Wandels beschleunigt.

Intuitive lineare Ansicht versus historische Exponentialansicht

Die meisten langfristigen Vorhersagen über die technische Machbarkeit in zukünftigen Zeiträumen unterschätzen die Leistungsfähigkeit zukünftiger Technologien dramatisch, da sie auf einer von mir als "intuitiv linear" bezeichneten Sichtweise des technologischen Fortschritts und nicht auf einer "historisch-exponentiellen" Sichtweise beruhten. Mit anderen Worten, dies ist nicht der Fall, wenn man vom 21. Jahrhundert hundert Jahre Fortschritt erwarten sollte, sondern wir werden zwanzigtausend Jahre Fortschritt erleben (wenn wir Fortschritt in seinem gegenwärtigen Tempo meinen).

Diese Diskrepanz in den Perspektiven tritt häufig in verschiedenen Situationen auf, beispielsweise bei der Erörterung ethischer Fragen, die Bill Joy in seinem umstrittenen WIRED-Artikel „Warum wir die Zukunft nicht brauchen“ angesprochen hat. Bill und ich treffen uns oft bei verschiedenen Treffen und spielen die Rolle eines Optimisten bzw. eines Pessimisten. Und obwohl von mir erwartet wird, dass Kritiker von Bills Position kritisiert werden, und ich wirklich Fehler im von ihm vorgeschlagenen Konzept der „Ablehnung“ sehe, verteidige ich Joey letztendlich in der Regel in der Schlüsselfrage der Machbarkeit. Kürzlich wies einer der Redner, ein Nobelpreisträger, Bills Befürchtungen zurück und sagte: "Wir erwarten nicht, dass sich selbstreplizierende Nanoengineering-Objekte in weiteren hundert Jahren wiederfinden." Mir ist aufgefallen, dass 100 Jahre wirklich eine vernünftige Schätzung der Zeit sind, die der technologische Fortschritt benötigt, um dieses spezifische Ziel mit der heutigen Geschwindigkeit seiner Entwicklung zu erreichen. Da sich das Tempo des Fortschritts jedoch alle zehn Jahre verdoppelt, werden wir in nur 25 Kalenderjahren ein Jahrhundert Fortschritt mit der heutigen Geschwindigkeit erleben.

Wenn Menschen über die Zukunftsform nachdenken, gehen sie intuitiv davon aus, dass sich die derzeitige Geschwindigkeit des Fortschritts auch in Zukunft fortsetzen wird. Eine sorgfältige Überprüfung des Tempos der Technologieentwicklung zeigt jedoch, dass die Geschwindigkeit des Fortschritts nicht konstant ist und es die menschliche Natur ist, sich an ein sich änderndes Tempo so anzupassen, dass es intuitiv so aussieht, als würde das Tempo konstant bleiben. Selbst für diejenigen von uns, die lange genug gelebt haben, um zu spüren, wie sich das Tempo im Laufe der Zeit beschleunigt, erweckt unsere natürliche Intuition den Eindruck, dass der Fortschritt mit der gleichen Geschwindigkeit voranschreitet, wie wir uns in letzter Zeit gefühlt haben. Aus Sicht eines Mathematikers ist der Hauptgrund dafür, dass der Exponent in kurzen Abschnitten durch eine gerade Linie angenähert wird. Obwohl das Tempo des Fortschritts in der jüngsten Vergangenheit (zum Beispiel im letzten Jahr) viel höher war als vor zehn Jahren (ganz zu schweigen von vor hundert oder tausend Jahren), dominiert unsere jüngste Erfahrung die Erinnerungen. Daher ist es durchaus üblich, dass selbst anspruchsvolle Kommentatoren, die die Zukunft als Grundlage ihrer Erwartungen diskutieren, die aktuelle Änderungsrate für die nächsten 10 oder 100 Jahre extrapolieren. Deshalb nenne ich diese Art von Zukunftsaussichten eine „intuitiv lineare“ Sichtweise.

Eine ernsthafte Bewertung der Technologiegeschichte zeigt, dass der technologische Wandel exponentiell ist. Bei einem exponentiellen Wachstum stellen wir fest, dass ein Schlüsselindikator wie die Rechenleistung mit einem konstanten Koeffizienten für jede Zeiteinheit multipliziert wird (z. B. jedes Jahr verdoppelt) und nicht nur um einen bestimmten Betrag zunimmt. Exponentielles Wachstum ist ein charakteristisches Merkmal jedes Evolutionsprozesses, und die technologische Entwicklung kann als gutes Beispiel dienen.

Es ist möglich, Daten auf unterschiedliche Weise, in unterschiedlichen Zeitskalen und für eine breite Palette von Technologien, von elektronisch bis biologisch, auszuwerten, wobei die Beschleunigung des Fortschritts und seine Wachstumsrate beobachtet werden. Tatsächlich finden wir nicht nur exponentielles Wachstum, sondern auch "doppeltes" exponentielles Wachstum, dh die Rate des exponentiellen Wachstums selbst wächst exponentiell. Diese Beobachtungen gelten nicht nur für die Annahme der Fortsetzung des Moore'schen Gesetzes (d. H. Einer exponentiellen Verringerung der Größe von Transistoren in einer integrierten Schaltung), sondern basieren auf einem repräsentativen Modell verschiedener technologischer Prozesse. Dies zeigt deutlich, dass sich die Technologie und insbesondere das Tempo des technologischen Wandels in (zumindest) geometrischen Fortschritten und nicht linear beschleunigt, und dies geschieht ab dem Moment der Entstehung von Technologie und Technologie, aber tatsächlich ab dem Moment der Evolution auf der Erde.

Ich betone diesen Punkt, weil hier die Prognostiker, die zukünftige Trends berücksichtigen und über eine mögliche Zukunft sprechen, ihren größten Fehler machen. Die meisten technologischen Prognosen ignorieren im Allgemeinen die Art des „historisch-exponentiellen“ technologischen Fortschritts. Aus diesem Grund neigen die Menschen dazu, zu überschätzen, was kurzfristig erreicht werden kann (weil wir dazu neigen, die notwendigen Details zu verwerfen), aber zu unterschätzen, was langfristig erreicht werden kann (weil exponentielles Wachstum ignoriert wird).

Das Gesetz der beschleunigten Rückkehr

Wir können diese Beobachtungen wie folgt in das Gesetz der Beschleunigung der Rendite einteilen:

• Die Evolution nutzt positives Feedback so, dass effizientere Methoden, die sich aus einer Stufe des evolutionären Fortschritts ergeben, zur Schaffung der nächsten Stufe verwendet werden. Ergebend,
• Die Evolutionsrate eines Evolutionsprozesses nimmt mit der Zeit exponentiell zu. Mit der Zeit nimmt die „Reihenfolge“ der im Evolutionsprozess enthaltenen Informationen zu (dh das Maß dafür, wie gut diese Informationen zum Ziel passen, welches Überleben sich im Evolutionsprozess befindet).
• Dementsprechend wächst die „Rückkehr“ des Evolutionsprozesses (z. B. Geschwindigkeit, Kosteneffizienz oder die gesamte „Leistung“ des Prozesses) im Laufe der Zeit exponentiell.
• In einer anderen Kette positiver Rückmeldungen werden immer mehr Ressourcen für die Weiterentwicklung dieses Prozesses bereitgestellt, wenn ein bestimmter Evolutionsprozess (z. B. Berechnung) effizienter (z. B. kostengünstiger) wird. Dies führt zu einer zweiten Ebene des exponentiellen Wachstums (dh die Rate des exponentiellen Wachstums selbst wächst exponentiell).
• Die biologische Evolution ist ein solcher Evolutionsprozess.
• Die technologische Evolution ist ein weiterer solcher Evolutionsprozess. In der Tat hat die Entstehung des ersten Typs, der Technologie schafft, zu einem neuen evolutionären Prozess der Technologie geführt. Die technologische Evolution ist somit ein Produkt und eine Fortsetzung der biologischen Evolution.
• Ein bestimmtes Paradigma (eine Methode oder ein Ansatz zur Lösung eines Problems, z. B. die Reduzierung der Fläche eines Transistors auf einer integrierten Schaltung als Ansatz zur Schaffung leistungsfähigerer Computer) sorgt für ein exponentielles Wachstum, bis die Methode ihr volles Potenzial erreicht. In diesem Fall findet ein Paradigmenwechsel (dh ein grundlegender Ansatzwechsel) statt, der es ermöglicht, das exponentielle Wachstum fortzusetzen.

Wenn wir diese Prinzipien auf der höchsten Evolutionsstufe der Erde anwenden, führte der erste Schritt, die Schaffung von Zellen, das Paradigma der Biologie ein. Das anschließende Auftauchen von DNA bot eine digitale Möglichkeit, die Ergebnisse von Evolutionsexperimenten aufzuzeichnen. Dann verursachte die Entwicklung einer Spezies, die rationales Denken mit einem entgegengesetzten (d. H. Daumen) Finger kombinierte, einen grundlegenden Paradigmenwechsel von der Biologie zur Technologie. Der bevorstehende Wechsel des Hauptparadigmas wird vom biologischen zum hybriden Denken führen und biologisches und nicht-biologisches Denken kombinieren. Dieser Hybrid wird Stoffwechselprozesse beinhalten, die sich aus der Rekonstruktion und dem Kopieren der Prinzipien des biologischen Gehirns ergeben.

Wenn wir das Timing dieser Phasen untersuchen, sehen wir, dass sich der Prozess ständig beschleunigt. Die Entwicklung der Lebensformen dauerte Milliarden von Jahren für die ersten Schritte (zum Beispiel zu einfachen Zellen); weitere Fortschritte beschleunigt. Während der kambrischen Explosion dauerten Änderungen in den grundlegenden Paradigmen nur einige zehn Millionen Jahre. Später entwickelten sich Humanoiden über mehrere Millionen Jahre und Homo sapiens nur wenige hunderttausend.

Mit dem Aufkommen der technologieschaffenden Spezies wurde das exponentielle Tempo für die Evolution durch DNA-gesteuerte Proteinsynthese zu schnell und auf vom Menschen hergestellte Technologien umgestellt. Technologie geht über den einfachen Werkzeugbau hinaus; Es ist ein Prozess zur Schaffung immer leistungsfähigerer Technologien unter Verwendung von Werkzeugen aus der vorherigen Innovationsrunde. In diesem Sinne unterscheidet sich die menschliche Technologie von der Herstellung von Werkzeugen anderer Arten. Jede Phase der Technologieentwicklung ist festgelegt und dient als Grundlage für die nächste Phase.

Die ersten technologischen Schritte (Steinwerkzeuge, Feuer, Rad) dauerten Zehntausende von Jahren. Für die Menschen in dieser Zeit waren technologische Veränderungen selbst über Tausende von Jahren kaum spürbar. Um 1000 n. Chr. Waren die Fortschritte viel schneller und ein Paradigmenwechsel fand in nur ein oder zwei Jahrhunderten statt. Im neunzehnten Jahrhundert sahen wir mehr technologischen Wandel als in den neun Jahrhunderten davor. Dann, in den ersten zwanzig Jahren des zwanzigsten Jahrhunderts, sahen wir eine bedeutendere Entwicklung als im gesamten neunzehnten Jahrhundert. Jetzt findet der Paradigmenwechsel in nur wenigen Jahren statt. Das World Wide Web in seiner jetzigen Form existierte noch vor wenigen Jahren nicht und vor zehn Jahren überhaupt nicht.

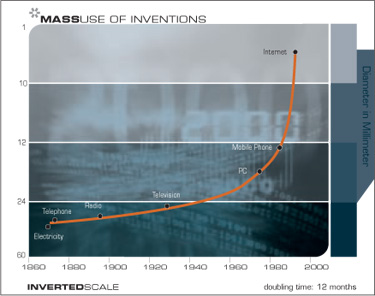
Die Geschwindigkeit des Paradigmenwechsels (d. H. Die Gesamtgeschwindigkeit des technologischen Fortschritts) verdoppelt sich derzeit (ungefähr) alle zehn Jahre; Das heißt, die Zeit für einen Paradigmenwechsel halbiert sich alle zehn Jahre (und die Wachstumsrate selbst wächst exponentiell). Der technologische Fortschritt im 21. Jahrhundert wird also dem entsprechen, was (in einer linearen Darstellung) etwa 200 Jahrhunderte erforderlich gemacht hätte. Im Gegenteil, das zwanzigste Jahrhundert verging nur etwa 25 Jahre des Fortschritts (wiederum in Bezug auf sein derzeitiges Tempo), da seine Geschwindigkeit auf das derzeitige erhöht wurde. So wird das 21. Jahrhundert fast tausendmal größere technologische Veränderungen erleben als sein Vorgänger.

Singularität nahe

Um die Natur und Bedeutung der bevorstehenden „Singularität“ zu erkennen, ist es wichtig, die Natur des exponentiellen Wachstums zu verstehen. Zu diesem Zweck erzähle ich gerne eine Geschichte über den Erfinder des Schachs und seinen Schutzpatron, den Kaiser von China. Als Reaktion auf das Angebot des Kaisers, eine Belohnung für sein neues Lieblingsspiel zu ernennen, bat der Erfinder, ein Reiskorn auf das erste Feld des Schachbretts zu legen, zwei auf das zweite Feld, vier auf das dritte und so weiter. Der Kaiser stimmte dieser scheinbar einfachen und bescheidenen Bitte schnell zu. Einer Version dieser Geschichte zufolge ging der Kaiser bankrott, da 63 Verdopplungen letztendlich 18 Millionen Billionen Reiskörner ausmachen. Angesichts der Tatsache, dass zehn Reiskörner einen Quadratzoll bedecken, erfordert diese Reismenge Reisfelder, die die doppelte gesamte Erdoberfläche einschließlich der Ozeane bedecken. In einer anderen Version dieser Geschichte verlor der Erfinder den Kopf.

Es sollte angemerkt werden, dass, als der Kaiser und Erfinder die erste Hälfte des Schachbretts füllten, alles ganz gut lief. Dem Erfinder wurden Löffel Reis, dann eine Schüssel Reis und dann Fässer gegossen. Am Ende der ersten Hälfte des Schachbretts hatte der Erfinder bereits ein großes Reisfeld (4 Milliarden Körner), und der Kaiser bemerkte, dass etwas nicht stimmte. Als sie in die zweite Hälfte des Schachbretts gingen, begann sich die Situation rapide zu verschlechtern. In Bezug auf die Verdoppelung der Berechnungen haben wir seit der Erfindung der ersten programmierbaren Computer am Ende des Zweiten Weltkriegs im Moment etwas mehr als zweiunddreißig Verdoppelungen ihrer Produktivität erreicht.

Dies ist die Natur des exponentiellen Wachstums. Obwohl die Technologie exponentiell wächst, leben wir Menschen in einer linearen Welt. Aus diesem Grund sehen technologische Trends für uns nicht wie die ersten Schritte im Prozess der ständigen Verdoppelung der technologischen Leistung aus. Dann zeigt die Technologie scheinbar aus dem Nichts ein explosives Wachstum. Als beispielsweise das Internet in den 1980er Jahren in zwei Jahren von 20.000 auf 80.000 Knoten stieg, blieb dieser Fortschritt der Öffentlichkeit verborgen. Zehn Jahre später, als es im gleichen Zeitraum von 20 Millionen auf 80 Millionen Knoten wuchs, war der Einfluss bereits spürbar.

Während sich das exponentielle Wachstum in der ersten Hälfte des 21. Jahrhunderts weiter beschleunigt, werden wir das Gefühl einer Explosion der Unendlichkeit haben, zumindest aus Sicht der modernen Menschen, die durch eine lineare Perspektive begrenzt sind. Der Fortschritt wird letztendlich so schnell eintreten, dass unsere Fähigkeit, mit ihm Schritt zu halten, zerstört wird. Er wird buchstäblich außer Kontrolle geraten. Die Illusion, wir könnten den Schalter ziehen, wird zerstreut.

Kann der technologische Fortschritt unendlich weiter beschleunigen? Gibt es einen Moment, in dem die Leute nicht so schnell denken können, um mitzuhalten? Für gewöhnliche Menschen ist dies offensichtlich so. Was können jedoch tausend Wissenschaftler erreichen, von denen jeder tausendmal schlauer ist als der heutige Wissenschaftler und von denen jeder tausendmal schneller handelt als moderne Menschen (weil die Verarbeitung von Informationen in ihrem hauptsächlich nicht biologischen Gehirn schneller ist)? Ein Jahr kann gleich dem Jahrtausend sein. Was würden sie sich einfallen lassen?

Zunächst einmal würden sie eine Technologie entwickeln, um noch intelligenter zu werden (da ihre Intelligenz nicht mehr auf Leistung beschränkt ist). Sie würden beginnen, ihre eigenen Denkprozesse zu ändern, um noch schneller zu denken. Wenn sich Wissenschaftler millionenfach schlauer entwickeln und millionenfach schneller arbeiten, entspricht ihre Stunde einem ganzen Jahrhundert Fortschritt (nach heutigen Maßstäben).

Dies wird die Singularität sein. Eine Singularität ist ein technologischer Wandel, der so schnell und tiefgreifend ist, dass er das eigentliche Gefüge der menschlichen Geschichte durchbricht. Einige werden sagen, dass es unmöglich ist, die Singularität zu verstehen, zumindest mit unserem gegenwärtigen Verständnisniveau, und daher ist es unmöglich, über ihren „Ereignishorizont“ hinauszuschauen und zu verstehen, was danach passieren wird.

Meiner Meinung nach haben wir trotz der schwerwiegenden Einschränkungen des Denkens durch unser biologisches Gehirn, das nur hundert Billionen interneuronale Verbindungen aufweist, dennoch genügend abstrakte Denkkraft, um signifikante Schlussfolgerungen über die Natur des Lebens nach der Singularität zu ziehen. Aus meiner Sicht ist das Wichtigste, dass der aufkommende Intellekt weiterhin die menschliche Zivilisation repräsentiert, die bereits Mensch-Maschine ist. Dies wird der nächste Schritt in der Evolution sein, der nächste Paradigmenwechsel auf hoher Ebene.

Um das Konzept der Singularität in der Perspektive zu bewerten, schauen wir uns die Geschichte des Wortes selbst an. — , . , , , . , , . , . , , , , . , .

1950- (John Von Neumann) , « … , , , .» 1960- , (Irving John Good) « », , . 1986 , (Vernor Vinge), - (San Diego State University), «» - . , 1993 , , , , , , , « , », .

, . , , , . , , , , . , , . , «» , . , , .

, 1980- , « » , , , , . 20 , , , , .

. . , . ( ) , . , , . , , , , .

, , , . , «» , , . , : , , , -, , . , , .

, , , , .

, , . , , « ». , , Intel, 1970- , 24 . , , , , .

, 2019 . , , . , ?

.

( ) $1000 ( ) 49 , , .

, , , .

, , .

, , , -. ( ), , 1890 , «Robinson», , , CBS, , , , , , ( ) .

- . 49 ( ), . , , . , . ( ) 1910 1950 , 1950 1966 , .

? ? . « », (Randy Isaac), IBM? - ?

, ( ) , . . : , MIPS- ( ) , MIPS- .

, , . ( ), , , . «» ( , , , , ). , , , , , , , .

, ( 1958 ), ( 1947 ), , 1890 1900 . , .

Offensichtlich ist das sechste Paradigma nach Moores Gesetz im zweiten Jahrzehnt dieses Jahrhunderts erschöpft. Chips sind heute flach (obwohl bis zu 20 Materialschichten erforderlich sind, um eine Schicht der Schaltung herzustellen). Im Gegensatz dazu ist unser Gehirn in drei Dimensionen organisiert. Wir leben in einer dreidimensionalen Welt. Warum nicht die dritte Dimension nutzen? Das menschliche Gehirn verwendet tatsächlich einen sehr ineffizienten, digital gesteuerten elektrochemischen analogen Rechenprozess. Die meisten Berechnungen werden in Interneuronverbindungen mit einer Geschwindigkeit von nur etwa 200 Operationen pro Sekunde (bei jeder Verbindung) durchgeführt, was etwa zehn Millionen Mal langsamer ist als bei modernen elektronischen Schaltungen. Aber das Gehirn bezieht seine atemberaubende Kraft aus seiner hochparallelen Organisation in drei Dimensionen. Es gibt bereits viele Technologien auf dem Weg, die in drei Dimensionen arbeiten. Beispielsweise bauen Nanoröhren, die bereits in Laboratorien arbeiten, Schaltkreise aus fünfeckigen Anordnungen von Kohlenstoffatomen. Ein Kreislauf von fünfzehn Kubikzentimetern Nanoröhren ist millionenfach leistungsfähiger als das menschliche Gehirn. Es werden mehr als genug neue Computertechnologien untersucht, darunter dreidimensionale Siliziumchips, optische Berechnungen, kristalline Berechnungen, DNA-basierte Berechnungen und Quantenberechnungen, um die Wirkung des Gesetzes der beschleunigten Rückkehr, wie es auf die Computertechnologie angewendet wird, für lange Zeit beizubehalten.

Somit ist das (doppelte) exponentielle Wachstum des Rechnens breiter als das Moore'sche Gesetz, das sich nur auf eines der Paradigmen dieses Wachstums bezieht. Und diese Beschleunigung der Entwicklung der Computertechnologie ist wiederum Teil eines noch umfassenderen Phänomens der Beschleunigung des Tempos eines Evolutionsprozesses. Kritiker weisen schnell darauf hin, dass die Extrapolation eines exponentiellen Trends darauf beschränkt ist, dass „Ressourcen“ ausgehen. Ein klassisches Beispiel ist die folgende Situation: Wenn eine Art in einem neuen Lebensraum auftritt (z. B. Kaninchen in Australien), wächst die Anzahl einer Art für einige Zeit exponentiell, aber wenn Ressourcen wie ein Ort und Nahrung zur Neige gehen, stößt die Anzahl an die Wachstumsgrenze .

Die Ressourcen, die dem exponentiellen Wachstum des Evolutionsprozesses zugrunde liegen, sind jedoch relativ unbegrenzt:

1. Die Ordnung (ständig wachsend) des Evolutionsprozesses selbst. Jede Evolutionsstufe bietet leistungsfähigere Werkzeuge für die nächste. In der biologischen Evolution bildete das Aufkommen der DNA die Grundlage für leistungsfähigere und schnellere evolutionäre „Experimente“. Später eröffnete das Entstehen verschiedener „Strukturen“ von Organismen während der kambrischen Explosion den Weg für die rasche evolutionäre Entwicklung anderer Organe des Körpers wie des Gehirns. Um ein neueres Beispiel zu nennen: Das Aufkommen computergestützter Entwurfswerkzeuge kann die Erstellung der nächsten Computergeneration beschleunigen.
2. Das "Chaos" der Umgebung, in der der Evolutionsprozess stattfindet und das Optionen für eine noch größere Vielfalt bietet. In der biologischen Evolution tritt Diversität in Form von Mutationen und sich ständig ändernden Umweltbedingungen in den Prozess ein. In der technologischen Entwicklung geht die Unterstützung des Innovationsprozesses zu Lasten des menschlichen Einfallsreichtums in Kombination mit sich ständig ändernden Marktbedingungen.

Das eigentliche Problem ist das maximale Potenzial von Materie und Energie, in dem intellektuelle Prozesse funktionieren. Nach meinen Vorbildern werden wir im laufenden Jahrhundert jedoch nicht an ihre Grenzen stoßen (dies wird jedoch in den nächsten Jahrhunderten zu einem Problem werden).

Wir müssen auch zwischen einer „S-förmigen Kurve“ (einem nach rechts gestreckten „S“, das ein sehr langsames, fast nicht wahrnehmbares Wachstum, gefolgt von einem sehr schnellen Wachstum und einer anschließenden Abflachung, wenn sich der Prozess einer Asymptote nähert) unterscheiden, die charakteristisch ist für ein bestimmtes technologisches Paradigma und das anhaltende exponentielle Wachstum, das für die fortschreitende evolutionäre Entwicklung der Technologie charakteristisch ist. Spezifische Paradigmen wie das Moore'sche Gesetz erreichen schließlich Niveaus, bei denen ein exponentielles Wachstum nicht mehr möglich ist. Somit ist Moores Gesetz eine S-förmige Kurve. Das Wachstum der Rechenleistung ist jedoch ein kontinuierlicher exponentieller Prozess (zumindest bis wir das Universum mit dem Intellekt unserer Mensch-Maschine-Zivilisation „sättigen“, aber dies wird im kommenden Jahrhundert keine Einschränkung darstellen). In Übereinstimmung mit dem Gesetz der Beschleunigung der Rendite verwandelt ein Paradigmenwechsel, auch Innovation genannt, die S-Kurve eines bestimmten Paradigmas in eine Fortsetzung des exponentiellen Wachstums. Ein neues Paradigma (zum Beispiel dreidimensionale Schemata) setzt sich durch, wenn sich das alte Paradigma seiner natürlichen Grenze nähert. In der Geschichte des Rechnens ist dies bereits mindestens viermal geschehen. Dieses Merkmal unterscheidet auch die Herstellung von Werkzeugen für andere Tierarten, bei denen die Fähigkeit zur Herstellung (oder Verwendung) der Werkzeuge für jedes einzelne Tier durch eine scharf endende S-förmige Lernkurve gekennzeichnet ist, von Technologien, die von Menschen entwickelt wurden und seitdem eine exponentielle Wachstumsrate aufweisen Schöpfung.

DNA-Sequenzierung, Gedächtnis, Kommunikation, Internet und Miniaturisierung

Das „Gesetz zur Beschleunigung der Rendite“ gilt für jede Technologie, für jeden wirklich evolutionären Prozess und kann für die Informationstechnologie mit erstaunlicher Genauigkeit gemessen werden. Es gibt viele Beispiele für exponentielles Wachstum, das sich aus dem Gesetz zur Beschleunigung der Rendite in so unterschiedlichen technologischen Bereichen wie DNA-Sequenzierung, Kommunikationsgeschwindigkeit, Elektronik aller Art und sogar in schnell abnehmenden charakteristischen technologischen Größen ergibt. Die Singularität ergibt sich nicht aus einer einzigen exponentiellen Explosion der Rechengeschwindigkeit, sondern aus der Interaktion und Synergie, die sich aus der vielfältigen Verflechtung verschiedener technologischer Revolutionen ergeben. Sie müssen auch bedenken, dass jeder Punkt auf den exponentiellen Wachstumskurven, die diesem Arsenal von Technologien zugrunde liegen (siehe die folgenden Grafiken), ein ernstes menschliches Drama von Innovation und Wettbewerb darstellt. Überraschenderweise führen diese chaotischen Prozesse zu einer so reibungslosen und vorhersehbaren exponentiellen Abhängigkeit.

Als beispielsweise die Sequenzierung des menschlichen Genoms vor vierzehn Jahren begann, glaubten Kritiker, dass es angesichts der damals verfügbaren Sequenzierungsgeschwindigkeit mehrere tausend Jahre dauern könnte, bis das Projekt abgeschlossen ist. Trotzdem wurde das Projekt im fünfzehnten Jahr etwas früher als geplant abgeschlossen.

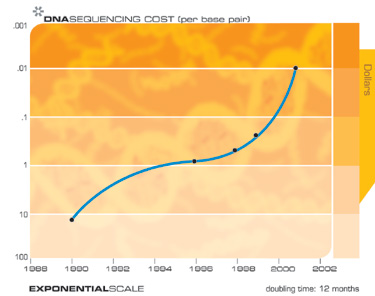
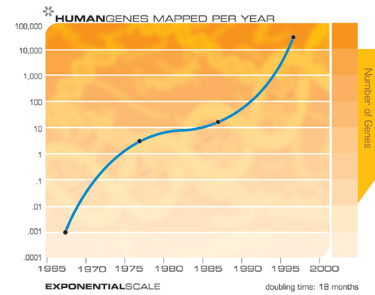
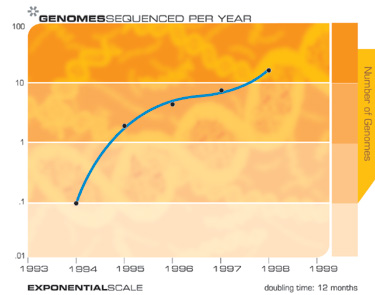
Natürlich erwarten wir ein exponentielles Wachstum der Technologie elektronischer Speichergeräte wie RAM (Random Access Memory).

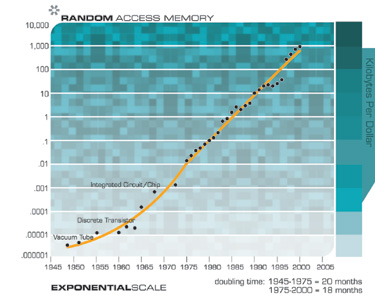
Beachten Sie, wie sich das exponentielle Wachstum mit dem Paradigmenwechsel von Vakuumröhren zu diskreten Transistoren und darüber hinaus zu integrierten Schaltkreisen fortsetzte.

Die Entwicklung der Magnetspeichertechnologie steht nicht in direktem Zusammenhang mit dem Moore Act, sondern basiert auf Fortschritten auf dem Gebiet der mechanischen und elektromagnetischen Systeme.

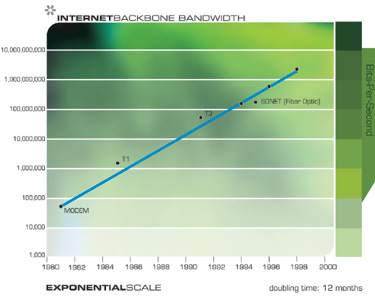
Das exponentielle Wachstum im Bereich der Kommunikationstechnologien war noch explosiver als im Bereich der Datenverarbeitung und in seinen Folgen nicht weniger bedeutend. Auch diese Beschleunigung hat eine viel breitere Basis als die bloße Reduzierung der Größe von Transistoren auf einem Chip und umfasst die Beschleunigung des Fortschritts bei Glasfaser, optischem Schalten, elektromagnetischer Technologie und vielem mehr.

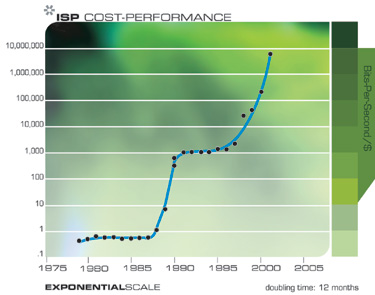
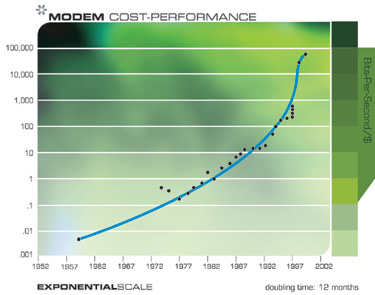
Achten Sie auf die Kaskade kleiner "S-förmiger" Kurven

Beachten Sie, dass wir in diesen beiden Diagrammen tatsächlich den Verlauf der „S-förmigen“ Kurven sehen können: Beschleunigung aufgrund des neuen Paradigmas, Stabilisierung, wenn das Paradigma ausfällt, und anschließende Wiederaufnahme des schnellen Wachstums nach dem Paradigmenwechsel.

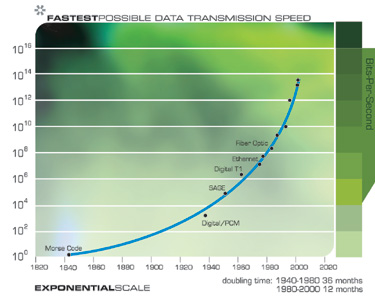
Die folgenden beiden Diagramme zeigen das Gesamtwachstum des Internets, ausgedrückt in Anzahl der Websites. Diese beiden Diagramme basieren auf denselben Daten, eines ist jedoch exponentiell und das andere linear. Wie ich bereits erwähnt habe, scheint sich die Technologie, die exponentiell voranschreitet, linear zu entwickeln. Daher wird es den meisten Beobachtern so erscheinen, als ob bis Mitte der neunziger Jahre, als das World Wide Web und die E-Mail aus dem Nichts heraus entstanden sind, nichts passiert ist. Die Umwandlung des Internets in ein globales Phänomen war jedoch viel früher leicht vorhersehbar, basierend auf Daten eines exponentiellen Trends.

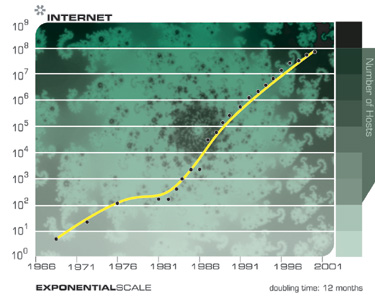
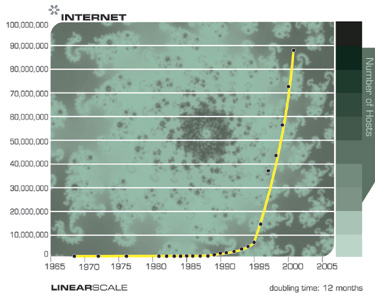
Achten Sie darauf, wie überraschend das explosive Wachstum des Internets auf einem Liniendiagramm aussieht und wie es auf einem Exponentialdiagramm vorhersehbar ist.

Am Ende werden wir uns vom Kabelsalat in unseren Städten und in unserem Leben der drahtlosen Kommunikation entziehen, deren Produktivität sich alle 10 bis 11 Monate verdoppelt.

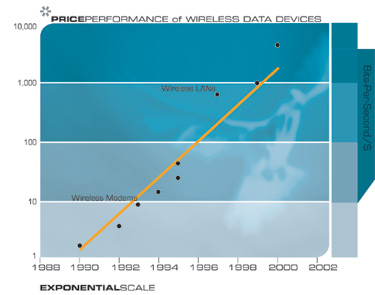
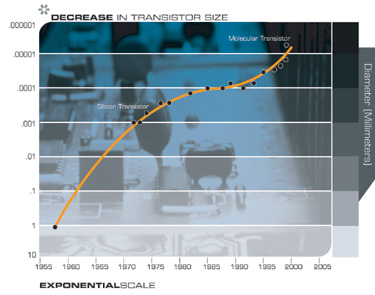
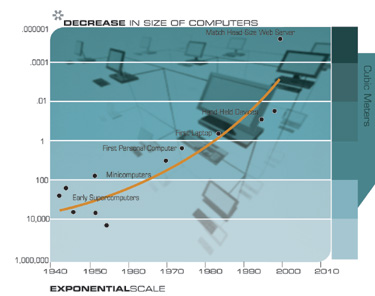
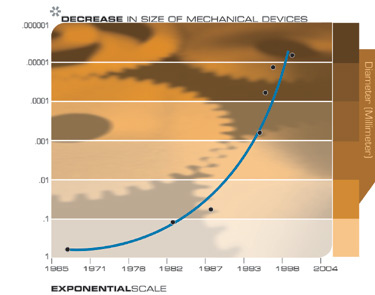
Eine andere Technologie, die weitreichende Konsequenzen für das 21. Jahrhundert haben wird, ist die weit verbreitete Tendenz, Dinge kleiner zu machen, dh Miniaturisierung. Die charakteristischen Abmessungen der Elemente einer Vielzahl von Technologien, sowohl elektronisch als auch mechanisch, werden reduziert und auch mit einer doppelten Exponentialrate. Gegenwärtig erfolgt die Verringerung der linearen Abmessungen für jede Dimension mit einem Koeffizienten von ungefähr 5,6 für jedes Jahrzehnt.

Zurück zum exponentiellen Wachstum des Computing

Wenn wir das exponentielle Wachstum des Rechnens in der richtigen Perspektive betrachten, als ein Beispiel für das weit verbreitete Auftreten eines exponentiellen Wachstums auf der Grundlage der Informationstechnologie, das eines von vielen Beispielen für das Gesetz der Beschleunigung der Rendite ist, können wir dessen Fortsetzung sicher vorhersagen.

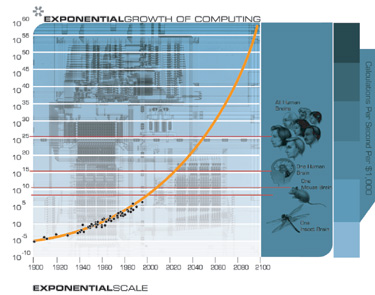
Im beigefügten Kasten gebe ich ein vereinfachtes mathematisches Modell des Gesetzes zur Beschleunigung der Rendite, das sich auf die (doppelte) exponentielle Zunahme der Rechenleistung bezieht. Aus den folgenden Formeln geht hervor, dass die obige Grafik die Berechnungsgeschwindigkeit kontinuierlich erhöht. Diese Grafik entspricht den für das 20. Jahrhundert verfügbaren Daten, durchläuft alle fünf Paradigmenwechsel und gibt eine Prognose für das 21. Jahrhundert. Bitte beachten Sie, dass die Wachstumsrate langsam, aber immer noch exponentiell ansteigt.

Das Gesetz der beschleunigten Rendite in Bezug auf das Wachstum des Computers

Das Folgende ist eine kurze Übersicht über das Gesetz zur Beschleunigung der Rendite am Beispiel eines doppelt exponentiellen Wachstums der Rechengeschwindigkeit. Dieses Modell betrachtet den Einfluss der wachsenden Macht der Technologie als Anreiz für die Entwicklung einer eigenen nächsten Generation. Zum Beispiel gewinnen wir mit leistungsfähigeren Computern und verwandten Technologien Werkzeuge und Wissen, um noch leistungsfähigere Computer zu entwickeln und sie noch schneller zu machen.

Bitte beachten Sie, dass die Daten für 2000 und nachfolgende Perioden Berechnungen in neuronalen Netzen darstellen, da erwartet wird, dass diese Art der Berechnung letztendlich dominiert, insbesondere bei der Emulation menschlicher Gehirnfunktionen. Diese Art der Berechnung ist kostengünstiger als herkömmliche Berechnungen (z. B. für Pentium III / IV) mit einem Koeffizienten von mindestens 100 (insbesondere wenn sie mithilfe von Digital-Analog-Elektronik implementiert werden, was den digital-Analog-Elektrochemieprozessen des Gehirns gut entspricht ) Der Koeffizient von 100 entspricht heute etwa sechs Jahren und weniger als sechs Jahren später im 21. Jahrhundert.

Meine Schätzung der Gehirnleistung beträgt 100 Milliarden Neuronen, multipliziert mit durchschnittlich 1000 Verbindungen pro Neuron (Berechnungen finden hauptsächlich in Verbindungen statt) und multipliziert mit 200 Operationen pro Sekunde. Natürlich sind diese Werte konservativ hoch, es können höhere und niedrigere Werte gefunden werden. Noch viel mehr (oder weniger) Bewertungen höherer Ordnung verschieben die Prognose jedoch nur um eine relativ kleine Anzahl von Jahren.

Einige der wichtigsten Daten für diese Analyse sind:

• Wir erreichen die Fähigkeiten eines menschlichen Gehirns (2 × 10 ¹⁶ CPS (Berechnungen pro Sekunde)) für 1000 USD um 2023.
• Wir erreichen die Fähigkeiten eines menschlichen Gehirns (2 × 10 ¹⁶ CPS) in einem Cent um 2037.
• Wir erreichen die Fähigkeiten der gesamten Menschheit (2 × 10 ²⁶ CPS) für 1000 USD um 2049.
• Wir erreichen die Fähigkeiten der gesamten Menschheit (2 × 10 ²⁶ CPS) in einem Cent um 2059.

Das Modell hat die folgenden Variablen:

• V: Geschwindigkeit (d. H. Produktivität) der Berechnungen (gemessen in Berechnungen pro Sekunde in Bezug auf ihren Wert)
• W: Weltweites Wissen in der Entwicklung und Herstellung von Computergeräten
• t: Zeit

Das Modell geht davon aus, dass:

• $$$V = C_1 \ cdot W$

Mit anderen Worten, die Leistung von Computern ist eine lineare Funktion des Wissens, wie man sie erstellt. In der Tat ist dies eine konservative Annahme. In der Regel verbessern Innovationen die V (Computerleistung) um ein Vielfaches und nicht um einen festen Betrag. Unabhängige Innovationen vervielfachen sich gegenseitig. Zum Beispiel eine neue Halbleitertechnologie wie CMOS, eine effizientere Layouttechnik für integrierte Schaltkreise und eine verbesserte Prozessorarchitektur wie Pipelining, unabhängig und multiplizieren V.

• $$$W = C_2 \ cdot \ int_0 ^ t V$

Mit anderen Worten, W (Wissen) ist kumulativ und das augenblickliche Inkrement des Wissens ist proportional zu V.

Dies gibt uns:

• $$$W = C_1 \ cdot C_2 \ cdot \ int_0 ^ t W$
• $$$W = C_1 \ cdot C_2 \ cdot _3 ^ {_4 \ cdot t}$
• $$$V = _1 ^ 2 \ cdot _2 \ cdot _3 ^ {_4 \ cdot t}$

Vereinfachung der Konstanten, die wir erhalten:

• $$$V = C_a \ cdot C_b ^ {C_c \ cdot t}$

Dies ist also die Formel für das "Beschleunigen" (dh das exponentielle Wachsen), das tatsächlich das "gewöhnliche Moore'sche Gesetz" ergibt.

Wie oben erwähnt, zeigen die Daten einen exponentiellen Anstieg der exponentiellen Wachstumsrate. (Wir haben die Rechenleistung zu Beginn des 20. Jahrhunderts alle drei Jahre, Mitte des Jahrhunderts alle zwei Jahre und in den 90er Jahren fast jedes Jahr verdoppelt.)

Schauen wir uns ein weiteres exponentielles Phänomen an, nämlich das Wachstum der Computerressourcen. Jedes der Computergeräte (mit den gleichen Kosten) wird nicht nur in Abhängigkeit von W immer leistungsfähiger, sondern ihre Anzahl, die für Berechnungen verwendet wird, wächst auch exponentiell.

So haben wir:

• N: Berechnungskosten
• $$$V = C_1 \ cdot W$ (wie zuvor)
• $$$N = _4 ^ {_5 \ cdot t}$ (Die Rechenkosten steigen exponentiell)
• $$$W = C_2 \ cdot \ int_0 ^ t (N \ cdot V)$

Nach wie vor sammelt sich das Weltwissen an, und das momentane Inkrement ist proportional zur Anzahl der Berechnungen, die den für die Berechnungen verwendeten Ressourcen (N) entsprechen, multipliziert mit der Leistung jedes Geräts (zu seinen konstanten Kosten).

Dies gibt uns:

• $$$W = C_1 \ cdot C_2 \ cdot \ int_0 ^ t (C_4 ^ {_5 \ cdot t} \ cdot W)$
• $$$W = C_1 \ cdot C_2 \ cdot (_3 ^ {_6 \ cdot t}) ^ {_7 \ cdot t}$
• $$$V = _1 ^ 2 \ cdot _2 \ cdot (_3 ^ {_6 \ cdot t}) ^ {_7 \ cdot t}$

Durch Vereinfachung der Konstanten erhalten wir:

• $$$V = C_a \ cdot (C_b ^ {_ \ cdot t}) ^ {C_d \ cdot t}$

Dies ist eine doppelte Exponentialkurve, in der die Exponentialwachstumsrate mit ihrer Exponentialgeschwindigkeit wächst.

Schauen wir uns nun die realen Daten an. Nehmen Sie die Parameter realer Computergeräte und Computer im 20. Jahrhundert:

• CPS / \ $ 1K: Berechnungen pro Sekunde für \ $ 1000

Daten zu Computergeräten des 20. Jahrhunderts entsprechen:

• CPS / \ $ 1K = $$$10 ^ {6,00 \ cdot \ frac {20,40} {6,00} ^ {\ frac {Jahr-1900} {100}} - 11,00}$

Wir können die Wachstumsrate über einen bestimmten Zeitraum bestimmen:

• Wachstumsrate =$$ $ inline $ 10 ^ {\ frac {\ log (CPS / \ $ 1K für \ hspace 5mu aktuelles \ hspace 5mu Jahr) - \ log (CPS / \ $ 1K für \ hspace 5mu vorheriges \ hspace 5mu Jahr}} {aktuelles \ hspace 5mu Jahr - vorheriges \ hspace 5mu Jahr}} $ inline $
• Das menschliche Gehirn = 100 Milliarden (10 ¹¹ ) Neuronen × 1000 (10 ³ ) Verbindungen pro Neuron × 200 (2 × 10 ² ) Berechnungen pro Sekunde pro Verbindung = 2 × 10 ¹⁶ Berechnungen pro Sekunde
• Menschliche Rasse = 10 Milliarden (10 ¹⁰ ) Menschen = 2 × 10 ²⁶ Berechnungen pro Sekunde

Diese Formeln geben die obigen Diagramme an.

Es wird bereits erwartet, dass der IBM Blue Gene-Supercomputer, dessen Fertigstellung für 2005 geplant ist, voraussichtlich 1 Million Milliarden Operationen pro Sekunde ausführen kann (d. H. Eine Milliarde Megaflops oder ein Petaflop). Dies ist bereits ein Zwanzigstel der Produktivität des menschlichen Gehirns, die ich konservativ auf 20 Millionen Milliarden Operationen pro Sekunde schätze (100 Milliarden Neuronen pro 1000 Verbindungen pro Neuron bei 200 Berechnungen pro Sekunde pro Verbindung). , 2010 , 2020 . 2030 ( ), , $1000. 2050 , $1000 , . , , . , , , ( ) . , . , . , . , , , , 200 - .

. . , , , . , , . , , , , , . , . — , .

, , , , . , . , , , , . , . , , . . -, .

— . , , . , ( , , ). , , , ; . , , .

, , . , . , .

, , , . , , , . « », , , . , . , , , . — , , , . , , , , , ( , — ).

— « » , . , , . , , ( ) . , , .

— : , , , , . , .

. , 10 http://www.nlm.nih.gov/research/visible/visible_human.html .

25 — , , . , , , .

, , , , , . (Andreas Nowatzyk) - (Carnegie Mellon University) 200 , , .

, - () , , , , , . , — , . , .

, . , , , , , . , , . , . , , , , .

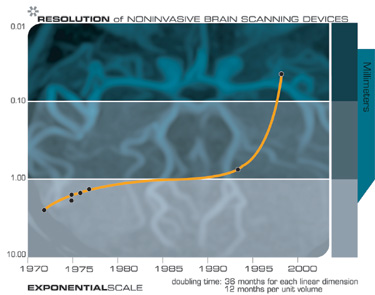
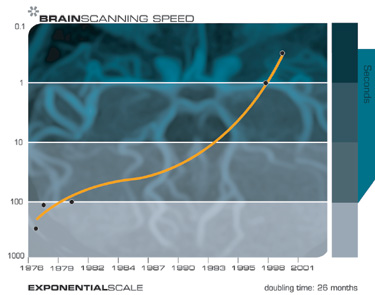
, — . 2030 «» ( ) , . — , , . . , , , ( , ).

, . , , , . , . . , , . , , , 2030 . - , , .

, ? , , . . . , , ( 100 , 1000 , ), , , .

, , , .. Microsoft Word. , , ( ). , - . , , . , .

. , , (Lloyd Watts — www.lloydwatts.com ) , . . , , , . , , . , (Hans Moravec) , 1000 , .

:

(Cochlea): . 30000 - .

. (MC — Multipolar Cells): .

. (GBC — Globular Bushy Cells): .

(Olivary Complex) ( ( LSO MSO)). .

. (SBC — Spherical Bushy Cells): , , .

. (OC — Octopus Cells): .

. (DCN — Dorsal Cochlear Nucleus): .

(VNTB — Ventral Nucleus of the Trapezoid Body): , .

, (VNLL — Ventral Nucleus of the Lateral Lemniscus, PON — Peri-Olivary Nuclei): .

(MSO — Medial Superior Olive): ( , , ).

(LSO — Lateral Superior Olive): .

(ICC — Central Nucleus of the Inferior Colliculus): .

(ICX — Exterior Nucleus of the Inferior Colliculus): .

(SC — Superior Colliculus): .

(MGB — Medial Geniculate Body):

(LS — Limbic System): , , , ..

(AC — Auditory Cortex)

— «Tabula Rasa» ( ), . « », , . , , .

, - , , . , , , . , .

, ---- -, ----. - , , , , , , . , , .

, . , . , , , , .

, , , . , (Ted Berger) Hedco Neurosciences , , . (Carver Mead) (CalTech) , - .

- (San Diego's Institute for Nonlinear Science) . ( - ) , « ». , , . ( ), , , . , , , , «». «» «» . (, , ), «» .

, - , . , - ( , «») , , . , . , .

, , . . , , , . — , .

, ( , ) , , . , , , , .

?

?

, «». , , . (, , ) . , , . , , .

, , ( ), . , — , , . , , . , , . , .

, . , , , «», . , , , , . — , , , . , , , - .

. « » (.. ), , «» . , ( ), , - .

, , , , , . , , .

, . «» , , . , - , «» , , , . , . , . , , .

. , , , . , . , , . , , .

, , : .

, , , , , . , , , , , : , , , , . , . , . .

, : , (.. ), ( ), , ..

. , ( ), . , ( ) , .

?

, : , , ? «» ? ?

. . , , , , - . (Marvin Minsky) , « - . , ».

, , . , , , ? , , ? , , , , ?

. «, », ? , , , , , .

, : « , , .» ?

, , , , ( ), ?

, ? , . , , . , — , — , , , , ( ) , , , , «» — ( ) , , , . : « , -, , , , , . , .

-!

? , ( ) . , . , , , .