Die mathematische Rechtfertigung für die Unangemessenheit, die Rolltreppe in der U-Bahn herunterzufahren

Entgegen den Regeln der U-Bahn rannte jeder von uns mindestens einmal in seinem Leben die Rolltreppe hinunter, um Zeit zu sparen. Auf den ersten Blick scheint dies absolut logisch und richtig zu sein: Wenn Sie schneller abreisen möchten, versuchen Sie, so früh wie möglich auf der Plattform zu sein. Fast sofort fällt Ihnen jedoch das folgende Szenario ein: Sie fahren kopfüber die Rolltreppe hinunter, gehen zur Plattform hinunter und die Autotüren schließen sich direkt vor Ihrer Nase. Während Sie auf den nächsten Zug warten, gehen Leute, die gleichzeitig mit der Zeit auf der Rolltreppe aufgestanden sind, leise hinunter und nehmen den nächsten Zug. In diesem Fall gibt es keinen Gewinn. Wie rational ist es also, die Rolltreppe herunterzufahren, und lohnt es sich überhaupt, dies zu tun? Ich beeile mich, Ihnen zu gefallen - die Antwort ist gefunden! Nachfolgend finden Sie eine mathematische Begründung für die Unzweckmäßigkeit (ja, es ist NICHT), die Rolltreppe in der U-Bahn herunterzufahren.

Aufgabenstellung

Bevor ich mich dem mathematischen Denken zuwende, ist es erwähnenswert, dass ich natürlich nicht der erste bin, der überhaupt über dieses Thema nachdenkt. Im Internet finden Sie eine ausreichende Anzahl von Artikeln und sogar Nachrichten von Bundeskanälen zu diesem Thema. Jedes Mal, wenn das Wesentliche solcher Experimente im üblichen Herunterfahren der Rolltreppe liegt, wird anschließend die gewonnene Zeit mit der Zeit der auf der Rolltreppe stehenden Person verglichen. Etwas besser, wenn die Autoren versuchen, die Wirksamkeit der Abfahrt zu beurteilen. Noch besser, wenn sie noch Statistiken liefern. Für die Statistik möchte ich mich übrigens etwas tiefer bedanken. Im Zusammenhang mit der Unklarheit dieser Experimente und dem Mangel an praktischen Schlussfolgerungen wurde eine Analyse des laufenden Prozesses konzipiert und anschließend durchgeführt.

Und so formulieren wir die Bedingungen des Problems und bezeichnen die Einschränkungen:

1. An dem (mentalen) Experiment sind zwei Personen beteiligt, die sich zu einem zufälligen Zeitpunkt gleichzeitig der Rolltreppe nähern und keine Ahnung haben, wo sich der Zug befindet.
2. Eine dieser Personen steht auf einer Rolltreppe und verbringt Zeit auf einem Abstieg. $$ gleich der Bewegungszeit der Rolltreppe.
3. Der zweite beschleunigt die Rolltreppe hinunter und erhöht die Geschwindigkeit $$ Zeiten, wodurch die Abstiegszeit um die gleiche Anzahl von Malen reduziert wird: $$ .
4. Effektiv wird ein derart beschleunigter Abstieg angesehen, der dazu führte, dass die auf der Rolltreppe stehende Person keine Zeit hat, in den Zug einzusteigen, in dem die auf der Rolltreppe entkommende Person Zeit zum Einsteigen hat.
5. Bezeichnen mit $$ - die Wahrscheinlichkeit eines effektiven Abstiegs. Dann ist eine Person gemäß dem Nash-Gleichgewicht nur dann bereit, ein Risiko einzugehen und die Rolltreppe herunterzulaufen, wenn die Wahrscheinlichkeit eines effektiven Abstiegs größer oder gleich der Wahrscheinlichkeit eines ineffektiven Abstiegs oder Stopps an Ort und Stelle ist, dh 0,5. Wenn die Wahrscheinlichkeit eines effektiven Abstiegs größer oder gleich 0,5 ist, wird die Entscheidung, die Rolltreppe herunterzufahren, als angemessen bezeichnet . Wenn weniger als 0,5 - unpraktisch .
6. Wir vernachlässigen die Tatsache, dass es im wirklichen Leben in der Regel notwendig ist, nach dem Verlassen der Rolltreppe einen weiteren Abstand zum Auto zu gehen oder darauf zu warten, dass Personen das Auto verlassen. Die Züge fahren in variablen Intervallen und stehen bewegungslos vor dem Öffnen und Schließen der Türen. Das heißt, wir gehen davon aus, dass, wenn sich der Zug zum Zeitpunkt des Verlassens der Rolltreppe am Bahnhof befindet, seine Türen geöffnet sind und der Versuchsteilnehmer sofort im Auto landet, der Zug selbst die Türen öffnet (schließt) und sofort und vom Bahnhof zum Bahnhof (vom Bahnhof) kommt dnomomentno.

Entscheidungsfortschritt

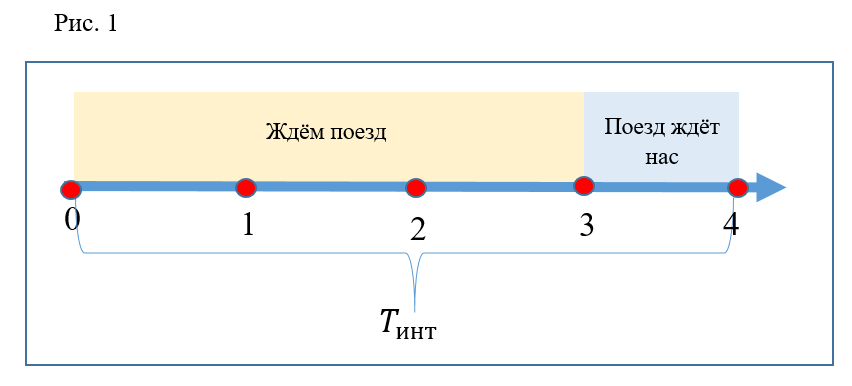
Zeichnen wir die Zeitachse (Abb. 1). Die gesamte Achse besteht aus aufeinanderfolgenden Intervallen zwischen den Zügen. Im Folgenden wird nur ein Intervall berücksichtigt. Teilen Sie das angezeigte Intervall in 4 gleiche Segmente. Punkt 0 auf dieser Achse entspricht dem Moment, in dem der Zug den Bahnhof verlässt. Punkt 3 entspricht der Ankunft des Zuges und dem Öffnen der Türen. Punkt 4 - Schließen der Türen und Abfahrt des Zuges. Zur Vereinfachung der grafischen Darstellung und Berechnung wird daher das Intervall zwischen den Zügen zwischen den Abfahrtsmomenten der Züge vom Bahnhof gezählt. Die ersten drei Segmente geben die Zeit an, in der die Fahrgäste auf den ankommenden Zug warten müssen. Das vierte Segment ist die Haltezeit des Zuges, in der die Fahrgäste einsteigen können. Setzen Sie auch diese Zeit $$ (Abstiegszeit auf der Rolltreppe) entspricht zwei Segmenten. Koeffizient $$ gleich 2, dh die Abstiegszeit läuft 2 mal kürzer und gleich einem Segment.



Nun, um die Wahrscheinlichkeit zu bestimmen $$ Finden Sie heraus, in welchem ​​Zeitraum die Entscheidung zum Joggen dazu führen wird, dass der Abstieg effektiv ist. Wenn sich unsere Teilnehmer beispielsweise zum Zeitpunkt 0 der Rolltreppe nähern, befindet sich der erste zum Zeitpunkt 0 auf der Plattform $$ (Abb. 2) und die zweite früher im Moment $$ . Wie aus der Abbildung hervorgeht, befindet sich zu keinem dieser Zeitpunkte ein Zug am Bahnhof, was bedeutet, dass das Herunterfahren ineffizient war.



Stellen Sie sich einen anderen Fall vor (Abb. 3): Die Teilnehmer des Experiments nähern sich zum Zeitpunkt 2 der Rolltreppe. Wie im vorherigen Fall befindet sich der erste zum Zeitpunkt auf der Plattform $$ und die zweite früher im Moment $$ . Es ist jedoch offensichtlich, dass der Zug zu beiden Zeiten am Bahnhof ist. Beide haben also Zeit, in denselben Zug einzusteigen, weshalb das Herunterfahren genauso ineffizient war.



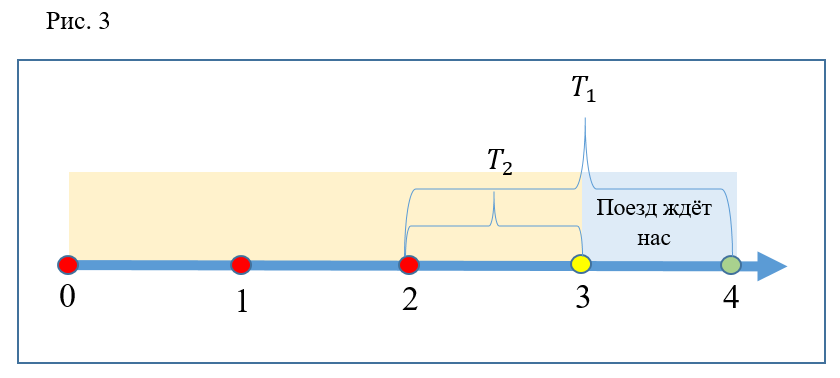
Ferner ist es leicht zu verstehen, dass zu jeder Zeit im Intervall von 2 bis 3 das Bergabfahren effektiv ist, da die entkommene Person immer in den Zug einsteigen kann und nicht die entkommene. Wenn Sie Zeitpunkte zwischen 3 und 4 wählen, kommen beide Teilnehmer zu spät zum Zug und müssen gemeinsam auf den nächsten warten, dh ein erneutes Fahren ist ineffektiv.

Es stellt sich heraus, dass es in 4 herkömmlichen Zeiträumen nur dann effektiv ist, herunterzufahren, wenn sich die Teilnehmer zwei- bis dreimal der Rolltreppe nähern (Abb. 4). Die Wahrscheinlichkeit, sich darauf einzulassen, beträgt 1/4. Unter den gegebenen Bedingungen der Aufgabe ist es daher unpraktisch, eine Entscheidung zum Herunterfahren zu treffen, da der zweite Teilnehmer mit größerer Wahrscheinlichkeit (mit einer Wahrscheinlichkeit von 3/4) vergeblich läuft und gezwungen sein wird, zusammen mit dem ersten, der später herunterfuhr, auf den Zug zu warten.



Die folgenden Bemerkungen sind völlig fair:

1. Die Intervalle zwischen den Zügen können sowohl verringert als auch erhöht werden. Die Parkzeit kann sich erhöhen und die Wartezeit kann sich verringern (mit demselben Intervall) und umgekehrt.
2. Die Geschwindigkeit der Rolltreppe ist konstant, aber die Abstiegszeit kann variieren, da die Stationen mehr oder weniger tief sein können.
3. Der zweite Teilnehmer läuft möglicherweise nicht zwei-, sondern drei- oder sogar viermal schneller als die Rolltreppe.

Um die Auswirkungen von Änderungen der oben genannten Faktoren beurteilen zu können, muss die Beziehung zwischen diesen Werten und der Wahrscheinlichkeit abgeleitet werden, zu einem Zeitpunkt auf die Rolltreppe zu gelangen, zu dem es effektiv ist, herunterzufahren.

Dazu stellen wir einen anderen Fall dar (Abb. 5). Wir lassen alle Originaldaten unverändert, mit Ausnahme von eins: Koeffizient $$ auf 4 erhöhen. Das heißt, der zweite Teilnehmer ist viermal schneller unten als der erste. Zur Vereinfachung des Bildes teilen wir unser Intervall in 8 gleiche Teile. Somit beträgt die Abstiegszeit auf der Rolltreppe jetzt 4 Segmente, der Zug hält um zwei, die Wartezeit beträgt 6 und die Abstiegszeit, um alleine zu fahren. Es ist nicht schwer herauszufinden, dass die Länge des „effektiven“ Zeitintervalls (von 4 bis 7 Zeitpunkten) jetzt 3 beträgt. Das heißt, die Wahrscheinlichkeit $$ gleich 3/8. Dies ist bereits mehr als im ersten Fall, aber wir haben diese Änderungen überhaupt nicht durchgeführt, um die Wahrscheinlichkeit zu bewerten.



Basierend auf Abbildung 4 und Abbildung 5 ist es offensichtlich, dass die Länge des „effektiven“ Segments beträgt $$ . Teilen Sie es durch die Länge des Intervalls und erhalten Sie die Wahrscheinlichkeit $$ wo $$ .
Wir führen eine Reihe von Transformationen durch: $$$$ .
Die endgültige Formel: $$ .

Basierend auf dieser Formel können mehrere grundlegende Schlussfolgerungen gleichzeitig gezogen werden:

1. Der Wahrscheinlichkeitswert wird durch Änderungen der Parkzeit und der Zugwartezeit nicht beeinflusst, wenn sich das Gesamtintervall nicht ändert (Abb. 6).
   
   
   
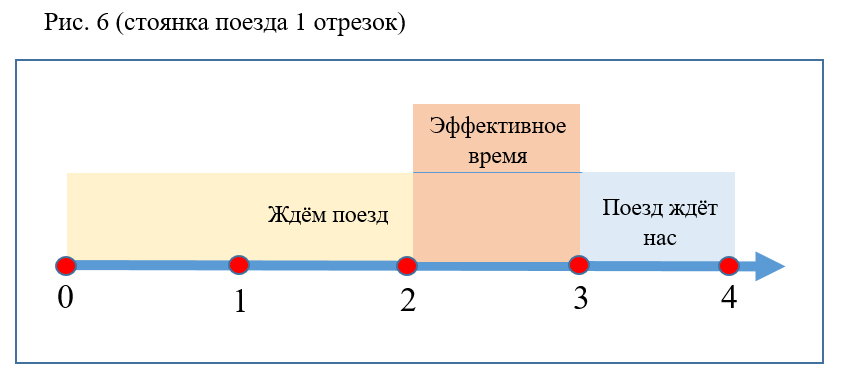
2. Je größer der Abstand zwischen den Zügen ist, desto geringer ist die Wahrscheinlichkeit P (Abb. 7).
   
   
   
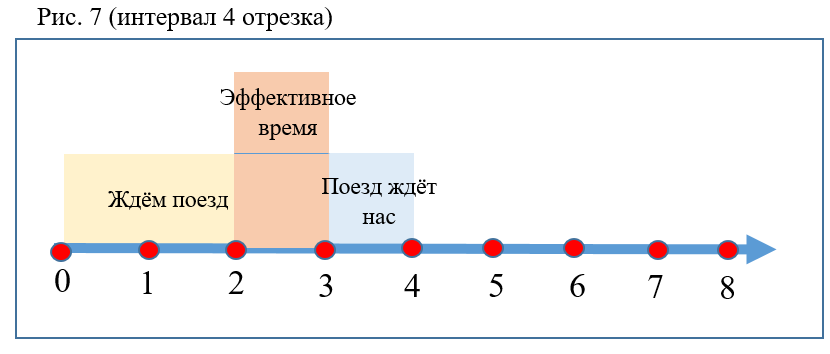
3. Die Wahrscheinlichkeit steigt, wenn das Verhältnis der Abstiegszeit auf der Rolltreppe zum Intervall und / oder der Koeffizient K zunimmt.
   

Treueprüfung

Nun wollen wir sehen, wie wahr die abgeleitete Formel ist.

Um die Richtigkeit der Formel zu überprüfen, wenden wir uns den Statistiken zu, die 2014 vom Korrespondenten von The Village sehr praktisch waren. Ich drücke meine Anerkennung aus und werde am Ende des Artikels natürlich einen Link zum Originalartikel hinterlassen. Es ist auch gut, dass die Statistiken als visuelle Infografiken dargestellt werden.

Experiment 1. U-Bahnstation Tschechowskaja



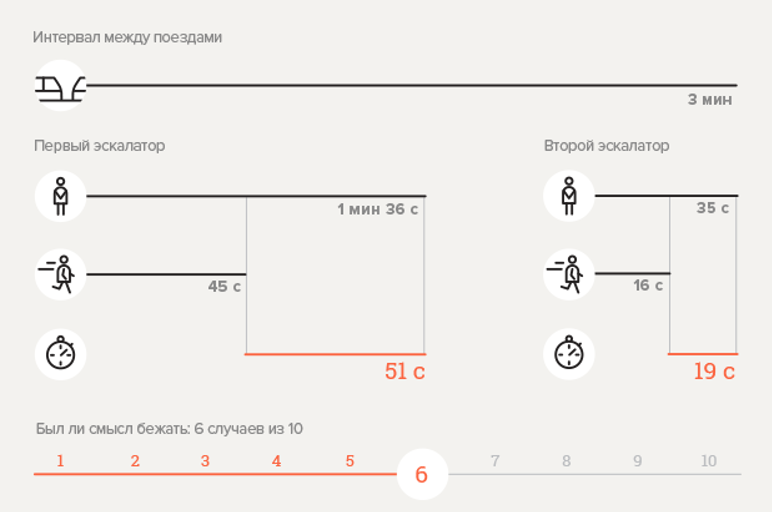
Berechnen Sie die Wahrscheinlichkeit $$ .
Hier $$ ; $$ ; $$ ; $$ ; $$ .

Das erhaltene Ergebnis weicht offenbar von den experimentellen Daten ab. Ist die Formel falsch? Nein! Aus der Infografik ist ersichtlich, dass der Abstieg zur Station eine Fahrt auf zwei Rolltreppen beinhaltet, die Übergangszeit zwischen ihnen jedoch nicht berücksichtigt wird. Wenn wir aus Gründen der Zuverlässigkeit davon ausgehen, dass der Übergang mindestens 30 Sekunden dauert, wird ein neuer Wert ersetzt $$ wir bekommen: $$ ; $$ , was dem experimentellen Ergebnis viel näher kommt. Es ist auch erwähnenswert, dass das Experiment nur 10 Wiederholungen vorsah. Durch Erhöhen der Anzahl der Wiederholungen ist es möglich, eine nahezu vollständige Übereinstimmung der berechneten Daten mit den während des Experiments erhaltenen Ergebnissen zu erreichen.

Experiment 2. U-Bahnstation "Victory Park"



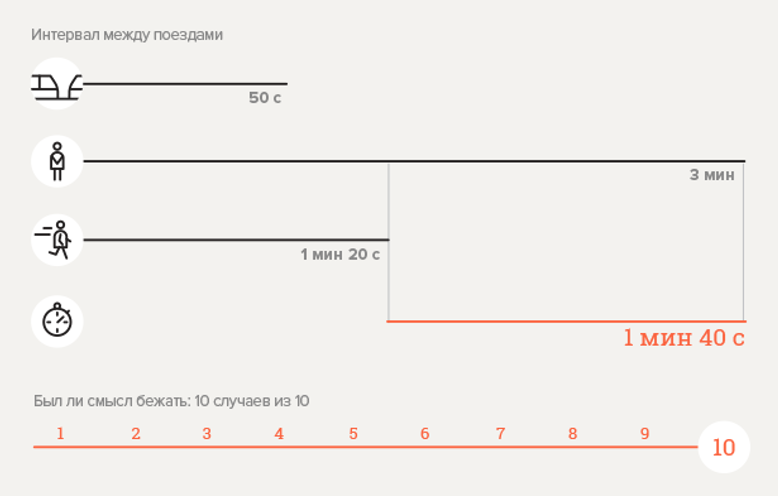
Berechnen Sie die Wahrscheinlichkeit $$ .
Hier $$ ; $$ ; $$ ; $$ ; $$ .
Es ist zu sehen, dass wir eine Wahrscheinlichkeit größer als eins haben. Aber hier gibt es keinen Widerspruch. Wenn Sie sich die allgemeine Form der Formel ansehen, wird deutlich, dass in dem Fall, in dem die Abstiegszeit auf der Rolltreppe gleich dem Intervall zwischen den Zügen ist, eine Erhöhung der Geschwindigkeit um mindestens das Zweifache die Wahrscheinlichkeit einer effektiven beschleunigten Abfahrt auf 0,5 erhöht. Wenn die Fahrzeit der Rolltreppe größer als das Intervall ist, dann mit demselben Koeffizienten $$ Die Wahrscheinlichkeit, früher in einen Zug zu steigen, steigt nur. Wenn die Abstiegszeit auf der Rolltreppe mindestens das Zweifache des Intervalls beträgt, ist die fahrende Person in 100% der Fälle pünktlich zum Zug, für den die verbleibende Person auf der Rolltreppe keine Zeit hat. Diesen Effekt beobachten wir in diesem Experiment: Der Korrespondent kam zu dem Schluss, dass er in 10 von 10 Fällen weggespült wurde.

Experiment 3. U-Bahnstation Park Kultury



Berechnen Sie die Wahrscheinlichkeit $$ .
Hier $$ ; $$ ; $$ ; $$ ; $$ .

Wieder ein Fehler? Überhaupt nicht. Es ist ersichtlich, dass, wie oben angegeben, die Abstiegszeit auf der Rolltreppe das Zweifache des Intervalls zwischen den Zügen beträgt. Die Laufzeit ist 2 mal kürzer. Es stellt sich heraus, dass jeder Abstieg effektiv sein sollte. Vergessen Sie jedoch nicht, dass wir vor Beginn der Diskussion davon ausgegangen sind, dass die Türen sofort geschlossen werden und der Zug zumindest sofort vom Bahnhof abfährt. Wenn Sie sich eine Option wie in Abbildung 8 vorstellen, wird deutlich, dass eine außer Kontrolle geratene Person im wirklichen Leben möglicherweise keine Zeit hat, sich an Punkt 1 zu setzen (zum Beispiel fährt der Zug etwas früher ab), und an Punkt 2 verzögert der Zug im Gegenteil etwas. und dann wird eine nicht rennende Person zusammen mit einer spät laufenden Person, die im vorherigen Zug fährt, darin sitzen.



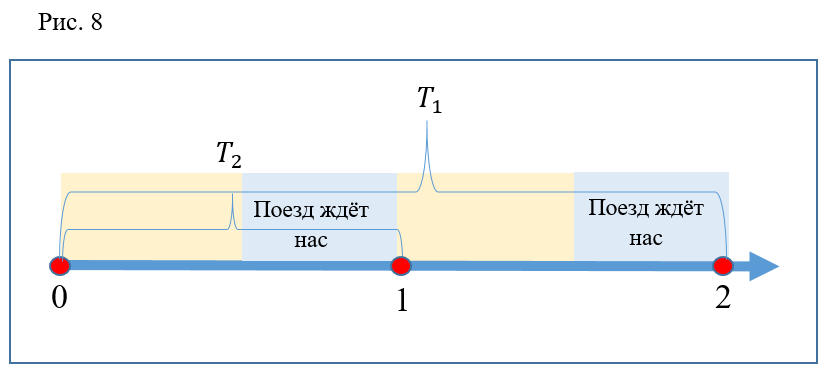
Ich nehme an, dass es in beiden "unwirksamen" Zeiten passiert ist. Es gibt allen Grund zu der Annahme, dass mit zunehmender Anzahl von Wiederholungen des Experiments der Prozentsatz der "effektiven" Läufe zu 100% tendiert.

Schlussfolgerungen

Nachdem es nun möglich war, anhand der verfügbaren experimentellen Daten die Richtigkeit der Formel zu bestätigen, werden wir sie analysieren und Schlussfolgerungen ziehen. Da wir uns von Anfang an einig waren, dass wir die Entscheidung, nach unten zu laufen, als zweckmäßig erachten würden, wenn die Wahrscheinlichkeit eines effektiven Abstiegs größer oder gleich 0,5 ist. Das heißt, wenn wir buchstäblich sicher sein können, dass wir in mindestens der Hälfte der Fälle aus gutem Grund laufen, lohnt es sich wirklich, das Risiko einzugehen und zu rennen, denn wenn wir zu spät kommen, verlieren wir praktisch nichts. Basierend auf dem Vorstehenden schreiben wir die Wahrscheinlichkeitsformel wie folgt um: $$ .

Es ist interessant, dass es, wie wir bereits herausgefunden haben, sinnvoll ist, immer wann zu rennen $$ . Gleichzeitig ist es auch wahr, dass wenn $$ Unabhängig davon, wie schnell Sie fahren, beträgt die Wahrscheinlichkeit, früher in einen Zug einzusteigen, weniger als 0,5, da dies offensichtlich ist $$ wird niemals größer oder gleich 1 sein.

Schauen wir uns nun die Geschwindigkeit des Korrespondenten an. Im Durchschnitt ist es ungefähr 2-mal so schnell wie die Rolltreppe (die Abstiegszeit ist 2-mal kürzer). Im Allgemeinen stimmen diese Daten mit den Ergebnissen meiner eigenen Experimente überein (ich sehe keinen Sinn darin, sie zu bringen). In der Regel ist es bereits schwierig, eine Geschwindigkeit mit einem K-Koeffizienten von mindestens 3 zu entwickeln: Es gibt viele Leute, die auf einer echten Rolltreppe nach unten rennen wollen, und außerdem können Menschen, die zu ihrer Linken stehen oder ihre Sachen (Taschen, Koffer) stören. Mittel $$ und $$ . Das heißt, eine Entscheidung zur Beschleunigung ist nur dann angemessen, wenn das Verhältnis $$ nicht weniger als 1. Und dies ist nur möglich, wenn die Abstiegszeit auf der Rolltreppe nicht kürzer ist als das Intervall zwischen den Zügen. In einer echten U-Bahn, in der das durchschnittliche Intervall zwischen den Zügen 2 Minuten beträgt, können nicht alle Bahnhöfe eine lange Abfahrt vorweisen. Selbst in der U-Bahn von St. Petersburg beträgt die Fahrzeit der Rolltreppe in der Regel etwa 1 Minute und 30 Sekunden, dh 0,75-mal weniger als das Intervall. Daraus folgt die sehr offensichtliche und wichtigste grundlegende Schlussfolgerung: Wenn Sie sicher sind, dass sich die Rolltreppe an diesem Bahnhof weniger als das Intervall zwischen den Zügen bewegt, ist es nicht praktikabel, daran entlang zu fahren.

PS Bitte berücksichtigen Sie die Tatsache, dass diese Aufgabe nicht die Notwendigkeit berücksichtigt, in einen bestimmten Wagen zu steigen. Es geht ausschließlich darum, auf den Bahnsteig zu steigen und dann in den Zug einzusteigen.

Experimentelle Datenquelle: The Village . Nochmals vielen Dank!