Der nachfolgend verwendete Datensatz stammt aus einem bereits bestandenen Kaggle-Wettbewerb
von hier .
Auf der Registerkarte Daten können Sie die Beschreibung aller Felder lesen.
Der gesamte Quellcode
ist hier im Laptop-Format.
Wir laden die Daten und überprüfen, ob wir im Allgemeinen Folgendes haben:
import numpy as np import pandas as pd dataset = pd.read_csv('../input/ghouls-goblins-and-ghosts-boo/train.csv')
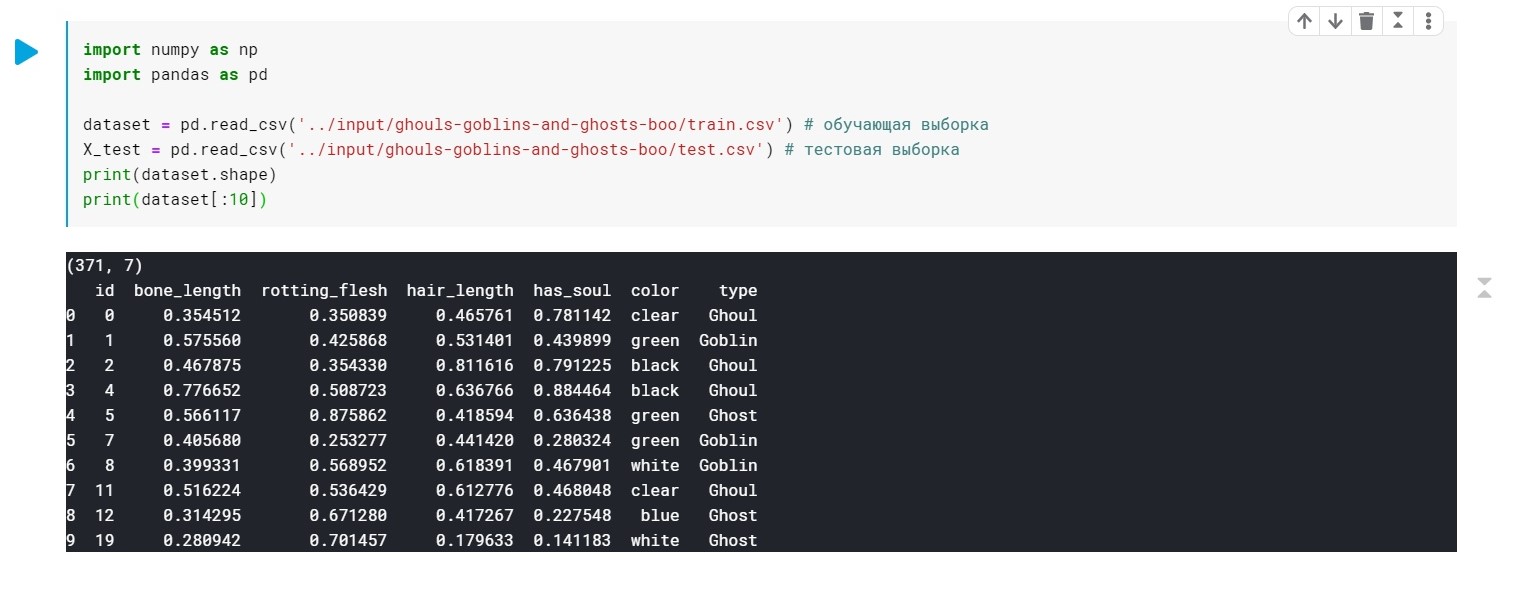
Die Werte des Typfeldes (Ghoul, Ghost, Goblin) werden einfach durch 0, 1 und 2 ersetzt.
Farbe - muss auch vorverarbeitet werden (wir benötigen nur numerische Werte, um das Modell zu erstellen). Wir werden dafür LabelEncoder und OneHotEncoder verwenden.
Weitere Details .
from sklearn.preprocessing import LabelEncoder, OneHotEncoder labelencoder_X_1 = LabelEncoder() X_train[:, 4] = labelencoder_X_1.fit_transform(X_train[:, 4]) labelencoder_X_2 = LabelEncoder() X_test[:, 4] = labelencoder_X_2.fit_transform(X_test[:, 4]) labelencoder_Y_2 = LabelEncoder() Y_train = labelencoder_Y_2.fit_transform(Y_train) one_hot_encoder = OneHotEncoder(categorical_features = [4]) X_train = one_hot_encoder.fit_transform(X_train).toarray() X_test = one_hot_encoder.fit_transform(X_test).toarray()
Nun, zu diesem Zeitpunkt sind unsere Daten fertig. Es bleibt unser Modell zu trainieren.
Zuerst
Adagrad auftragen :
Im Wesentlichen handelt es sich hierbei um eine Modifikation des stochastischen Gradientenabstiegs, über den ich das letzte Mal geschrieben habe:
habr.com/en/post/472300Diese Methode berücksichtigt den Verlauf aller vergangenen Gradienten für jeden einzelnen Parameter (die Idee der Skalierung). Auf diese Weise können Sie die Größe des Lernschritts für Parameter mit einem großen Gradienten reduzieren:
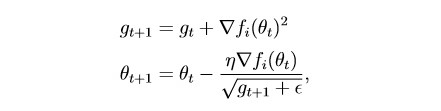
g ist der Skalierungsparameter (g0 = 0)
θ - Parameter (Gewicht)
epsilon ist eine kleine Konstante, die eingeführt wird, um eine Division durch Null zu verhindern
Teilen Sie den Datensatz in 2 Teile:
Trainingsmuster (Zug) und Validierung (val):
from sklearn.model_selection import train_test_split x_train, x_val, y_train, y_val = train_test_split(X_train, Y_train, test_size = 0.2)
Eine kleine Vorbereitung für das Modelltraining:
import torch import numpy as np device = 'cuda' if torch.cuda.is_available() else 'cpu' def make_train_step(model, loss_fn, optimizer): def train_step(x, y): model.train() yhat = model(x) loss = loss_fn(yhat, y) loss.backward() optimizer.step() optimizer.zero_grad() return loss.item() return train_step
Selbsttrainingsmodell:
from torch import optim, nn model = torch.nn.Sequential( nn.Linear(10, 270), nn.ReLU(), nn.Linear(270, 3)) lr = 0.01 n_epochs = 500 loss_fn = torch.nn.CrossEntropyLoss() optimizer = optim.Adagrad(model.parameters(), lr=lr) train_step = make_train_step(model, loss_fn, optimizer) from sklearn.utils import shuffle for epoch in range(n_epochs): x_train, y_train = shuffle(x_train, y_train)
Modellbewertung:
Hier haben wir zusätzlich zu den Ebenen (vorerst) nur 2 konfigurierbare Parameter:
Lernrate und n_epochs (Anzahl der Epochen).
Abhängig davon, wie wir diese beiden Parameter kombinieren, können drei Situationen auftreten:
1 - alles ist gut, d.h. Das Modell zeigt einen geringen Verlust bei der Trainingsprobe und eine hohe Genauigkeit bei der Validierung.
2 - Unteranpassung - großer Verlust an der Trainingsprobe und geringe Genauigkeit an der Validierungsprobe.
3 - Überanpassung - geringer Verlust bei der Trainingsprobe, aber geringe Genauigkeit bei der Validierung.
Mit dem ersten ist alles klar :)
Mit dem zweiten scheint es auch - mit der Lernrate und den n_epochs zu experimentieren.
Und was tun mit dem dritten? Die Antwort ist einfach - Regularisierung!
Zuvor hatten wir eine Verlustfunktion der Form:
L = MSE (Y, y) ohne zusätzliche Terme
Das Wesen der Regularisierung besteht genau darin, dass durch Hinzufügen eines Begriffs zur Zielfunktion der Gradient „fein“ wird, wenn er zu groß ist. Mit anderen Worten, wir beschränken unsere Zielfunktion.
Es gibt viele Regularisierungsmethoden. Weitere
Informationen zu L1 und L2 - Regularisierung:
craftappmobile.com/l1-vs-l2-regularization/#_L1_L2Die Adagrad-Methode implementiert die L2-Regularisierung. Wenden wir sie an!
Zur Verdeutlichung betrachten wir zunächst die Indikatoren des Modells ohne Regularisierung:
lr = 0,01, n_epochs = 500:
Verlust = 0,44 ...
Genauigkeit: 0,71
lr = 0,01, n_epochs = 1000:
Verlust = 0,41 ...
Genauigkeit: 0,75
lr = 0,01, n_epochs = 2000:
Verlust = 0,39 ...
Genauigkeit: 0,75
lr = 0,01, n_epochs = 3000:
Verlust = 0,367 ...
Genauigkeit: 0,76
lr = 0,01, n_epochs = 4000:
Verlust = 0,355 ...
Genauigkeit: 0,72
lr = 0,01, n_epochs = 10000:
Verlust = 0,285 ...
Genauigkeit: 0,69
Hier können Sie sehen, dass bei 4k + Epochen das Modell bereits überpasst ist. Versuchen wir nun, dies zu vermeiden:
Fügen Sie dazu den Parameter weight_decay für unsere Optimierungsmethode hinzu:
optimizer = optim.Adagrad(model.parameters(), lr=lr, weight_decay = 0.001)
Mit lr = 0,01 ist m_epochs = 10000:
Verlust = 0,367 ...
Genauigkeit: 0,73
In 4000 Epochen:
Verlust = 0,389 ...
Genauigkeit: 0,75
Es ist viel besser geworden, aber wir haben nur 1 Parameter im Optimierer hinzugefügt :)
Betrachten Sie nun SGDm (dies ist ein stochastischer Gradientenabstieg mit einer kleinen Ausdehnung - Heuristiken, wenn Sie möchten).
Unter dem Strich aktualisiert
SGD die Parameter nach jeder Iteration ziemlich stark. Es wäre logisch, den Gradienten mithilfe von Gradienten aus früheren Iterationen (der Idee der Trägheit) zu „glätten“:
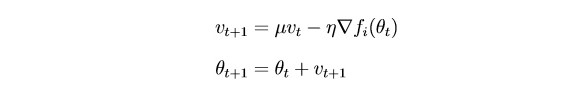
θ - Parameter (Gewicht)
µ - Trägheitshyperparameter
SGD ohne Impulsparameter:
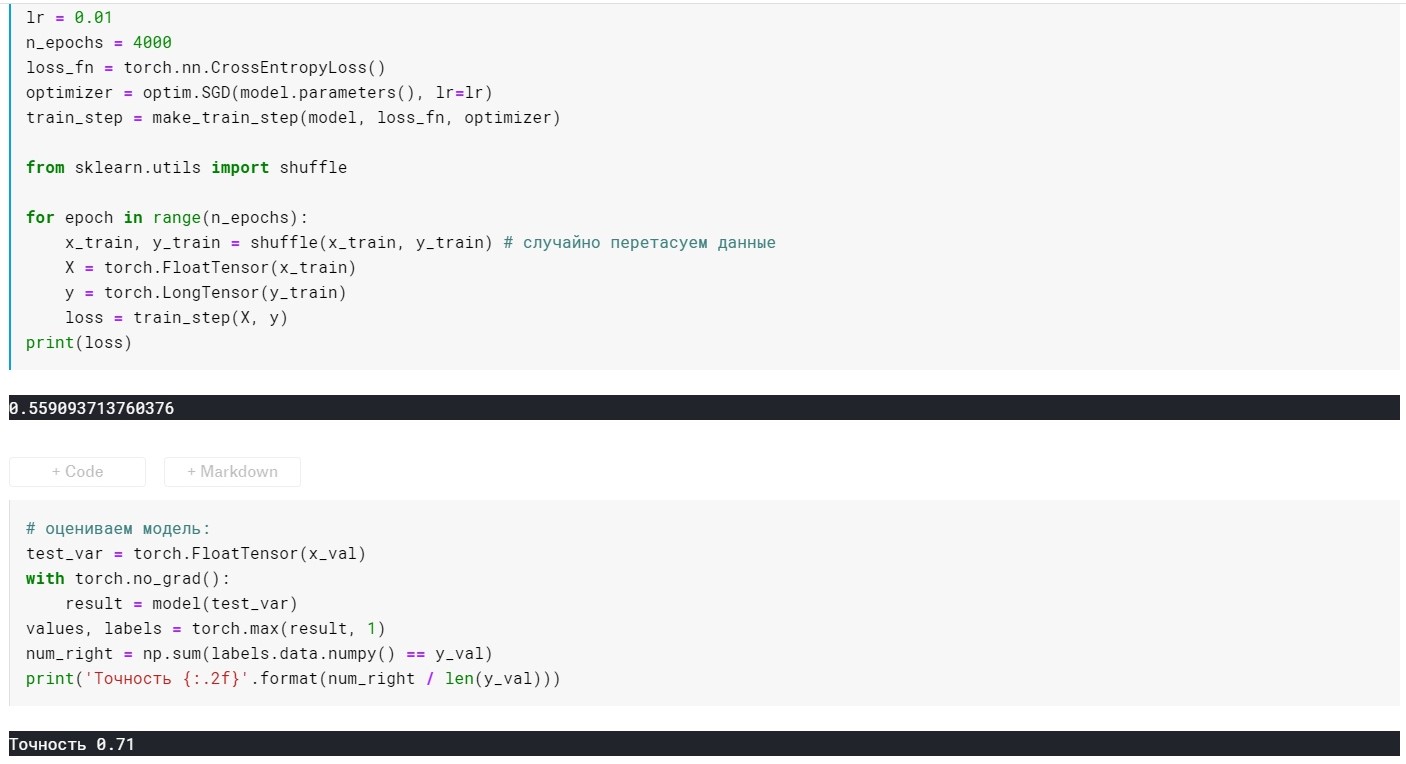
SGD mit Impulsparameter:
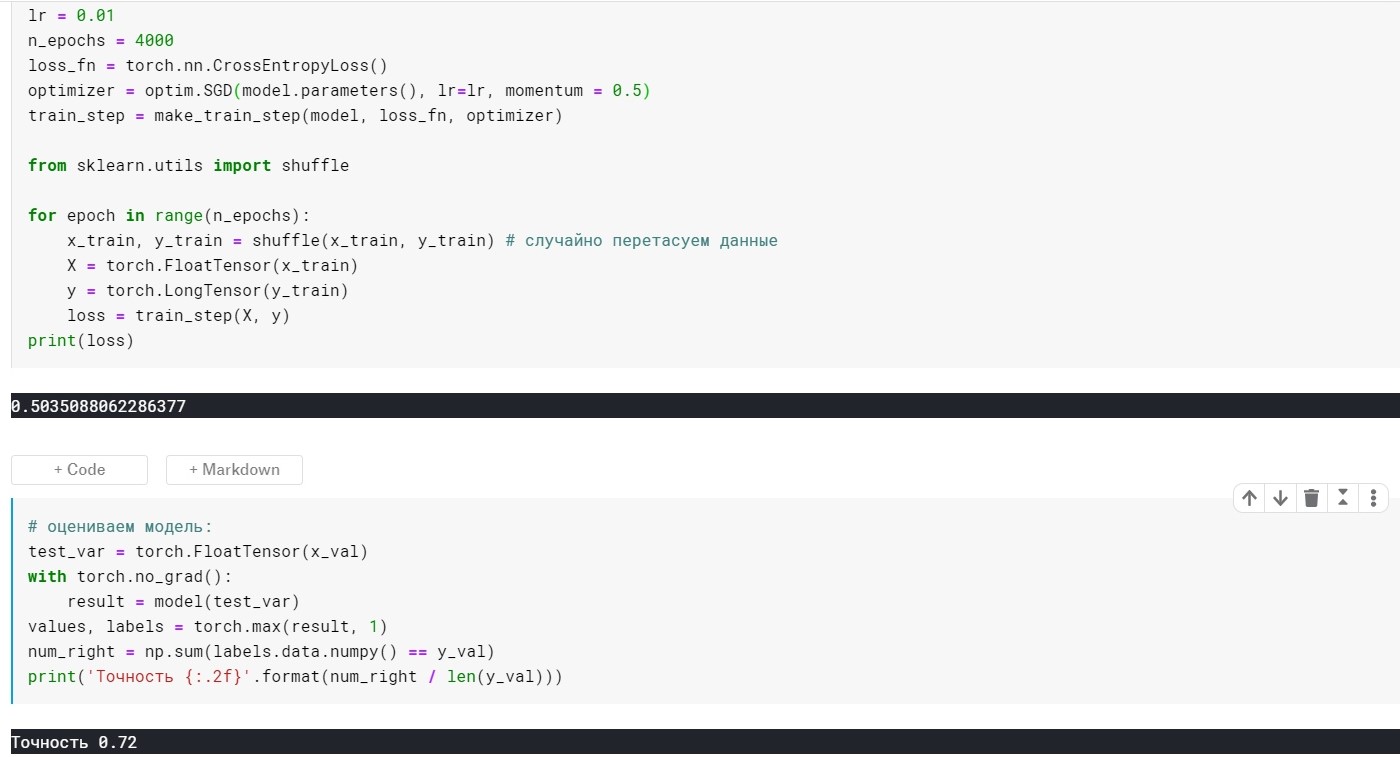
Es stellte sich nicht viel besser heraus, aber der Punkt hier ist, dass es Methoden gibt, die sofort die Ideen der Skalierung und Trägheit verwenden. Zum Beispiel Adam oder Adadelta, die jetzt gute Ergebnisse zeigen. Nun, um diese Methoden zu verstehen, denke ich, dass es notwendig ist, einige grundlegende Ideen zu verstehen, die in einfacheren Methoden verwendet werden.
Vielen Dank für Ihre Aufmerksamkeit!