Die Übersetzung des Artikels wurde speziell für Studierende der Grund- und Fortgeschrittenenkurse „Mathematik für Datenwissenschaften“ erstellt.
Der Bayes-Satz ist einer der bekanntesten Sätze in der Statistik und Wahrscheinlichkeitstheorie. Auch wenn Sie nicht mit der Berechnung quantitativer Indikatoren arbeiten, mussten Sie sich wahrscheinlich irgendwann in Vorbereitung auf die Prüfung mit diesem Theorem vertraut machen.
P (A | B) = P (B | A) · P (A) / P (B)So sieht es aus, aber was bedeutet es und wie funktioniert es? Heute werden wir es herausfinden und tief in den Satz von Bayes einsteigen.
Gründe, unser Urteil zu bestätigen
Was ist der springende Punkt der Wahrscheinlichkeitstheorie und -statistik? Eine der wichtigsten Anwendungen betrifft die Entscheidungsfindung unter Unsicherheit. Wenn Sie sich entscheiden, eine Aktion auszuführen (es sei denn, Sie sind natürlich eine vernünftige Person), wetten Sie, dass nach Abschluss dieser Aktion ein besseres Ergebnis erzielt wird, als wenn diese Aktion nicht stattgefunden hätte ... Aber Wetten ist eine Sache unzuverlässig, wie entscheiden Sie letztendlich, ob Sie diesen oder jenen Schritt machen oder nicht?
Auf die eine oder andere Weise bewerten Sie die Wahrscheinlichkeit eines erfolgreichen Ergebnisses, und wenn diese Wahrscheinlichkeit über einem bestimmten Schwellenwert liegt, machen Sie einen Schritt.
Daher ist die Fähigkeit, die Erfolgswahrscheinlichkeit genau einzuschätzen, entscheidend, um die richtigen Entscheidungen zu treffen. Trotz der Tatsache, dass Zufälligkeit immer eine Rolle für das Endergebnis spielt, sollten Sie lernen, diese Zufälligkeiten richtig zu verwenden und sie im Laufe der Zeit zu Ihrem Vorteil zu nutzen.
Hier tritt das Bayes-Theorem in Kraft - es gibt uns eine quantitative Grundlage, um unser Vertrauen in das Ergebnis der Aktion aufrechtzuerhalten, wenn sich Umweltfaktoren ändern, was es uns wiederum ermöglicht, den Entscheidungsprozess im Laufe der Zeit zu verbessern.
Lassen Sie uns die Formel analysieren
Schauen wir uns die Formel noch einmal an:
P (A | B) = P (B | A) · P (A) / P (B)Hier:
- P (A | B) - Eintrittswahrscheinlichkeit von Ereignis A, sofern Ereignis B bereits eingetreten ist;
- P (B | A) - Wahrscheinlichkeit des Auftretens von Ereignis B, vorausgesetzt, Ereignis A ist bereits eingetreten. Jetzt sieht es aus wie ein Teufelskreis, aber wir werden bald verstehen, warum die Formel funktioniert.
- P (A) - a priori (bedingungslose) Eintrittswahrscheinlichkeit von Ereignis A;
- P (B) - a priori (bedingungslose) Wahrscheinlichkeit des Auftretens von Ereignis B.
P (A | B) ist ein Beispiel für eine nachträgliche (bedingte) Wahrscheinlichkeit, dh eine, die die Wahrscheinlichkeit eines bestimmten Zustands der umgebenden Welt misst (nämlich den Zustand, in dem Ereignis B aufgetreten ist). Während P (A) ein Beispiel für eine a priori Wahrscheinlichkeit ist, die in jedem Zustand der umgebenden Welt gemessen werden kann.
Schauen wir uns als Beispiel den Satz von Bayes in Aktion an. Angenommen, Sie haben kürzlich einen Datenanalysekurs im Bootcamp abgeschlossen. Sie haben von einigen Unternehmen, in denen Sie interviewt wurden, keine Antwort erhalten und beginnen sich Sorgen zu machen. Sie möchten also die Wahrscheinlichkeit berechnen, mit der ein bestimmtes Unternehmen Ihnen ein Stellenangebot unterbreitet, sofern drei Tage vergangen sind und Sie nicht zurückgerufen wurden.
Wir schreiben die Formel anhand unseres Beispiels neu. In diesem Fall erhält Ergebnis A (
Angebot ) ein Stellenangebot, und Ergebnis B (
NoCall ) lautet „drei Tage lang kein Anruf“. Auf dieser Grundlage kann unsere Formel wie folgt umgeschrieben werden:
P ( Angebot | NoCall ) = P ( NoCall | Angebot ) * P ( Angebot ) / P ( NoCall )Der Wert von
P ( Offer | NoCall ) ist die Wahrscheinlichkeit, ein Angebot zu erhalten, sofern innerhalb von drei Tagen kein Anruf
eingeht . Diese Wahrscheinlichkeit ist äußerst schwer einzuschätzen.
Die umgekehrte Wahrscheinlichkeit
P ( NoCall | Offer ) ,
dh das Fehlen eines Telefonanrufs für drei Tage, da Sie am Ende ein Stellenangebot vom Unternehmen erhalten haben, ist es durchaus möglich, einen Wert beizulegen. In Gesprächen mit Freunden, Personalvermittlern und Beratern werden Sie feststellen, dass diese Wahrscheinlichkeit gering ist. Manchmal kann ein Unternehmen jedoch drei Tage lang schweigen, wenn es weiterhin vorhat, Sie zur Arbeit einzuladen. Sie bewerten also:
P ( NoCall | Angebot ) = 40%40% sind nicht schlecht und es scheint immer noch Hoffnung zu geben! Aber wir sind noch nicht fertig. Jetzt müssen wir
P ( Angebot ) bewerten, die Wahrscheinlichkeit, zur Arbeit zu gehen. Jeder weiß, dass die Arbeitssuche ein langer und schwieriger Prozess ist. Möglicherweise müssen Sie mehrmals ein Vorstellungsgespräch führen, bevor Sie dieses Angebot erhalten. Daher bewerten Sie:
P ( Angebot ) = 20%Jetzt müssen wir nur noch
P ( NoCall ) bewerten, die Wahrscheinlichkeit, dass Sie innerhalb von drei Tagen keinen Anruf vom Unternehmen erhalten. Es gibt viele Gründe, warum Sie möglicherweise nicht innerhalb von drei Tagen zurückgerufen werden - sie können Ihre Kandidatur ablehnen oder dennoch Interviews mit anderen Kandidaten führen, oder der Personalvermittler ist einfach krank und ruft daher nicht an. Nun, es gibt viele Gründe, warum Sie möglicherweise keinen Anruf haben. Daher bewerten Sie diese Wahrscheinlichkeit wie folgt:
P ( NoCall ) = 90%Und jetzt können wir
P ( Offer | NoCall ) berechnen:
P ( Angebot | NoCall ) = 40% * 20% / 90% = 8,9%Dies ist recht klein, daher ist es leider rationaler, diesem Unternehmen Hoffnung zu lassen (und weiterhin Lebensläufe an andere zu senden). Wenn es immer noch etwas abstrakt erscheint, machen Sie sich keine Sorgen. Mir ging es genauso, als ich zum ersten Mal von Bayes 'Satz erfuhr. Nun wollen wir sehen, wie wir zu diesen 8,9% gekommen sind (denken Sie daran, dass Ihre anfängliche Punktzahl von 20% bereits niedrig war).
Die Intuition hinter der Formel
Denken Sie daran, wir haben gesagt, dass der Bayes'sche Satz die Grundlage für die Bestätigung unserer Urteile bildet. Woher kommen sie also? Sie werden aus der a priori Wahrscheinlichkeit
P (A) abgeleitet , die in unserem Beispiel
P ( Angebot ) genannt wird. Dies ist unsere erste Beurteilung, wie wahrscheinlich es ist, dass eine Person ein Stellenangebot erhält. In unserem Beispiel können Sie davon ausgehen, dass die Wahrscheinlichkeit von vornherein die Wahrscheinlichkeit ist, dass Sie zum Zeitpunkt des Verlassens des Vorstellungsgesprächs ein Stellenangebot erhalten.
Neue Informationen werden angezeigt - 3 Tage sind vergangen, und das Unternehmen hat Sie nicht zurückgerufen. Daher verwenden wir andere Teile der Gleichung, um unsere a priori Wahrscheinlichkeit eines neuen Ereignisses anzupassen.
Schauen wir uns die Wahrscheinlichkeit
P (B | A) an , die in unserem Beispiel
P ( NoCall | Offer ) heißt . Wenn Sie den Satz von Bayes zum ersten Mal sehen, fragen Sie sich: Woher wissen Sie, wo Sie die Wahrscheinlichkeit
P (B | A) erhalten ? Wenn ich nicht weiß, wie hoch die Wahrscheinlichkeit für
P (A | B) ist , wie magisch sollte ich dann wissen, wie hoch die Wahrscheinlichkeit für
P (B | A) ist ? Ich erinnere mich an den Satz, den
Charles Munger einmal gesagt hat:
"Flip, immer Flip!"
- Charles Munger
Er meinte, wenn Sie versuchen, ein schwieriges Problem zu lösen, müssen Sie es auf den Kopf stellen und aus einem anderen Blickwinkel betrachten. Genau das macht der Satz von Bayes. Lassen Sie uns den Satz von Bayes in Bezug auf die Statistik neu formulieren, um ihn verständlicher zu machen (das habe ich hier gelernt):
Für mich sieht eine solche Aufzeichnung zum Beispiel klarer aus. Wir haben eine A-priori-Hypothese (Hypothese) - dass wir einen Job bekommen haben - und beobachtbare Fakten - Beweise (Beweise) - es gibt drei Tage lang keinen Anruf. Jetzt wollen wir die Wahrscheinlichkeit kennen, dass unsere Hypothese unter Berücksichtigung der dargestellten Fakten korrekt ist. Wie oben entschieden, haben wir eine Wahrscheinlichkeit
P (A) = 20% .
Zeit, alles auf den Kopf zu stellen! Wir verwenden
P ( Evidence | Hypothesis ) , um das Problem von der anderen Seite zu betrachten und zu fragen: "Wie wahrscheinlich ist es, dass diese Evidence-Ereignisse in einer Welt auftreten, in der unsere Hypothese wahr ist?" Wenn wir also zu unserem Beispiel zurückkehren, möchten wir wissen, wie wahrscheinlich es ist, dass wir weiterhin eingestellt werden, wenn sie uns nicht innerhalb von drei Tagen anrufen. Im obigen Bild habe ich
P ( Evidence | Hypothesis ) als „Scaler“ (Scaler) markiert, da dieses Wort die Essenz der Bedeutung gut widerspiegelt. Wenn wir es mit einem a priori-Wert multiplizieren, verringert oder erhöht es die Wahrscheinlichkeit eines Ereignisses, je nachdem, ob ein Ereignis, das unsere Hypothese beweist, „schädlich“ ist. In unserem Fall ist es weniger wahrscheinlich, dass wir zur Arbeit gerufen werden, je mehr Tage ohne Anruf vergehen. 3 Tage Schweigen sind bereits schlecht (sie reduzieren unsere a priori Wahrscheinlichkeit um 60%), während 20 Tage ohne Anruf die Hoffnung auf einen Arbeitsplatz völlig zerstören. Je mehr Beweisereignisse sich ansammeln (mehr Tage vergehen ohne Telefonanruf), desto schneller verringert der Skalierer die Wahrscheinlichkeit. Ein Skalierer ist ein Mechanismus, den der Satz von Bayes verwendet, um unser Urteilsvermögen anzupassen.
Es gibt eine Sache, mit der ich in der Originalversion dieses Artikels zu kämpfen hatte. Dies war die Formulierung, warum
P ( Evidenz | Hypothese ) leichter zu bewerten ist als P (Hypothese | Evidenz). Der Grund dafür ist, dass
P ( Evidence | Hypothesis ) ein viel begrenzterer Bereich der Beurteilung der Welt ist. Wir schränken den Umfang ein und vereinfachen die Aufgabe. Wir können eine Analogie zu Feuer und Rauch ziehen, wobei Feuer unsere Hypothese ist und die Beobachtung von Rauch ein Ereignis ist, das das Vorhandensein von Feuer beweist.
P (Feuer | Rauch) ist schwieriger zu bewerten, da viele Dinge Rauch verursachen können - Autoabgase, Fabriken, die Person, die Hamburger auf Holzkohle brät. Gleichzeitig ist
P (Rauch | Feuer) leichter zu bewerten, da in einer Welt, in der es Feuer gibt, mit ziemlicher Sicherheit Rauch vorhanden sein wird.
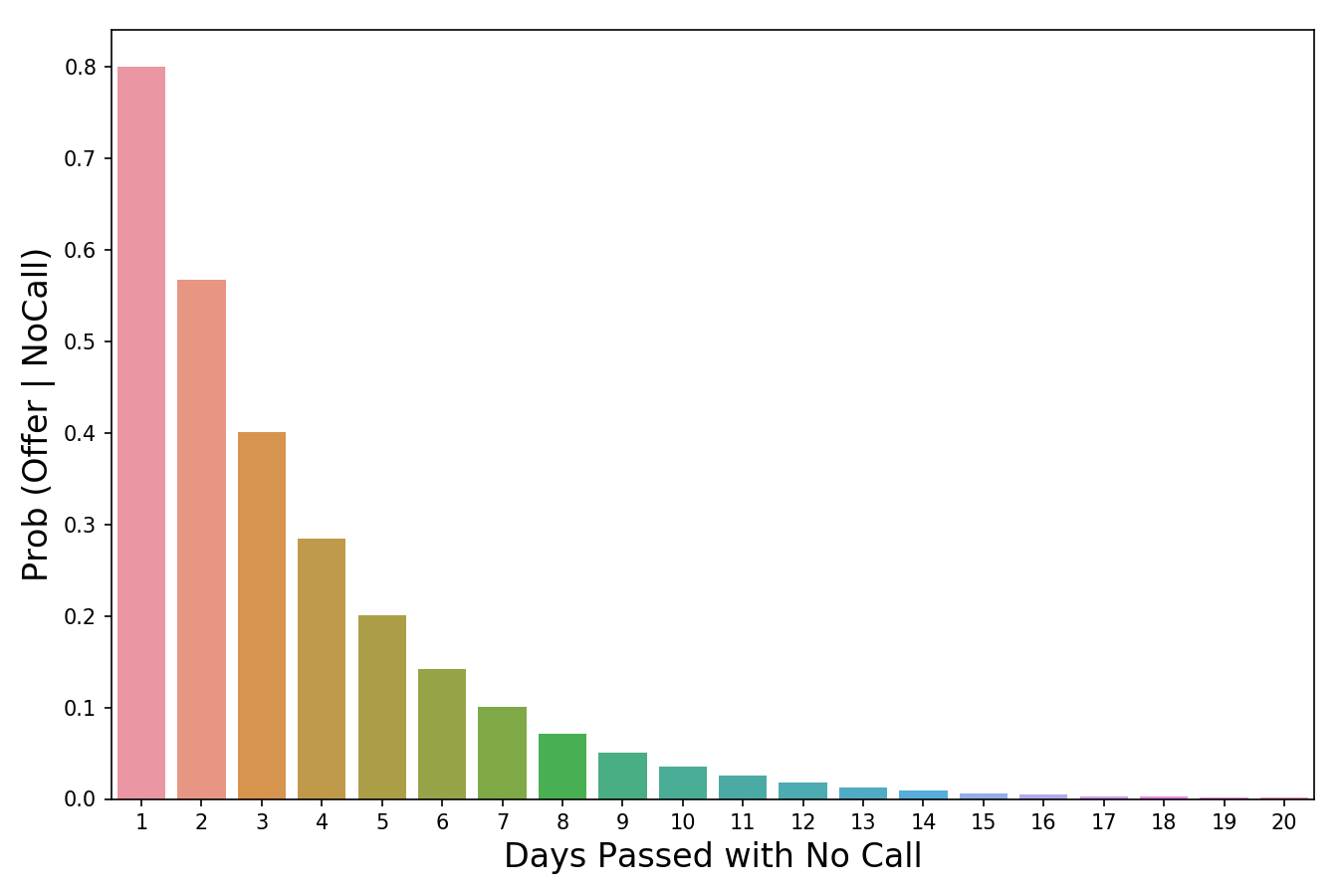Der Wahrscheinlichkeitswert nimmt ab, wenn die Anzahl der Tage ohne Anruf vergeht.Der letzte Teil der Formel,
P (B) oder
P ( Evidence ) , ist der Normalisierer. Wie der Name schon sagt, besteht sein Zweck darin, das Produkt aus a priori Wahrscheinlichkeit und Skalierer zu normalisieren. Wenn es keinen Normalisierer gäbe, hätten wir den folgenden Ausdruck:
Beachten Sie, dass das Produkt aus a priori Wahrscheinlichkeit und einem Skalierer gleich der gemeinsamen Wahrscheinlichkeit ist. Und da eine der Komponenten von
P ( Evidence ) darin enthalten ist , würde die gemeinsame Wahrscheinlichkeit durch die geringe Häufigkeit von Ereignissen beeinflusst.
Dies ist ein Problem, da die gemeinsame Wahrscheinlichkeit ein Wert ist, der alle Zustände der Welt umfasst. Aber wir brauchen nicht alle Staaten, wir brauchen nur die Staaten, die durch Ereignisse bestätigt wurden. Mit anderen Worten, wir leben in einer Welt, in der Ereignisse - Beweise bereits stattgefunden haben und deren Anzahl keine Rolle mehr spielt (daher möchten wir nicht, dass sie unsere Berechnungen im Prinzip beeinflussen). Das Teilen des Produkts von a priori Wahrscheinlichkeit und Skalierer durch
P ( Evidence ) ändert es von gemeinsamer Wahrscheinlichkeit zu bedingt (posterior). Die bedingte Wahrscheinlichkeit berücksichtigt nur die Zustände der Welt, in denen ein ereignissicherer Vorgang stattgefunden hat, und genau das erreichen wir.
Ein weiterer Gesichtspunkt, unter dem wir untersuchen können, warum wir den Skalierer in einen Normalisierer unterteilen, ist, dass sie zwei wichtige Fragen beantworten - und ihre Haltung kombiniert diese Informationen. Nehmen wir ein Beispiel aus meinem jüngsten
Bayes-Artikel . Angenommen, wir versuchen herauszufinden, ob das beobachtete Tier eine Katze ist, basierend auf einem einzigen Zeichen - Geschicklichkeit. Wir wissen nur, dass das Tier, über das wir sprechen, agil ist.
- Scaler sagt uns, wie viel Prozent der Katzen gut mit Geschicklichkeit umgehen können. Dieser Wert sollte ziemlich hoch sein, sagen wir 0,90.
- Der Normalisierer gibt an, wie viel Prozent der Tierfallen im Prinzip vorhanden sind. Dieser Wert sollte durchschnittlich sein, z. B. 0,50.
- Das Verhältnis 0,90 / 0,50 = 1,8 zeigt an, dass Sie die Wahrscheinlichkeit von vornherein ändern müssen, denn wenn Sie zuvor anders gedacht haben, ist es Zeit, Ihre Meinung zu ändern, da Sie höchstwahrscheinlich mit einer Katze zu tun haben. Der Grund, warum dies in Betracht gezogen werden kann, ist, dass wir einige Beweise dafür beobachtet haben, dass das Tier agil ist. Dann fanden wir heraus, dass der Anteil an geschickten Katzen größer ist als der Anteil an geschickten Tieren im Allgemeinen. In Anbetracht dessen, dass wir im Moment nur ein solches Beweisstück kennen und nichts weiter, wäre es ratsam, unsere Überzeugungen in Richtung der Gedanken zu überdenken, dass wir immer noch eine Katze beobachten.
Zusammenfassend
Jetzt, da wir wissen, wie jeder Teil der Formel zu interpretieren ist, können wir endlich alles zusammenfügen und uns ansehen, was passiert ist:
- Unmittelbar nach dem Vorstellungsgespräch legen wir eine a priori Wahrscheinlichkeit fest - die Wahrscheinlichkeit, dass wir eingestellt werden, beträgt 20%.
- Je mehr Tage ohne Anruf vergehen, desto unwahrscheinlicher ist es, dass wir eingestellt werden. Zum Beispiel glauben wir nach drei Tagen ohne Anruf, dass in einer Welt, in der wir diesen Job bekommen können, nur eine 40% ige Chance besteht, dass das Unternehmen so lange zieht, bevor es Sie anruft. Multiplizieren Sie den Scaler mit einer Wahrscheinlichkeit von vornherein und erhalten Sie 20% * 40% = 8%
- Schließlich verstehen wir, dass 8% für alle Bedingungen berechnet wurden, unter denen sich die Welt befinden kann. Wir sind jedoch nur besorgt über Bedingungen, unter denen wir seit drei Tagen nicht mehr angerufen wurden. Um nur mit diesen Bedingungen zu arbeiten, nehmen wir für 90% die a priori Wahrscheinlichkeit, dass innerhalb von drei Tagen kein Anruf eingeht und wir einen Normalisierer erhalten. Wir teilen die zuvor erhaltenen 8% durch den Normalisierer 8% / 90% = 8,9% und erhalten die endgültige Antwort. Wenn Sie unter allen Bedingungen der Welt innerhalb von drei Tagen keinen Anruf vom Unternehmen erhalten haben, beträgt die Wahrscheinlichkeit, einen Job zu bekommen, insgesamt nur 8,9%.
Ich hoffe, dieser Artikel hat Ihnen geholfen!