VK hat eine Gruppe mit folgender Beschreibung:

Das gleiche Foto wird jeden Tag manuell auf einem Computer gespeichert und erneut hochgeladen, wodurch die Qualität allmählich abnimmt.

Links ist das Originalbild, das am 7. Juni 2012 hochgeladen wurde, rechts ist es das, was es jetzt ist.

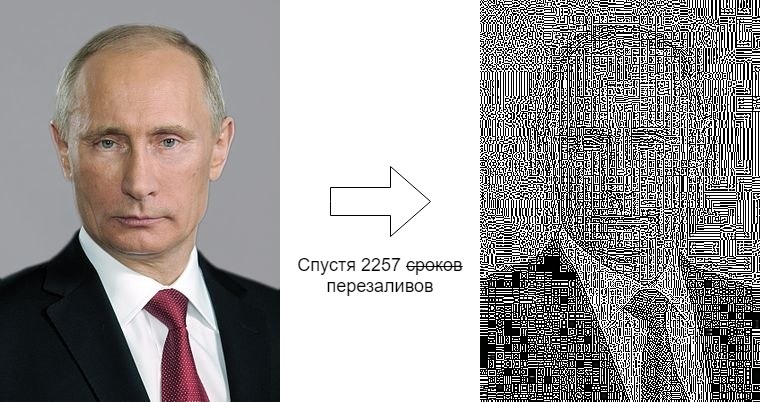
Dieser Unterschied ist sehr verdächtig. Versuchen wir herauszufinden, was in diesen 7 Jahren passiert ist. Zur Bekanntschaft gibt es auf Medusa einen Artikel über diese Gruppe, aber nur die technische Seite wird uns interessieren.

Warum und zu welchem ​​Zeitpunkt komprimiert JPEG mit Verlusten

Betrachten Sie ein stark vereinfachtes JPEG-Codierungs- und Decodierungsschema. Es werden nur die Operationen gezeigt, die die Grundprinzipien des JPEG-Algorithmus veranschaulichen.

Also 4 Operationen:

• DCT ist eine diskrete Cosinustransformation.
• Quantisierung - Rundung jedes Werts auf das nächste Vielfache des Quantisierungsschritts: y = [x / h] * h, wobei h der Schritt ist.
• IDCT ist die inverse diskrete Cosinustransformation.
• Rundung ist normale Rundung. Diese Phase konnte im Diagramm nicht dargestellt werden, da dies offensichtlich ist. Aber dann wird seine Bedeutung demonstriert.

Die grüne Farbe zeigt Operationen an, bei denen alle Informationen gespeichert werden (ohne Verluste bei der Arbeit mit Gleitkommazahlen zu berücksichtigen), die rosa verlieren. Das heißt, Verluste und Artefakte treten nicht aufgrund der Kosinustransformation auf, sondern aufgrund der einfachen Quantisierung. Der Artikel wird keine wichtige Phase berücksichtigen - die Huffman-Codierung, da sie ohne Verlust ausgeführt wird.

Betrachten Sie diese Schritte genauer.

DCT

Da es für alle Fälle verschiedene DCT-Varianten gibt, möchte ich klarstellen, dass JPEG einen zweiten DCT-Typ mit Normalisierung verwendet. Bei der Codierung wird jedes Bild in 8 x 8 Quadrate (für jeden Kanal) unterteilt. Jedes solche Quadrat kann als 64-dimensionaler Vektor dargestellt werden. Die Kosinustransformation besteht darin, die Koordinaten dieses Vektors auf einer anderen orthonormalen Basis zu finden. Es ist schwierig, den 64-dimensionalen Raum zu visualisieren, daher werden im Folgenden zweidimensionale Analogien angegeben. Sie können sich vorstellen, dass das Bild in 2x1 Blöcke unterteilt ist. In den unten gezeigten Diagrammen entspricht die x-Achse den Werten des ersten Pixels des Blocks, die y-Achse dem zweiten.

Wenn Sie die Analogie mit einem bestimmten Beispiel fortsetzen, nehmen Sie an, dass die Werte von zwei Pixeln aus dem Originalbild 3 und 4 sind. Zeichnen Sie den Vektor (3, 4) auf der Originalbasis, wie in der folgenden Abbildung gezeigt. Die ursprüngliche Basis ist blau markiert. Die Koordinaten des Vektors in einer neuen Basis sind (4.8, 1.4).

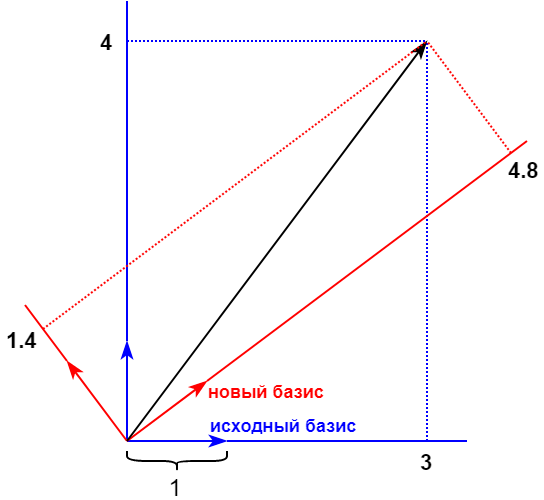
Im betrachteten Beispiel wurde zufällig eine neue Basis ausgewählt. DCT bietet eine sehr spezifische 64-dimensionale feste Basis. Die Begründung, warum es in JPEG verwendet wird, ist sehr interessant und wurde von mir in einem anderen Artikel beschrieben . Wir werden nur auf das Wesentliche eingehen. Im Allgemeinen sind die Werte aller Pixel äquivalent. Wenn wir sie jedoch mit DCT konvertieren, können wir aus den resultierenden 64 Koordinaten auf einer neuen Basis (als DCT-Transformationskoeffizienten bezeichnet) einige von ihnen mit minimalen Verlusten sicher auf Null setzen oder grob abrunden. Dies ist dank der Funktionen komprimierbarer Bilder möglich.

Quantisierung

Bruchwerte können nicht in einer Datei gespeichert werden. Daher werden abhängig vom Quantisierungsschritt die Werte 4.8, 1.4 wie folgt gespeichert:

• in Schritt 1 (die sanfteste Option): 5 und 1,
• in Schritt 2: 4 und 2
• in Schritt 3: 6 und 0.

Normalerweise wird der Schritt für jeden Wert unterschiedlich gewählt. Eine JPEG-Datei verfügt über mindestens ein Array, eine sogenannte Quantisierungstabelle, in der 64 Quantisierungsschritte gespeichert sind. Diese Tabelle hängt von der in einem Grafikeditor festgelegten Komprimierungsqualität ab.

IDCT

Wie DCT, jedoch transponiert. Mathematisch ist x = IDCT (DCT (x)). Wenn es also keine Quantisierung gäbe, wäre es möglich, sich ohne Verlust zu erholen. Aber es würde keine Komprimierung geben. Aufgrund der Verwendung der Quantisierung kann der ursprüngliche Vektor nicht immer genau berechnet werden. Die folgende Abbildung zeigt 2 Beispiele mit genauer und ungenauer Wiederherstellung. Das schräge Gitter entspricht einer neuen Basis, die gerade Linie der ursprünglichen.

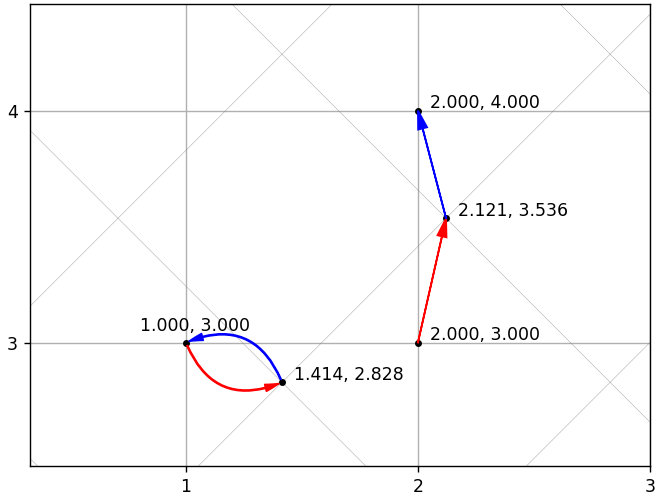
Die offensichtliche Frage stellt sich: Kann eine Sequenz der Transcodierung zu einem Vektor führen, der sich stark vom Original unterscheidet? Vielleicht.

Es wäre interessant, alle ganzzahligen Vektoren zu sortieren und zu sehen, wozu ihre Transcodierung führen wird. Um das Informationsrauschen zu reduzieren, entfernen wir das Gitter der Anfangsbasis und verbinden die ursprünglichen und rekonstruierten Vektoren (ohne Zwischenschritt) direkt durch Segmente. Betrachten Sie zunächst einen Quantisierungsschritt gleich 1 für alle Koordinaten. Die neue Basis in der folgenden Abbildung ist um 45 Grad gedreht, und dafür haben wir 17,1% der ungenauen Wiederherstellungen. Die Farben der Segmente bedeuten nichts, aber sie sind nützlich, um ihre visuelle Verschmelzung zu verhindern.

Diese Basis ist 10,3 Grad mit 7,4% ungenauen Wiederfindungsraten:

In der Nähe:

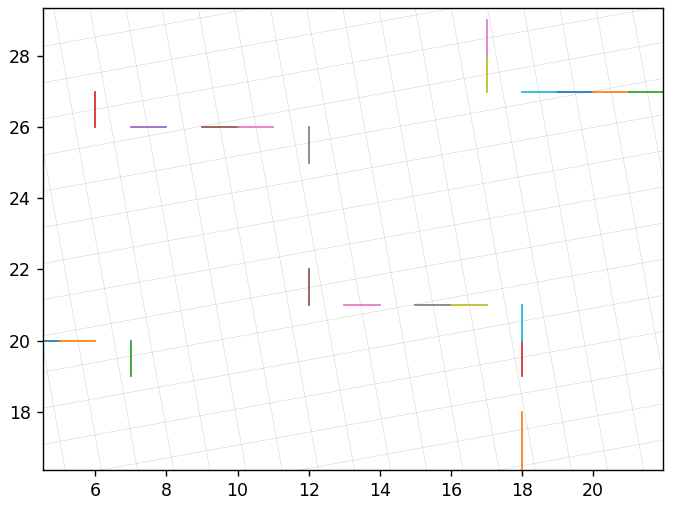
Und dieser liegt bei 10,4 von 6,4%:

19 Grad von 12,5%:

Wenn Sie jedoch den Quantisierungsschritt größer als 1 einstellen, konzentrieren sich die rekonstruierten Vektoren deutlich in der Nähe der Gitterknoten. Dies ist Schritt 5:

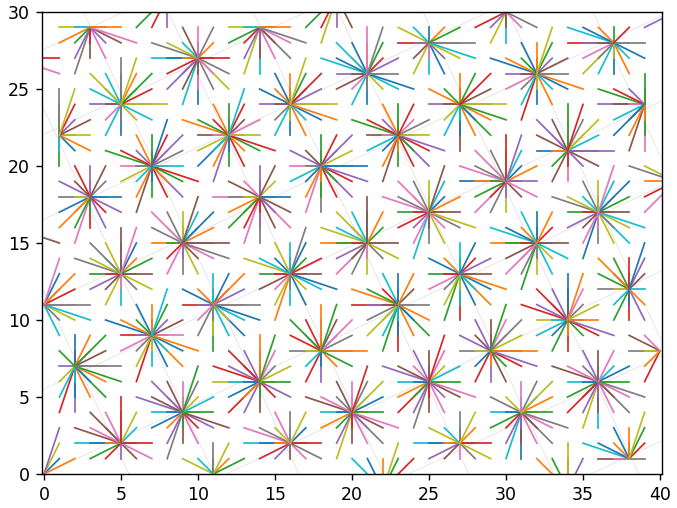
Dies ist 2:

Wenn Sie das Bild mehrmals, jedoch mit derselben Tonhöhe, neu codieren, geschieht im Vergleich zu einer einzelnen Neukodierung fast nichts. Die Werte scheinen in den Knoten des Gitters "stecken zu bleiben" und können von dort nicht mehr zu anderen Knoten "springen". Wenn der Schritt anders ist, „springt“ der Vektor von einem Gitterknoten zum anderen. Das kann ihn überall hin bringen. Die folgende Abbildung zeigt das Ergebnis von 4 Transcodierungen mit den Schritten 1, 2, 3, 4. Mit Schritt 12 sehen Sie ein großes Raster. Dieser Wert ist das kleinste gemeinsame Vielfache von 1, 2, 3, 4.

Und dazu - mit Schritten von 1 bis 7. Die Visualisierung wird nur für einen Teil der ursprünglichen Vektoren angezeigt, um die Visualisierung zu verbessern.

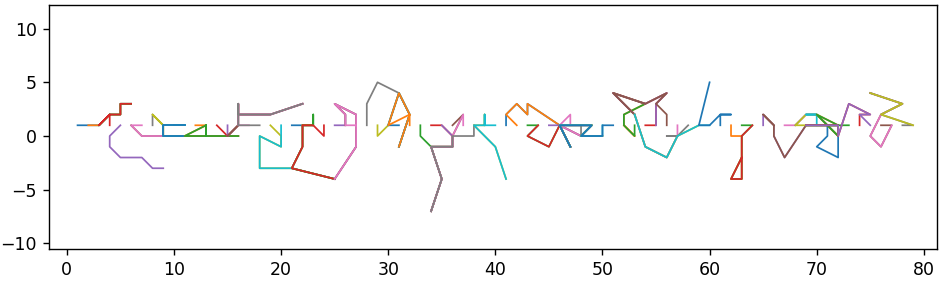
Rundung

Warum Werte nach IDCT abrunden? Wenn Sie diese Phase loswerden, wird das wiederhergestellte Bild durch Bruchwerte dargestellt, und wir verlieren beim Neucodieren nichts. Aus mathematischer Sicht werden wir einfach ohne Verlust von einer Basis zur anderen wechseln. Hier ist die Umwandlung von Farbräumen zu erwähnen. Obwohl JPEG den Farbraum nicht reguliert und es Ihnen ermöglicht, direkt im Quell-RGB zu speichern, wird in den allermeisten Fällen die vorläufige Konvertierung in YCbCr verwendet. Augenmerkmale und all das. Und eine solche Umwandlung führt auch zu Verlusten.

Angenommen, wir erhalten eine JPEG-Datei, die mit maximaler Qualität komprimiert ist, dh mit einem Quantisierungsschritt von 1 für alle Koeffizienten. Wir wissen nicht, welcher Codec verwendet wurde, aber normalerweise führen Codecs nach der RGB -> YCbCr-Konvertierung eine Rundung durch. Da die Qualität maximal ist, erhalten wir nach IDCT gebrochene, aber ziemlich nahe an den ursprünglichen Werten im YCbCr-Raum liegende Werte. Wenn wir runden, werden die meisten von ihnen genau wiederhergestellt.

Wenn sie jedoch nicht gerundet sind, kann die YCbCr -> RGB-Konvertierung sie aufgrund der geringen Unterschiede noch weiter von den ursprünglichen Werten entfernen. Mit der anschließenden Transcodierung wird die Lücke immer größer. Um diesen Prozess irgendwie zu visualisieren, verwenden wir die Hauptkomponentenmethode, um 64-dimensionale Vektoren auf eine Ebene zu projizieren. Dann erhalten wir für 1000 Transcodes ungefähr die folgende Folge von Änderungen:

Die absoluten Werte der Achsen sind hier nicht sehr sinnvoll, aber die relative Bedeutung der Verzerrungen kann verwendet werden.

Beispiele für mehrere Transcodierungen

Quellkatze:

Nach einer Konservierung mit Qualität 50:

Nach einer nachfolgenden Anzahl von Transcodes mit derselben Qualität ändert sich das Bild nicht. Jetzt werden wir die Qualität schrittweise von 90 auf 50 in 1 reduzieren:

In der folgenden Tabelle ist ungefähr dasselbe passiert:

Nach einer Konservierung mit Qualität 20:

Nahtlos von 90 bis 20:

Jetzt 1000 mal mit zufälliger Qualität von 80 bis 90:

10.000 Mal:

VK Group Bilderanalyse

Beginnen wir mit der Analyse von mehr als 2000 Bildern aus der VK-Gruppe. Überprüfen Sie zunächst die durchschnittliche absolute Abweichung vom ersten. Die x-Achse ist die Bildnummer (oder der Tag), die y-Achse ist die Abweichung.

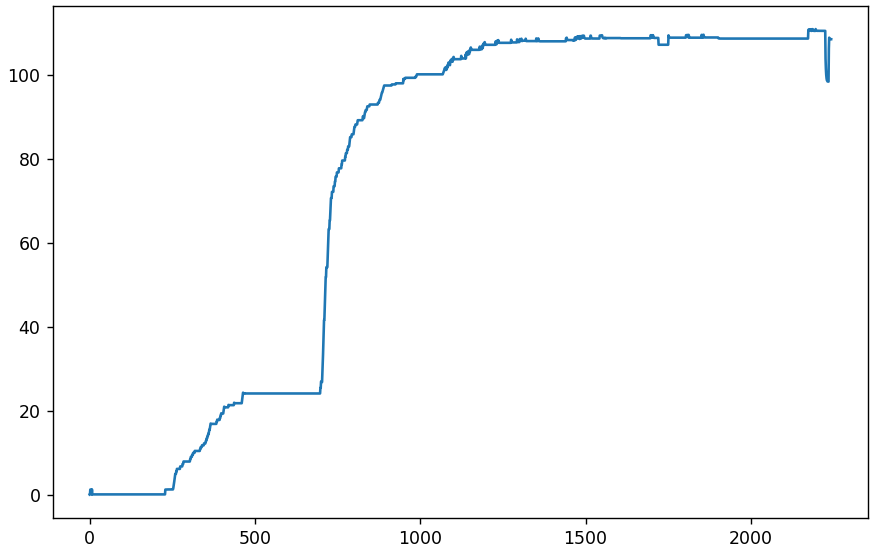
Fahren wir mit dem Differentialdiagramm fort, das die durchschnittliche absolute Abweichung der benachbarten Bilder zeigt.

Kleine Schwankungen am Anfang sind normal. Bis zum 232. läuft alles gut, die Bilder sind völlig identisch. Und der 233. unterscheidet sich plötzlich um durchschnittlich 1,23 für jedes Pixel (auf einer Skala von 0 bis 255). Das ist viel. Vielleicht haben sich die Quantisierungstabellen gerade geändert. Schau es dir an. Gleichzeitig ist es mit der Größe der empfangenen Dateien vergleichbar.

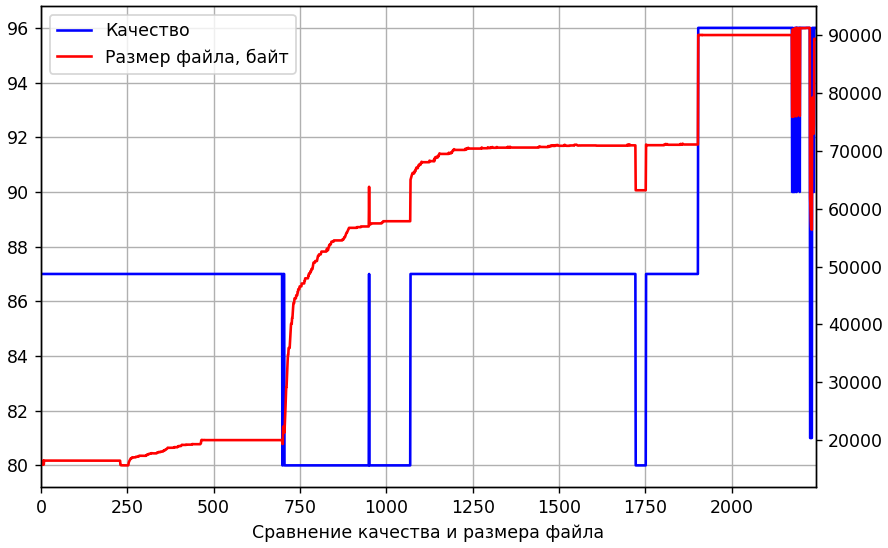
Ja, die Tabellen haben sich geändert. Aber nicht früher als in den 700ern. Dann trat möglicherweise eine versteckte Zwischen-Transcodierung mit geringer Qualität auf. Versuchen wir, den 232. zweimal neu zu codieren. Zum ersten Mal werden wir verschiedene Qualitätsstufen durchlaufen, und zum zweiten Mal verwenden wir dieselbe Quantisierungstabelle wie für alle vom 1. bis zum 700er. Unser Ziel ist es, das Bild so ähnlich wie möglich zum 233. zu machen. In der folgenden Abbildung ist entlang der x-Achse die Qualität der Zwischentranscodierung angegeben, entlang y ist die durchschnittliche absolute Abweichung von der 233 ..

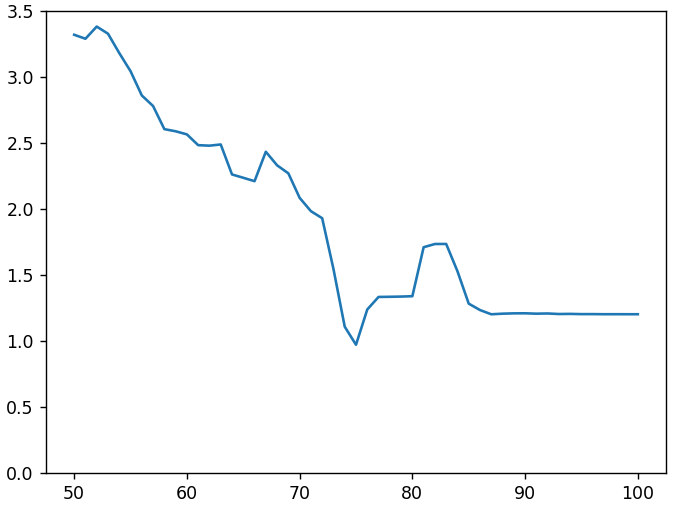
Es gibt zwar einen Fehler im Diagramm mit einer Qualität von 75%, ungefähr gleich 1, aber immer noch weit von der gewünschten Null entfernt. Das Hinzufügen der 2. Zwischenstufe und das Ändern der Parameter der Unterabtastung verbesserte die Situation nicht.

Bei den restlichen Bildern ist alles ungefähr gleich, und die Änderung in den Quantisierungstabellen wird ebenfalls überlagert. Das heißt, irgendwann ändert sich das Bild dramatisch, dann stabilisiert es sich in wenigen Tagen, aber nur bis ein neuer Anstieg auftritt. Möglicherweise ändert sich das Image selbst auf den Servern. Ich kann die Beteiligung des Gruppenadministrators nicht vollständig ausschließen.

Leider habe ich nicht herausgefunden, was wirklich mit dem Bild passiert ist. Zumindest bin ich mir jetzt sicher, dass es nicht nur eine Erhaltung war. Vor allem aber wurde es besser, die laufenden Prozesse während des Codierens und Decodierens darzustellen. Hoffe du auch.

Archiv mit Bildern für unabhängige Recherchen.