Splines in 3D-Grafiken, die am meisten automatisierte Option

Vor ungefähr einem Monat begann ich Python aus dem Dawson-Buch zu lernen und wachte tief auf, als ich mein Spiel unter Pygame schrieb. TK war so, dass es am vielversprechendsten schien, ein Spiel mit pseudo-dreidimensionalen Grafiken zu erstellen, indem die gespeicherten Oberflächen von 3D-Splines in Sprites gestopft wurden. Ich werde über Letzteres schreiben.

Es gibt also Polygone (es ist am einfachsten, mit Vierecken zu arbeiten), auf denen wir kubische Flächen so strecken möchten, dass sie reibungslos zusammenpassen - diese Flächen sind Splines.



Am bequemsten ist es, einen Spline für ein Polygon als Funktion darzustellen

$$

$$g (u, v) = v \ cdot g_1 (u) + (1 - v) \ cdot g_2 (u) + u \ cdot g_3 (v) + (1-u) \ cdot g_4 (v) (1)$$

Hier

$$

$$g_1, g_2, g_3, g_4$$

- kubische Polynome, die einige Randbedingungen erfüllen (in der folgenden Abbildung - hellgrüne und rote Kurven und abgeleitete Anfangsbedingungen - lila und blaue Vektoren); u und v variieren von 0 bis 1.



Bei dieser Interpretation gehen einige Grade verloren (Produkte von 2 und 3 Grad von Parametern), aber die Polynomkoeffizienten können gefunden werden, indem nur 12 Vektoren der Anfangsbedingungen angegeben werden (4 Polygonpunkte und Ableitungsvektoren in Bezug auf u und v für jeden Punkt). An den Verbindungsstellen fallen Splines zusammen, wenn ähnliche Anfangsbedingungen für benachbarte Polygone festgelegt werden (die Ableitungsvektoren müssen kollinear sein, die Oberfläche verläuft durch dieselben Punkte des Polygons).

Ein Problem - die Ableitung mit einer solchen Erklärung des Problems an der gesamten Grenze kann nicht zusammenfallen - es wird kleine Artefakte an den Kreuzungen geben. Sie können sich 4 weitere Bedingungen ausdenken, um dies zu korrigieren, und der Formel sorgfältig einen weiteren Begriff hinzufügen

$$

$$u \ cdot v \ cdot (u-1) \ cdot (v-1) \ cdot g_5 (u, v)$$

Das verdirbt nicht die Grenzen, aber dies ist ein Thema für einen separaten Artikel.

Eine Alternative ist die Bezier-Oberfläche , aber sie schlägt vor, 16 Parameter von unverständlicher (für mich) mathematischer Bedeutung einzustellen, d. H. Es wird davon ausgegangen, dass der Künstler mit seinen eigenen Händen arbeitet. Das ist für mich nicht sehr geeignet, daher folgt ein Fahrrad mit Krücken.

Die Koeffizienten (1) lassen sich am einfachsten berechnen, indem die inverse Matrix zur Matrix der Werte und Ableitungen in den Ecken ermittelt und mit den Eingabebedingungen multipliziert wird (dreimal für jede Koordinate). Die Matrix kann folgende sein:


NumPy leistet hier hervorragende Arbeit.

Eine Frage bleibt - woher die Vektoren der Derivate kommen. Es wird angenommen, dass sie irgendwie basierend auf der Position benachbarter (für das Polygon) Punkte und aus Gründen der Glätte ausgewählt werden müssen.
Für mich persönlich war es immer noch völlig uninteressant, mit der Länge des abgeleiteten Vektors umzugehen. Die Richtung ist verständlich, aber die Länge?

Als Ergebnis wurde der folgende Algorithmus geboren:

1. In der ersten Phase erfolgt eine gewisse Klassifizierung von Punkten. In der Grafik (welche Punkte der Polygone und ihre Verbindungen angeben) werden Zyklen der Länge 4 gesucht und gespeichert, und zusätzlich werden Nachbarn aufgezeichnet, die für die Rolle der Erweiterung der Kanten des Polygons am besten geeignet sind (es wird im Voraus bestimmt, welche Kanten einer Änderung des Parameters u entsprechen und welche v entsprechen). Hier ist ein Code, der Nachbarn nach dem 0. Punkt eines Zyklus sucht, sortiert und speichert:


Ferner wird beim Konstruieren des Splines die Ableitung entlang der Kante (zum Beispiel in Bezug auf den Parameter u) am Punkt des Polygons basierend auf der Position von zwei Punkten der Kante und einem benachbarten Punkt ausgewählt (sei es die Punkte vec1, vec2 und vec3; der Punkt, an dem die Ableitung gesucht wird, ist der zweite).



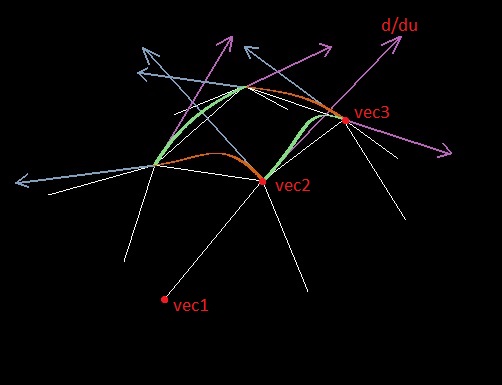
Zuerst habe ich versucht, den normalisierten Vektor vec3 - vec1 (wie ich den Lagrange-Satz angewendet habe) für diese Rolle zu verwenden, aber Probleme traten genau bei der Länge des abgeleiteten Vektors auf - es war eine schlechte Idee, ihn zu einer Konstanten zu machen.

Lyrischer Exkurs:

Um eine kleine Darstellung des Ableitungsvektors in der parametrischen Version zu erhalten, wenden wir uns einer einfachen zweidimensionalen Analogie zu - hier ein Stück eines Kreisbogens:

$$

$$g (u) = (Rsin (u \ pi / 2), Rcos (u \ pi / 2))$$

$$

$$g '(u) = (R \ pi / 2 \ cdot cos (u \ pi / 2), -R \ pi / 2 \ cdot sin (u \ pi / 2))$$

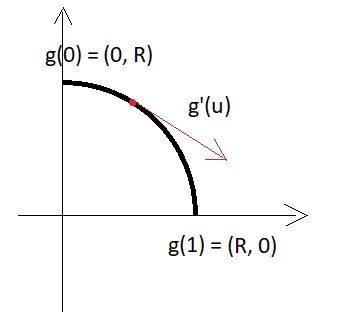
Das heißt, Der Ableitungsmodul = R * pi / 2 und hängt im Allgemeinen von der Größe des Bogenstücks ab, das wir über den Parameter einstellen.

Was tun jetzt damit? Leo Nikolaevich Tolstoy hat uns hinterlassen, dass alles rund = gut ist. Wenn wir also die Ableitung auf einen Punkt setzen, als ob wir dort einen Bogen bauen möchten, erhalten wir eine glatte, schöne Kurve.

Das Ende des Exkurses.

Die zweite Stufe der abgeleiteten Suche:

2. Durch unsere drei Punkte vec1, vec2, vec3 bauen wir eine Ebene, in dieser Ebene suchen wir nach einem Kreis, der durch alle drei Punkte verläuft. Die gewünschte Ableitung wird entlang der Tangente an den Kreis am Punkt vec2 gerichtet, und der Modul des Vektors der Ableitung sollte gleich dem Produkt aus dem Radius des Kreises und dem Winkel des Sektors sein, die zwei Punkte der Polygonfläche bilden (ähnlich unserer einfachen flachen Analogie aus dem lyrischen Exkurs).

$$

$$g '= R \ cdot \ phi$$

Alles scheint einfach zu sein, hier ist zum Beispiel der Funktionscode (NumPy wird wieder verwendet):


Nun, im Allgemeinen funktioniert alles irgendwie. Zur Demonstration nahm ich einen 5x5x5 Würfel und änderte die Position der Punkte mit einem Zufallsgenerator: