In Gamedev müssen Sie häufig etwas an ein zufälliges Haus binden: Unity hat dafür einen eigenen Zufall, und System.Random existiert parallel dazu. Es war einmal bei einem der Projekte, als ob beide unterschiedlich funktionieren könnten (obwohl sie eine gleichmäßige Verteilung haben sollten).
Dann gingen sie nicht ins Detail - es war genug, dass der Übergang zu System.Random alle Probleme behebte. Jetzt haben wir uns entschlossen, genauer zu verstehen und ein wenig zu recherchieren: wie „voreingenommen“ oder vorhersehbar RNGs sind und welche wir wählen sollen. Außerdem habe ich oft widersprüchliche Meinungen über ihre "Ehrlichkeit" gehört - versuchen wir herauszufinden, wie sich die tatsächlichen Ergebnisse auf die angegebenen beziehen.
Ein kurzes Bildungsprogramm oder RNG ist eigentlich ein PRNG
Wenn Sie bereits mit Zufallszahlengeneratoren vertraut sind, können Sie sofort mit dem Abschnitt "Testen" fortfahren.Zufallszahlen (MF) sind eine Folge von Zahlen, die mit einem zufälligen (chaotischen) Prozess, einer Entropiequelle, erzeugt werden. Das heißt, dies ist eine solche Sequenz, deren Elemente durch kein mathematisches Gesetz verbunden sind - sie haben keinen kausalen Zusammenhang.
Was einen Mitteltonbereich erzeugt, wird als Zufallszahlengenerator (RNG) bezeichnet. Es scheint, dass alles elementar ist, aber wenn wir von der Theorie zur Praxis übergehen, ist die Implementierung eines Softwarealgorithmus zur Erzeugung einer solchen Sequenz nicht so einfach.
Der Grund liegt in der Abwesenheit der Zufälligkeit in der modernen Unterhaltungselektronik. Ohne sie hören Zufallszahlen auf, zufällig zu sein, und ihr Generator wird zu einer gewöhnlichen Funktion absichtlich bestimmter Argumente. Für eine Reihe von Fachgebieten im IT-Bereich ist dies ein ernstes Problem (z. B. für die Kryptografie), für den Rest gibt es eine durchaus akzeptable Lösung.
Wir müssen einen Algorithmus schreiben, der zurückgibt, auch wenn es sich nicht wirklich um Zufallszahlen handelt, sondern ihnen so nahe wie möglich kommt - die sogenannten Pseudozufallszahlen (PSNs). Der Algorithmus wird in diesem Fall als Pseudozufallszahlengenerator (PRNG) bezeichnet.
Es gibt verschiedene Optionen zum Erstellen eines PRNG, aber für alle ist Folgendes relevant:
- Die Notwendigkeit einer Vorinitialisierung.
Dem PRNG fehlt eine Entropiequelle, daher muss vor seiner Verwendung der Ausgangszustand angegeben werden. Es wird als Zahl (oder Vektor) angegeben und als Startwert (Startwert, zufälliger Startwert) bezeichnet. Oft wird ein Prozessortaktzähler oder das numerische Äquivalent der Systemzeit als Startwert verwendet. - Reproduzierbarkeit der Sequenz.
Das PRNG ist vollständig deterministisch, sodass der während der Initialisierung angegebene Startwert eindeutig die gesamte zukünftige Zahlenfolge bestimmt. Dies bedeutet, dass ein einzelner PRSP, der mit demselben Startwert (zu unterschiedlichen Zeiten, in unterschiedlichen Programmen, auf unterschiedlichen Geräten) initialisiert wurde, dieselbe Sequenz generiert.
Sie müssen auch die Wahrscheinlichkeitsverteilung kennen, die das PRNG kennzeichnet - welche Zahlen es mit welcher Wahrscheinlichkeit generiert. Meistens ist dies entweder eine Normalverteilung oder eine Gleichverteilung.
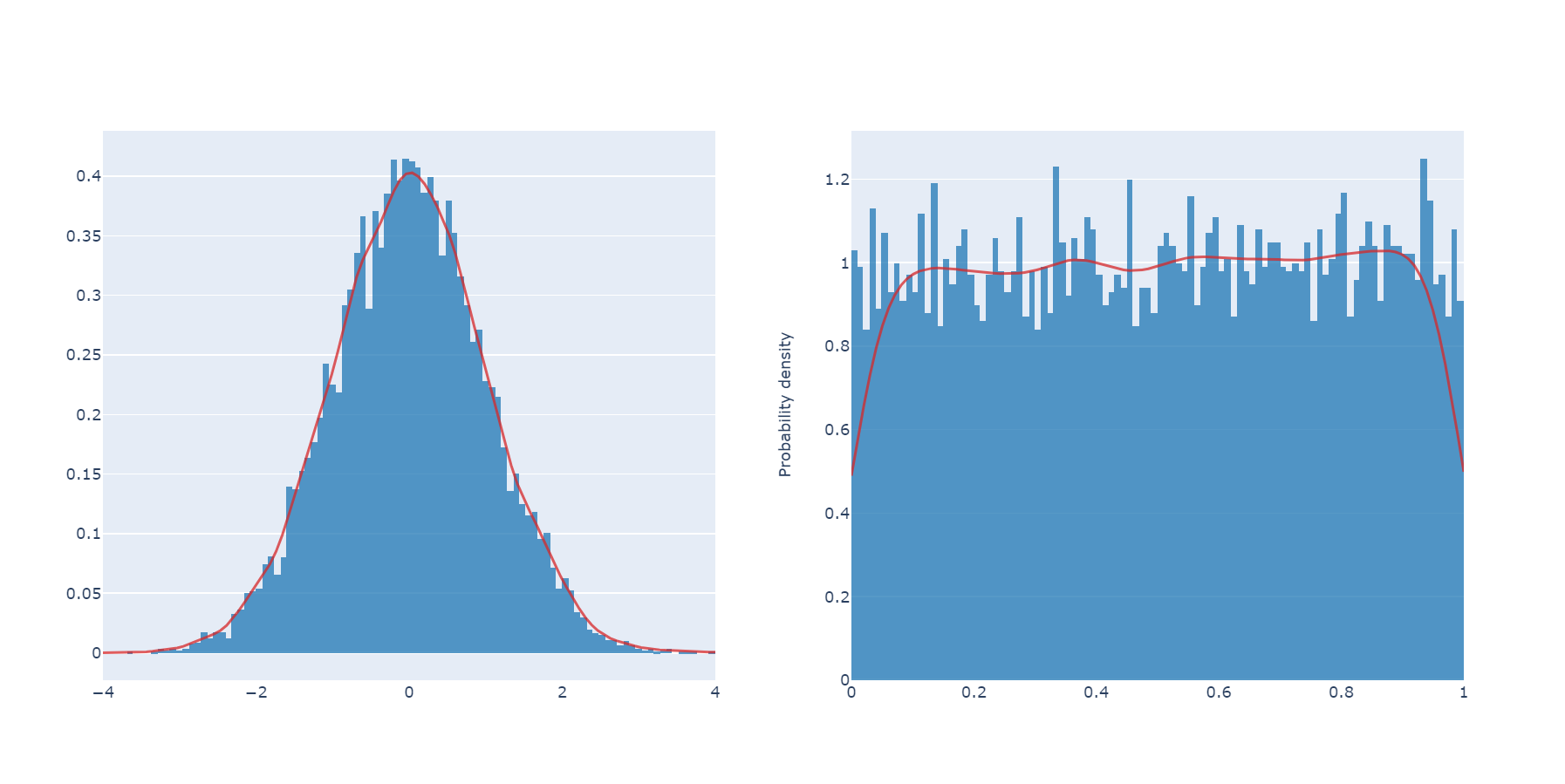Normalverteilung (links) und Gleichverteilung (rechts)Nehmen wir an, wir haben einen ehrlichen Würfel mit 24 Gesichtern. Wenn Sie es fallen lassen, beträgt die Wahrscheinlichkeit, dass eine Einheit herausfällt, 1/24 (sowie die Wahrscheinlichkeit, dass eine andere Zahl herausfällt). Wenn Sie viele Würfe ausführen und die Ergebnisse aufzeichnen, werden Sie feststellen, dass alle Gesichter ungefähr mit der gleichen Häufigkeit herausfallen. Tatsächlich kann dieser Würfel als RNG mit einer gleichmäßigen Verteilung betrachtet werden.
Und wenn Sie sofort 10 solcher Knochen werfen und die Gesamtpunktzahl zählen? Wird die Einheitlichkeit für sie gewahrt bleiben? Nein. Meistens liegt der Betrag nahe bei 125 Punkten, dh bei einem Durchschnittswert. Und als Ergebnis - noch bevor Sie einen Wurf machen - können Sie das zukünftige Ergebnis grob abschätzen.
Der Grund ist, dass es die größte Anzahl von Kombinationen gibt, um die durchschnittliche Anzahl von Punkten zu erhalten. Je weiter davon entfernt, desto weniger Kombinationen - und dementsprechend auch die Wahrscheinlichkeit eines Verlusts. Wenn Sie diese Daten visualisieren, ähneln sie aus der Ferne der Form einer Glocke. Daher kann mit einer gewissen Dehnung ein System von 10 Knochen als RNG mit einer Normalverteilung bezeichnet werden.
Ein weiteres Beispiel, nur schon im Flugzeug - Zielschießen. Der Schütze ist der RNG, der ein Zahlenpaar (x, y) generiert, das in der Grafik angezeigt wird.
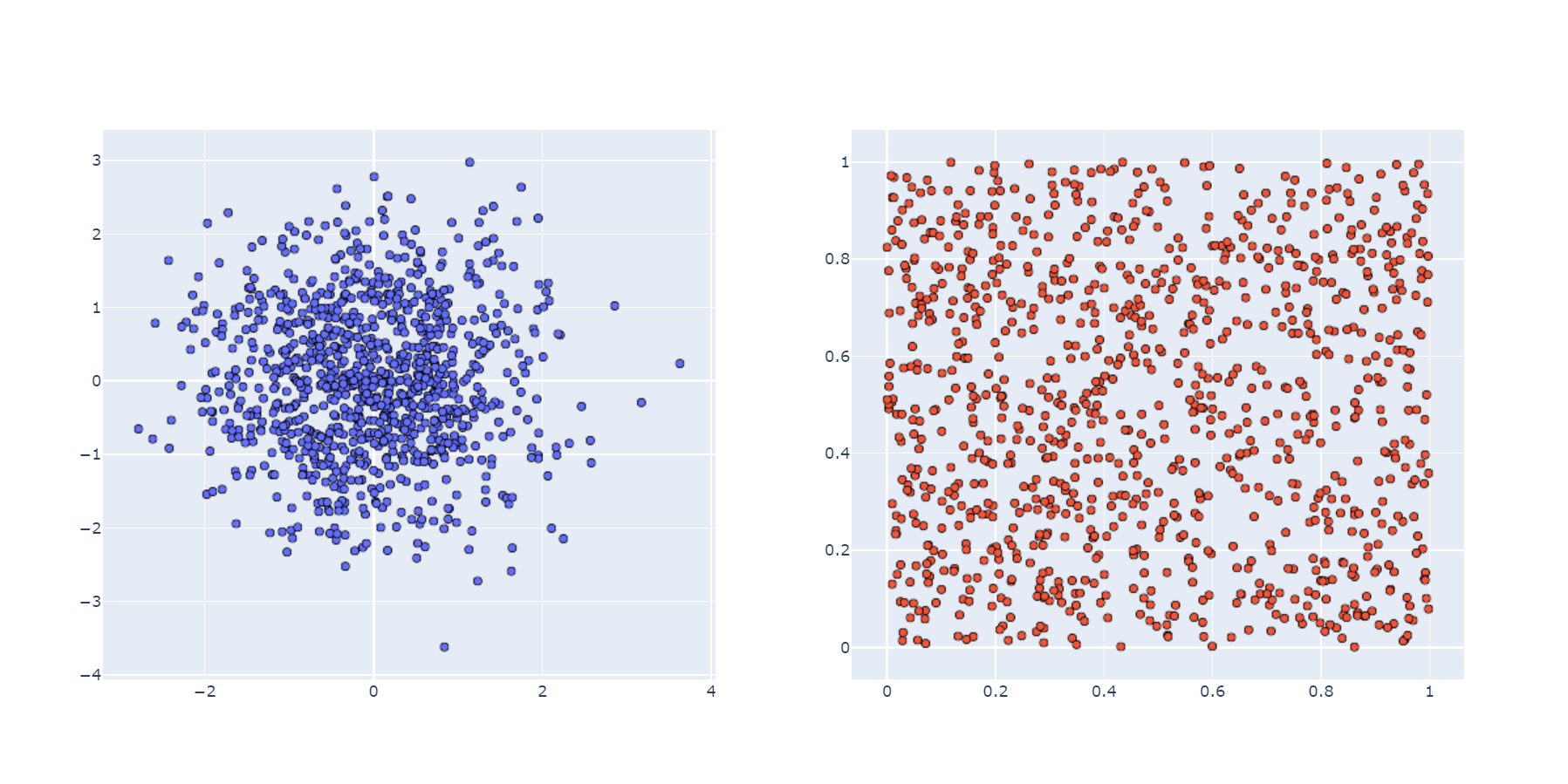
Stimmen Sie zu, dass die Option auf der linken Seite näher am wirklichen Leben liegt - dies ist ein RNG mit einer Normalverteilung. Wenn Sie jedoch Sterne an einem dunklen Himmel streuen müssen, ist die richtige Option, die mit Hilfe eines RNG mit gleichmäßiger Verteilung erzielt wird, besser. Wählen Sie im Allgemeinen je nach Aufgabe einen Generator.
Lassen Sie uns nun über die Entropie der PSP-Sequenz sprechen. Zum Beispiel gibt es eine Sequenz, die so beginnt:
89, 93, 33, 32, 82, 21, 4, 42, 11, 8, 60, 95, 53, 30, 42, 19, 34, 35, 62, 23, 44, 38, 74, 36, 52, 18, 58, 79, 65, 45, 99, 90, 82, 20, 41, 13, 88, 76, 82, 24, 5, 54, 72, 19, 80, 2, 74, 36, 71, 9, ...
Wie zufällig sind diese Zahlen auf den ersten Blick? Beginnen wir mit der Überprüfung der Verteilung.
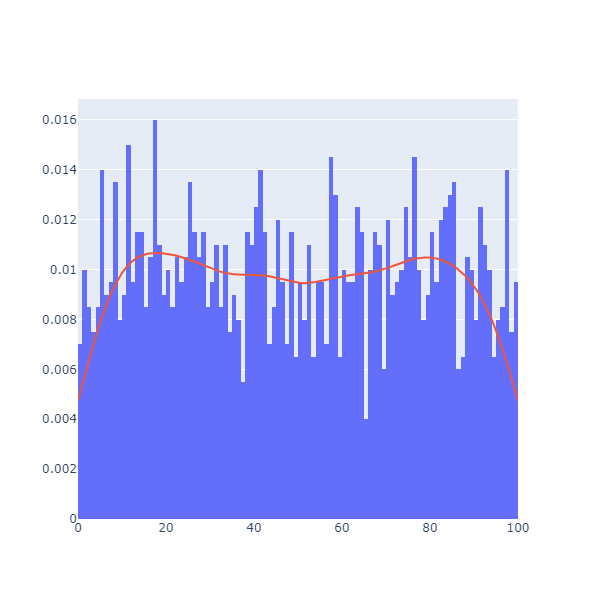
Es sieht fast wie eine Uniform aus, aber wenn Sie die Folge von zwei Zahlen lesen und sie als Koordinaten in der Ebene interpretieren, erhalten Sie Folgendes:
Muster sind deutlich sichtbar. Und da die Daten in der Sequenz auf eine bestimmte Weise geordnet sind (dh sie haben eine niedrige Entropie), kann dies zu einer sehr „Verzerrung“ führen. Zumindest ist ein solches PRNG nicht sehr geeignet, um Koordinaten in einer Ebene zu erzeugen.
Eine andere Sequenz:
42, 72, 17, 0, 30, 0, 15, 9, 47, 19, 35, 86, 40, 54, 97, 42, 69, 19, 20, 88, 4, 3, 67, 27, 42, 56, 17, 14, 20, 40, 80, 97, 1, 31, 69, 13, 88, 89, 76, 9, 4, 85, 17, 88, 70, 10, 42, 98, 96, 53, ...
Auch im Flugzeug scheint hier alles in Ordnung zu sein:
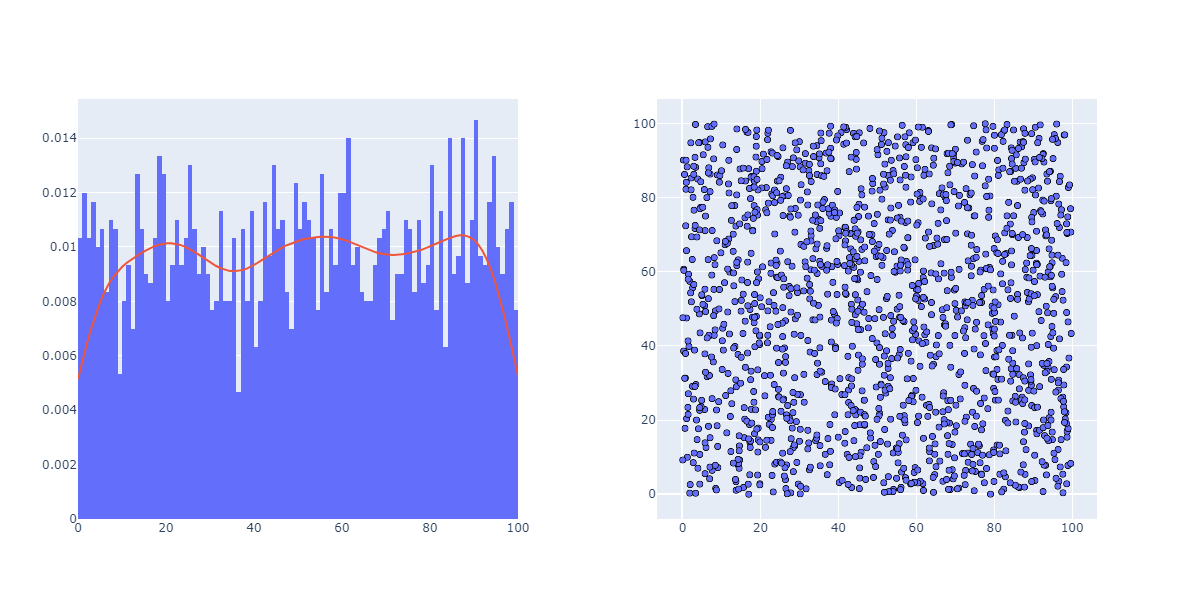
Mal sehen in Band (wir lesen jeweils drei Zahlen):
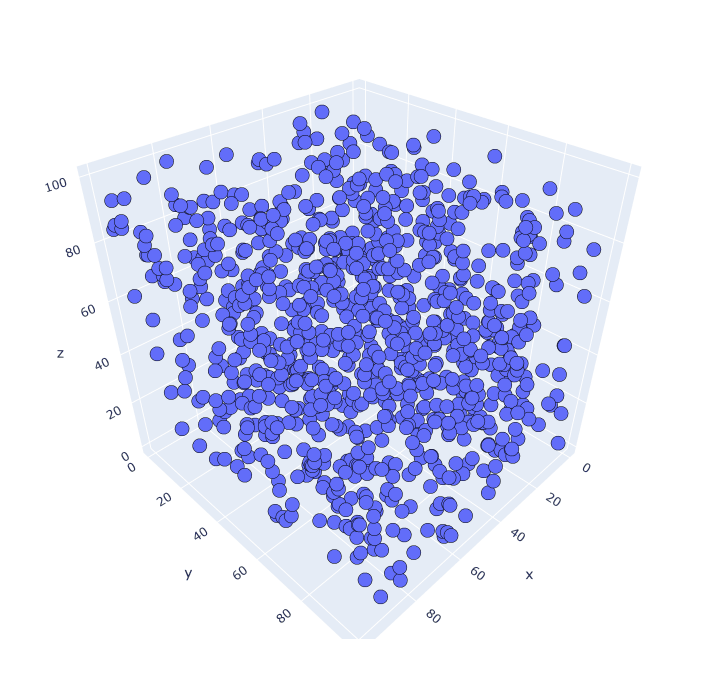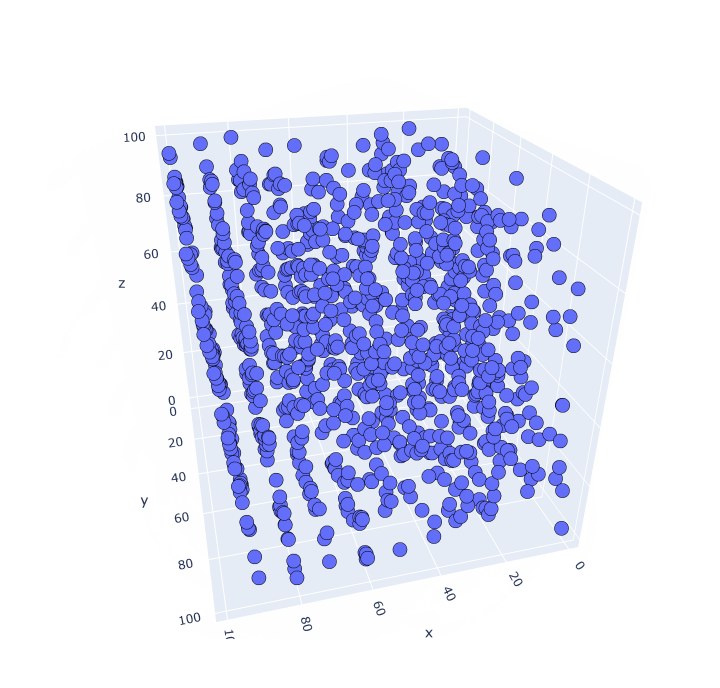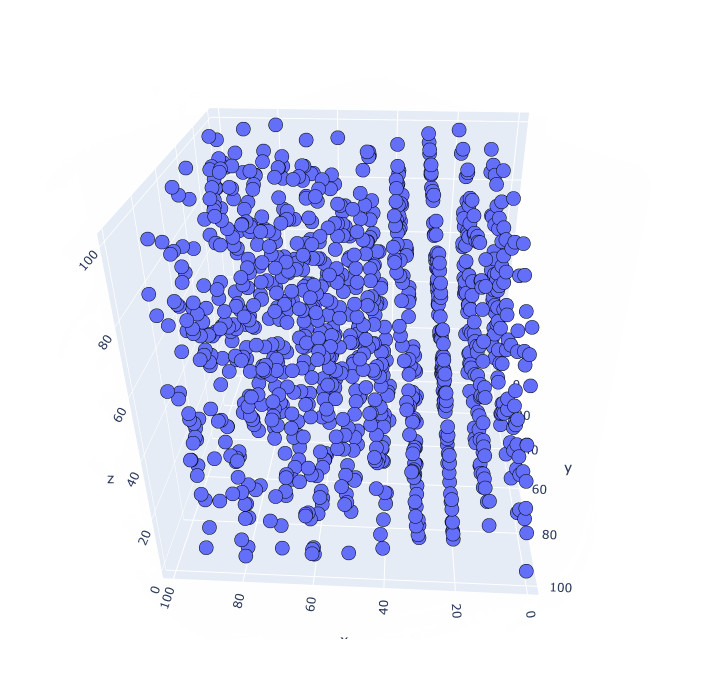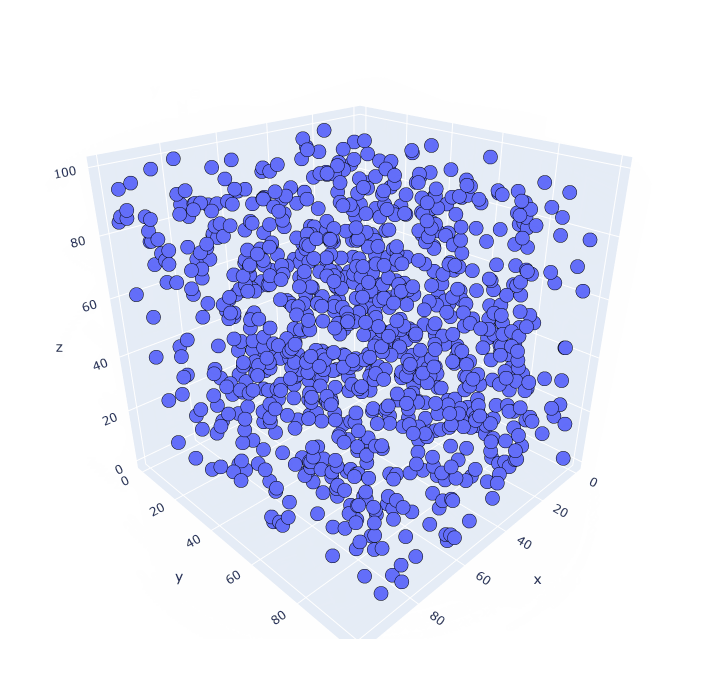
Und wieder die Muster. Build-Visualisierung in vier Dimensionen funktioniert nicht. Muster können jedoch sowohl in dieser als auch in großen Dimensionen existieren.
In derselben Kryptographie, in der die strengsten Anforderungen an das PRNG gestellt werden, ist eine solche Situation kategorisch inakzeptabel. Um ihre Qualität zu bewerten, wurden daher spezielle Algorithmen entwickelt, auf die wir jetzt nicht eingehen werden. Das Thema ist umfangreich und stützt sich auf einen separaten Artikel.
Testen
Wenn wir etwas nicht genau wissen, wie soll man dann damit arbeiten? Lohnt es sich, die Straße zu überqueren, wenn Sie nicht wissen, welche Verkehrsampel es zulässt? Die Folgen können unterschiedlich sein.
Gleiches gilt für die berüchtigte Zufälligkeit in der Einheit. Nun, wenn die Dokumentation die notwendigen Details enthüllt, aber die am Anfang des Artikels erwähnte Geschichte nur wegen des Mangels an gewünschten Einzelheiten passiert ist.
Und ohne zu wissen, wie das Tool funktioniert, können Sie es nicht richtig anwenden. Im Allgemeinen ist es an der Zeit, ein Experiment zu überprüfen und durchzuführen, um schließlich zumindest auf Kosten der Verteilung sicherzustellen.
Die Lösung war einfach und effektiv - Statistiken zu sammeln, objektive Daten zu erhalten und die Ergebnisse zu betrachten.
Forschungsgegenstand
Es gibt verschiedene Möglichkeiten, in Unity Zufallszahlen zu generieren - wir haben fünf getestet.
- System.Random.Next (). Erzeugt Ganzzahlen in einem bestimmten Wertebereich.
- System.Random.NextDouble (). Erzeugt Zahlen mit doppelter Genauigkeit (double) im Bereich von [0; 1).
- UnityEngine.Random.Range (). Erzeugt Zahlen mit einfacher Genauigkeit (float) in einem bestimmten Wertebereich.
- UnityEngine.Random.value. Erzeugt Zahlen mit einfacher Genauigkeit (float) im Bereich von [0; 1).
- Unity.Mathematics.Random.NextFloat (). Teil der neuen Unity.Mathematics-Bibliothek. Erzeugt Zahlen mit einfacher Genauigkeit (float) in einem bestimmten Wertebereich.
Fast überall in der Dokumentation wurde eine gleichmäßige Verteilung angegeben, mit Ausnahme von UnityEngine.Random.value (wo die Verteilung nicht angegeben ist, aber ähnlich wie bei UnityEngine.Random.Range () wurde auch erwartet, dass sie einheitlich ist) und Unity.Mathematics.Random.NextFloat () (wo in Grundlage ist der Xorshift-Algorithmus, dh Sie müssen erneut auf eine gleichmäßige Verteilung warten.
Standardmäßig wurden die in der Dokumentation erwarteten Werte für die erwarteten Ergebnisse verwendet.
Methodik
Wir haben eine kleine Anwendung geschrieben, die in jeder der vorgestellten Methoden Folgen von Zufallszahlen generiert und die Ergebnisse für die weitere Verarbeitung gespeichert hat.
Die Länge jeder Sequenz beträgt 100.000 Zahlen.
Der Bereich der Zufallszahlen ist [0, 100].
Daten wurden von mehreren Zielplattformen gesammelt:
- Windows
- Unity v2018.3.14f1, Editor-Modus, Mono, .NET Standard 2.0 - macOS
- Unity v2018.3.14f1, Editor-Modus, Mono, .NET Standard 2.0
- Unity v5.6.4p4, Editor-Modus, Mono, .NET Standard 2.0 - Android
- Unity v2018.3.14f1, Assembly auf dem Gerät, Mono, .NET Standard 2.0 - iOS
- Unity v2018.3.14f1, Build to Device, il2cpp, .NET Standard 2.0
Implementierung
Wir haben verschiedene Möglichkeiten, Zufallszahlen zu generieren. Für jeden von ihnen schreiben wir eine separate Wrapper-Klasse, die Folgendes bereitstellen sollte:
- Möglichkeit zum Einstellen des Wertebereichs [min / max]. Es wird über den Konstruktor festgelegt.
- Methode, die den mittleren Bereich zurückgibt. Wir werden float als allgemeineren Typ wählen.
- Der Name der Generierungsmethode zum Markieren der Ergebnisse. Der Einfachheit halber geben wir den vollständigen Klassennamen + den Namen der Methode zurück, mit der der Mitteltonbereich als Wert generiert wurde.
Deklarieren Sie zunächst eine Abstraktion, die von der IRandomGenerator-Schnittstelle dargestellt wird:
namespace RandomDistribution { public interface IRandomGenerator { string Name { get; } float Generate(); } }
Implementierung von System.Random.Next ()
Mit dieser Methode können Sie einen Wertebereich angeben, es werden jedoch Ganzzahlen zurückgegeben, und es wird ein Gleitkommawert benötigt. Sie können Integer einfach als Float interpretieren oder den Wertebereich um mehrere Größenordnungen erweitern und diese bei jeder Generierung des Mitteltöners kompensieren. Es wird sich so etwas wie ein Festpunkt mit der angegebenen Genauigkeit herausstellen. Wir werden diese Option verwenden, da sie näher am realen Float-Wert liegt.
using System; namespace RandomDistribution { public class SystemIntegerRandomGenerator : IRandomGenerator { private const int DefaultFactor = 100000; private readonly Random _generator = new Random(); private readonly int _min; private readonly int _max; private readonly int _factor; public string Name => "System.Random.Next()"; public SystemIntegerRandomGenerator(float min, float max, int factor = DefaultFactor) { _min = (int)min * factor; _max = (int)max * factor; _factor = factor; } public float Generate() => (float)_generator.Next(_min, _max) / _factor; } }
Implementierung von System.Random.NextDouble ()
Hier ein fester Wertebereich [0; 1). Um es auf das im Konstruktor angegebene zu projizieren, verwenden wir eine einfache Arithmetik: X * (max - min) + min.
using System; namespace RandomDistribution { public class SystemDoubleRandomGenerator : IRandomGenerator { private readonly Random _generator = new Random(); private readonly double _factor; private readonly float _min; public string Name => "System.Random.NextDouble()"; public SystemDoubleRandomGenerator(float min, float max) { _factor = max - min; _min = min; } public float Generate() => (float)(_generator.NextDouble() * _factor) + _min; } }
Implementierung von UnityEngine.Random.Range ()
Mit dieser Methode der statischen Klasse UnityEngine.Random können Sie einen Wertebereich angeben und einen mittleren Bereich vom Typ float zurückgeben. Es sind keine zusätzlichen Transformationen erforderlich.
using UnityEngine; namespace RandomDistribution { public class UnityRandomRangeGenerator : IRandomGenerator { private readonly float _min; private readonly float _max; public string Name => "UnityEngine.Random.Range()"; public UnityRandomRangeGenerator(float min, float max) { _min = min; _max = max; } public float Generate() => Random.Range(_min, _max); } }
Implementierung von UnityEngine.Random.value
Die value-Eigenschaft der statischen Klasse UnityEngine.Random gibt einen mittleren Bereich vom Typ float aus einem festen Wertebereich zurück [0; 1). Wir projizieren es auf die gleiche Weise wie bei der Implementierung von System.Random.NextDouble () auf einen bestimmten Bereich.
using UnityEngine; namespace RandomDistribution { public class UnityRandomValueGenerator : IRandomGenerator { private readonly float _factor; private readonly float _min; public string Name => "UnityEngine.Random.value"; public UnityRandomValueGenerator(float min, float max) { _factor = max - min; _min = min; } public float Generate() => (float)(Random.value * _factor) + _min; } }
Implementierung von Unity.Mathematics.Random.NextFloat ()
Die NextFloat () -Methode der Unity.Mathematics.Random-Klasse gibt einen mittleren Bereich vom Typ float zurück und ermöglicht die Angabe eines Wertebereichs. Die einzige Nuance ist, dass jede Instanz von Unity.Mathematics.Random mit einem Startwert initialisiert werden muss - auf diese Weise vermeiden wir, dass wiederholte Sequenzen generiert werden.
using Unity.Mathematics; namespace RandomDistribution { public class UnityMathematicsRandomValueGenerator : IRandomGenerator { private Random _generator; private readonly float _min; private readonly float _max; public string Name => "Unity.Mathematics.Random.NextFloat()"; public UnityMathematicsRandomValueGenerator(float min, float max) { _min = min; _max = max; _generator = new Random(); _generator.InitState(unchecked((uint)System.DateTime.Now.Ticks)); } public float Generate() => _generator.NextFloat(_min, _max); } }
MainController-Implementierung
Mehrere IRandomGenerator-Implementierungen sind bereit. Als Nächstes müssen Sie Sequenzen generieren und den resultierenden Datensatz zur Verarbeitung speichern. Erstellen Sie dazu eine Szene in Unity und ein kleines Skript MainController, das alle erforderlichen Arbeiten ausführt und gleichzeitig für die Interaktion mit der Benutzeroberfläche verantwortlich ist.
Wir legen die Größe des Datasets und den Bereich der Mittelbereichswerte fest und erhalten eine Methode, die ein Array von optimierten und gebrauchsfertigen Generatoren zurückgibt.
namespace RandomDistribution { public class MainController : MonoBehaviour { private const int DefaultDatasetSize = 100000; public float MinValue = 0f; public float MaxValue = 100f; ... private IRandomGenerator[] CreateRandomGenerators() { return new IRandomGenerator[] { new SystemIntegerRandomGenerator(MinValue, MaxValue), new SystemDoubleRandomGenerator(MinValue, MaxValue), new UnityRandomRangeGenerator(MinValue, MaxValue), new UnityRandomValueGenerator(MinValue, MaxValue), new UnityMathematicsRandomValueGenerator(MinValue, MaxValue) }; } ... } }
Und jetzt bilden wir einen Datensatz. In diesem Fall wird die Datengenerierung mit der Aufzeichnung der Ergebnisse in einem Textstrom (im CSV-Format) kombiniert. Um die Werte jedes IRandomGenerators zu speichern, wird eine separate Spalte zugewiesen, und die erste Zeile enthält den Namen des Generators.
namespace RandomDistribution { public class MainController : MonoBehaviour { ... private void GenerateCsvDataSet(TextWriter writer, int dataSetSize, params IRandomGenerator[] generators) { const char separator = ','; int lastIdx = generators.Length - 1;
Es bleibt, die GenerateCsvDataSet-Methode aufzurufen und das Ergebnis in einer Datei zu speichern oder Daten sofort über das Netzwerk vom Endgerät zum empfangenden Server zu übertragen.
namespace RandomDistribution { public class MainController : MonoBehaviour { ... public void GenerateCsvDataSet(string path, int dataSetSize, params IRandomGenerator[] generators) { using (var writer = File.CreateText(path)) { GenerateCsvDataSet(writer, dataSetSize, generators); } } public string GenerateCsvDataSet(int dataSetSize, params IRandomGenerator[] generators) { using (StringWriter writer = new StringWriter(CultureInfo.InvariantCulture)) { GenerateCsvDataSet(writer, dataSetSize, generators); return writer.ToString(); } } ... } }
Die Projektquellen befinden sich auf
GitLab .
Ergebnisse
Es geschah kein Wunder. Was sie erwartet hatten, bekamen sie - in allen Fällen eine gleichmäßige Verteilung ohne einen Hinweis auf Verschwörungen. Ich sehe keinen Sinn darin, separate Grafiken auf den Plattformen anzuwenden - alle zeigen ungefähr die gleichen Ergebnisse.
Die Realität ist:
Visualisierung von Sequenzen in einer Ebene aus allen fünf Generierungsmethoden:
Und Visualisierung in 3D. Ich werde nur das Ergebnis von System.Random.Next () belassen, um nicht den gleichen Inhalt zu erzeugen.
Die in der Einleitung erzählte Geschichte über die Normalverteilung von UnityEngine.Random wiederholte sich nicht: Entweder war sie anfangs fehlerhaft oder seitdem hat sich etwas an der Engine geändert. Aber jetzt sind wir sicher.