Einführung in funktionale Abhängigkeiten

In diesem Artikel werden wir über funktionale Abhängigkeiten in Datenbanken sprechen - was es ist, wo es angewendet wird und welche Algorithmen für ihre Suche existieren.

Wir werden funktionale Abhängigkeiten im Kontext relationaler Datenbanken betrachten. In solchen Datenbanken werden Informationen in Form von Tabellen gespeichert. Außerdem verwenden wir ungefähre Konzepte, die in einer strengen relationalen Theorie nicht austauschbar sind: Wir nennen die Tabelle selbst eine Beziehung, Spalten - Attribute (ihre Menge ist ein Beziehungsdiagramm) und eine Menge von Zeilenwerten für eine Teilmenge von Attributen - ein Tupel.



In der obigen Tabelle ist (Benson, M, M Organ ) beispielsweise ein Tupel von Attributen (Patient, Geschlecht, Arzt) .
Formal wird dies wie folgt geschrieben: $$$t_ {1}$ [ Patient, Paul, Doktor ] = (Benson, M, M Organ) .
Jetzt können wir das Konzept der funktionalen Abhängigkeit (FZ) einführen:

Definition 1. Die Beziehung R erfüllt das Bundesgesetz X → Y (wobei X, Y ⊆ R) genau dann, wenn für Tupel $$$t_ {1}$ , $$$t_ {2}$ ∈ R gilt: wenn $$$t_ {1}$ [X] = $$$t_ {2}$ [X] dann $$$t_ {1}$ [Y] = $$$t_ {2}$ [Y]. In diesem Fall wird gesagt, dass X (eine Determinante oder eine definierende Menge von Attributen) Y (eine abhängige Menge) funktional definiert.

Mit anderen Worten bedeutet das Vorhandensein des Bundesgesetzes X → Y , dass wenn wir zwei Tupel in R haben und sie in den Attributen von X übereinstimmen, sie auch in den Attributen von Y übereinstimmen.
Und jetzt in Ordnung. Betrachten Sie die Attribute Patient und Geschlecht , für die wir herausfinden möchten, ob zwischen ihnen Abhängigkeiten bestehen oder nicht. Für so viele Attribute können die folgenden Abhängigkeiten bestehen:

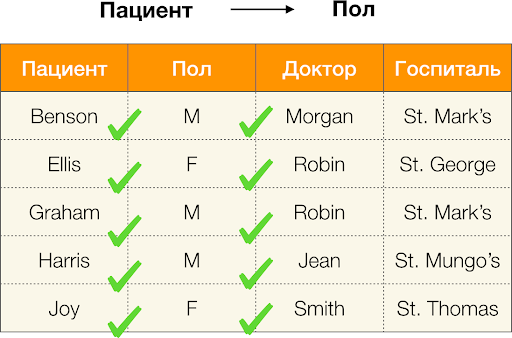
1. Patient → Geschlecht
2. Geschlecht → Patient

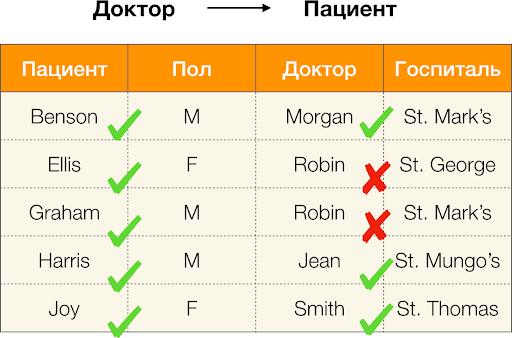
Gemäß der obigen Definition muss nur ein Wert der Spalte Geschlecht jedem eindeutigen Wert der Spalte Patient entsprechen, um die erste Abhängigkeit aufrechtzuerhalten. Und für die Beispieltabelle gilt dies. Dies funktioniert jedoch nicht in die entgegengesetzte Richtung, dh die zweite Abhängigkeit ist nicht erfüllt, und das Paul- Attribut ist keine Determinante für den Patienten . Wenn Sie die Abhängigkeit Arzt → Patient nehmen , können Sie ebenfalls feststellen, dass sie verletzt ist, da der Robin- Wert für dieses Attribut mehrere unterschiedliche Werte hat - Ellis und Graham .

Funktionale Abhängigkeiten ermöglichen es somit, die vorhandenen Beziehungen zwischen den Mengen von Tabellenattributen zu bestimmen. Von nun an werden wir die interessantesten Beziehungen oder vielmehr X → Y so betrachten, dass sie sind:

• nicht trivial, dh die rechte Seite der Abhängigkeit ist keine Teilmenge der linken (Y ̸⊆ X) ;
• minimal, das heißt, es gibt keine solche Abhängigkeit Z → Y, so dass Z ⊂ X ist.

Die bis zu diesem Zeitpunkt berücksichtigten Abhängigkeiten waren streng, dh sie enthielten keine Verstöße in der Tabelle, aber neben ihnen gibt es auch solche, die eine gewisse Inkonsistenz zwischen den Werten von Tupeln zulassen. Solche Abhängigkeiten werden in eine separate Klasse eingeordnet, die als ungefähr bezeichnet wird, und dürfen bei einer bestimmten Anzahl von Tupeln verletzt werden. Dieser Betrag wird durch die maximale Emax-Fehleranzeige geregelt. Zum Beispiel der Fehleranteil $$$e_ {max}$ = 0,01 kann bedeuten, dass die Abhängigkeit von 1% der verfügbaren Tupel von der betrachteten Menge von Attributen verletzt werden kann. Das heißt, für 1000 Datensätze können maximal 10 Tupel gegen das Bundesgesetz verstoßen. Wir werden eine etwas andere Metrik betrachten, die auf paarweise unterschiedlichen Werten der verglichenen Tupel basiert. Für die Abhängigkeit X → Y von der Beziehung r wird wie folgt angenommen:

$$

$$e (X \ rechter Pfeil Y, r) = \ frac {| \ {(t_1, t_2) \ in r ^ 2 \ | \ t_1 [X] = t_2 [X] \ Keil t_1 [Y] \ neq t_2 [Y] \} |} {| r ^ 2 | - | r |}$$

Wir berechnen den Fehler für Arzt → Patient aus dem obigen Beispiel. Wir haben zwei Tupel, deren Werte sich beim Patientenattribut unterscheiden, beim Arzt jedoch übereinstimmen: $$$t_ {1}$ [ Doktor, Patient ] = ( Robin, Ellis ) und $$$t_ {2}$ [ Doktor, Patient ] = ( Robin, Graham ). Nach der Definition des Fehlers müssen wir alle widersprüchlichen Paare berücksichtigen, was bedeutet, dass es zwei davon geben wird: $$$t_ {1}$ , $$$t_ {2}$ ) und seine Umkehrung ( $$$t_ {2}$ , $$$t_ {1}$ ) Ersetzen Sie in der Formel und erhalten Sie:

$$

$$\ frac {2} {5 ^ 2 - 5} = 0,1$$

Versuchen wir nun, die Frage zu beantworten: „Warum ist das alles?“. In der Tat sind Bundesgesetze unterschiedlich. Der erste Typ sind Abhängigkeiten, die vom Administrator in der Phase des Datenbankentwurfs festgelegt werden. Normalerweise sind es nur wenige, sie sind streng und die Hauptanwendung ist die Datennormalisierung und das Design des Beziehungsschemas.

Der zweite Typ sind Abhängigkeiten, die "versteckte" Daten und zuvor unbekannte Beziehungen zwischen Attributen darstellen. Das heißt, solche Abhängigkeiten wurden zum Zeitpunkt des Entwurfs nicht berücksichtigt und sind bereits für den vorhandenen Datensatz vorhanden, sodass auf der Grundlage der identifizierten Bundesgesetze Rückschlüsse auf die gespeicherten Informationen gezogen werden können. Mit solchen Abhängigkeiten arbeiten wir. Sie beschäftigen sich mit einem ganzen Bereich von Bergbaudaten mit verschiedenen Suchtechniken und Algorithmen, die auf ihrer Basis basieren. Lassen Sie uns verstehen, wie die gefundenen funktionalen Abhängigkeiten (genau oder ungefähr) in Daten nützlich sein können.



Heute gehört die Datenbereinigung zu den Hauptbereichen der Abhängigkeitsverwendung. Es beinhaltet die Entwicklung von Prozessen zur Identifizierung "schmutziger Daten" mit deren anschließender Korrektur. Helle Vertreter von "schmutzigen Daten" sind Duplikate, Datenfehler oder Tippfehler, fehlende Werte, veraltete Daten, zusätzliche Leerzeichen und dergleichen.

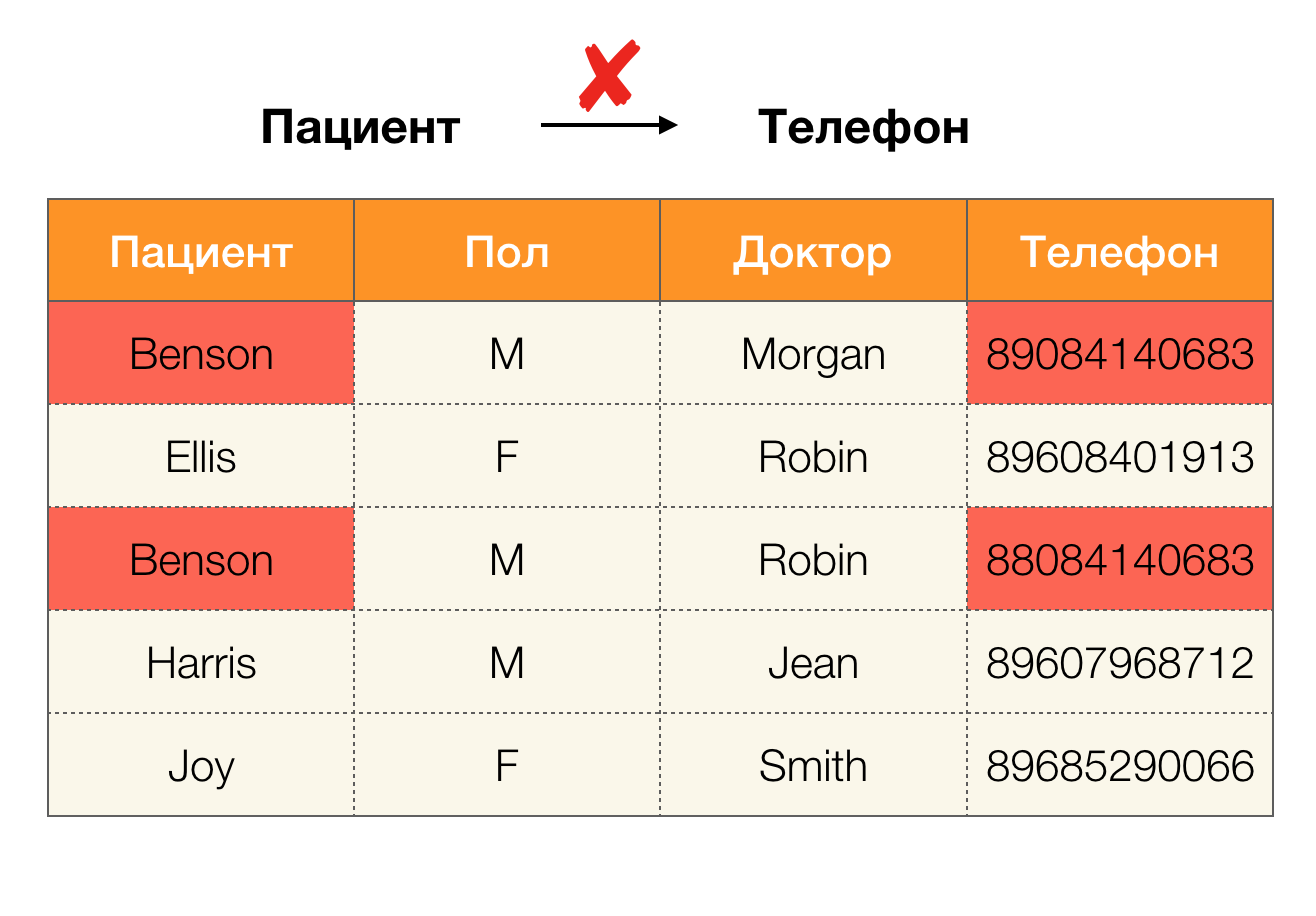
Beispiel Datenfehler:



Beispielduplikate in Daten:



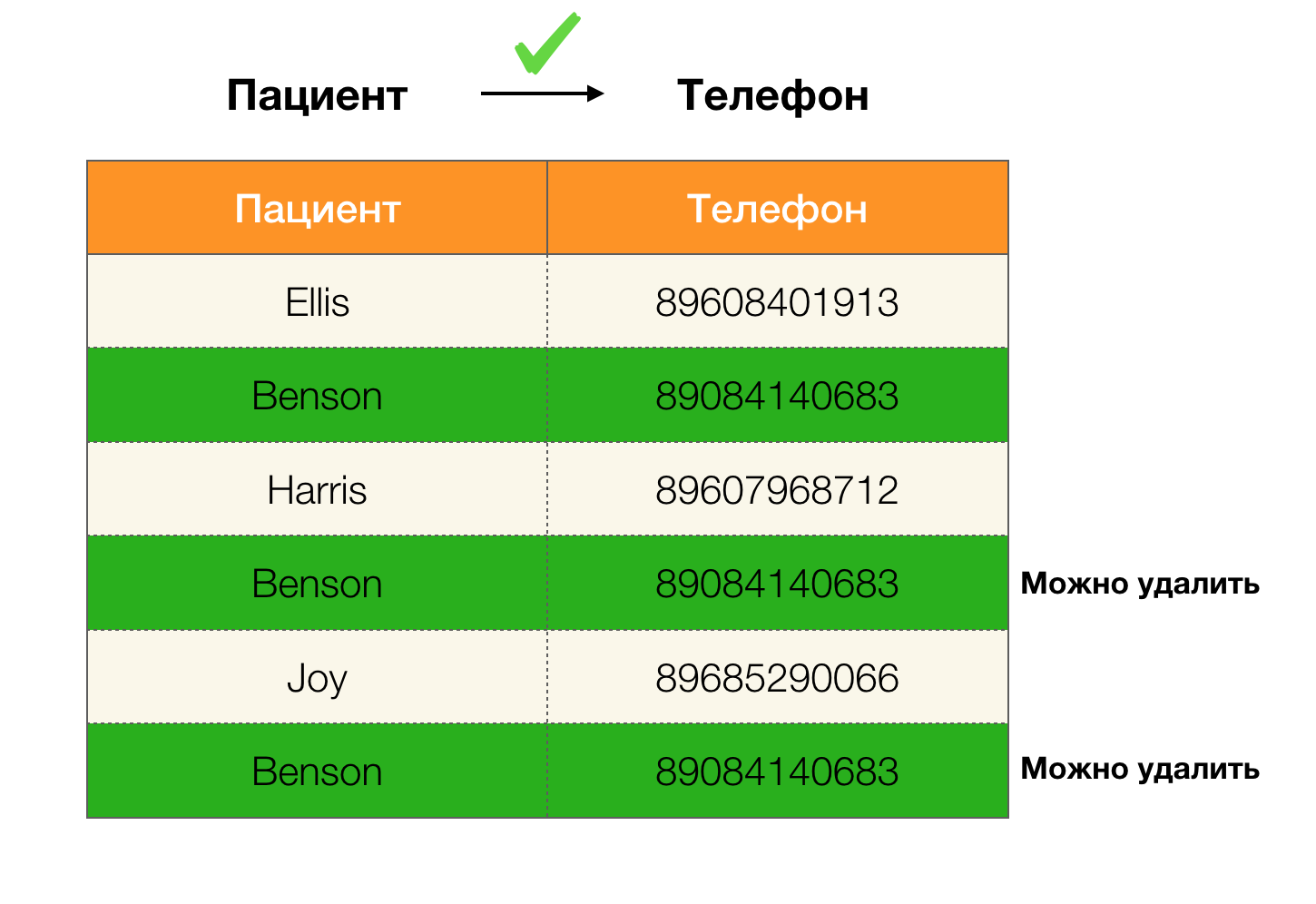
Zum Beispiel haben wir eine Tabelle und eine Reihe von Bundesgesetzen, die ausgeführt werden müssen. Bei der Datenbereinigung werden in diesem Fall die Daten so geändert, dass die Bundesgesetze korrekt sind. Gleichzeitig sollte die Anzahl der Änderungen minimal sein (für dieses Verfahren gibt es Algorithmen, auf die wir uns in diesem Artikel nicht konzentrieren werden). Das Folgende ist ein Beispiel für eine solche Datenkonvertierung. Links ist die anfängliche Beziehung, in der offensichtlich die notwendigen Bundesgesetze nicht erfüllt sind (ein Beispiel für einen Verstoß gegen eines der Bundesgesetze ist rot hervorgehoben). Auf der rechten Seite befindet sich eine aktualisierte Beziehung, in der grüne Zellen geänderte Werte anzeigen. Nach einem solchen Verfahren begannen die notwendigen Abhängigkeiten zu bestehen.



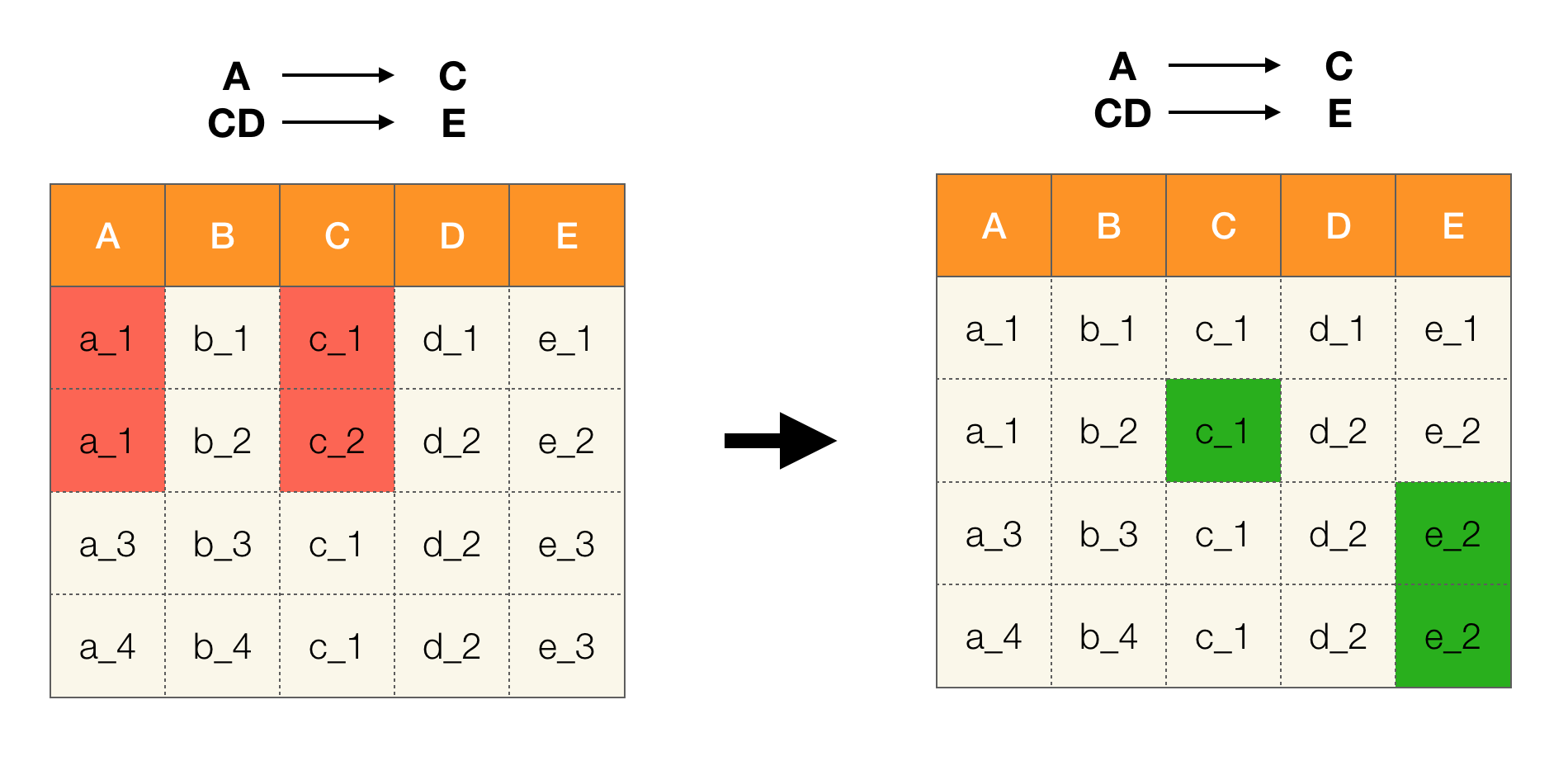
Eine weitere beliebte Anwendung ist das Datenbankdesign. Hier lohnt es sich, an Normalformen und Normalisierung zu erinnern. Normalisierung ist der Prozess, bei dem eine Beziehung mit bestimmten Anforderungen in Einklang gebracht wird, von denen jede auf ihre eigene Weise durch eine normale Form bestimmt wird. Wir werden die Anforderungen verschiedener normaler Formen nicht aufschreiben (dies wird in jedem Buch über den DB-Kurs für Anfänger gemacht), aber wir stellen nur fest, dass jede von ihnen auf ihre eigene Weise das Konzept der funktionalen Abhängigkeiten verwendet. In der Tat sind Bundesgesetze von Natur aus Integritätsbeschränkungen, die beim Entwerfen einer Datenbank berücksichtigt werden (im Rahmen dieser Aufgabe werden Bundesgesetze manchmal als Superkeys bezeichnet).

Betrachten Sie ihre Anwendung für die vier Normalformen im Bild unten. Denken Sie daran, dass die normale Boyce-Codd-Form strenger als die dritte Form ist, aber weniger streng als die vierte. Letzteres betrachten wir noch nicht, da seine Formulierung ein Verständnis mehrwertiger Abhängigkeiten erfordert, die für uns in diesem Artikel nicht von Interesse sind.






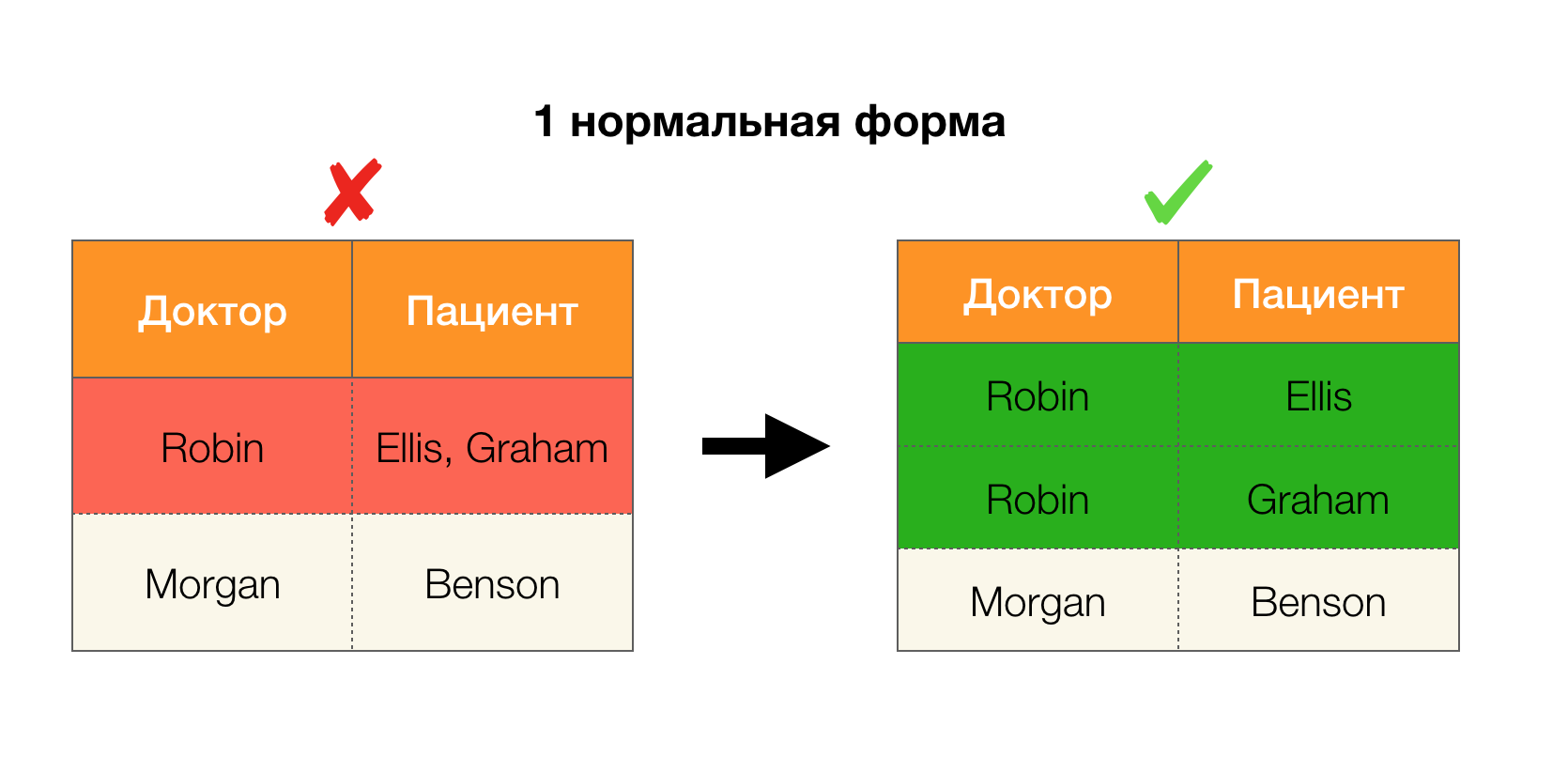
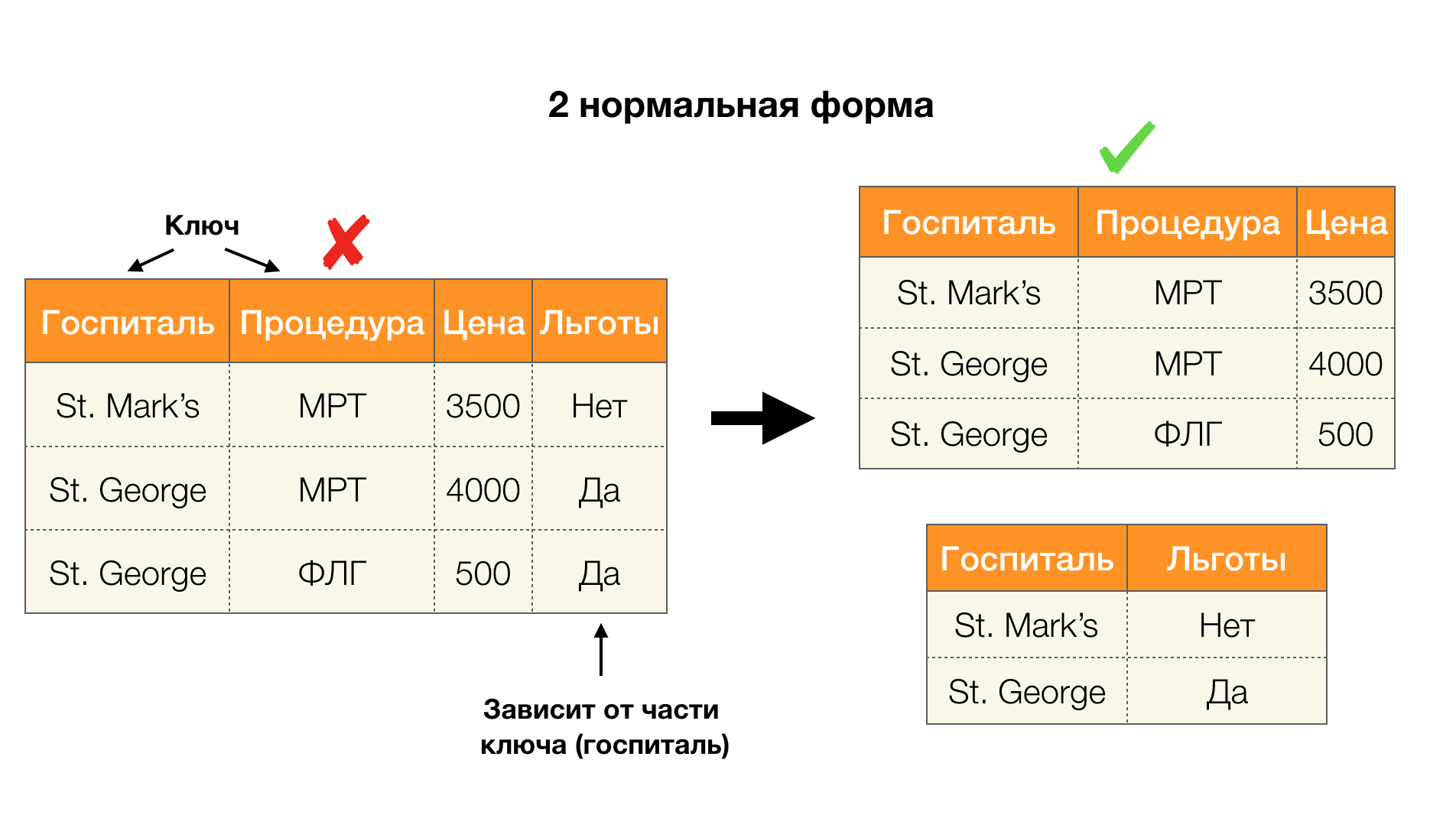
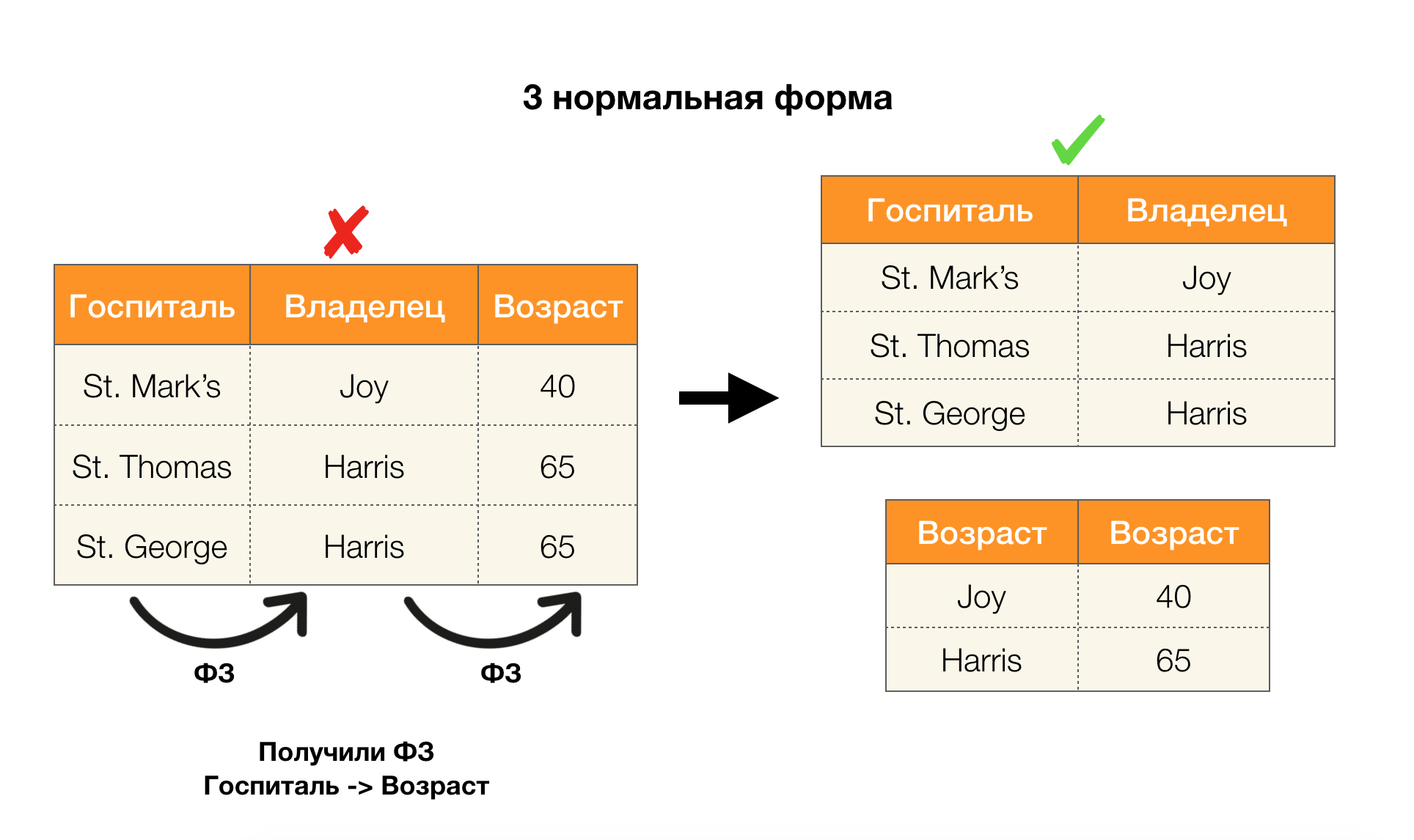
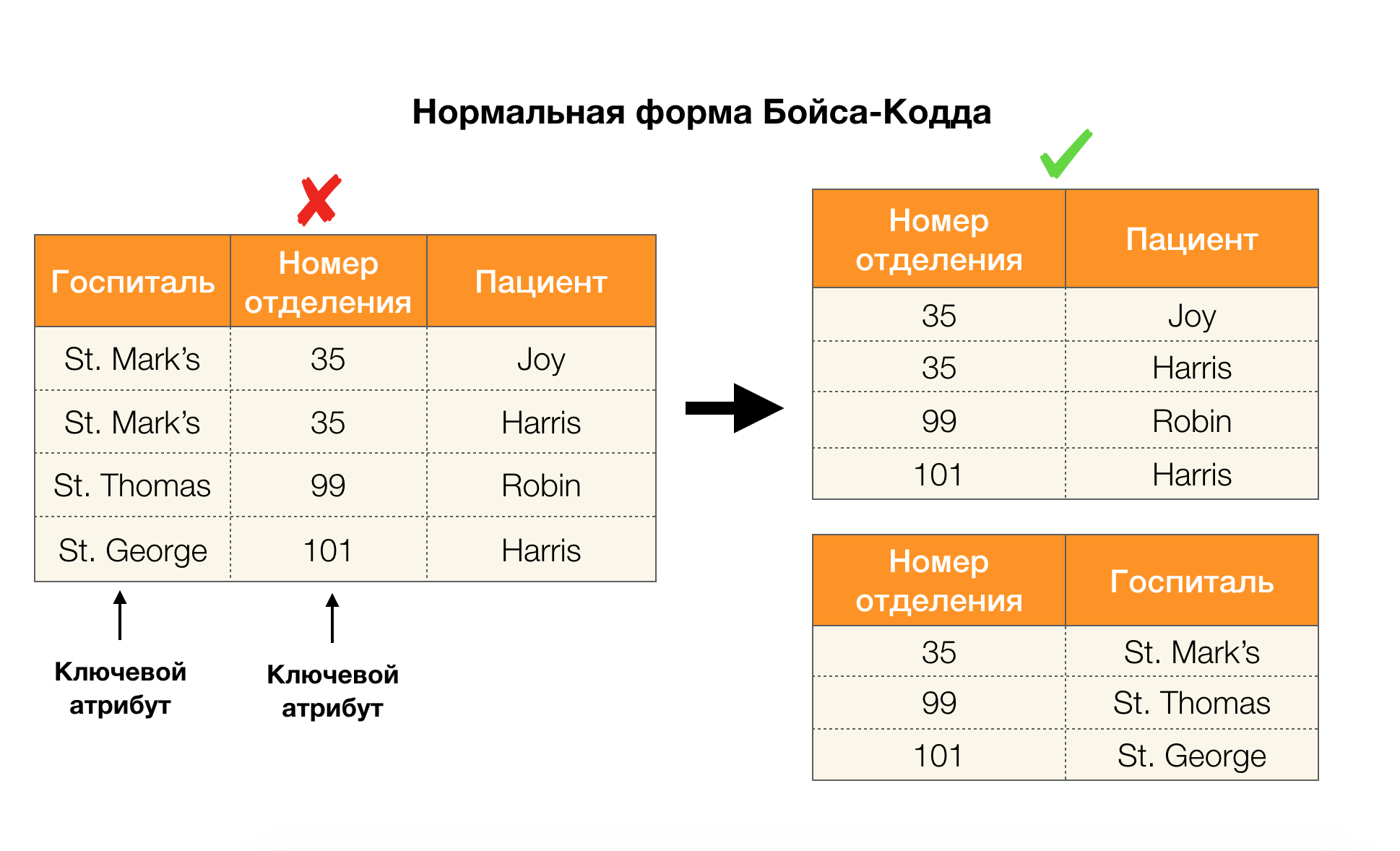
Ein weiterer Bereich, in dem Abhängigkeiten ihre Anwendung gefunden haben, ist die Reduzierung der Dimension des Merkmalsraums bei Aufgaben wie der Konstruktion eines naiven Bayes'schen Klassifikators, der Identifizierung signifikanter Merkmale und der Neuparametrisierung des Regressionsmodells. In den Originalartikeln wird dieses Problem als Definition redundanter Merkmale (Merkmalsredundanz) und relevanter Merkmale (Merkmalsrelevanz) bezeichnet [5, 6] und durch die aktive Verwendung von Datenbankkonzepten gelöst. Mit dem Aufkommen solcher Arbeiten können wir sagen, dass heute nach Lösungen gefragt ist, die es ermöglichen, die Datenbank, Analyse und Implementierung der oben genannten Optimierungsprobleme in einem Tool zu kombinieren [7, 8, 9].

Es gibt viele Algorithmen (sowohl moderne als auch nicht sehr), um in einem Datensatz nach dem Bundesgesetz zu suchen. Solche Algorithmen können in drei Gruppen unterteilt werden:

• Algorithmen unter Verwendung der Durchquerung algebraischer Gitter (Gitterdurchquerungsalgorithmen)
• Algorithmen basierend auf der Suche nach konsistenten Werten (Differenz- und Übereinstimmungsalgorithmen)
• Paarweise Vergleichsalgorithmen (Abhängigkeitsinduktionsalgorithmen)
  

Eine kurze Beschreibung der einzelnen Algorithmusarten finden Sie in der folgenden Tabelle:


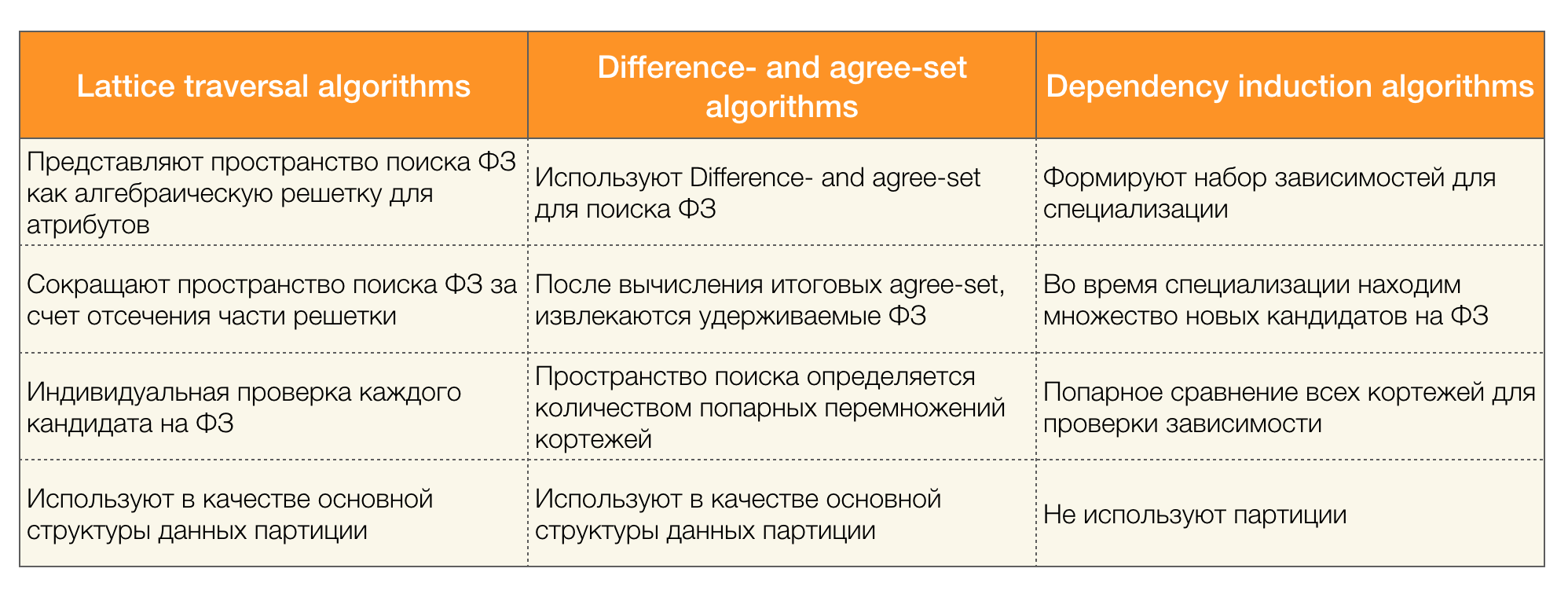
Weitere Details zu dieser Klassifizierung können gelesen werden [4]. Nachfolgend finden Sie Beispiele für Algorithmen für jeden Typ:





Derzeit erscheinen neue Algorithmen, die mehrere Ansätze zur gleichzeitigen Suche nach funktionalen Abhängigkeiten kombinieren. Beispiele für solche Algorithmen sind Pyro [2] und HyFD [3]. Eine Analyse ihrer Arbeit wird in den folgenden Artikeln dieser Reihe erwartet. In diesem Artikel werden nur die grundlegenden Konzepte und das Lemma analysiert, die zum Verständnis der Techniken zum Erkennen von Abhängigkeiten erforderlich sind.

Beginnen wir mit einem einfachen Satz - Differenz- und Übereinstimmungssatz, der in der zweiten Art von Algorithmen verwendet wird. Die Differenzmenge ist eine Menge von Tupeln, deren Werte nicht übereinstimmen, und die Übereinstimmungsmenge ist im Gegenteil eine Tupel, deren Wert übereinstimmt. Es ist zu beachten, dass wir in diesem Fall nur die linke Seite der Abhängigkeit betrachten.

Ein wichtiges Konzept, das oben erfüllt wurde, ist auch das algebraische Gitter. Da viele moderne Algorithmen mit diesem Konzept arbeiten, müssen wir eine Vorstellung davon haben, was es ist.

Um das Konzept eines Gitters einzuführen, muss eine teilweise geordnete Menge (oder eine teilweise geordnete Menge für Short-Poset) definiert werden.

Definition 2. Es wird gesagt, dass die Menge S teilweise durch die binäre Beziehung ⩽ geordnet ist, wenn für a, b, c ∈ S die folgenden Eigenschaften erfüllt sind:

1. Reflexivität, d.h.
2. Antisymmetrie, dh wenn a ⩽ b und b ⩽ a, dann ist a = b
3. Transitivität, dh für a ⩽ b und b ⩽ c folgt a ⩽ c
   

Eine solche Beziehung wird als Beziehung der (nicht strengen) Teilordnung bezeichnet, und die Menge selbst wird als teilweise geordnete Menge bezeichnet. Formale Notation: ⟨S, ⩽⟩.

Als einfachstes Beispiel einer teilweise geordneten Menge können wir die Menge aller natürlichen Zahlen N mit der üblichen Ordnungsbeziehung ⩽ nehmen. Es ist leicht zu überprüfen, ob alle notwendigen Axiome erfüllt sind.

Sinnvolleres Beispiel. Betrachten Sie die Menge aller Teilmengen {1, 2, 3}, geordnet nach der Einschlussrelation ⊆. In der Tat erfüllt diese Beziehung alle Bedingungen der Teilordnung, daher ist ⟨P ({1, 2, 3}), ⊆⟩ eine teilweise geordnete Menge. Die folgende Abbildung zeigt die Struktur dieses Satzes: Wenn Sie von einem Element entlang der Pfeile zu einem anderen Element gehen können, stehen sie in Beziehung zur Reihenfolge.



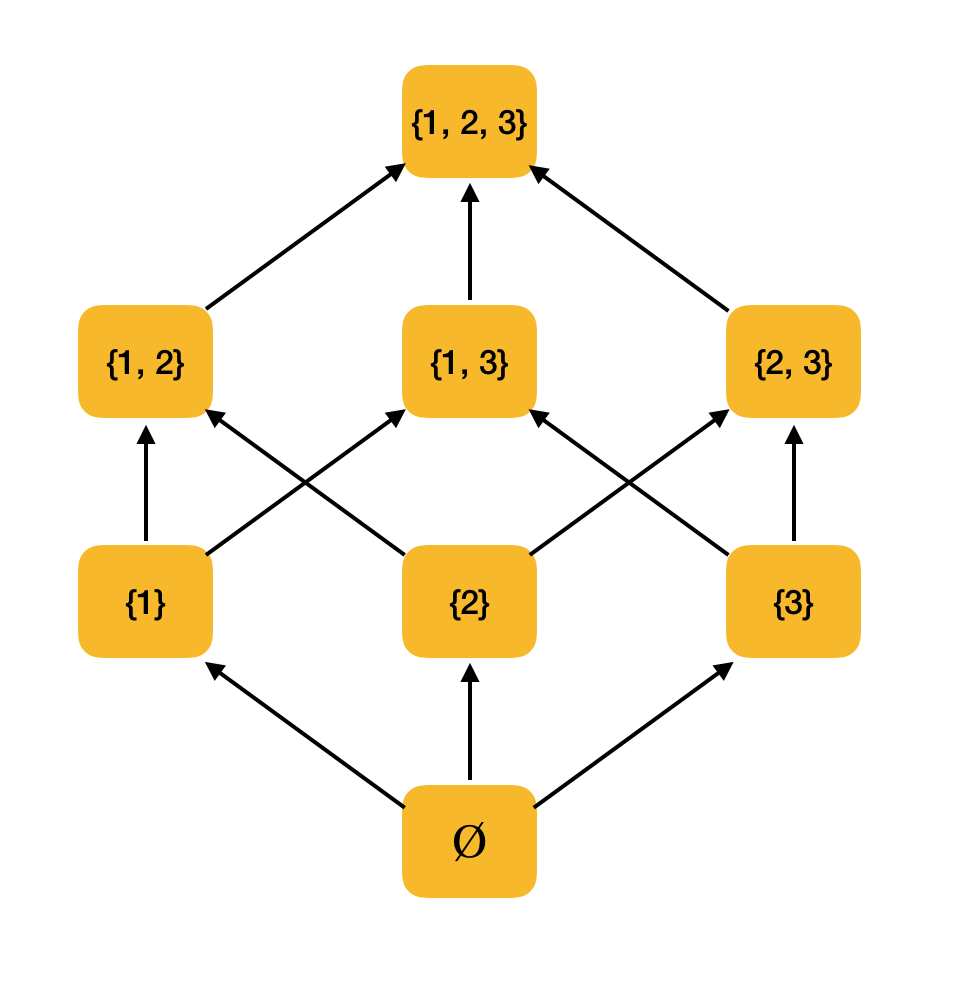
Wir brauchen zwei weitere einfache Definitionen aus dem Bereich der Mathematik - Supremum und Infimum.

Definition 3. Sei ⟨S, ⩽⟩ eine teilweise geordnete Menge, A ⊆ S. Die obere Grenze von A ist ein Element u ∈ S, so dass ∀x ∈ A: x ⩽ u. Sei U die Menge aller Obergrenzen von A. Wenn U das kleinste Element hat, dann heißt es Supremum und wird mit sup A bezeichnet.

In ähnlicher Weise wird das Konzept einer exakten Untergrenze eingeführt.

Definition 4. Sei ⟨S, ⩽⟩ eine teilweise geordnete Menge, A ⊆ S. Die untere Grenze von A ist ein Element l ∈ S, so dass ∀x ∈ A: l ⩽ x ist. Sei L die Menge aller unteren Grenzen von A. Wenn L das größte Element hat, dann heißt es ein Infimum und wird mit inf A bezeichnet.

Betrachten Sie als Beispiel die obige teilweise geordnete Menge ⟨P ({1, 2, 3}), und finden Sie das Supremum und Infimum darin:



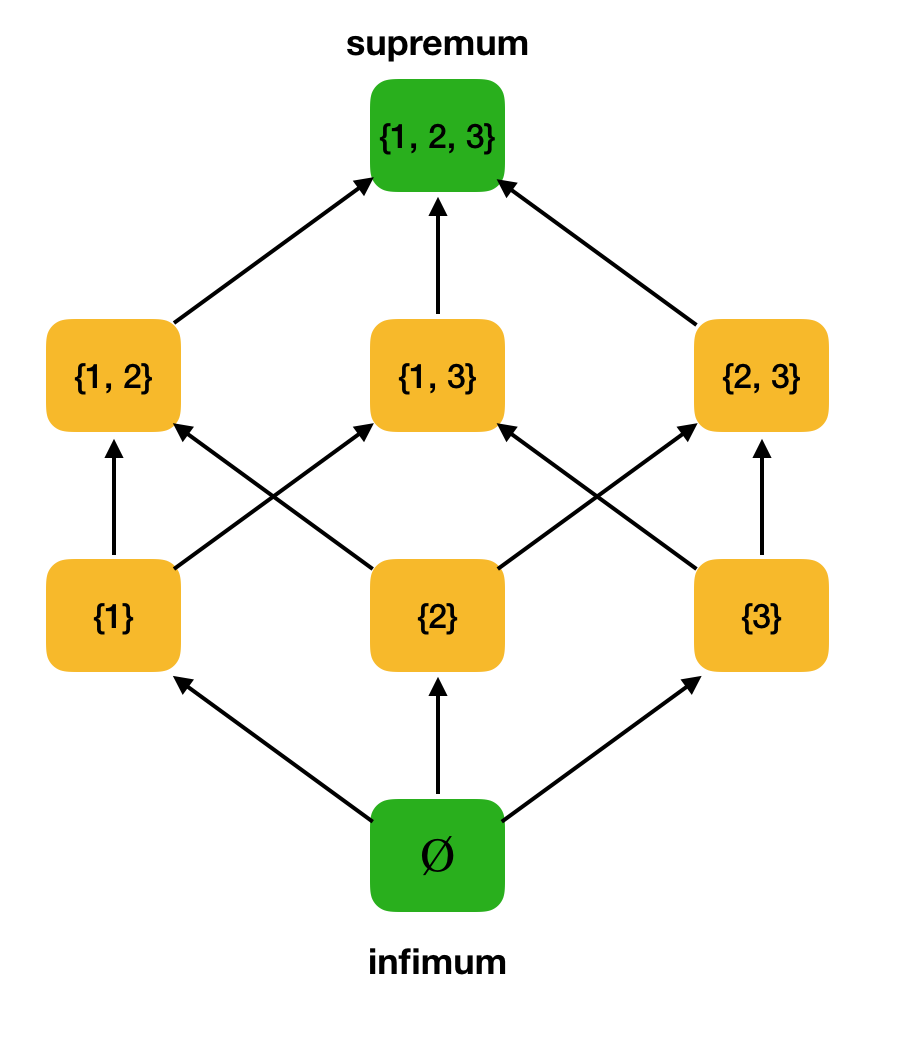
Jetzt können wir die Definition eines algebraischen Gitters formulieren.

Definition 5. Sei ⟨P, ⩽⟩ eine teilweise geordnete Menge, so dass jede Teilmenge mit zwei Elementen exakte Ober- und Untergrenzen hat. Dann heißt P ein algebraisches Gitter. Darüber hinaus wird sup {x, y} als x ∨ y und inf {x, y} - als x ∧ y geschrieben.

Wir überprüfen, ob unser Arbeitsbeispiel ⟨P ({1, 2, 3}), ⊆⟩ ein Gitter ist. In der Tat ist für jedes a, b ∈ P ({1, 2, 3}) a∨b = a∪b und a∧b = a∩b. Betrachten Sie zum Beispiel die Mengen {1, 2} und {1, 3} und finden Sie ihr Infimum und Supremum. Wenn wir sie kreuzen, erhalten wir die Menge {1}, die das Infimum sein wird. Wir bekommen das Supremum durch ihre Vereinigung - {1, 2, 3}.

In FD-Erkennungsalgorithmen wird der Suchraum häufig in Form eines Gitters dargestellt, wobei Mengen eines Elements (lesen Sie die erste Ebene des Suchgitters, wobei der linke Teil der Abhängigkeiten aus einem Attribut besteht) jedes Attribut der ursprünglichen Beziehung sind.
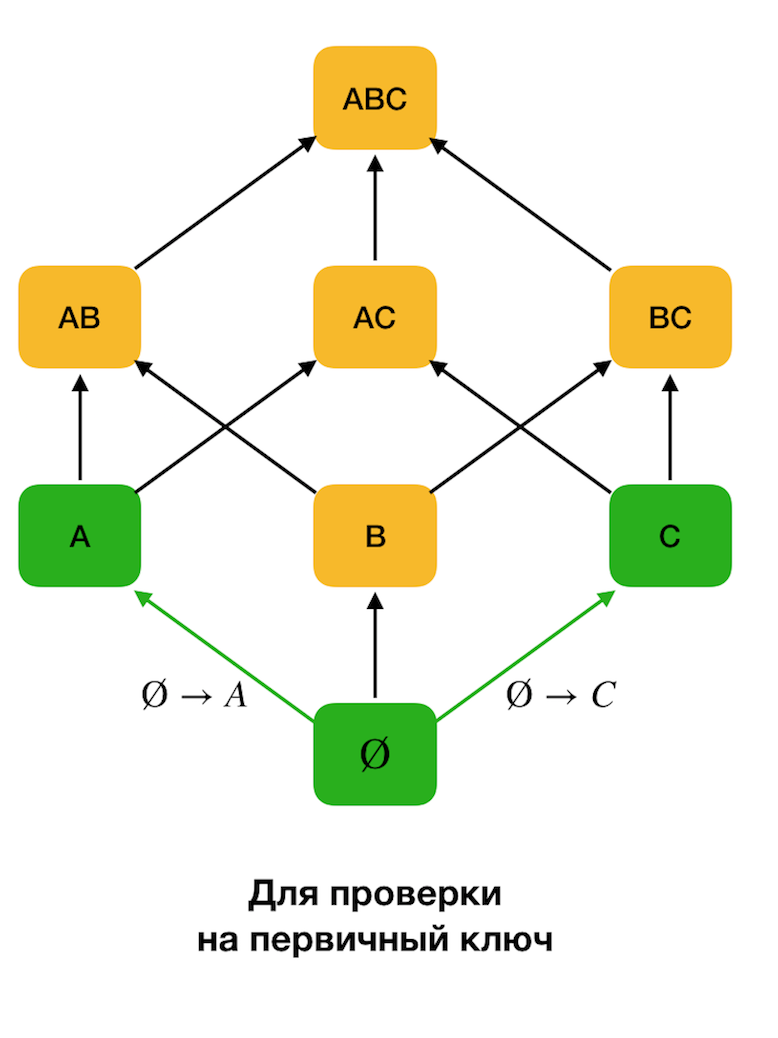
Zu Beginn werden die Abhängigkeiten der Form ∅ → Einzelattribut berücksichtigt. In diesem Schritt können Sie bestimmen, welche Attribute Primärschlüssel sind (es gibt keine Determinanten für solche Attribute, und daher ist die linke Seite leer). Ferner bewegen solche Algorithmen das Gitter nach oben. Es ist anzumerken, dass das Gitter nicht alle umgangen werden kann, dh wenn die gewünschte maximale Größe des linken Teils an den Eingang übertragen wird, geht der Algorithmus nicht über das Niveau mit dieser Größe hinaus.

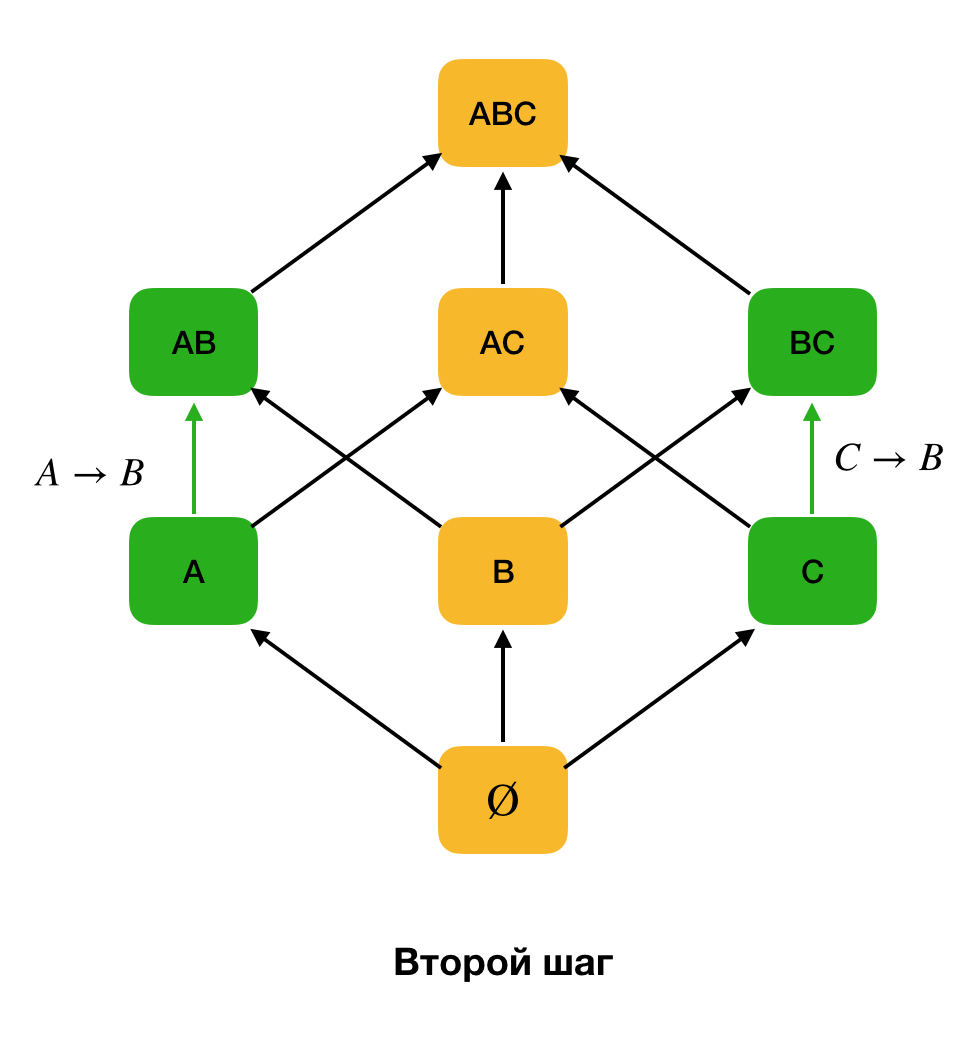
Die folgende Abbildung zeigt, wie Sie das algebraische Gitter im Suchproblem für das Bundesgesetz verwenden können. Hier repräsentiert jede Kante ( X, XY ) eine Abhängigkeit X → Y. Zum Beispiel haben wir die erste Ebene durchlaufen und wissen, dass die Abhängigkeit A → B erhalten bleibt (wir werden dies durch die grüne Verbindung zwischen den Eckpunkten A und B anzeigen). Wenn wir das Gitter nach oben bewegen, können wir daher die Abhängigkeit A, C → B nicht überprüfen, da sie nicht mehr minimal ist. Ebenso würden wir es nicht testen, wenn die Abhängigkeit C → B beibehalten würde.




Darüber hinaus verwenden in der Regel alle modernen FZ-Suchalgorithmen eine solche Datenstruktur als Partition (gestrippte Partition [1] in der Originalquelle). Die formale Definition der Partition lautet wie folgt:

Definition 6. Sei X ⊆ R die Menge der Attribute für die Beziehung r. Ein Cluster ist eine Menge von Tupelindizes aus r, die denselben Wert für X haben, dh c (t) = {i | ti [X] = t [X]}. Partition ist eine Gruppe von Clustern mit Ausnahme von Clustern mit Längeneinheiten:

$$

$$\ pi (X): = \ {c (t) | t \ in r \ wedge | c (t) | > 1 \}$$

In einfachen Worten ist die Partition für Attribut X eine Reihe von Listen, wobei jede Liste Zeilennummern mit denselben Werten für X enthält. In der modernen Literatur wird eine Struktur, die Partitionen darstellt, als Positionslistenindex (PLI) bezeichnet. Cluster mit Einheitenlänge werden für die PLI-Komprimierung ausgeschlossen, da es sich um Cluster handelt, die nur eine Datensatznummer mit einem eindeutigen Wert enthalten, der immer einfach festzulegen ist.

Betrachten Sie ein Beispiel. Kehren wir mit Patienten zur gleichen Tabelle zurück und erstellen Partitionen für die Spalten Patient und Paul (links wurde eine neue Spalte angezeigt, in der die Zeilennummern der Tabelle markiert sind):





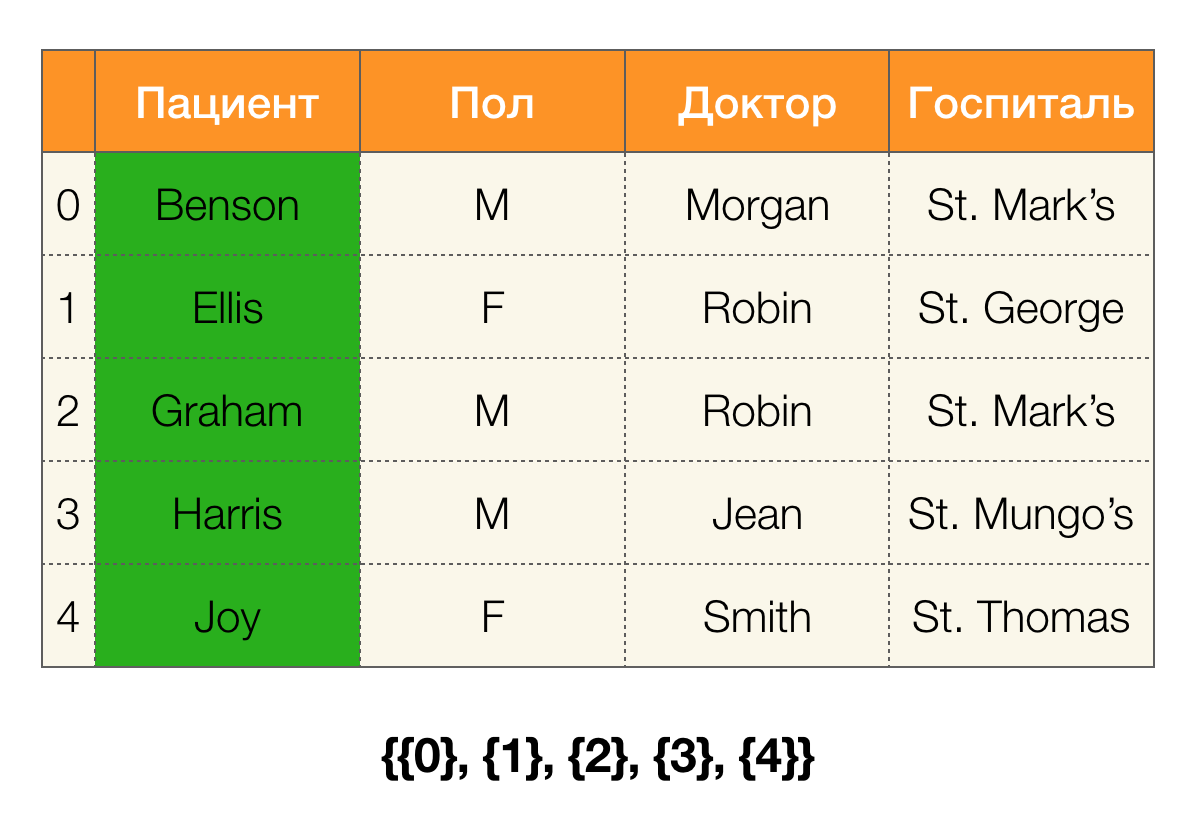
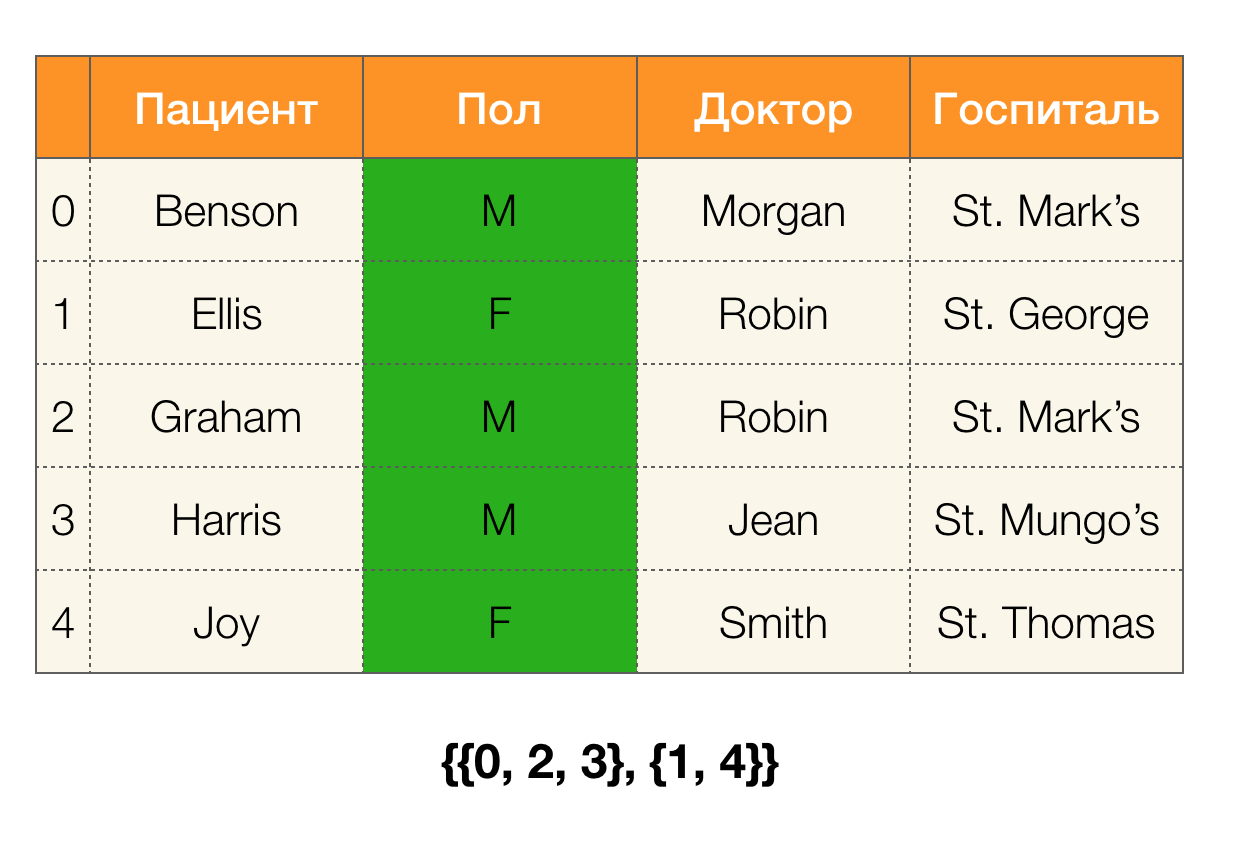
Darüber hinaus ist gemäß der Definition die Partition für die Spalte Patient tatsächlich leer, da einzelne Cluster von der Partition ausgeschlossen sind.

Partitionen können durch mehrere Attribute erhalten werden. Und dafür gibt es zwei Möglichkeiten: Durchsuchen Sie die Tabelle, erstellen Sie eine Partition auf einmal gemäß allen erforderlichen Attributen oder erstellen Sie sie mithilfe der Operation, Partitionen entlang einer Teilmenge von Attributen zu kreuzen. FZ-Suchalgorithmen verwenden die zweite Option.

Mit einfachen Worten, um beispielsweise eine Partition nach ABC- Spalten zu erhalten, können Sie Partitionen für AC und B (oder einen anderen Satz disjunkter Teilmengen) nehmen und diese miteinander schneiden. Die Operation der Schnittmenge zweier Partitionen identifiziert Cluster mit der größten Länge, die beiden Partitionen gemeinsam ist.

Schauen wir uns ein Beispiel an:





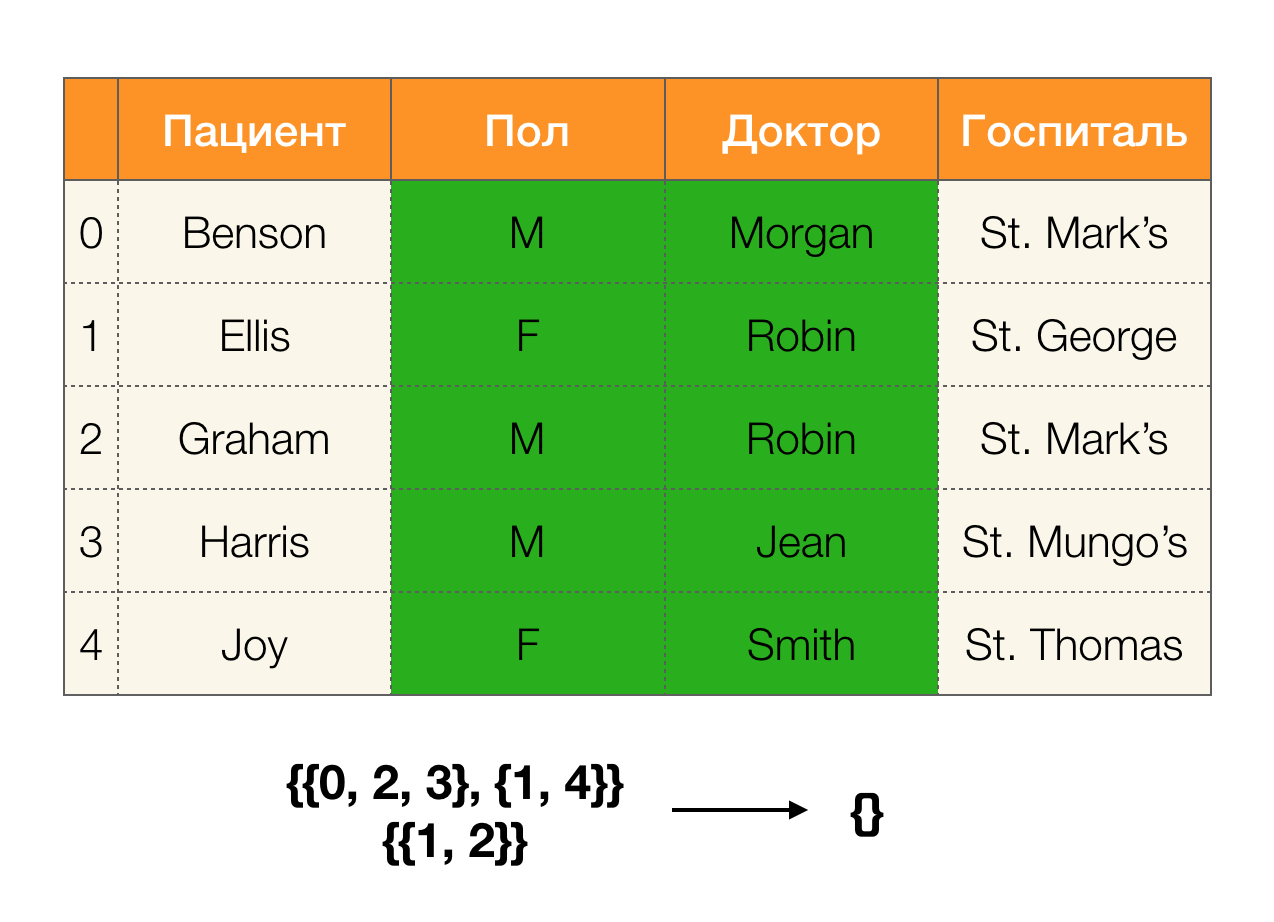
Im ersten Fall haben wir eine leere Partition erhalten. Wenn Sie sich die Tabelle genau ansehen, sind die identischen Werte für die beiden Attribute tatsächlich nicht vorhanden. Wenn wir die Tabelle geringfügig ändern (der Fall rechts), erhalten wir bereits einen nicht leeren Schnittpunkt. Gleichzeitig enthalten die Zeilen 1 und 2 tatsächlich dieselben Werte für die Attribute Paul und Doctor .

Als nächstes benötigen wir ein Konzept wie die Partitionsgröße. Formal:

$$

$$| \ pi (X) | = | \ {c \ in \ pi (X): | c | > 1 \} |$$

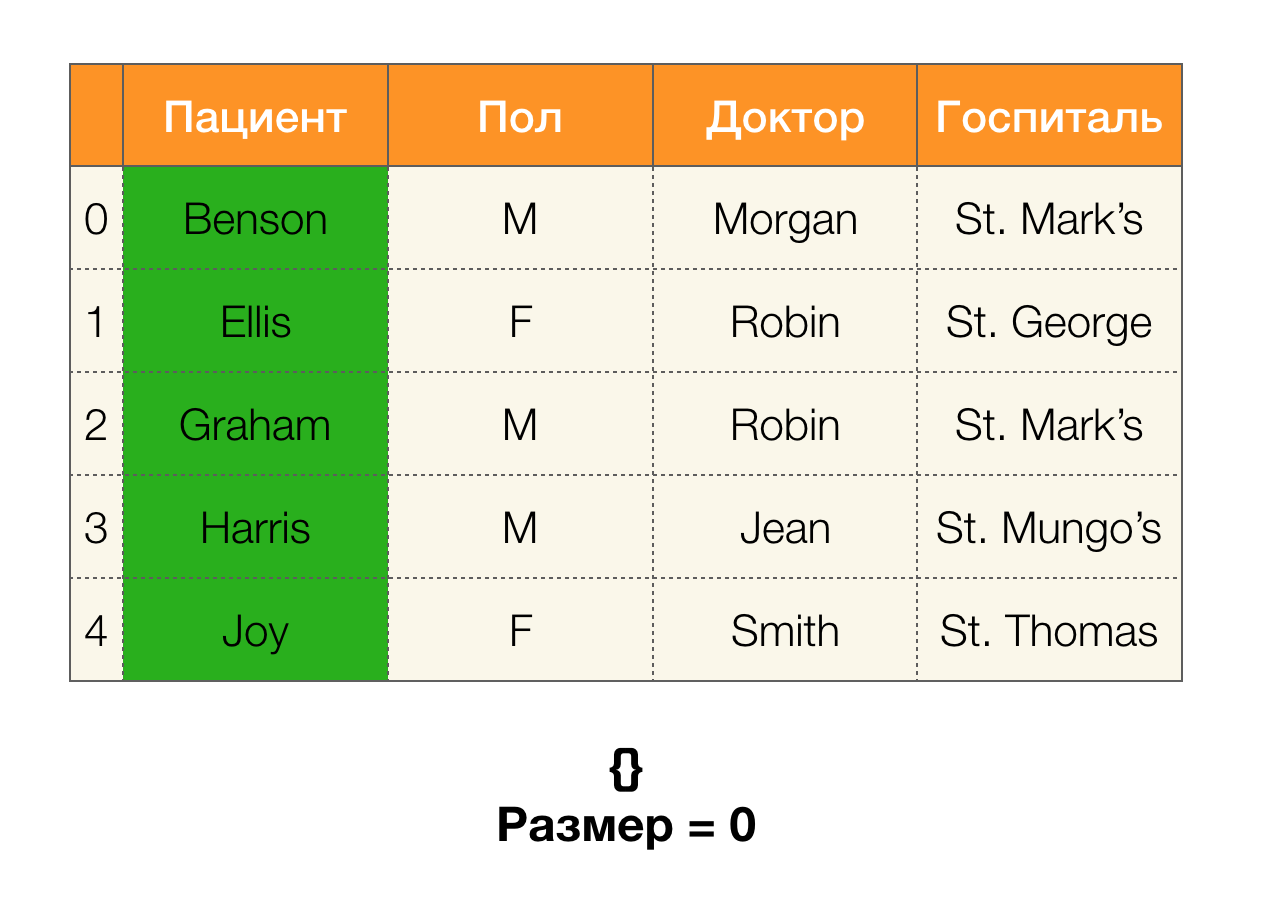
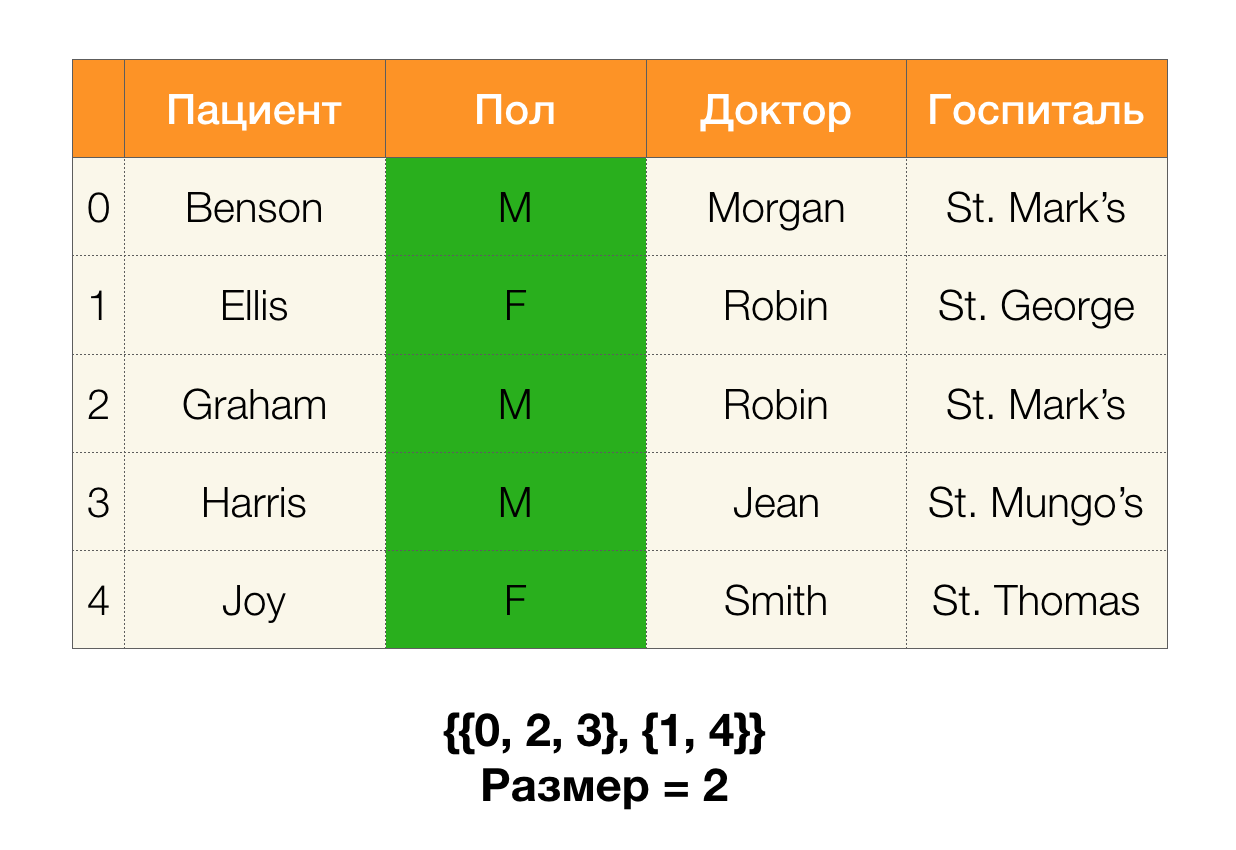
Einfach ausgedrückt ist die Partitionsgröße die Anzahl der in der Partition enthaltenen Cluster (denken Sie daran, dass einzelne Cluster nicht in der Partition enthalten sind!):





Jetzt können wir eines der Schlüssel-Lemmas definieren, mit denen wir für bestimmte Partitionen feststellen können, ob die Abhängigkeit besteht oder nicht:

Lemma 1 . Die Abhängigkeit A, B → C bleibt genau dann bestehen

$$

$$| \ pi (AB) | = | \ pi (AB \ cup \ {C \}) |$$

Nach dem Lemma müssen vier Schritte ausgeführt werden, um festzustellen, ob eine Abhängigkeit besteht.

1. Berechnen Sie die Partition für die linke Seite der Abhängigkeit
2. Berechnen Sie die Partition für die rechte Seite der Abhängigkeit
3. Berechnen Sie das Produkt aus dem ersten und zweiten Schritt
   
4. Vergleichen Sie die Größen der im ersten und dritten Schritt erhaltenen Partitionen
   

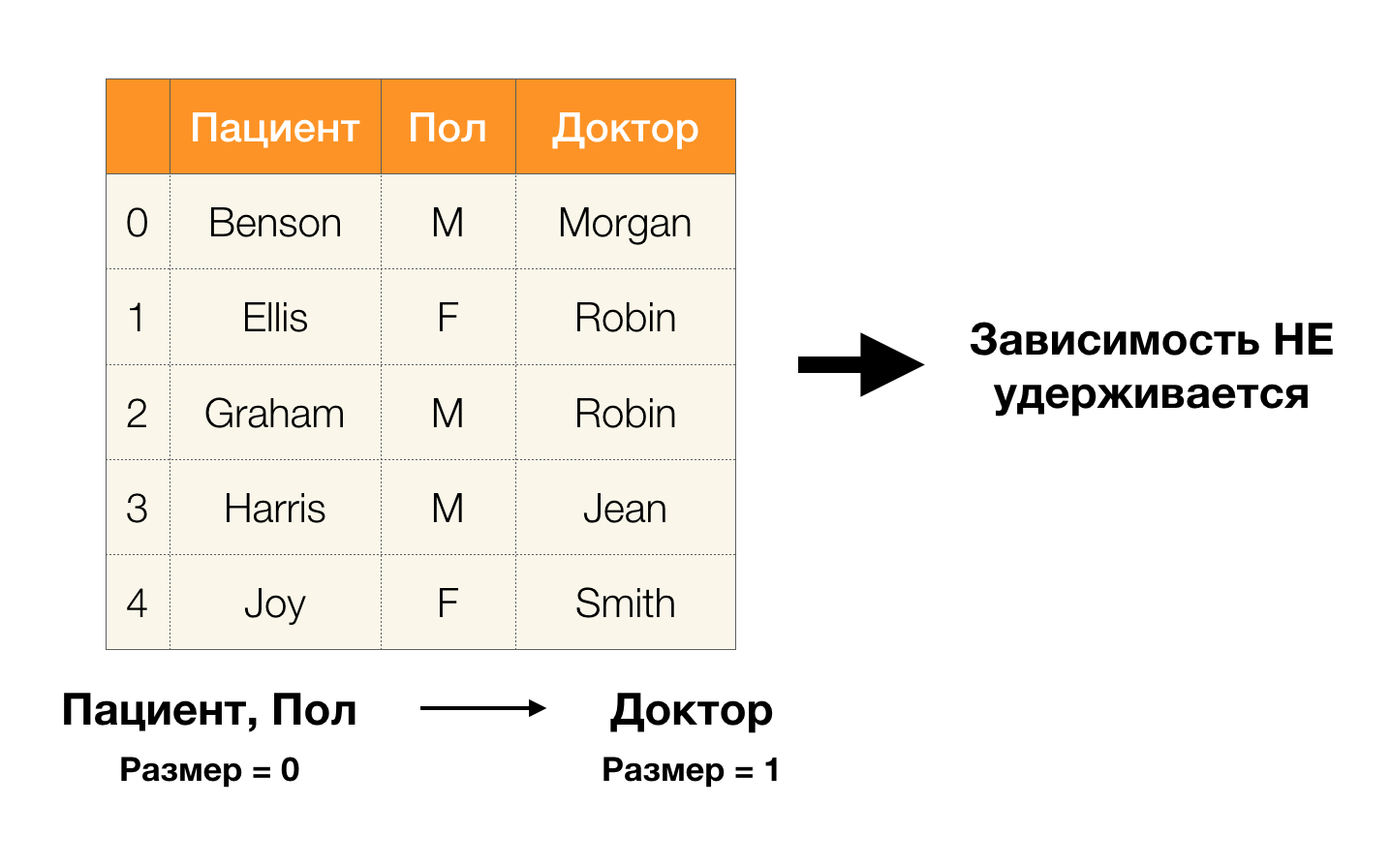
Das Folgende ist ein Beispiel für die Überprüfung, ob die Abhängigkeit durch dieses Lemma aufrechterhalten wird:






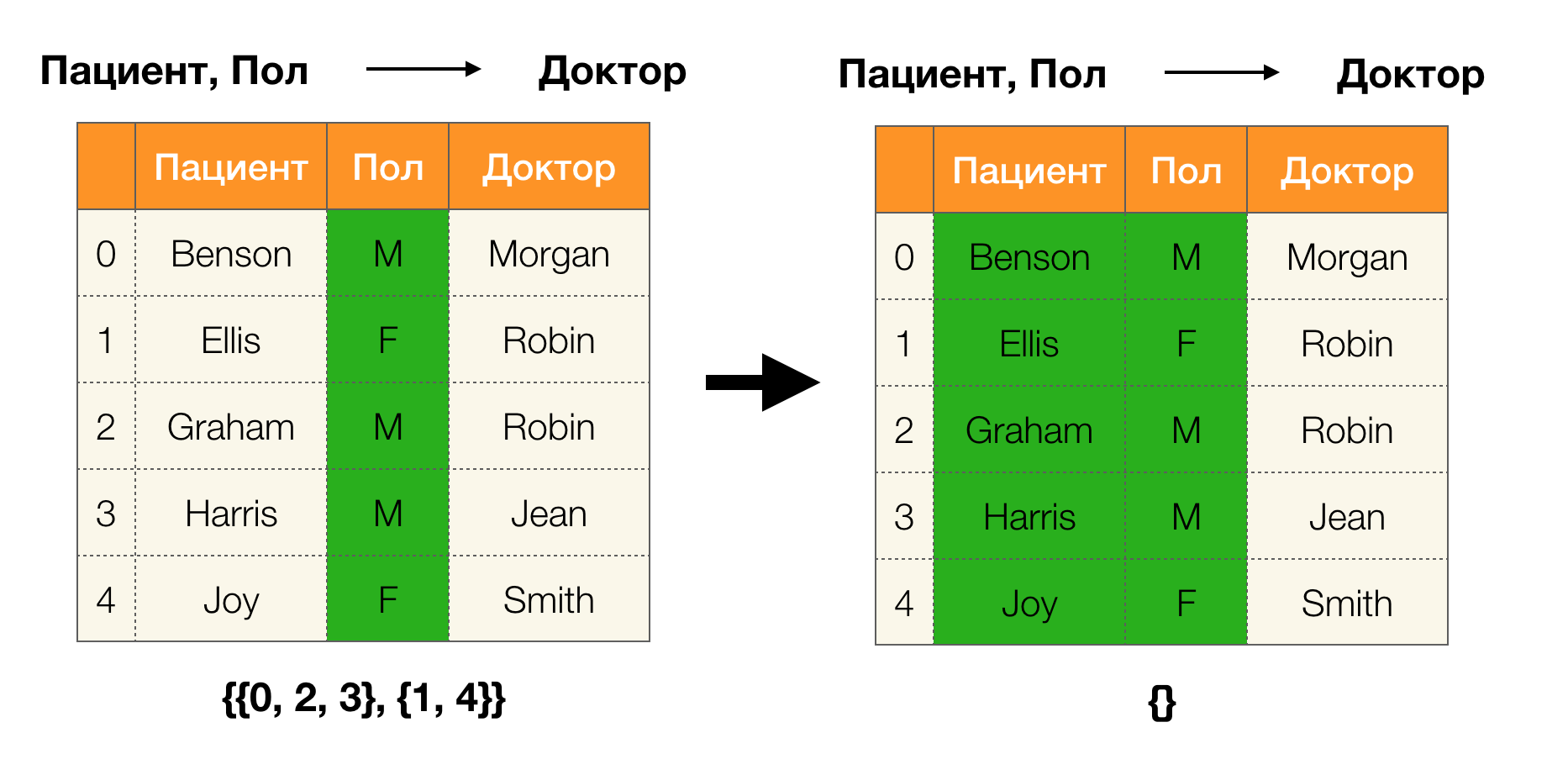
In diesem Artikel haben wir Konzepte wie funktionale Abhängigkeit, ungefähre funktionale Abhängigkeit untersucht, untersucht, wo sie verwendet werden und welche Suchalgorithmen für das Bundesgesetz existieren. Wir haben auch die grundlegenden, aber wichtigen Konzepte, die in modernen Algorithmen zur Suche nach Bundesgesetzen aktiv verwendet werden, eingehend untersucht.

Literaturhinweise:

1. Huhtala Y. et al. TANE: Ein effizienter Algorithmus zum Erkennen funktionaler und ungefährer Abhängigkeiten // Das Computerjournal. - 1999. - T. 42. - Nr. 2. - S. 100-111.
2. Kruse S., Naumann F. Effiziente Entdeckung von ungefähren Abhängigkeiten // Verfahren der VLDB-Stiftung. - 2018. - T. 11. - Nr. 7. - S. 759-772.
3. Papenbrock T., Naumann F. Ein hybrider Ansatz zur Entdeckung funktionaler Abhängigkeiten // Proceedings of the 2016 International Conference on Management of Data. - ACM, 2016 - S. 821-833.
4. Papenbrock T. et al. Funktionale Abhängigkeitsentdeckung: Eine experimentelle Bewertung von sieben Algorithmen // Verfahren der VLDB-Stiftung. - 2015. - T. 8. - Nr. 10. - S. 1082-1093.
5. Kumar A. et al. Beitreten oder nicht beitreten ?: Überlegen Sie sich zweimal, ob Sie beitreten möchten, bevor Sie Features auswählen. // Bericht der Internationalen Konferenz über Datenmanagement 2016. - ACM, 2016 - S. 19-34.
6. Abo Khamis M. et al. Datenbankinternes Lernen mit spärlichen Tensoren // Vorträge des 37. ACM SIGMOD-SIGACT-SIGAI-Symposiums zu Prinzipien von Datenbanksystemen. - ACM, 2018 - S. 325-340.
7. Hellerstein JM et al. Die MADlib-Analysebibliothek: oder MAD-Kenntnisse, die SQL // -Verfahren der VLDB-Stiftung. - 2012. - T. 5. - Nr. 12. - S. 1700-1711.
8. Qin C., Rusu F. Spekulative Näherungen für die Optimierung des teraskalen verteilten Gradientenabfalls // Ergebnisse des vierten Workshops zur Datenanalyse in der Cloud. - ACM, 2015. - S. 1.
9. Meng X. et al. Mllib: Maschinelles Lernen in Apache Spark // Das Journal of Machine Learning Research. - 2016. - T. 17. - Nr. 1 .-- S. 1235-1241.

Autoren des Artikels: Anastasia Birillo , Forscherin bei JetBrains Research , Studentin am CS-Zentrum und Nikita Bobrov , Forscherin bei JetBrains Research