Etwas mehr als ein Jahr ist vergangen, seit das MIT die Veröffentlichung der Hochleistungs-Allzwecksprache Julia angekündigt hat. Seitdem hat die Sprache an Popularität gewonnen: Sie wird an mehr als 1.500 Universitäten verwendet (in einigen wird sie als erste Unterrichtssprache unterrichtet), und die Anwendungsbereiche reichen von der medizinischen Diagnostik über die Planung von Weltraummissionen bis hin zu dringenden Problemen wie der Optimierung des Schulbusverkehrs .
Es ist nicht schwer zu erraten, dass maschinelles Lernen eines der Haupttätigkeitsfelder vieler Projekte ist, für das Julia über viele leistungsstarke Werkzeuge verfügt. Kürzlich wurde ein ziemlich interessantes Projekt veröffentlicht - das Allgemeine Wahrscheinlichkeitsprogrammiersystem „GEN“ .
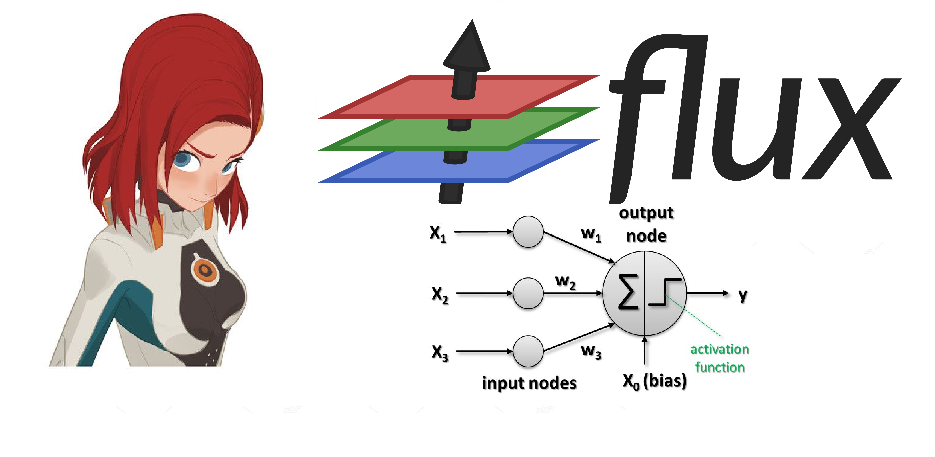
Heute werden wir, wie der Name schon sagt, auf das Flux- Paket achten, das die gesamte Leistung neuronaler Netze bietet. Wir werden versuchen, von der Verarbeitung und Erforschung von Bildsätzen zu einem trainierten neuronalen Netzwerk überzugehen, um einen vollständigen Klassifikator zu erhalten!
Installation
Laden Sie das Distributionskit von der offiziellen Website herunter und installieren Sie den Julia-Interpreter ( REPL ) auf Ihrem Computer.
Damit der Paketmanager ordnungsgemäß funktioniert, müssen Benutzer von Windows 7 / Windows Server 2012 außerdem Folgendes installieren:
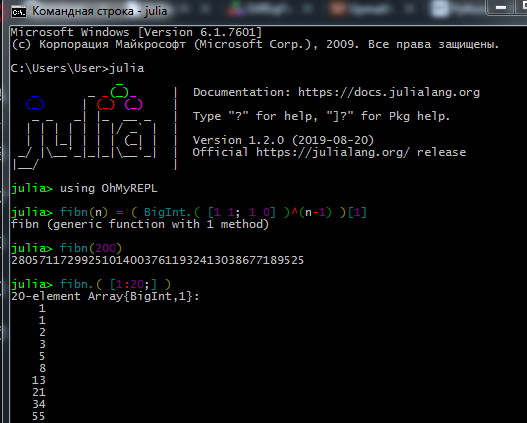
Der Prozess der Arbeit in REPL sieht ungefähr so aus:
Echte Datasayantisten und Maschinenlingologen bevorzugen Jupyter . Hier können Sie sich über die Installation informieren und interaktive Lektionen zum Selbststudium mit Aufgaben in Russisch finden (Links zu Original-Tutorials und eine Anleitung zur dortigen Sprache).
Hier sehen Sie, wie Sie mit dem Jupyter Notebook arbeiten.
Bei Installationsproblemen- Verbindung kann nicht hergestellt werden - überprüfen Sie Ihre Zugriffsrechte (haben Sie Einschränkungen beim Schreiben in Ordner unter C: \, melden Sie sich als Administrator an oder starten Sie Julia im Administratormodus). Wenn Sie einen Proxy verwenden, stellen Sie sicher, dass dieser nicht nur für den Browser konfiguriert ist
- Einige Pakete mögen das kyrillische Alphabet im Dateipfad nicht, daher hatte ich aufgrund des Benutzernamens auf Russisch viele Probleme
- Wenn das Interact- Paket keine Ergebnisse anzeigt, haben Sie WebIO möglicherweise falsch installiert, was behoben werden kann
- Damit einige Pakete unter Windows ordnungsgemäß funktionieren, müssen die Pfade zu Julia und Jupyter in Umgebungsvariablen eingegeben werden.
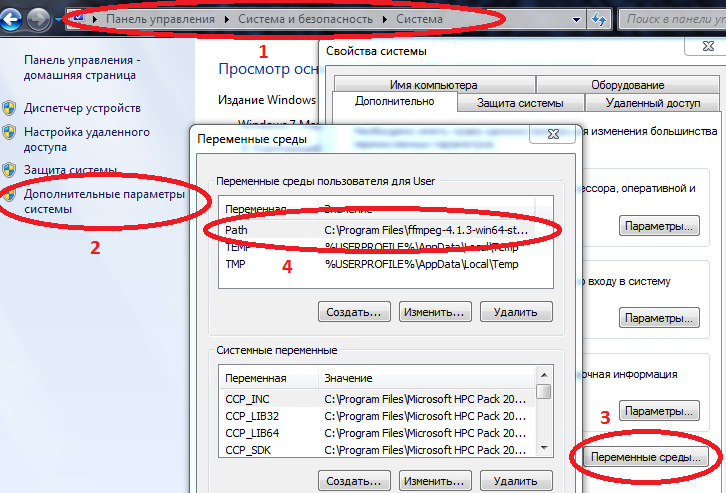
Computer / Systemeigenschaften / Erweiterte Systemparameter / Umgebungsvariablen / Pfad (Erstellen, falls nicht) und fügen Sie dort den Pfad zu julia.exe hinzu
Beispiel C: \ Benutzer \ Benutzer \ AppData \ Local \ Julia-1.2.0 \ bin
Wenn Path bereits Werte hat, trennen Sie diese mit einem Semikolon.
Wenn Sie nun julia in die Befehlskonsole ( cmd ) fahren, wird der Interpreter gestartet.
Nachdem Sie alles installiert haben, was Sie benötigen, können Sie die heute benötigten Pakete herunterladen. Geben Sie Befehle in REPL oder Jupyter ein
Code using Pkg pkgs = ["Plots", "TextParse", "CSV", "DataFrames", "ImageMagick", "Images", "Interact", "Flux"] for p in pkgs Pkg.add(p) end for p in pkgs Pkg.build(p) end
Nachdem Sie die Grundlagen der Sprache gelernt haben (Arbeiten mit Arrays, Erstellen von Funktionen, Herunterladen von Paketen, Zeichnen von Diagrammen), können Sie mit dem nachfolgenden Material fortfahren.
Laden und Verarbeiten von Daten
Das Sammeln und Organisieren von Daten ist eine separate Kunst. In Bezug auf Julia hat das Netzwerk viel veraltetes Material, aber für den Anfang können Sie das obige Tutorial ausprobieren und für eine gründlichere Studie das Buch Data Science with Julia (gemeinfrei) lesen.
Und heute werden wir vielleicht mit bereits vorbereiteten Daten arbeiten: einem Datensatz aus einer Vielzahl von Fotos von Früchten aus verschiedenen Blickwinkeln - wer wollte eine frische Frucht?


Eigentlich ist dies die Aufgabe - wir werden dem neuronalen Netz beibringen, Äpfel von Bananen zu unterscheiden!
Laden Sie zuerst einige Testbilder hoch:
using Images fnames = [ "data/10_100.jpg", "data/107_100.jpg", "data/yellow_apple_2.jpg", "data/8_100.jpg", "data/104_100.jpg", "data/3_100.jpg" ]

Wie unterscheiden sich die Objekte auf den Bildern voneinander? Erstens nach Form, zweitens nach Farbe und dann nach Texturen und anderen Attributen. Die Bildanalyse ist an sich ein interessantes Thema, und die Klassifizierung kann nicht nur von Neuronen, sondern beispielsweise auch von Wavelets vorgenommen werden . Wir beginnen mit der einfachsten Zeichenfarbe.
Wie Sie wissen, werden Bilder in Form von Arrays im Computerspeicher gespeichert. In unserem Fall handelt es sich um Matrizen, von denen jede Zelle drei Zahlen enthält, die die Mengen an roten, grünen und blauen Farben in jedem Pixel des Bildes angeben. Sehen wir uns die durchschnittliche Menge jeder Farbe in diesen Bildern an:
using Statistics: mean M1 = [ mean(float.(c.(img))) for c = [red,green,blue], img = fruits ] 3×6 Array{Float32,2}: 0.570278 0.652852 0.977111 0.835252 0.903998 0.842564 0.338118 0.468729 0.950773 0.806882 0.880692 0.755442 0.322406 0.379424 0.835212 0.707626 0.799643 0.761916
Wir schauen uns die erste Zeile genau an - stört es Sie nicht? Ein gelber Apfel und Bananen sind roter als Äpfel der Sorte Breburn! Wie so ?! Komm schon, mach saure Minen, vielleicht lesen die Schüler dieses Tutorial oder jüngere Schüler vom Ballett- und Traktorinstitut. Daher werden wir versuchen, Auslassungen zu vermeiden. Tatsache ist, dass der Hintergrund jedes Bildes weiß ist und in der RGB- Notation durch die Werte (1,1,1) dargestellt wird. Und da die 3 Strichbilder mehr 6 Hintergründe enthalten und die Farbe der Bananen und des gelben Apfels auch Rot enthält, stellt sich heraus, dass die ersten beiden Bilder rot verlieren. Aus Gründen der Übersichtlichkeit teilen wir die Bilder in Grundfarben auf:
function tweaking(img) R = colorview( RGB, red.(img),zeroarray,zeroarray ) G = colorview( RGB, zeroarray,green.(img),zeroarray ) B = colorview( RGB, zeroarray,zeroarray, blue.(img) ) [R; G; B] end tweaking( hcat(fruits...) )

Haben Sie jemals das kryptische Wort "Basis" gehört? Wir können also sagen, dass diese Bilder auf RGB- Basis angelegt sind. Je schwärzer - desto weniger eine bestimmte Farbe, und wie wir erwartet haben, macht der Hintergrund mit seinem Reichtum die Berechnung der Durchschnittswerte verrauscht. Löschen Sie es.
function remove_background(img) mtrx = copy( channelview(img) ) for i = 1:size(mtrx, 2), j = 1:size(mtrx, 3) if reduce(&, mtrx[:,i,j] .> [0.8, 0.8, 0.8])

M3 = [ mean(float.(c.(img))) for c = [red,green,blue], img = greyfruits ] 3×6 Array{Float32,2}: 0.451008 0.532696 0.578967 0.527727 0.52849 0.500276 0.218805 0.348609 0.552679 0.499192 0.505136 0.412946 0.203528 0.260142 0.439354 0.400631 0.424784 0.419291
Der Unterschied in der Fläche, die von jedem Objekt eingenommen wird, wirkt sich immer noch aus, aber im Allgemeinen kann geschlossen werden, dass Bananen grünere ( und blaue ) Äpfel sind. Dies wird das Bewertungskriterium sein, das heißt - ein Zeichen. Schauen wir uns nun den Rest der Bilder an:
pth = "C:\\Users\\User\\Desktop\\Banana"
Für jedes Bild neutralisieren wir den Beitrag des Hintergrunds, ermitteln die durchschnittliche Menge jeder Farbe und merken uns gleichzeitig die Größe der Bilder ...
dataz = [] for fname in fnames img_i = load("$pth\\$fname") gbimg = remove_background(img_i) colorz = [ mean(c.(gbimg)) for c = [red,green,blue] ] inform = [size(gbimg, 1) size(gbimg, 2) colorz' ] push!(dataz, inform) end dataz
... und dann können Sie unsere Daten in arbeitsfähigen Strukturen anordnen - Datenrahmen:
using DataFrames, CSV banans = DataFrame( vcat(dataz...), [:height, :width, :red, :green, :blue] ) CSV.write("data/bananas.csv", banans)
apples = CSV.read("data/Apple_Braeburn.csv")
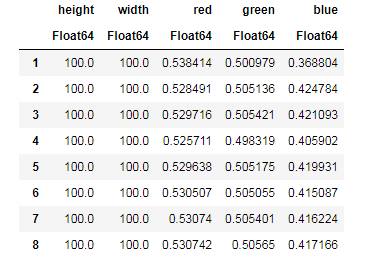
Desc = describe(apples, :all)
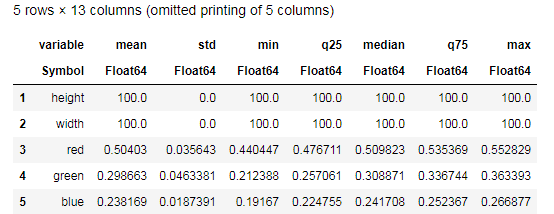
Versuchen Sie, die von der Funktion description describe() bereitgestellten Daten zu verstehen und mit einer ähnlichen Tabelle für Bananen zu vergleichen. Was für eine Datenanalyse kann ohne Grafiken sein?
function plot2features(clr) x_apples = apples[:, :green] x_banans = banans[:, :green] y_apples = apples[:, clr] y_banans = banans[:, clr] scatter(x_apples, y_apples, lab = "apples", colour = :red) scatter!(x_banans, y_banans, lab = "bananas", legend = :topleft, colour = :yellow) hline!([mean(y_apples), mean(y_banans) ], lab = "" ) vline!([mean(x_apples), mean(x_banans) ], lab = "" ) xaxis!("green") yaxis!("$clr") end plot2features(:red)
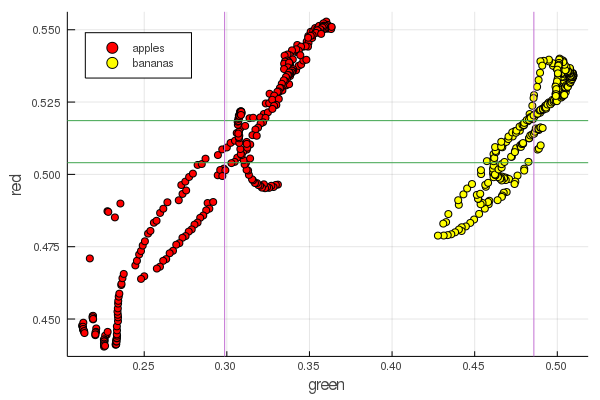
plot2features(:blue)
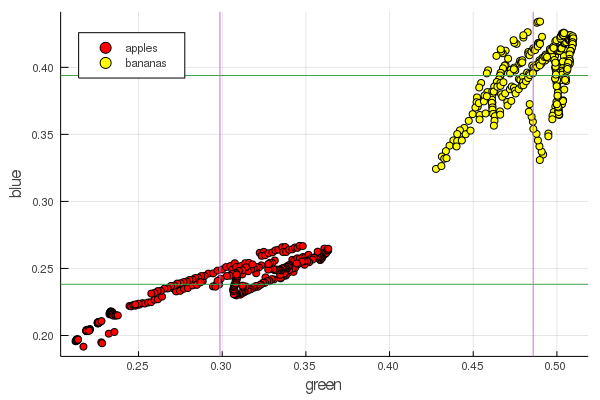
Mittelbananenrot hat einen sehr ähnlichen Wert wie Mittelapfelrot. In der zweiten Tabelle wird die Isolierung von Früchten jedoch sofort deutlicher durch zwei Farbmerkmale gleichzeitig verfolgt. Trennungen können durch korrekte Renormierung verbessert werden. Beispielsweise ändern sich unsere Grünwerte von 0,2 auf 0,55, und wenn Sie die Konvertierung durchführen
dann werden die Daten um [0,1] neu skaliert, wodurch sich die Lücke zwischen diesen vergrößert Haufen Cluster von Punkten.
Perceptron
Die Klassifizierungsaufgabe besteht darin, ein Modell zu definieren und Parameter auszuwählen, für die verschiedene Daten eindeutig eine Bewertung ihrer Zugehörigkeit zu einer bestimmten Klasse erhalten. Einfach ausgedrückt, müssen wir eine bestimmte Funktion einführen und ihre Parameter so einstellen, dass sie unsere Äpfel von Bananen trennt.
Das bekannteste und beliebteste Modell für diese Zwecke ist das künstliche Neuron McCulloch-Pitts, das Anfang der 1940er Jahre entwickelt wurde. Anschließend schlug Frank Rosenblatt ein trainiertes neuronales Netzwerk vor - das Perzeptron. Es ist nicht schwierig, umfassende Erklärungen zu neuronalen Netzen zu finden, auch zu dieser Ressource (z. B. Neuronale Netze für Anfänger , Verwendung neuronaler Netze bei der Bilderkennung , Neuronale Netze, grundlegende Funktionsprinzipien, Vielfalt und Topologie ).
Auswahl des Sigmoid als Aktivierungsfunktion und Einstellung der Ausgänge der klassifizierten Objekte (Früchte) entsprechend ihren Ausgängen
Wählen Sie solche Parameter und so dass die Ausgabewerte des Sigmoid für die empfangenen Daten der obigen Notation entsprechen
using Interact sigmo(x,w,b) = 1 / (1 + exp(-w*x+b)) r_apples, g_apples, b_apples = apples[:, :red], apples[:, :green], apples[:, :blue] r_banans, g_banans, b_banans = banans[:, :red], banans[:, :green], banans[:, :blue]; @manipulate for w in 10:1:60, b in -5:1:25 plot(x->sigmo(x,w,b), 0, 1, label="Model", legend = :topleft, lw=3) scatter!(g_apples[1:5], zeros(10), label="Apple", colour = :red) scatter!(g_banans[1:5], ones(10), label="Banana", colour = :yellow) end
foon(x) = sigmo(x,60,24) plot(foon, 0, 1, label="Model", legend = :topleft, lw=3) scatter!(foon, g_apples, label="Apple", colour = :red) scatter!(foon, g_banans, label="Banana", colour = :yellow) xaxis!("green")
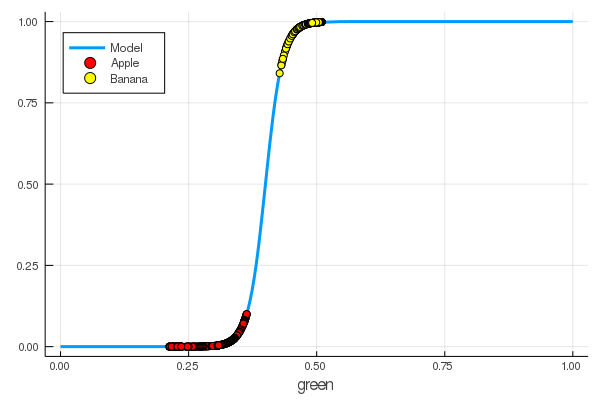
Wir haben einem Neuron manuell beigebracht, Äpfel von Bananen anhand der Menge an Grün zu unterscheiden!
Natürlich der Wunsch, diesen Prozess zu automatisieren. Wir führen die Verlustfunktion ein
Jetzt besteht der Lernprozess darin, diese Funktion zu minimieren :
Code apples_mean_green = mean(g_apples) banans_mean_green = mean(g_banans) L(w, b) = (0 - sigmo(apples_mean_green,w,b))^2 + (1 - sigmo(banans_mean_green,w,b))^2 w_range = 10:0.5:30 b_range = 0:0.5:20 L_values = [L(w,b) for b in b_range, w in w_range] @manipulate for w in w_range, b in b_range p1 = surface(w_range, b_range, L_values, xlabel="b", ylabel="w", cam=(80,40), cbar=false, leg=false) scatter!(p1, [w], [b], [L(w,b)+1e-2], markersize=5, color = :blue) p2 = plot(x->sigmo(x,w,b), 0, 1, label="Model", legend = :topleft, lw=3) scatter!(p2, [apples_mean_green], [0.0], label="Apple", markersize=10) scatter!(p2, [banans_mean_green], [1.0], label="Banana", markersize=10, xlim=(0,1), ylim=(0,1)) plot(p1, p2, layout=(2,1)) end
Zuvor haben wir Pakete für Julia untersucht , mit denen Optimierungsprobleme mit verschiedenen Methoden gelöst werden können. Zum Glück ist das Wesentliche bereits in der Flux-Umgebung enthalten!
Flussmittel
using Flux
Zunächst präsentieren wir die Daten für das Training in verdaulicher Form:
Y = [zeros(length(g_apples)); ones(length(g_banans)) ] |> permutedims X = [g_apples; g_banans] |> permutedims;
Weiter in der Reihenfolge:
- Wir erstellen einen Trainingsdatensatz, indem wir die Eingabedaten mit den richtigen Antworten bezüglich der Klassifizierung dieser Daten kombinieren
- Wir setzen die Parameter W und b durch Matrizen von Zufallswerten (es gibt ein Vorzeichen am Eingang und eines am Ausgang, also sind die Matrizen 1 x 1 groß).
- Als Modell setzen wir eine dichte Schicht - ein Perzeptron mit einer sigmoidalen Aktivierungsfunktion
- Wir setzen die Verlustfunktion - die Summe der quadratischen Differenzen (Sie können immer noch die populärere
Flux.crossentropy() ). - Als Optimierungsmethode wählen wir den Gradientenabstieg . Es braucht einen Parameter - Abstiegsgeschwindigkeit
- Wir legen eine Bewertungsfunktion fest, die die Werte der Modellausgaben rundet und mit den richtigen Antworten vergleicht.
- Und drucken Sie die Parameter unseres ungeübten Modells aus
dataz = [(X, Y)] W = param(rand(1)) b = param(rand(1)) model = Dense(W, b, σ) loss(x, y) = mse(model(x), y) opt = Descent(0.1) accuracy(x, y) = mean( round.(model(x)) .== y ) params(model) Params([[0.3372841444115968] (tracked), [0.8430399003786011] (tracked)])
Mal sehen, was die Ausgabe der Verlustfunktion für unsere Daten ist.
loss(X, Y)
Und überprüfen Sie die Ergebnisse der Bewertungsfunktion
accuracy(X, Y) 0.5
Das Ergebnis ist ganz natürlich - die Ausgaben sind ziemlich gleichmäßig verteilt und die Hälfte der Daten ist korrekt klassifiziert:
Code modeldataz(x) = x |> model |> data |> permutedims
modelX = modeldataz(X) modelapples = modeldataz(g_apples') modelbanans = modeldataz(g_banans') plot(modelX, legend = false) hline!([0.5]) p1 = yaxis!((0,1)) curv = [-1:0.01:1;]' |> modeldataz plot( [-1:0.01:1;], curv, label="Model", legend = :topleft, lw=3) scatter!(g_apples, modelapples, label="Apple", colour = :red) scatter!(g_banans, modelbanans, label="Banana",colour = :yellow) hline!([0.5], lab = "", legend = :topleft) p2 = xaxis!("green") plot(p1, p2)
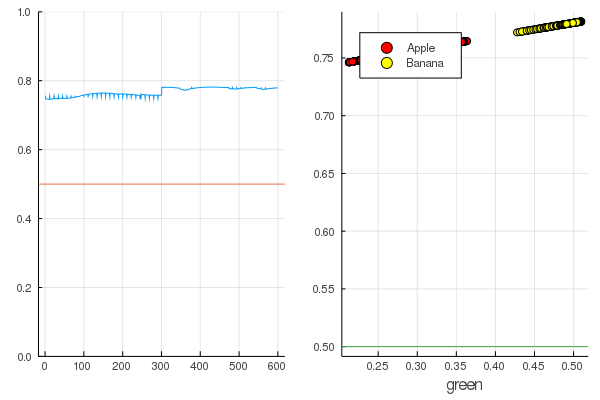
Fangen wir an: Es ist ziemlich einfach. Sie müssen nur das neuronale Netzwerk anschreien: „Trainieren!“, Während Sie angeben, worauf trainiert und was minimiert werden soll, und sie wird eine Trainingseinheit absolvieren. Deshalb werden wir sie zwingen, alles so zu entwöhnen, wie es sollte, aber nur ohne Fanatismus, damit es keine Umschulung gibt
for i in 1:7000 train!(loss, params(model), dataz, opt) end model.W, model.b ([9.578663260720564] (tracked), [-3.7540362587506464] (tracked))
Die Verluste sind viel geringer geworden:
loss(X, Y) 0.09152783090457564 (tracked)
Eine Bewertung ist besser:
accuracy(X, Y) 1.0
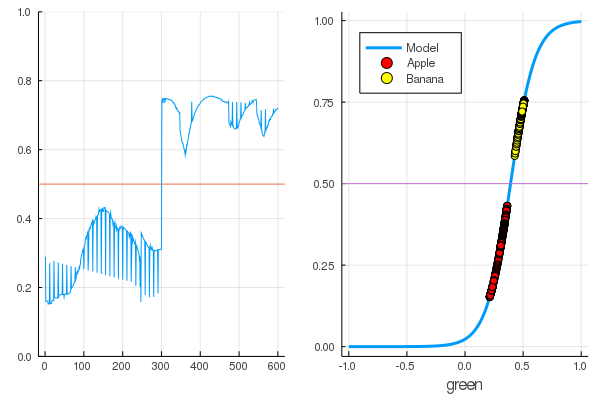
Die Daten werden geteilt, und durch weiteres Training wird das Modell vertikaler funktionieren. Überprüfen Sie das trainierte Modell auf dem ersten Satz von Früchten:
function classifier(img) gbimg = remove_background(img) greenmean = mean(float.(green.(gbimg))) answ = data( model( [ greenmean ]' ) )[1] fr = answ > 0.5 ? "Banana" : "Apple" "$fr $(round(200abs(0.5-answ)))%" end hcat(fruits...)

classifier.(fruits) 6-element Array{String,1}: "Apple 68.0%" "Apple 20.0%" "Banana 65.0%" "Banana 47.0%" "Banana 49.0%" "Banana 10.0%"
Ein speziell gepflanzter gelber Apfel wurde natürlich nicht richtig erkannt, und eine rote Banane trat kaum in ihre Kategorie ein. Aber das Neuron bekommt nur eine Zahl aus dem Bild - die durchschnittliche Menge an Grün. Sie können ein weiteres Zeichen hinzufügen, z. B. die Menge an Blau, wodurch das Modell etwas anpassungsfähiger wird.
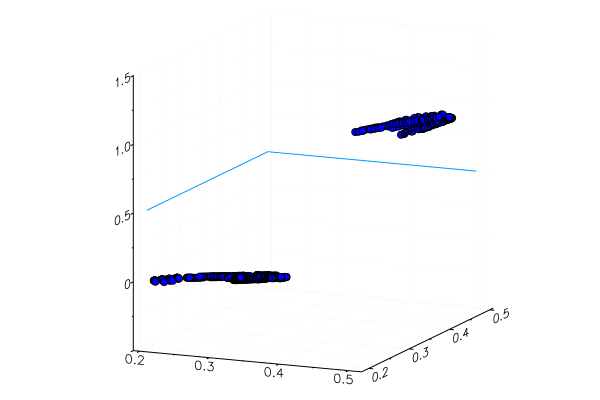
Oder Sie können nicht die RGB-Darstellung verwenden, sondern HSV (Farbton, Sättigung, Wert), in dem der Farbtonkanal Informationen über die Farbe des Bildes enthält.
Das ganze Vergnügen neuronaler Netze besteht darin, dass sie selbst Merkmale unterscheiden können, die manchmal nicht sehr offensichtlich sind (Farbkorrelation, ihre Verteilung, Umrisse und Kurven ...), und Sie können ihnen mit Hilfe spezieller Heuristiken und Techniken helfen, die die Arbeit mit neuronalen Netzen in verwandeln echte Kunst.

Damit die Führung nicht zu stark wächst und mache eine Reihe von Artikeln zu faul Lassen Sie uns auch ein Beispiel für die Klassifizierung von Bildern mit handgeschriebenen Zahlen geben, und der interessierte Leser wird das gewonnene Wissen selbst in Bilder mit Früchten verallgemeinern und sein eigenes neuronales Netzwerk erstellen, das beispielsweise Objekte in Stillleben markieren kann!
Mnist
using Images using Flux, Flux.Data.MNIST, Statistics using Flux: onehotbatch, onecold, crossentropy, throttle using Base.Iterators: repeated
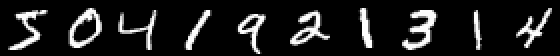
Ein Beispiel ist insofern interessant, als es bereits zehn Ausgänge gibt. Hier bieten sich sogenannte One-Hot- Vektoren an.
labels = MNIST.labels()
10×60000 Flux.OneHotMatrix{Array{Flux.OneHotVector,1}}: 0 1 0 0 0 0 0 0 0 0 0 0 0 … 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 1 0 1 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 1 0 1 0 0 0 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 1 0 … 0 0 0 0 0 1 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 1 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 1 0 1 0 0 0 0 0 0 0
Wir definieren eine Kette von Neuronen als Modell, die Kreuzentropie wird eine Verlustfunktion sein und Adam als Optimierungsmethode:
m = Chain( Dense(28^2, 32, relu), Dense(32, 10), softmax) loss(x, y) = crossentropy(m(x), y) accuracy(x, y) = mean(onecold(m(x)) .== onecold(y)) dataset = repeated((X, Y), 20) evalcb = () -> @show(loss(X, Y)) opt = ADAM()
Trainieren Sie im Sparing-Modus, drucken Sie jedoch alle 10 Sekunden Verluste aus:
for i = 1:10 Flux.train!(loss, params(m), dataset, opt, cb = throttle(evalcb, 10)) end
accuracy(X, Y) 0.64545
Und überprüfen Sie die Daten, die nicht im Training verwendet wurden
Neuronale Netze auf Julia sind einfach und sehr aufregend! Auch wenn Sie nicht nach Verbindungen zwischen Ihrem Tätigkeitsbereich und maschinellem Lernen suchen müssen, sollten Sie zumindest diese Neugier spüren, die aus allen Blickwinkeln geschrien wird, und es wird keinen Mangel an Werkzeugen geben!
Alles mäßige CPU-Hitze!