Detaillierte Analyse der Simplex-Methode

Prolog

Vor kurzem musste ein Programm von Grund auf neu erstellt werden, das den Algorithmus der Simplex-Methode implementiert. Im Verlauf der Lösung stieß ich jedoch auf ein Problem: Es gibt nicht so viele Ressourcen im Internet, in denen Sie eine detaillierte theoretische Analyse des Algorithmus (seine Begründung: warum wir diese oder jene Schritte unternehmen) und praktische Implementierungstipps - direkt den Algorithmus - einsehen können. Dann habe ich mir ein Versprechen gegeben - sobald ich die Aufgabe erledigt habe, werde ich meinen Beitrag zu diesem Thema schreiben. Eigentlich werden wir darüber reden.

Bemerkung. Der Beitrag wird in einer recht formellen Sprache verfasst, aber mit Kommentaren versehen, die Klarheit schaffen sollten. Ein solches Format wird den wissenschaftlichen Ansatz bewahren und kann gleichzeitig einigen helfen, dieses Problem zu untersuchen.

§1. Erklärung des linearen Programmierproblems

Definition: Die lineare Programmierung ist eine mathematische Disziplin, die sich der Theorie und den Methoden zur Lösung extremer Probleme auf Mengen von n-dimensionalen Räumen widmet, die durch Systeme linearer Gleichungen und Ungleichungen definiert sind.

Die allgemeine Aufgabe der linearen Programmierung (im Folgenden - LP) hat die Form:

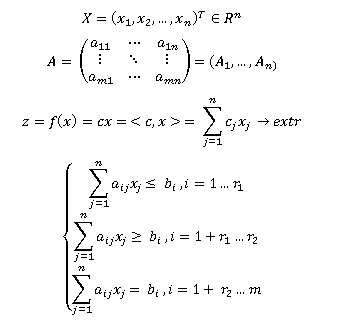
§2. Die kanonische Form des LP-Problems

Die kanonische Form des LP-Problems:



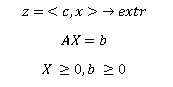Hinweis: Jedes LP-Problem wird auf kanonisch reduziert.

Der Algorithmus für den Übergang von einem beliebigen LP-Problem zur kanonischen Form:

1. Ungleichungen mit negativ$$ $ inline $ b_i $ inline $ multiplizieren Sie mit (-1).
2. Wenn eine Ungleichung der Form (≤) vorliegt, fügen Sie diese auf der linken Seite hinzu$$ $ inline $ s_i $ inline $ Ist eine zusätzliche Variable, und wir erhalten Gleichheit.
3. Wenn eine Ungleichung der Form (≥) vorliegt, subtrahieren Sie von der linken Seite$$ $ inline $ s_i $ inline $ und wir erhalten die Gleichheit.
4. Wir ersetzen Variablen:

• Wenn$$ $ inline $ x_i ≤ 0 $ inline $ dann$$ $ inline $ x_i '= -x_i ≥ 0 $ inline $
• Wenn$$ $ inline $ x_i $ inline $ - beliebig$$ $ inline $ x_i = x_i '- x_i' '$ inline $ wo$$ $ inline $ x_i ', x_i''≥ 0 $ inline $

Hinweis: Wir werden nummerieren$$ $ inline $ s_i $ inline $ durch die Ungleichungszahl, zu der wir sie hinzugefügt haben.

Hinweis:$$ $ inline $ s_i $ inline $ ≥0.

§3. Eckpunkte. Grundlegende / freie Variablen. Grundlegende Lösungen

Definition: Punkt$$ $ inline $ X ∈ D $ inline $ wird als Eckpunkt bezeichnet, wenn die Darstellung$$ $ inline $ X = αX ^ 1 + (1-α) X ^ 2, wobei X ^ 1, X ^ 2 ∈ D; 0 <α <1 $ inline $ nur möglich mit$$ $ inline $ X ^ 1 = X ^ 2 $ inline $ .

Mit anderen Worten, es ist unmöglich, zwei Punkte in der Region zu finden, deren Intervall enthält$$ $ inline $ X $ inline $ (d.h.$$ $ inline $ X $ inline $ Ist kein interner Punkt).

Die grafische Methode zur Lösung des LP-Problems zeigt, dass das Finden der optimalen Lösung mit einem Eckpunkt verbunden ist. Dies ist das Grundkonzept bei der Entwicklung einer Simplex-Methode.

Definition: Es gebe ein System von m Gleichungen und n Unbekannten (m <n). Wir teilen die Variablen in zwei Mengen: (nm) Wir setzen die Variablen gleich Null, und die verbleibenden m Variablen werden durch Lösen des Systems der Anfangsgleichungen bestimmt. Wenn diese Lösung eindeutig ist, werden Variablen ungleich Null als Basisvariablen bezeichnet. Nullvariablen (nm) - frei (nicht basisch), und die entsprechenden resultierenden Werte der Variablen werden als Basislösung bezeichnet.

§4. Simplex-Methode

Mit der Simplex-Methode können Sie effektiv die optimale Lösung finden und die einfache Aufzählung aller möglichen Eckpunkte vermeiden. Das Hauptprinzip der Methode: Die Berechnungen beginnen mit einer Art „Start“ -Basislösung, und dann wird nach Lösungen gesucht, die den Wert der Zielfunktion „verbessern“. Dies ist nur möglich, wenn eine Erhöhung einer Variablen zu einer Erhöhung des Wertes der Funktion führt.

Voraussetzungen für die Anwendung der Simplex-Methode:

1. Die Aufgabe muss eine kanonische Form haben.
2. Die Aufgabe sollte eine explizite Grundlage haben.

Definition: Eine explizit ausgewählte Basis ist ein Vektor der Form:$$ $ inline $ (.. 0100 ..) ^ T, (..010 ..) ^ T, (.. 0010 ..) ^ T ... $ inline $ d.h. Nur eine Koordinate des Vektors ist ungleich Null und gleich 1.

Hinweis: Der Basisvektor hat die Dimension (m * 1), wobei m die Anzahl der Gleichungen im Beschränkungssystem ist.

Zur Vereinfachung der Berechnungen und Visualisierung werden normalerweise Simplex-Tabellen verwendet:

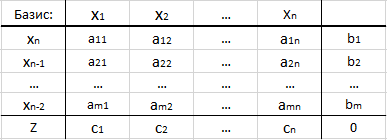
• Die erste Zeile gibt den "Namen" aller Variablen an.
• In der ersten Spalte sind die Nummern der Basisvariablen und in der letzten Zelle der Buchstabe Z (dies ist die Funktionslinie) angegeben.
• In der "Mitte der Tabelle" geben Sie die Koeffizienten der Beschränkungsmatrix - aij an.
• Die letzte Spalte ist der Vektor der rechten Seite der entsprechenden Gleichungen des Beschränkungssystems.
• Die Zelle ganz rechts ist der Wert der Zielfunktion. Bei der ersten Iteration wird 0 angenommen.

Hinweis: Basis sind Variablen, Koeffizienten in der Matrix der Einschränkungen, bei denen Basisvektoren gebildet werden.

Hinweis: Wenn die Einschränkungen im ursprünglichen Problem durch Ungleichungen der Form ≤ dargestellt werden, bilden die eingeführten zusätzlichen Variablen die anfängliche Grundlösung, wenn das Problem auf die kanonische Form reduziert wird.

Hinweis: Die Koeffizienten in der Funktionslinie werden mit dem Vorzeichen „-“ angegeben.

Simplex-Methodenalgorithmus:

1. Wählen Sie eine Variable, die wir in die Basis einführen werden. Dies geschieht nach dem zuvor angegebenen Prinzip: Wir müssen eine Variable wählen, deren Erhöhung zu einer Erhöhung der Funktion führt. Die Auswahl erfolgt nach folgender Regel:

• Wenn die Aufgabe minimal ist, wählen Sie das maximale positive Element in der letzten Zeile aus.
• Wenn die Aufgabe maximal ist, wählen Sie das minimale Negativ aus.

Eine solche Wahl entspricht in der Tat dem oben erwähnten Prinzip: Wenn die Aufgabe minimal ist, nimmt die Funktion umso schneller ab, je größer die Zahl ist, die wir subtrahieren. für das Maximum im Gegenteil - je größer die Zahl hinzugefügt wird, desto schneller wächst die Funktion.

Hinweis: Obwohl wir die minimale negative Zahl im Problem auf das Maximum bringen, zeigt dieser Koeffizient die Wachstumsrichtung der Funktion, da Die Funktionslinie in der Simplex-Tabelle wird mit dem Zeichen „-“ versehen. Eine ähnliche Situation mit Minimierung.

Definition: Eine Spalte einer Simplex-Tabelle, die einem ausgewählten Koeffizienten entspricht, wird als führende Spalte bezeichnet .

2. Wählen Sie eine Variable, die wir in die Basis einführen werden. Dazu müssen Sie bestimmen, welche der Basisvariablen am wahrscheinlichsten verschwindet, wenn die neue Basisvariable wächst. Algebraisch geschieht dies wie folgt:

• Der Vektor der rechten Teile wird durch die Abschlussspalte geteilt
• Wählen Sie unter den erhaltenen Werten das Minimum positiv (negative und Null-Antworten werden nicht berücksichtigt).

Definition: Eine solche Linie wird als führende Linie bezeichnet und entspricht einer Variablen, die aus der Basis abgeleitet werden soll.

Hinweis: Tatsächlich drücken wir die alten Basisvariablen aus jeder Gleichung des Beschränkungssystems durch den Rest der Variablen aus und sehen, in welcher Gleichung die Zunahme der neuen Basisvariablen höchstwahrscheinlich 0 ergibt. Wenn wir in diese Situation geraten, sind wir über einen neuen Scheitelpunkt „gestolpert“. Deshalb werden null und negative Elemente nicht berücksichtigt, weil Das Erhalten eines solchen Ergebnisses bedeutet, dass die Wahl einer solchen neuen Basisvariablen uns von dem Bereich wegführt, über den es keine Lösungen gibt.

3. Wir suchen ein Element, das am Schnittpunkt der führenden Zeile und Spalte steht.

Definition: Ein solches Element wird als führendes Element bezeichnet .

4. Schreiben Sie anstelle der auszuschließenden Variablen in die erste Spalte (mit den Namen der Basisvariablen) den Namen der Variablen, die wir in die Basis eingeben.

5. Als nächstes beginnt der Prozess der Berechnung einer neuen Basislösung. Es tritt nach der Jordan-Gauß-Methode auf .

• Neue Lead Line = Alte Lead Line / Lead
• Neue Zeile = Neue Zeile - Zeilenfaktor in der führenden Spalte * Neue führende Zeile

Hinweis: Eine Konvertierung dieser Art zielt darauf ab, die ausgewählte Variable in die Basis einzuführen, d.h. Darstellung der Leitspalte als Basisvektor.

6. Danach überprüfen wir die Optimalitätsbedingung. Wenn die resultierende Lösung nicht optimal ist, wiederholen Sie den gesamten Vorgang erneut.

§5. Interpretation des Ergebnisses der Simplex-Methode

1. Optimalität

Die Optimalitätsbedingung für die resultierende Lösung:

• Wenn die Aufgabe maximal ist, gibt es keine negativen Koeffizienten in der Funktionszeile (d. H. Bei jeder Änderung der Variablen wächst der Wert der resultierenden Funktion nicht).
• Wenn die Aufgabe minimal ist, gibt es keine positiven Koeffizienten in der Funktionszeile (d. H. Bei jeder Änderung der Variablen nimmt der Wert der resultierenden Funktion nicht ab).

2. Unbegrenzte Funktionalität

Es ist jedoch anzumerken, dass eine bestimmte Funktion in einem bestimmten Bereich möglicherweise kein Maximum / Minimum erreicht. Das algebraische Attribut hierfür kann wie folgt formuliert werden:

Bei der Auswahl einer führenden Zeile (Variable, die ausgeschlossen werden soll) enthält das Ergebnis der termweisen Division des Vektors der rechten Seite durch die führende Spalte nur Null- und negative Werte.

Tatsächlich bedeutet dies, dass wir unabhängig von dem Wachstum, für das wir eine neue Basisvariable festlegen, niemals einen neuen Scheitelpunkt finden werden. Unsere Funktion ist also nicht auf die möglichen Lösungen beschränkt.

3. Alternative Lösungen

Bei der Suche nach der optimalen Lösung ist eine andere Option möglich - es gibt alternative Lösungen (ein weiterer Eckpunkt, der den gleichen Wert der Funktion ergibt).

Algebraisches Zeichen für die Existenz einer Alternative:

Nach Erreichen der optimalen Lösung gibt es in der Funktionszeile keine Koeffizienten für freie Variablen.

Dies bedeutet, dass sich mit dem Wachstum der entsprechenden Variablen mit einem Koeffizienten von Null der Wert der Funktion nicht ändert und eine neue Grundlösung auch das Optimum der Funktion ergibt.

Nachwort

Dieser Artikel zielt auf ein tieferes Verständnis des theoretischen Teils ab. In den Kommentaren und Erklärungen hier finden Sie Antworten auf Fragen, die normalerweise beim Studium dieser Methode weggelassen und a priori genommen werden. Man muss jedoch verstehen, dass viele Methoden der numerischen Optimierung auf der Simplex-Methode basieren (zum Beispiel die Gomori-Methode , die M-Methode ), und ohne ein grundlegendes Verständnis ist es unwahrscheinlich, dass bei der weiteren Untersuchung und Anwendung aller Algorithmen dieser Klasse große Fortschritte erzielt werden können.

Wenig später werde ich einen Artikel über die praktische Implementierung der Simplex-Methode sowie mehrere Artikel über die Methode der künstlichen Variablen (M-Methode), die Gomori-Methode und die Verzweigungs- und Grenzmethode schreiben.

Vielen Dank für Ihre Aufmerksamkeit!

PS

Wenn Sie bereits von der Implementierung der Simplex-Methode gequält werden, empfehle ich Ihnen, das Buch von A. Taha zu lesen. Einführung in das Studium der Operationen - dort ist alles gut analysiert, sowohl in der Theorie als auch in Beispielen; Schauen Sie sich auch Beispiele zur Lösung von matburo.ru-Problemen an - dies hilft bei der Implementierung in Code.