Alan Turing Book und Mysterious Note - Wissenschaftsdetektiv

Originalübersetzung in meinem Blog

Wie kam dieses Buch zu mir?

Im Mai 2017 erhielt ich eine E-Mail von meinem alten Gymnasiallehrer namens George Rutter, in der er schrieb: „ Ich habe eine Kopie des großen deutschen Dirac-Buches (Die Prinzipien der Quantenmechanik), das Alan Turing und später gehörte Als ich Ihr Buch Idea Makers las, schien es mir selbstverständlich, dass Sie die Person sind, die es braucht . " Er erklärte mir, dass er ein Buch von einem anderen (zu diesem Zeitpunkt verstorbenen) Schullehrer Norman Rutledge erhalten hatte , von dem ich wusste, dass er ein Freund von Alan Turing war. George schloss seinen Brief mit dem Satz: " Wenn Sie dieses Buch brauchen, könnte ich es Ihnen geben, wenn Sie das nächste Mal nach England kommen ."

Nach ein paar Jahren im März 2019 kam ich wirklich in England an, danach stimmte ich George zu, mich zum Frühstück in einem kleinen Hotel in Oxford zu treffen. Wir aßen, plauderten und warteten darauf, dass sich das Essen beruhigte. Dann kam der richtige Moment, um das Buch zu besprechen. George steckte seine Hand in seine Aktentasche und holte einen eher bescheiden gestalteten, typischen akademischen Band aus der Mitte des 20. Jahrhunderts heraus.



Ich öffnete den Umschlag und fragte mich, ob er auf der Rückseite der Inschrift stehen könnte: " Alan Turings Eigentum" oder so ähnlich. Dies war leider nicht der Fall. Dennoch wurde ihm eine hinreichend aussagekräftige Notiz auf vier Blättern von Norman Rutledge bis George Rutter aus dem Jahr 2002 beigefügt.

Ich kannte Norman Rutledge, als ich Anfang der 1970er Jahre noch Schüler in Eton war . Er war ein Mathematiklehrer mit dem Spitznamen The Nutty Norman. Er war in jeder Hinsicht ein angenehmer Lehrer und erzählte endlose Geschichten über Mathematik und alle möglichen anderen interessanten Dinge. Er war dafür verantwortlich, dass die Schule einen Computer erhielt (programmiert mit einem Lochstreifen in der Breite eines Schreibtisches) - dies war der allererste Computer, den ich jemals benutzt hatte .

In jenen Tagen wusste ich nichts über Normans Vergangenheit (denken Sie daran, dass dies lange vor dem Aufkommen des Internets war). Ich wusste nur, dass er "Dr. Rutledge" war. Er erzählte oft Geschichten von Leuten aus Cambridge, aber in seinen Geschichten erwähnte er Alan Turing nie. Natürlich war Turing damals nicht berühmt genug (obwohl ich, wie sich herausstellte, bereits von jemandem von ihm gehört habe, der ihn im Bletchley Park kannte (dem Herrenhaus, in dem sich das Verschlüsselungszentrum während des Zweiten Weltkriegs befand)).

Alan Turing war erst 1981 berühmt, als ich anfing, einfache Programme zu studieren , allerdings damals im Zusammenhang mit zellularen Automaten und nicht mit Turing-Maschinen .

Plötzlich, als ich eines Tages einen Katalog von Karten in der Bibliothek des California Institute of Technology ansah, stieß ich auf das Buch Alan M. Turing , geschrieben von seiner Mutter Sarah Turing. Das Buch enthielt viele Informationen, darunter Turings unveröffentlichte wissenschaftliche Arbeiten zur Biologie. Ich habe jedoch nichts über seine Beziehung zu Norman Rutledge erfahren, da das Buch nichts über ihn erwähnte (obwohl Sarah Turing, wie ich herausfand, mit Norman über dieses Buch korrespondierte und Norman am Ende sogar eine Rezension darüber schrieb).



Zehn Jahre später besuchte ich mit äußerster Neugier für Turing und seine (damals unveröffentlichte) biologische Arbeit das Turing-Archiv am King's College in Cambridge . Bald, nachdem ich mich mit dem vertraut gemacht hatte, was sie von Turings Arbeit hatten, und nachdem ich einige Zeit damit verbracht hatte, dachte ich, dass ich ihn gleichzeitig bitten könnte, auch seine persönliche Korrespondenz zu sehen. Beim Durchsehen fand ich mehrere Briefe von Alan Turing an Norman Rutledge.

Zu dieser Zeit wurde die Biografie von Andrew Hodges veröffentlicht, die so viel dazu beitrug, dass Turing endlich berühmt wurde. Sie bestätigte, dass Alan Turing und Norman Rutledge wirklich befreundet waren und dass Turing ein wissenschaftlicher Berater von Norman war. Ich wollte Rutledge nach Turing fragen, aber zu diesem Zeitpunkt war Norman bereits im Ruhestand und führte ein abgeschiedenes Leben. Als ich jedoch die Arbeit an dem Buch A New Kind of Science im Jahr 2002 (nach meinem zehnjährigen Exerzitienaufenthalt) abgeschlossen hatte, machte ich es mir zu schaffen und schickte ihm eine Kopie des Buches mit der Überschrift „To My Last Math Teacher“. Dann haben wir ein bisschen korrespondiert , und 2005 bin ich wieder nach England gekommen und habe mich mit Norman auf eine Tasse Tee in einem Luxushotel im Zentrum von London verabredet.

Wir hatten ein nettes Gespräch über viele Dinge, einschließlich Alan Turing. Norman begann unser Gespräch mit der Geschichte, dass er Turing vor 50 Jahren größtenteils oberflächlich kannte. Trotzdem hatte er persönlich etwas über ihn zu erzählen: " Er war nicht kontaktfreudig ." " Er hat viel gekichert ." " Er konnte nicht wirklich mit den Nicht-Mathematikern sprechen ." " Er hatte immer Angst, seine Mutter zu verärgern ." " Er ist tagsüber gegangen und ist einen Marathon gelaufen ." " Er war nicht zu ehrgeizig ." Dann kehrte das Gespräch zu Normans Identität zurück. Er sagte, dass er trotz der Tatsache, dass er bereits seit 16 Jahren im Ruhestand sei, immer noch Artikel für die Mathematische Zeitung schreibe, um in seinen Worten „ alle seine wissenschaftlichen Arbeiten zu vervollständigen, bevor er in eine andere Welt zieht “. , wo, wie er mit einem kaum wahrnehmbaren Lächeln hinzufügte, " alle mathematischen Wahrheiten sicherlich enthüllt werden ". Als die Teeparty vorbei war, zog Norman seine Lederjacke an und ging zu seinem Moped. Er ignorierte die Explosionen, die den Verkehr in London an diesem Tag störten .

Dies war das letzte Mal, dass ich Norman sah, er starb 2013.

Sechs Jahre später saß ich mit George Rutter beim Frühstück. Bei mir war eine Notiz von Rutledge, die er 2002 in seiner charakteristischen Handschrift schrieb:



Zuerst las ich die Notiz fließend. Sie war wie immer ausdrucksstark:

Ich erhielt ein Buch von Alan Turing von seinem Freund und Testamentsvollstrecker Robin Gandy (am King's College war es normal, Bücher aus der Sammlung verstorbener Genossen herauszugeben, und ich wählte die Gedichtsammlung von A. E. Housman aus Ivor Ramseys Büchern als geeignetes Geschenk (er war der Dekan und sprang aus der Kapelle [1956]) ...

Später in einer kurzen Notiz schreibt er:

Sie fragen, wohin dieses Buch letztendlich hätte führen sollen - meiner Meinung nach sollte es an jemanden gehen, der alles schätzt, was mit Turings Arbeit zu tun hat, also hängt sein Schicksal von Ihnen ab.

Stephen Wolfram hat mir sein beeindruckendes Buch geschickt, aber ich bin nicht tief genug hineingetaucht ...

Abschließend gratulierte er George Rutter zu seinem Mut, nach seiner Pensionierung (wie sich vorübergehend herausstellte) nach Australien zu ziehen, und sagte, er selbst würde " als Beispiel für eine billige und lotusähnliche Existenz nach Sri Lanka ziehen ". fügte jedoch hinzu, dass "die Ereignisse, die sich dort abspielen, darauf hindeuten, dass er dies nicht hätte tun dürfen " (offenbar in Bezug auf den Bürgerkrieg in Sri Lanka).

Was verbirgt sich also in den Gedärmen des Buches?

Also, was habe ich mit einer Kopie eines deutschsprachigen Buches von Paul Dirac gemacht, das einst Alan Turing gehörte? Ich lese kein Deutsch, aber ich hatte ein Exemplar desselben Buches in Englisch (das ist die Sprache des Originals) der Ausgabe der 1970er Jahre. Trotzdem schien es mir einmal beim Frühstück richtig, dass ich das Buch Seite für Seite sorgfältig durchsehen sollte. Am Ende ist dies eine gängige Praxis im Umgang mit antiken Büchern.

Es sollte angemerkt werden, dass ich von der Eleganz von Diracs Präsentation beeindruckt war. Das Buch wurde 1931 veröffentlicht, aber sein reiner Formalismus (und trotz der Sprachbarriere konnte ich die in dem Buch beschriebene Mathematik lesen) ist fast so, als wäre es heute geschrieben worden. (Ich möchte mich hier nicht zu sehr auf Dirac konzentrieren, aber mein Freund Richard Feynman sagte mir, dass Diracs Darstellung zumindest seiner Meinung nach einsilbig ist. Norman Rutledge sagte mir, dass er mit Diracs Adoptivsohn befreundet war, der in Cambridge Theoretiker wurde Norman war ziemlich oft in Diracs Haus und sagte, der "große Mann" sei manchmal persönlich in den Hintergrund getreten, während der Vordergrund immer viele mathematische Rätsel hatte. Leider habe ich selbst Paul Dirac nie getroffen, obwohl Mir wurde gesagt, dass nach t wow, als er Cambridge endgültig verließ und nach Florida ging, verlor er den größten Teil seiner früheren Steifheit und wurde eine ziemlich gesellige Person.

Aber zurück zum Buch Dirac, das Turing gehörte. Auf Seite 9 bemerkte ich Unterstreichungen und kleine Randnotizen, die mit einfachem Bleistift geschrieben waren. Ich blätterte weiter. Nach mehreren Kapiteln verschwanden die Notizen. Aber dann fand ich plötzlich eine in Seite 127 eingebettete Notiz mit folgendem Inhalt:



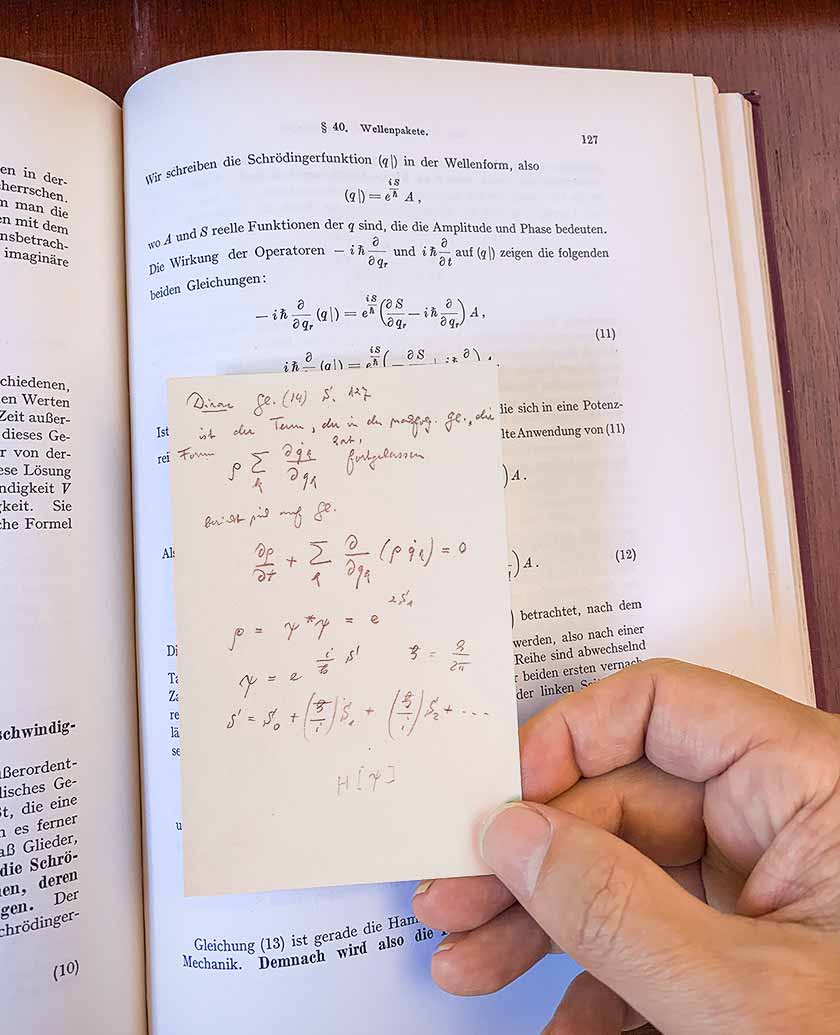
Es wurde in deutscher Standardhandschrift in deutscher Sprache verfasst. Und es sieht so aus, als könnte es irgendwie mit der Lagrange-Mechanik zusammenhängen . Ich dachte, dass wahrscheinlich jemand dieses Buch vor Turing besaß, und dies muss eine Notiz sein, die von dieser Person geschrieben wurde.

Ich blätterte weiter im Buch. Keine Notizen. Und ich dachte, ich könnte nichts mehr finden. Aber dann fand ich auf Seite 231 das Firmenlesezeichen - mit gedrucktem Text:



Werde ich irgendwann noch etwas finden? Ich blätterte weiter im Buch. Dann fand ich am Ende des Buches auf Seite 259 im Abschnitt über die relativistische Theorie der Elektronen Folgendes:



Ich habe dieses Blatt Papier entfaltet:



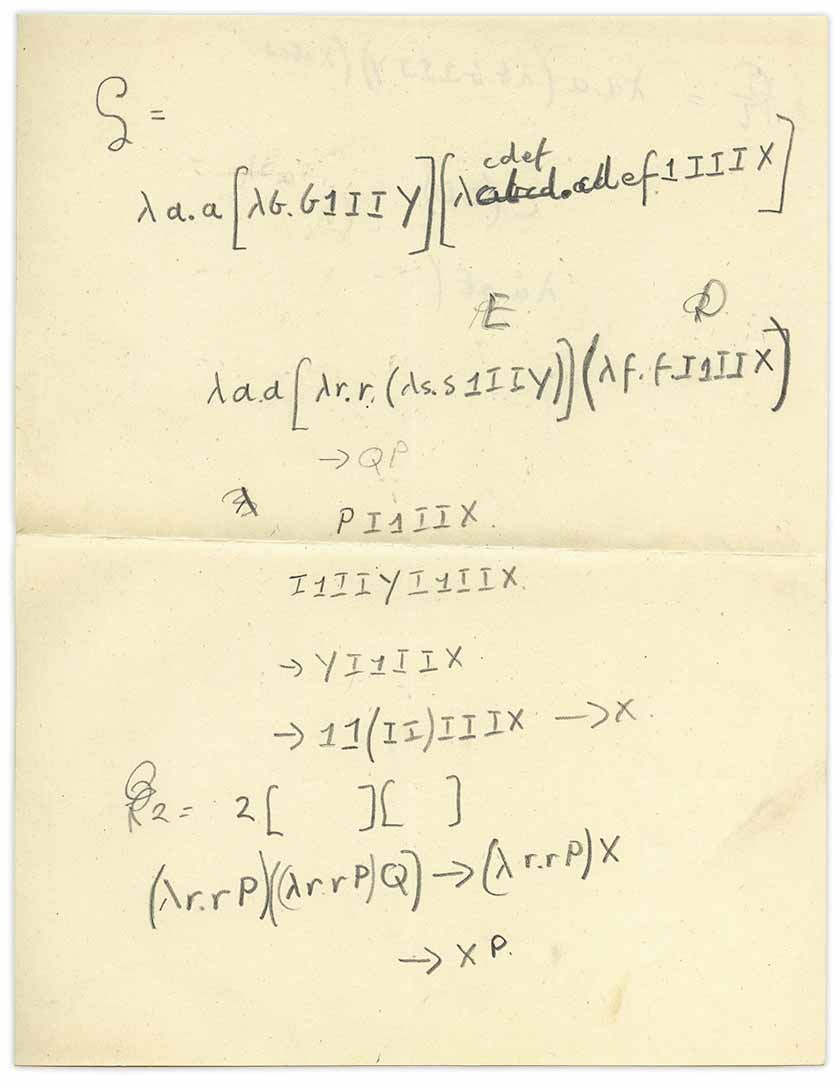
Mir wurde sofort klar, dass dies ein Lambda-Kalkül mit einer Beimischung von Kombinatoren war , aber wie erschien dieses Blatt hier? Erinnern Sie sich daran, dass dieses Buch ein Buch über Quantenmechanik ist, aber das beigefügte Blatt befasst sich mit mathematischer Logik oder der heutigen Berechnungstheorie. Dies ist typisch für Turings Schriften. Ich fragte mich, ob Turing diese Notiz persönlich schrieb.

Selbst während des Frühstücks suchte ich im Internet nach Turings Handschriftmustern, fand jedoch keine Beispiele in Form von Berechnungen, sodass ich keine Rückschlüsse auf die genaue Identität der Handschrift ziehen konnte. Und bald musste ich gehen. Ich packte das Buch sorgfältig ein, um das Geheimnis zu enthüllen, was die Seite war und wer sie geschrieben hatte, und nahm sie mit.

Über das Buch

Lassen Sie uns zunächst das Buch selbst diskutieren. Die Prinzipien der Quantenmechanik von Paul Dirac wurden 1930 in englischer Sprache veröffentlicht und bald ins Deutsche übersetzt. (Diracs Vorwort ist vom 29. Mai 1930 datiert; es gehört dem Übersetzer Werner Bloch am 15. August 1930.) Das Buch wurde zu einem Meilenstein in der Entwicklung der Quantenmechanik, indem es systematisch einen klaren Formalismus für die Durchführung von Berechnungen etablierte und unter anderem Diracs Vorhersage über das Positron erklärte 1932 eröffnet.

Warum hatte Alan Turing ein Buch auf Deutsch, nicht auf Englisch? Ich weiß das nicht genau, aber damals war Deutsch die führende Wissenschaftssprache, und wir wissen, dass Alan Turing es lesen konnte. (Immerhin im Titel seiner berühmten Turing- Maschinenarbeit “ Über berechenbare Zahlen mit einem Anhang zum Entscheidungsproblem war ein sehr langes deutsches Wort - und im Hauptteil des Artikels arbeitet er mit eher obskuren gotischen Zeichen in Form von „deutschen Buchstaben“, die er anstelle von beispielsweise griechischen Zeichen verwendete).

Alan Turing hat das Buch selbst gekauft oder ihm übergeben? Ich weiß nicht. Auf der Innenseite des Umschlags von Turings Buch befindet sich eine Bleistiftnotation „20 / -“, bei der es sich um die Standardnotation „20 Schilling“ handelt, ähnlich wie bei £ 1. Auf der rechten Seite steht ein gelöschter „26.9.30“, der angeblich den 26. September 1930 bedeutet - vielleicht das Datum, an dem das Buch zum ersten Mal gekauft wurde. Dann ist in der äußersten rechten Ecke die gelöschte Zahl "20". Vielleicht ist das wieder der Preis. (Könnte dies der Preis in der Reichsmark sein , wenn wir davon ausgehen, dass das Buch in Deutschland verkauft wurde? Damals war 1 Reichsmark ungefähr 1 Schilling wert, der deutsche Preis würde wahrscheinlich wie zum Beispiel "20 RM" geschrieben werden.) Zum Schluss Die Innenseite der Rückseite ist "c 5 / -" - vielleicht ist es (mit einem großen Rabatt) der Preis für ein gebrauchtes Buch.

Schauen wir uns die wichtigsten Daten von Alan Turings Leben an. Alan Turing wurde am 23. Juni 1912 geboren (zufällig genau 76 Jahre vor Mathematica 1.0 ). Im Herbst 1931 trat er in das King's College in Cambridge ein. Er erhielt seinen Bachelor-Abschluss nach dreijährigem Standardstudium im Jahr 1934.

In den 1920er und frühen 1930er Jahren war die Quantenmechanik ein heißes Thema, und Alan Turing war sicherlich daran interessiert. Aus seinen Archiven wissen wir, dass er 1932, sobald das Buch veröffentlicht wurde, die " Mathematischen Grundlagen der Quantenmechanik " von John von Neumann erhielt. Wir wissen auch, dass Turing 1935 vom Cambridge-Physiker Ralph Fowler eine Aufgabe zum Thema Quantenmechanik erhielt. (Fowler schlug vor, die Dielektrizitätskonstante von Wasser zu berechnen, was eigentlich eine sehr schwierige Aufgabe ist und eine vollständige Analyse mit der Theorie des wechselwirkenden Quantenfeldes erfordert, die immer noch nicht vollständig gelöst ist.)

Und doch, wann und wie hat Turing Diracs Buch bekommen? Da das Buch einen gebrochenen Preis hat, hat Turing es angeblich bereits gebraucht gekauft. Wer war der erste Besitzer des Buches? Die Anmerkungen im Buch scheinen sich hauptsächlich auf die logische Struktur zu beziehen, es wird angemerkt, dass eine logische Beziehung als Axiom betrachtet werden sollte. Was ist dann mit dem Hinweis auf Seite 127?

Nun, das mag ein Zufall sein, aber nur auf Seite 127 - Dirac spricht über das Quantenprinzip der geringsten Aktion und legt den Grundstein für ein Integral entlang des Feynman-Pfades - der die Grundlage allen modernen Quantenformalismus bildet. Was enthält die Notiz? Es enthält eine Erweiterung von Gleichung 14, die eine Gleichung für die zeitliche Entwicklung der Quantenamplitude ist. Der Autor der Notiz ersetzte Dirac A für die Amplitude durch ρ, was möglicherweise die frühere deutsche Aufzeichnung (Analogie der Flüssigkeitsdichte) widerspiegelt. Dann versucht der Autor, die Wirkung in Potenzen von ℏ zu erweitern (die Planck-Konstante geteilt durch 2π, die manchmal als Dirac-Konstante bezeichnet wird ).

Aber es scheint, dass aus dem, was auf der Seite enthalten ist, wenig Nützliches gelernt werden kann. Wenn Sie die Seite im Licht halten, enthält sie eine kleine Überraschung - ein Wasserzeichen mit der Aufschrift "Z f. Physik. Chem. B ”:



Dies ist eine Kurzfassung der Zeitschrift für physikalische Chemie, Abteilung B , die seit 1928 herausgegeben wird. Vielleicht wurde die Notiz vom Journal-Editor geschrieben? Hier ist der Titel der Zeitschrift für 1933. Praktischerweise werden die Redakteure mit ihrem Standort aufgelistet, und einer von ihnen sticht heraus: „Born · Cambridge“.



Dies ist Max Bourne , der Autor der Bourne-Regel und vieles mehr in der Theorie der Quantenmechanik (sowie der Großvater der Sängerin Olivia Newton-John ). Also, diese Notiz könnte von Max Born geschrieben worden sein? Dies ist aber leider nicht der Fall, da die Handschrift nicht übereinstimmt.

Was ist mit den Lesezeichen auf Seite 231? Hier ist es von zwei Seiten:



Das Lesezeichen ist seltsam und hübsch hübsch. Aber wann wurde es gemacht? In Cambridge gibt es eine Heffers-Buchhandlung , die inzwischen zu Blackwell gehört. Wie aus dem Lesezeichen hervorgeht, befand sich Heffers über 70 Jahre (bis 1970) unter der Adresse 3 und 4 von Petty Cury .

Diese Registerkarte enthält einen wichtigen Schlüssel - dies ist die Telefonnummer „Tel. 862. " Es stellte sich heraus, dass 1939 der größte Teil von Cambridge (einschließlich Heffers) auf vierstellige Nummern umstellte und natürlich bis 1940 Lesezeichen mit "modernen" Telefonnummern gedruckt wurden. (Die englischen Telefonnummern wurden allmählich länger. Als ich in den 1960er Jahren in England aufwuchs, waren unsere Telefonnummern Oxford 56186 und Kidmore End 2378. Zum Teil erinnere ich mich an diese Nummern, weil es seltsamerweise jetzt ist es sah nicht so aus, ich habe meine Nummer immer angerufen, wenn ich einen eingehenden Anruf angenommen habe).

Das Lesezeichen in dieser Form wurde bis 1939 gedruckt. Aber wie lange noch? Spätestens seit 1912 finden Sie im Internet einige Scans von alten Heffers-Anzeigen (zusammen mit „Wir bitten Sie, Ihre Anforderungen zu erfüllen ...“), in denen „Telefon 862“ und „(2 Zeilen)“ hinzugefügt sind. Es gibt auch einige Lesezeichen mit einem ähnlichen Design, die seit 1904 in Büchern zu finden sind (obwohl nicht klar ist, ob sie für diese Bücher original waren (dh gleichzeitig gedruckt wurden). Für die Zwecke unserer Untersuchung können wir daraus schließen Dieses Buch stammte zwischen 1930 und 1939 aus dem Heffers-Laden (der übrigens der Hauptbuchladen in Cambridge war).

Seite mit Lambda-Kalkül

Jetzt wissen wir also etwas darüber, wann das Buch gekauft wurde. Aber was ist mit der „Lambda-Kalkülseite“? Wann wurde das geschrieben? , - . , , 1932 1935 . ( , λ).

-. 1935 «» , . ( Comptes rendus ), ; , , , , .

1936 , - , . , 1934 , , , 1922 .
, - , ( - ). ( ) , , . 1936 ( ) « …» .

: 1936 1938 ( 1937 ) , , . , -, — , - , — , , .

1938 , , -, , . 1945 , . 1947–8 , , .

1951 . ( , , , , - , ). , 1954 , : « » ( : « , »). , , 7 1954 , . ( , , .)

, -. , :



, , , . ? , , , Spalding&Hodge, Papermakers, « », - , -, . , , , Excelsior, , 1890- 1954 .

Was sagt diese Seite?

Schauen wir uns also genauer an, was sich auf beiden Seiten des Blattes befindet. Beginnen wir mit Lambdas.

Hier ist eine Möglichkeit, "reine" oder "anonyme" Funktionen zu definieren. Sie sind das Grundkonzept in der mathematischen Logik und jetzt in der funktionalen Programmierung. Diese Funktionen sind in der Wolfram-Sprache weit verbreitet , und ihre Funktionsweise ist recht einfach zu erklären. Zum Beispiel schreibt jemand f [ x ], um die auf das Argument x angewendete Funktion f zu bezeichnen. Und es gibt viele benannte f- Funktionen wie Abs oder Sin oder Blur . Aber was ist, wenn jemand möchte, dass f [ x ] 2x +1 ist ? Es gibt keinen unmittelbaren Namen für diese Funktion. Aber gibt es eine andere Form der Zuordnung, f [ x ]?

Die Antwort lautet ja: anstelle von f schreiben wir Function[a,2a+1] . Und in der Wolfram- Function [a,2a+1][x] wendet Function [a,2a+1][x] Funktionen auf das Argument x an, was zu 2x+1 führt. Function[a,2a+1] ist eine "reine" oder "anonyme" Funktion, bei der es sich um eine reine Operation handelt, bei der mit 2 multipliziert und 1 addiert wird.

So ist λ in der Lambda-Rechnung ein genaues Analogon der Funktion in der Wolfram-Sprache - und daher entspricht beispielsweise λ a (2 a + 1) der Function[a, 2a + 1] . (Es ist erwähnenswert, dass die Funktion, z. B. Function[b,2b+1] äquivalent ist. Die „verwandten Variablen“ a oder b sind nur Stellen zum Ersetzen des Arguments der Funktion - und in der Wolfram-Sprache können sie vermieden werden, indem alternative Optionen zum Definieren einer reinen Funktion verwendet werden (2# +1)& ).

In der traditionellen Mathematik werden Funktionen normalerweise als Objekte betrachtet, die Eingabedaten (z. B. Ganzzahlen) und Ausgabedaten (z. B. auch Ganzzahlen) anzeigen. Aber was ist dieses Funktionsobjekt (oder λ)? Im Wesentlichen ist dies ein struktureller Operator, der Ausdrücke aufnimmt und sie in Funktionen umwandelt. Dies mag in Bezug auf die traditionelle Mathematik und die mathematische Form des Schreibens etwas seltsam erscheinen, aber wenn jemand beliebige Zeichen manipulieren muss, ist dies viel natürlicher, auch wenn es zunächst ein bisschen abstrakt erscheint. (Es sollte beachtet werden, dass Benutzer, die die Wolfram-Sprache lernen, immer sagen können, dass sie eine bestimmte Schwelle des abstrakten Denkens überschritten haben, wenn sie eine Vorstellung von der Funktion bekommen. )

Lambdas sind nur ein Teil dessen, was auf der Seite steht. Es gibt ein anderes, noch abstrakteres Konzept - dies sind Kombinatoren . Betrachten Sie die eher dunkle PI1IIx Linie? Was bedeutet das Tatsächlich ist dies eine Folge von Kombinatoren oder eine abstrakte Zusammensetzung symbolischer Funktionen.

Die übliche mathematische Überlagerung von Funktionen in der Wolfram-Sprache kann in der folgenden Form geschrieben werden: f[g[x]] - was bedeutet, "wende f auf das Ergebnis der Anwendung von g auf x an ". Aber werden dafür wirklich Klammern benötigt? In Wolfram ist f@g@ x eine alternative Form der Notation. In diesem Beitrag stützen wir uns auf die Wolfram-Sprachdefinition: Der @ -Operator ist der rechten Seite zugeordnet, daher entspricht f@g@x f@(g@x) .

Aber was bedeutet der Eintrag (f@g)@x ? Dies entspricht f[g][x] . Und wenn f und g gewöhnliche Funktionen in der Mathematik wären, wäre das sinnlos, aber wenn f eine Funktion höherer Ordnung ist , dann kann f[g] selbst eine Funktion sein, die sehr gut auf x angewendet werden kann.

Beachten Sie, dass hier noch einige Komplexität besteht. In f[] - f ist eine Funktion eines Arguments. Und f[] entspricht dem Schreiben von Function[a, f[a]][x] . Aber was ist mit der Funktion zweier Argumente, sagen wir f[x,y] ? Dies kann als Function[{a,b},f[a, b]][x, y] . Aber was ist mit Function[{a},f[a,b]] ? Was ist das? Es gibt eine "freie Variable" b , die einfach an die Funktion übergeben wird. Function[{b},Function[{a},f[a,b]]] bindet diese Variable und dann Function[{b},Function[{a},f [a, b]]][y][x] gibt wieder f[x,y] . (Das Setzen der Funktion auf ein Argument wird zu Ehren des Wissenschaftlers Haskell Curry als "Curry" bezeichnet.)

Wenn freie Variablen existieren, das heißt, es gibt viele verschiedene Schwierigkeiten, wie Funktionen definiert werden können, aber wenn wir uns auf Funktions- oder λ-Objekte beschränken, die keine freien Variablen haben, können sie grundsätzlich frei gesetzt werden. Solche Objekte werden Kombinatoren genannt.

Kombinatoren haben eine lange Geschichte. Es ist bekannt, dass sie erstmals 1920 von David Gilberts Schüler Moses Schoenfinkel vorgeschlagen wurden .

Damals wurde erst vor kurzem festgestellt, dass es nicht erforderlich ist, die Ausdrücke And , Or und Not zu verwenden, um Ausdrücke in der Standardsatzlogik darzustellen: Es genügte, den einzigen Operator zu verwenden, den wir jetzt Nand nennen (weil zum Beispiel, wenn wir Nand als schreiben) ·, Dann Or[a,b] hat die Form (a · a) · (b · b) ). Schönfinkel wollte die gleiche minimale Darstellung der Prädikatenlogik oder im Wesentlichen der Logik einschließlich der Funktionen finden.

Er kam mit zwei "Kombinatoren" S und K. In der Wolfram-Sprache ist dies geschrieben als
K [x _] [y_] → x und S [x _] [y _] [z_] → x [z] [y [z]].

Es ist bemerkenswert, dass es möglich war, diese beiden Kombinatoren zu verwenden, um irgendwelche Berechnungen durchzuführen. So zum Beispiel

S [K [S]] [S [K [S [K [S]]] [S [K [K]]]

kann als Funktion zum Hinzufügen von zwei Ganzzahlen verwendet werden.

All dies, um es milde auszudrücken, sind eher abstrakte Objekte, aber jetzt, da wir verstehen, was Turing-Maschinen und Lambda-Kalkül sind, können wir sehen, dass die Schönfinkel-Kombinatoren das Konzept des Universal Computing tatsächlich vorweggenommen haben. (Und noch bemerkenswerter ist, dass die Definitionen von S und K von 1920 minimal einfach sind und der sehr einfachen Universal-Turing-Maschine ähneln, die ich in den 1990er Jahren vorgeschlagen habe und deren Universalität 2007 bewiesen wurde ).

Aber zurück zu unserer Broschüre und Zeile PI1IIx . Die hier aufgezeichneten Zeichen sind Kombinatoren und alle zur Definition einer Funktion vorgesehen. Hier lautet die Definition, dass die Überlagerung von Funktionen linksassoziativ sein sollte, sodass fgx nicht als f @ g @ x oder f @ (g @ x) oder f [g [x]] interpretiert werden sollte, sondern als (f @ g ) @x oder f [g] [x]. Wir werden diesen Eintrag in ein Format übersetzen, das für die Verwendung durch Wolfram Language geeignet ist : PI1IIx hat die Form p [i] [eins] [i] [i] [x] .

Warum so etwas schreiben? Um dies zu erklären, müssen wir das Konzept der Kirchennummern (benannt nach der Alonzo-Kirche) diskutieren. Nehmen wir an, wir arbeiten nur mit Symbolen und mit Lambdas oder Kombinatoren. Gibt es eine Möglichkeit, sie zum Angeben von Ganzzahlen zu verwenden?

Wie wäre es einfach zu sagen, dass die Zahl n der Function[x, Nest[f,x,n]] ? Oder mit anderen Worten, dass (in kürzerer Notation):

1 ist f[#]&
2 ist f[f[#]]&
3 ist f[f[f[#]]]& und so weiter.

All dies mag etwas dunkler erscheinen, aber der Grund, warum es interessant ist, ist, dass wir damit alles vollständig symbolisch und abstrakt machen können, ohne explizit über so etwas wie Ganzzahlen sprechen zu müssen.

Stellen Sie sich bei dieser Methode zum Angeben von Zahlen beispielsweise vor, Sie würden zwei Zahlen hinzufügen: 3 kann als f[f[f[#]]]& und 2 als f[f[#]]& . Sie können sie einfach hinzufügen, indem Sie eine davon auf die andere anwenden:



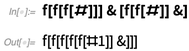
Aber wie ist f ? Es könnte alles sein! In gewisser Weise "gehe zum Lambda" bis zum Ende und stelle Zahlen mit Funktionen dar, die f als Argument verwenden. Mit anderen Worten, stellen Sie sich 3 zum Beispiel als Function[f,f[f[f[#]]] &] oder Function[f,Function[x,f[f[f[x]]]] . (Wann und wie Sie Variablen benennen müssen, ist ein Haken in der Lambda-Rechnung).

Betrachten Sie ein Fragment von Turings 1937er Arbeit Computability and λ-Diffusibility , in der Objekte genau so aufgebaut werden, wie wir es gerade besprochen haben:



Hier kann die Aufnahme etwas verwirrend sein. Turings x ist unser f , und sein x ' (der Komponist hat einen Fehler gemacht, indem er ein Leerzeichen eingefügt hat) ist unser x . Aber hier wird genau der gleiche Ansatz verwendet.

Schauen wir uns also die Linie unmittelbar nach der Falte vor dem Blatt an. Das ist I1IIYI1IIx . Entsprechend der Form der Wolfram-Sprache wird dies i[one][i][i][y][i][one][i][i][x] . Aber hier ist i eine identische Funktion, daher gibt i[one] nur eine zurück . In der Zwischenzeit ist eins die numerische Darstellung von Church für 1 oder Function[f,f[#]&] . Aber mit dieser Definition wird one[] a[#]& und one[a][b] wird a[b] . (Übrigens ist i[][b] oder Identity[][b] auch a [b] ).

Es wird viel klarer, wenn wir die Ersetzungsregeln für i und eins aufschreiben, anstatt direkt den Lambda-Kalkül zu verwenden. Das Ergebnis wird dasselbe sein. Wenden Sie diese Regeln explizit an, erhalten wir:



Und das ist genau das gleiche wie in der ersten abgekürzten Aufzeichnung:



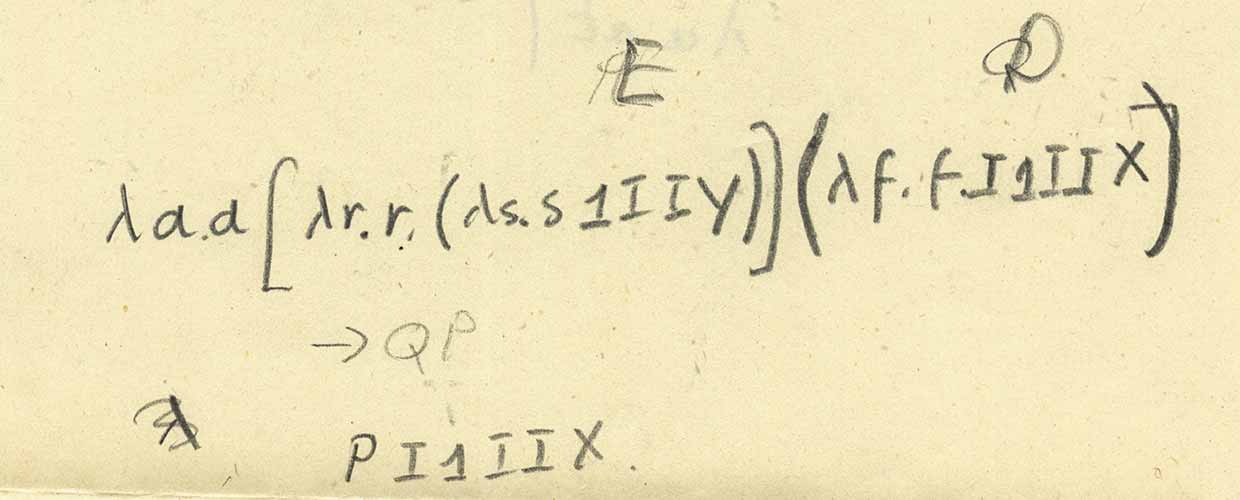
Schauen wir uns jetzt noch einmal das Blatt oben an:



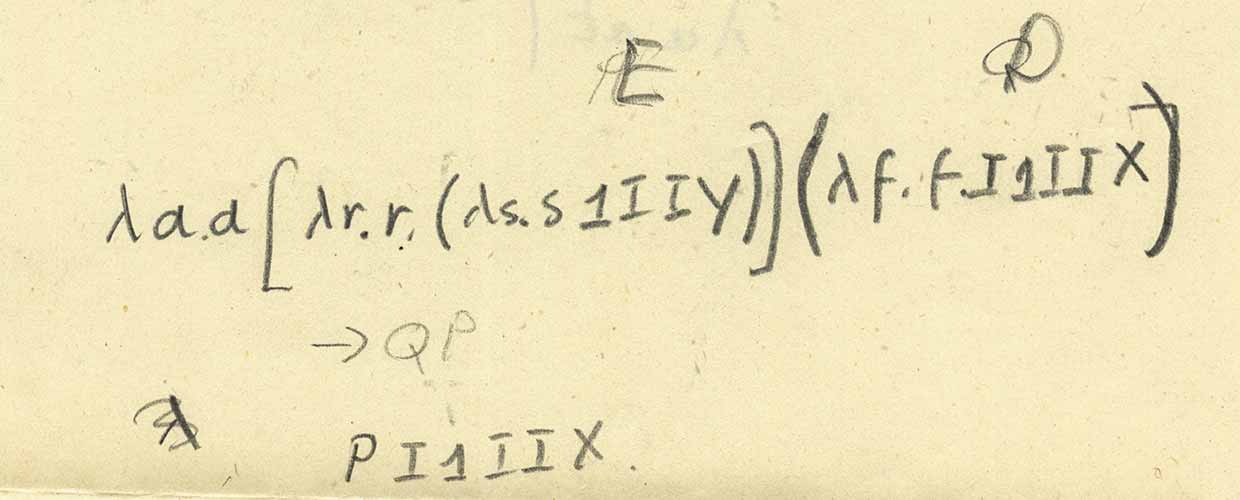
Hier gibt es ziemlich verwirrende und unverständliche Objekte "E" und "D", aber mit ihnen meinen wir "P" und "Q", so dass wir den Ausdruck ausschreiben und berechnen können (beachten Sie dies hier - nach einiger Verwechslung mit dem allerletzten Symbol - "mysteriöser Wissenschaftler" stellt [...] und (...) die Anwendungsfunktionen dar):



Das ist also die erste Abkürzung. Um mehr zu sehen, ersetzen wir die Definitionen für Q:



Wir erhalten genau die folgende Abkürzung. Was passiert, wenn wir P durch die Ausdrücke ersetzen?



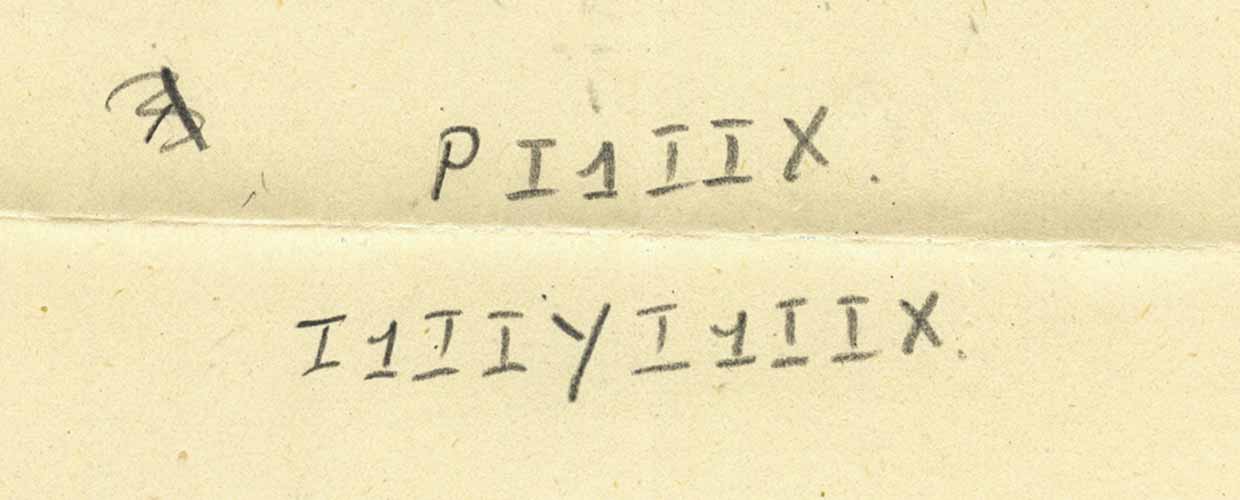
Hier ist das Ergebnis:



Und jetzt, wenn wir die Tatsache verwenden, dass i eine Funktion ist, die das Argument selbst ausgibt, erhalten wir:



Ups! Dies ist jedoch nicht die nächste aufgezeichnete Zeile. Gibt es hier einen Fehler? Unverständlich. Denn am Ende gibt es im Gegensatz zu den meisten anderen Fällen keinen Pfeil, der anzeigt, dass die nächste Zeile aus der vorherigen folgt.

Hier ist ein Rätsel, aber gehen wir zum Ende der Broschüre über:



Hier ist 2 die Kirchennummer, die zum Beispiel durch das Muster two[a_] [b_] → a[a[b]] . Beachten Sie, dass dies tatsächlich die Form der zweiten Zeile ist, wenn a als Function[r,r[]] und b als q behandelt wird . Wir erwarten also, dass das Ergebnis der Berechnungen wie folgt sein wird:



Trotzdem kann der Ausdruck [b] , der im Inneren liegt, als x geschrieben werden (unterscheidet sich wahrscheinlich von x, das zuvor auf dem Blatt geschrieben wurde) - als Ergebnis erhalten wir das Endergebnis:



Wir können also ein wenig entschlüsseln, was auf diesem Blatt passiert, aber mindestens ein Rätsel, das noch übrig bleibt, ist das, was Y sein sollte.

Tatsächlich hat die kombinatorische Logik einen Standard-Y-Kombinator: den sogenannten Festpunktkombinator . Formal wird es durch die Tatsache definiert, dass Y [ f ] gleich f [Y [ f ]] sein muss, oder mit anderen Worten, Y [ f ] ändert sich nicht, wenn f angewendet wird, also ist dies ein fester Punkt für f . (Der Y-Kombinator ist in der Wolfram-Sprache mit # 0 verknüpft.)

Derzeit ist der Y-Kombinator dank des Startbeschleunigers Y-Combinator , des sogenannten Paul Graham, bekannt geworden (der lange Zeit ein Fan der funktionalen Programmierung und der LISP-Programmiersprache war und den ersten auf dieser Sprache basierenden Webshop implementierte). Er sagte mir einmal persönlich: " Niemand versteht, was Y ein Kombinator ist ." (Es sollte beachtet werden, dass Y Combinator genau das ist, was es Unternehmen ermöglicht, Festkommaoperationen zu vermeiden ...)

Der Y-Kombinator (wie ein Festkomma-Kombinator) wurde mehrfach erfunden. Turing kam 1937 wirklich auf die Idee, die er Θ nannte. Aber ist der Buchstabe „Y“ auf unserer Seite ein berühmter Festkomma-Kombinator? Vielleicht auch nicht. Also, was ist unser "Y"? Betrachten Sie diese Reduzierung:



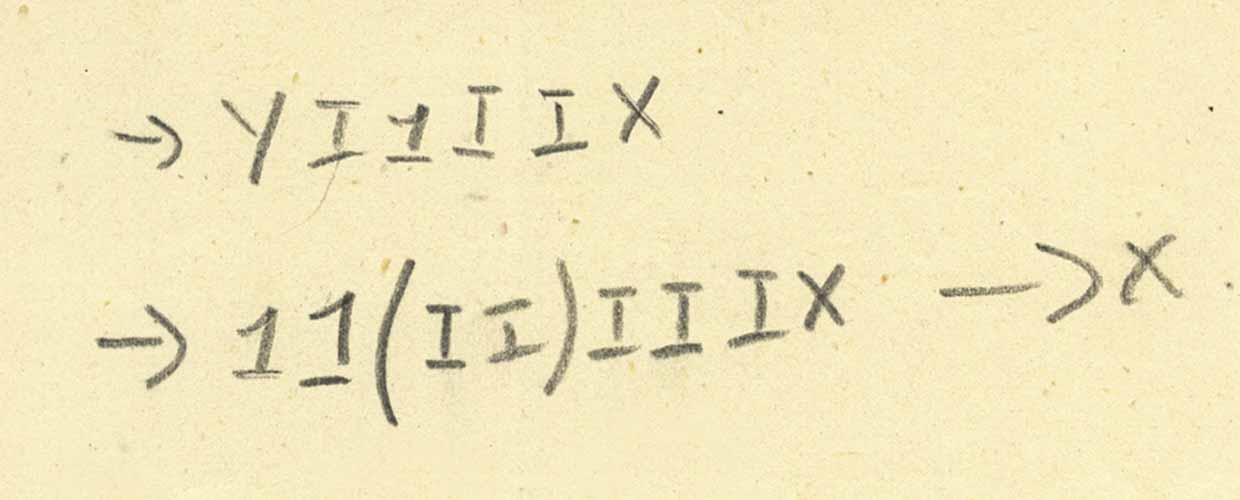
Diese Informationen reichen jedoch eindeutig nicht aus, um eindeutig zu bestimmen, was Y ist. Es ist klar, dass Y nicht nur mit einem Argument arbeitet. Es scheint, dass es sich um mindestens zwei Argumente handelt, aber es ist (zumindest für mich) unklar, wie viele Argumente für die Eingabe benötigt werden und was sie tun.

Schließlich müssen wir, obwohl wir in vielen Teilen der Broschüre einen Sinn erkennen können, sagen, dass auf globaler Ebene nicht klar ist, was damit geschehen ist. Obwohl es viele Erklärungen für das, was auf dem Blatt dargestellt ist, erfordert, ist es in der Lambda-Rechnung und unter Verwendung von Kombinatoren ziemlich elementar.

Vermutlich wird hier versucht, ein einfaches „Programm“ zu erstellen - mit Lambda-Kalkül und Kombinatoren, um etwas zu tun. Soweit dies jedoch für das Reverse Engineering typisch ist, fällt es uns schwer zu sagen, was dieses „Etwas“ sein sollte und was ein gemeinsames „erklärbares“ Ziel ist.

Auf dem Blatt wird noch eine weitere Funktion vorgestellt, die es wert ist, hier erwähnt zu werden - die Verwendung verschiedener Arten von Klammern. In der traditionellen Mathematik werden Klammern hauptsächlich für alles verwendet - und für Anwendungen einer Funktion (wie in f (x) ) und für Gruppierungen von Mitgliedern (wie in (1 + x) (1-x) oder weniger offensichtlich für a ( 1-x). x) ). (In Wolfram Language trennen wir die verschiedenen Verwendungen von Klammern - in eckigen Klammern, um f [x] -Funktionen zu definieren - und Klammern werden nur zur Gruppierung verwendet.)

Als der Lambda-Kalkül zum ersten Mal auftauchte, gab es viele Fragen zur Verwendung von Klammern. Später schrieb Alan Turing eine ganze (unveröffentlichte) Arbeit mit dem Titel " Transforming the mathematical form of notation and phraseology ", aber bereits 1937 hatte er das Gefühl, moderne (eher hackerartige) Definitionen für die Lambda-Rechnung (aus der übrigens hervorgegangen ist) zu beschreiben für die Kirche).

Er sagte, dass f, das auf g angewendet wird, geschrieben werden sollte {f} (g) , es sei denn, f ist das einzige Zeichen. In diesem Fall könnte es f (g) sein . Er sagte dann, dass Lambda (wie in Function[a, b] ) als λ a [ b ] oder alternativ als λ a geschrieben werden sollte . b .

Vielleicht wurde jedoch bis 1940 die ganze Idee, {...} und [...] zur Bezeichnung verschiedener Objekte zu verwenden, verworfen, hauptsächlich zugunsten von Klammern in einem mathematischen Standardstil.

Schauen Sie oben auf der Seite nach:



In dieser Form ist es schwer zu verstehen. In den Kirchendefinitionen sind eckige Klammern für die Gruppierung vorgesehen, wobei eine öffnende Klammer einen Punkt ersetzt. Anhand dieser Definition wird deutlich, dass Q (eventuell als D bezeichnet), das am Ende in Klammern steht, das gesamte anfängliche Lambda ist.

Tatsächlich schränkt die eckige Klammer hier den Körper des Lambda nicht ein; Stattdessen stellt es tatsächlich eine andere Anwendung der Funktion dar, und es gibt keinen expliziten Hinweis darauf, wo der Lambda-Körper endet. Am Ende ist zu sehen, dass der „mysteriöse Wissenschaftler“ die schließende eckige Klammer in eine runde Klammer geändert hat, wodurch die Definition von Church effektiv angewendet wurde - und er gezwungen wurde, den Ausdruck zu berechnen, wie auf dem Blatt gezeigt.

Also, was bedeutet dieses kleine Stück überhaupt? Ich denke, dies deutet darauf hin, dass die Seite in den 1930er Jahren oder nicht zu lange danach geschrieben wurde, da sich die Legende für die Klammern noch nicht beruhigt hatte.

Also, wessen Handschrift war es?

Vorher haben wir also darüber gesprochen, was auf der Seite geschrieben steht. Aber was ist mit dem, der es trotzdem geschrieben hat?

Der naheliegendste Kandidat für diese Rolle wäre Alan Turing selbst, schließlich befand sich die Seite in seinem Buch. Inhaltlich scheint es nichts Unvereinbares mit der Tatsache zu geben, dass Alan Turing dies schreiben könnte - selbst in dem Moment, als er anfing, sich mit Lambda-Kalkül zu befassen, nachdem er Anfang 1936 den Artikel der Kirche erhalten hatte.

Wie wäre es mit Handschrift? Gehört es Alan Turing? Betrachten wir einige überlebende Samples, die, wie wir sicher wissen, von Alan Turing geschrieben wurden:



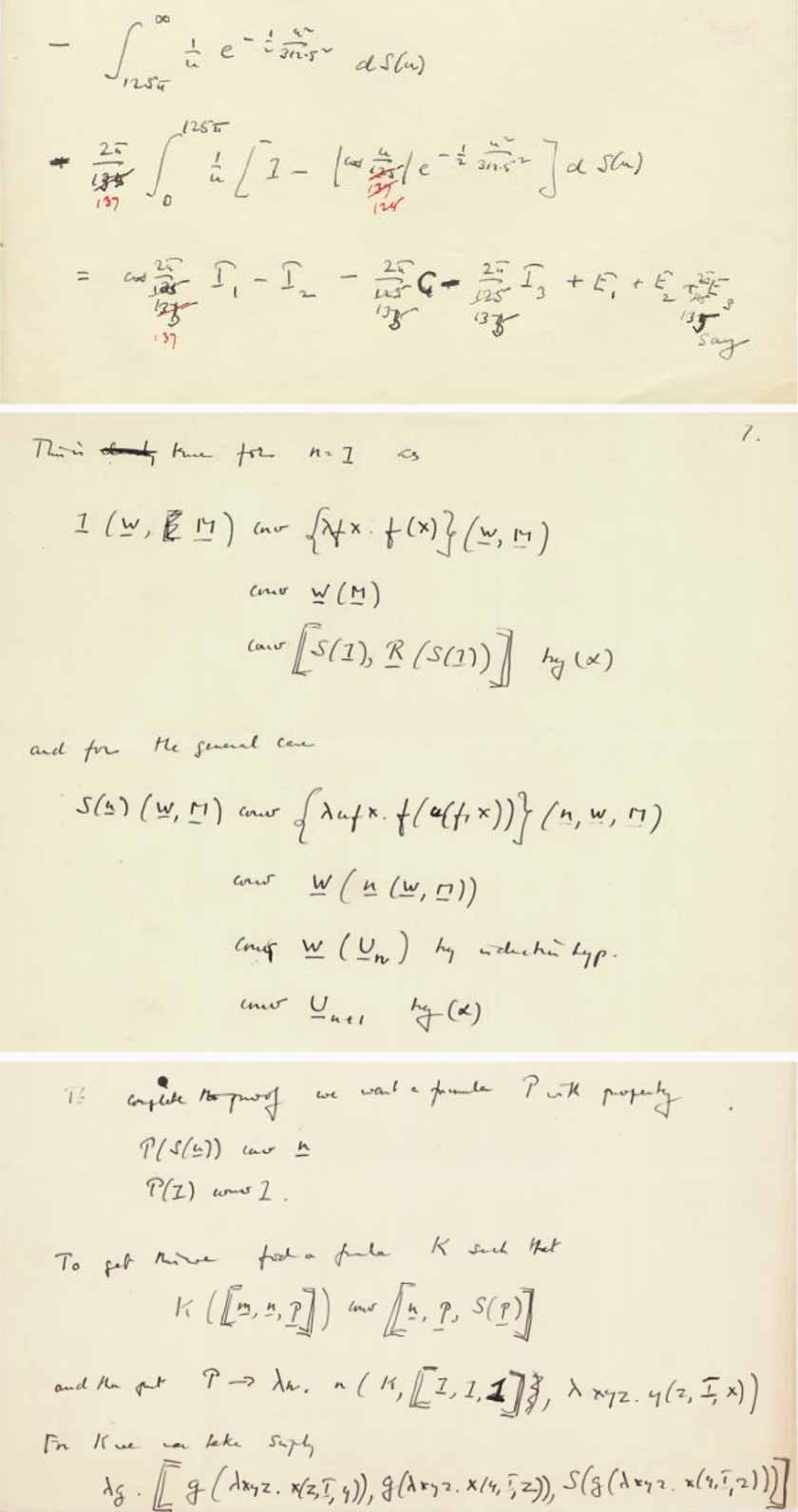
Der präsentierte Text sieht deutlich anders aus, aber was ist mit der im Text verwendeten Notation? Zumindest sieht dies meiner Meinung nach nicht so offensichtlich aus - und es kann davon ausgegangen werden, dass ein Unterschied dadurch verursacht werden kann, dass die vorhandenen Muster (die in den Archiven präsentiert werden) sozusagen „im Ziel“ geschrieben sind, während unsere Eine Seite ist ein Spiegelbild der Gedankenarbeit.

Für unsere Untersuchung stellte sich heraus, dass es eine Seite im Turing-Archiv gab, auf der er eine für die Notation erforderliche Zeichentabelle schrieb. Und wenn ich diese Zeichen Buchstabe für Buchstabe vergleiche, sehen sie mir ziemlich ähnlich (diese Aufzeichnungen wurden während Turings Zeit gemacht, als er das Pflanzenwachstum studierte , daher erschien die Notiz „Blattfläche“):



Ich wollte dies genauer untersuchen und schickte Proben an Sheila Lowe , eine professionelle Handschriftexpertin (und Handschriftautorin), die ich einmal getroffen hatte. Ich präsentierte nur unsere Broschüre als „Probe A“ und Turings vorhandene Handschrift als Probe B Ihre Antwort war endgültig und negativ: „ Der Schreibstil ist völlig anders. Was die Persönlichkeit betrifft, so hat der Autor von Probe „B“ eine schnellere und intuitivere Denkweise als der Autor von Probe „A “. “

Davon war ich noch nicht ganz überzeugt, entschied aber, dass es Zeit war, nach anderen Optionen zu suchen.

Wenn sich herausstellt, dass Turing dies nicht geschrieben hat, wer hat es dann getan? Norman Rutledge erzählte mir, dass er das Buch von Robin Gandhi erhalten habe, der Turings Testamentsvollstrecker war. Also habe ich "Probe" C "" von Gandhi geschickt:



Aber Sheilas erste Schlussfolgerung war, dass die drei Samples wahrscheinlich von drei verschiedenen Personen geschrieben wurden, wobei erneut angemerkt wurde, dass das Sample "B" vom " schnellsten Denker" stammt - demjenigen, der höchstwahrscheinlich gerne nach ungewöhnlichen Lösungen für Probleme sucht. . (Ich finde es angenehm, dass ein moderner Handschriftspezialist eine solche Einschätzung von Turings Handschrift abgeben würde, wenn man bedenkt, wie aktiv sich jeder in Turings Schulaufgaben der 1920er Jahre über seine Handschrift beschwert).

Nun, in diesem Moment schienen sowohl Turing als auch Gandhi von der Liste der "Verdächtigen" ausgeschlossen zu sein. Wer könnte das schreiben? Ich begann an Leute zu denken, denen Turing sein Buch leihen konnte. Gleichzeitig sollten sie natürlich in der Lage sein, Berechnungen mit Lambda-Kalkül durchzuführen.

Ich schlug vor, dass die Person aus Cambridge oder zumindest aus England kommen sollte, da das Wasserzeichen auf Papier angegeben ist. Ich habe die Arbeitshypothese falsch verstanden, dass 1936 oder so der richtige Zeitpunkt war, dies zu schreiben. Wen kannte er damals und mit wem kommunizierte Turing? . ( 13 , 1930 1936 .)

. , , , — 1933 , («» ) : 0.12345678910111213… ( 1, 2, 3, 4 ,…, 8, 9, 10, 11, 12,…, , «» , ).

1937 - , , . ( , - ).

, ( ) , . ( , 1948 Turbochamp — , , ).

? LinkedIn, , , Microsoft. , , . ( ):



, ( f . .)

? , . « », , . ( , , , , , ).

— , .

«»

, . , , , , , .

, -, ? 1946 (, ). 1949 , . 1954 , . , 1957 . , (, , , , . .). 1960 , ( ) ( ), , .

? - (, , , 2005 , «»). , « ».

- , , , ? . , - - - . , 1955 « » ( , BooleanMinimize ). , ( «NAR», «NAR…», , «NARLAB» — «» ). .

. , , , « ». , , , , 1954 , . , , .

, « ( , ) » « , , , , [ ] ». , ? . ( , , , 1902 , « » : « »).

, , , , , 12 , -, , , 21 ).

, , - . , - . , , , 1938 . 2000 - ( ) — , , 2002 , .

, , ? , , . :



, . , , , , , .

: ? , , , .

- , — 1940 — . , 1944 , , . , , .

, , , , 1952 , « » . , , , , — , , . , . , , , , . , 1980- , “ » — , , , . ( , , , , « , »). , « , , , — … », , « ».)

, , . . , « » (. . -), -.

. 1969 , , , , , .
, , . . — — . . - , , .

1995 , . — . . , , — , , , . , , , , , 24 . ( 2001 — 45 ).

, ? , , , , , ( , , , c ). ( ) « » ( ), , -, , . , .

, . , 30 , . , , , - — , , , (, , , Mathematica ). , , , , , , , . , , , .

? , , () , . ( , .) , 1 . , .

, , . : « ! » , . . , -, , , .

, , , , , . , : . ; .

, . , ? - , 1930- . , , , - 1940- . , . , , , , , -.

, - , , , . , , , , , , . , , — , , …

: ( ), ( ) ( ).

Wolfram Language?
.
Anmeldung für neue Kurse . Online-Kurs fertig.
Wolfram Language.