Lösen Sie die Gleichung der einfachen linearen Regression

Der Artikel beschreibt verschiedene Methoden zur Bestimmung der mathematischen Gleichung einer einfachen (paarweisen) Regressionslinie.

Alle hier diskutierten Methoden zur Lösung der Gleichung basieren auf der Methode der kleinsten Quadrate. Wir bezeichnen die Methoden wie folgt:

• Analytische Lösung
• Gefälle
• Stochastische Gefälleabfahrt

Für jede der Methoden zum Lösen der Gleichung der geraden Linie werden im Artikel verschiedene Funktionen beschrieben, die hauptsächlich in solche unterteilt sind, die ohne die NumPy- Bibliothek geschrieben wurden, und solche, die NumPy für Berechnungen verwenden. Man geht davon aus, dass der geschickte Einsatz von NumPy die Rechenkosten senkt.

Der gesamte Code in diesem Artikel wurde in Python 2.7 mit dem Jupyter Notebook geschrieben . Quellcode und Beispieldatendatei auf github

Der Artikel konzentriert sich mehr auf Anfänger und diejenigen, die bereits begonnen haben, das Studium eines sehr umfangreichen Abschnitts in künstlicher Intelligenz - maschinelles Lernen - zu beherrschen.

Zur Veranschaulichung des Materials verwenden wir ein sehr einfaches Beispiel.

Beispielbedingungen

Wir haben fünf Werte, die die Abhängigkeit von Y von X charakterisieren (Tabelle Nr. 1):

Tabelle Nr. 1 "Bedingungen des Beispiels"



Wir gehen davon aus, dass die Werte $$$x_i$ Ist der Monat des Jahres und $$$y_i$ - Einnahmen in diesem Monat. Mit anderen Worten, der Umsatz hängt vom Monat des Jahres ab und $$$x_i$ - das einzige Zeichen, von dem die Einnahmen abhängen.

Ein gutes Beispiel ist die bedingte Abhängigkeit der Einnahmen vom Monat des Jahres und die Anzahl der Werte - es gibt nur sehr wenige. Diese Vereinfachung ermöglicht es jedoch, das, was an den Fingern genannt wird, nicht immer leicht zu erklären, welches Material von Anfängern aufgenommen wird. Und auch die Einfachheit der Zahlen ermöglicht es denjenigen, die das Beispiel auf Papier lösen möchten, ohne nennenswerte Arbeitskosten.

Angenommen, die im Beispiel gezeigte Abhängigkeit kann durch die mathematische Gleichung einer einfachen (paarweisen) Regressionslinie der Form ziemlich gut angenähert werden:

$$

$$Y = a + bx$$

wo $$$x$ - Dies ist der Monat, in dem die Einnahmen eingegangen sind. $$$Y$ - Einnahmen entsprechend dem Monat, $$$a$ und $$$b$ - Regressionskoeffizienten der geschätzten Linie.

Beachten Sie, dass der Koeffizient $$$b$ oft als Steigung oder Gradient der geschätzten Linie bezeichnet; stellt den Betrag dar, um den geändert werden soll $$$Y$ beim wechseln $$$x$ .

Offensichtlich besteht unsere Aufgabe im Beispiel darin, solche Koeffizienten in der Gleichung auszuwählen $$$a$ und $$$b$ für die die Abweichungen unserer geschätzten monatlichen Einnahmen von den tatsächlichen Antworten, d.h. Die in der Stichprobe angegebenen Werte sind minimal.

Methode der kleinsten Quadrate

Nach der Methode der kleinsten Quadrate sollte die Abweichung durch Quadrieren berechnet werden. Eine solche Technik vermeidet die gegenseitige Rückzahlung von Abweichungen, wenn sie entgegengesetzte Vorzeichen haben. Wenn beispielsweise in einem Fall die Abweichung +5 (plus fünf) und in dem anderen -5 (minus fünf) beträgt, wird die Summe der Abweichungen gegenseitig zurückgezahlt und beträgt 0 (Null). Sie können die Abweichung nicht verschwenden, sondern die Moduleigenschaft verwenden. Dann sind alle Abweichungen positiv und häufen sich in uns an. Wir werden nicht im Detail auf diesen Punkt eingehen, sondern lediglich darauf hinweisen, dass es zur Vereinfachung der Berechnungen üblich ist, die Abweichung zu quadrieren.

So sieht die Formel aus, mit deren Hilfe wir die kleinste Summe der quadratischen Abweichungen (Fehler) ermitteln:

$$

$$ERR (x) = \ Summe \ Grenzen_ {i = 1} ^ n (a + bx_i - y_i) ^ 2 = \ Summe \ Grenzen_ {i = 1} ^ n (f (x_i) -y_i) ^ 2 \ rechter Pfeil min$$

wo $$$f (x_i) = a + bx_i$ Ist eine Funktion der Annäherung an wahre Antworten (d. H. Von uns berechnete Einnahmen),

$$$y_i$ - Dies sind echte Antworten (Einnahmen in der Stichprobe),

$$$i$ Ist der Stichprobenindex (die Nummer des Monats, in dem die Abweichung bestimmt wird)

Wir differenzieren die Funktion, definieren die partiellen Differentialgleichungen und sind bereit, mit der analytischen Lösung fortzufahren. Aber lassen Sie uns zunächst einen kurzen Exkurs über die Unterscheidung machen und die geometrische Bedeutung der Ableitung in Erinnerung rufen.

Differenzierung

Differenzierung ist die Operation des Findens der Ableitung einer Funktion.

Wofür ist ein Derivat? Die Ableitung einer Funktion kennzeichnet die Änderungsrate einer Funktion und gibt deren Richtung an. Wenn die Ableitung an einem bestimmten Punkt positiv ist, nimmt die Funktion zu, andernfalls nimmt die Funktion ab. Und je größer der Wert der Ableitung modulo ist, desto höher ist die Änderungsrate der Werte der Funktion und desto steiler ist der Winkel des Graphen der Funktion.

Beispielsweise bedeutet unter den Bedingungen des kartesischen Koordinatensystems der Wert der Ableitung am Punkt M (0,0) gleich +25 , dass an einem gegebenen Punkt der Wert verschoben wird $$$x$ Recht auf beliebige Einheit, Wert $$$y$ erhöht sich um 25 konventionelle Einheiten. In der Grafik sieht es nach einem ziemlich steilen Höhenwinkel aus $$$y$ von einem bestimmten Punkt.

Ein weiteres Beispiel. Ein abgeleiteter Wert von -0,1 bedeutet, dass beim Versatz $$$x$ pro konventionelle Einheit, Wert $$$y$ sinkt nur um 0,1 konventionelle Einheit. Gleichzeitig können wir im Funktionsgraphen eine kaum wahrnehmbare Neigung nach unten beobachten. Wenn wir eine Analogie zum Berg ziehen, scheinen wir den sanften Abhang des Berges sehr langsam hinunterzufahren, im Gegensatz zum vorherigen Beispiel, wo wir sehr steile Gipfel nehmen mussten :)

Also nach Differenzierung der Funktion $$$ERR (x) = \ sum \ limits_ {i = 1} ^ n (a + bx_i - y_i) ^ 2$ durch Koeffizienten $$$a$ und $$$b$ Wir definieren die Gleichungen von partiellen Ableitungen erster Ordnung. Nachdem wir die Gleichungen definiert haben, erhalten wir ein System aus zwei Gleichungen, die entscheiden, welche Werte für die Koeffizienten wir wählen können $$$a$ und $$$b$ bei denen sich die Werte der entsprechenden Ableitungen an gegebenen Punkten um einen sehr, sehr kleinen Wert ändern und sich bei der analytischen Lösung überhaupt nicht ändern. Mit anderen Worten, die Fehlerfunktion bei den gefundenen Koeffizienten erreicht ein Minimum, da die Werte der partiellen Ableitungen an diesen Punkten Null sind.

Also nach den Differenzierungsregeln die Gleichung der partiellen Ableitung 1. Ordnung in Bezug auf den Koeffizienten $$$a$ wird die Form annehmen:

$$

$$2na + 2b \ Summe \ Grenzen_ {i = 1} ^ nx_i - 2 \ Summe \ Grenzen_ {i = 1} ^ ny_i = 2 (na + b \ Summe \ Grenzen_ {i = 1} ^ nx_i - \ Summe \ Grenzen_ {i = 1} ^ ny_i)$$

Teilableitungsgleichung 1. Ordnung in Bezug auf $$$b$ wird die Form annehmen:

$$

$$2a \ sum \ limits_ {i = 1} ^ nx_i + 2b \ sum \ limits_ {i = 1} ^ nx ^ 2_i - 2 \ sum \ limits_ {i = 1} ^ nx_iy_i = 2 \ sum \ limits_ {i = 1} ^ nx_i (a + b \ sum \ limits_ {i = 1} ^ nx_i - \ sum \ limits_ {i = 1} ^ ny_i)$$

Als Ergebnis haben wir ein Gleichungssystem erhalten, das eine ziemlich einfache analytische Lösung bietet:

\ begin {equation *}
\ begin {cases}
na + b \ sum \ limits_ {i = 1} ^ nx_i - \ sum \ limits_ {i = 1} ^ ny_i = 0
\\
\ sum \ limit_ {i = 1} ^ nx_i (a + b \ sum \ limit_ {i = 1} ^ nx_i - \ sum \ limit_ {i = 1} ^ ny_i) = 0
\ end {Fälle}
\ end {Gleichung *}

Überprüfen Sie vor dem Lösen der Gleichung das korrekte Laden und formatieren Sie die Daten.

Daten herunterladen und formatieren

Es ist zu beachten, dass wir den Code für die analytische Lösung und später für den Gradienten- und den stochastischen Gradientenabstieg in zwei Variationen verwenden werden: Verwenden der NumPy- Bibliothek und ohne Verwendung müssen wir die Daten entsprechend formatieren (siehe Code).

Visualisierung

Nachdem wir nun erstens die Daten heruntergeladen, zweitens das korrekte Laden überprüft und schließlich die Daten formatiert haben, werden wir die erste Visualisierung durchführen. Oft wird hierfür die Pairplot- Methode der Seaborn- Bibliothek verwendet. In unserem Beispiel ist es aufgrund der begrenzten Anzahl nicht sinnvoll, die Seaborn- Bibliothek zu verwenden. Wir werden die reguläre Matplotlib-Bibliothek verwenden und nur das Streudiagramm betrachten.


Anhang Nr. 1 „Abhängigkeit der Einnahmen vom Monat des Jahres“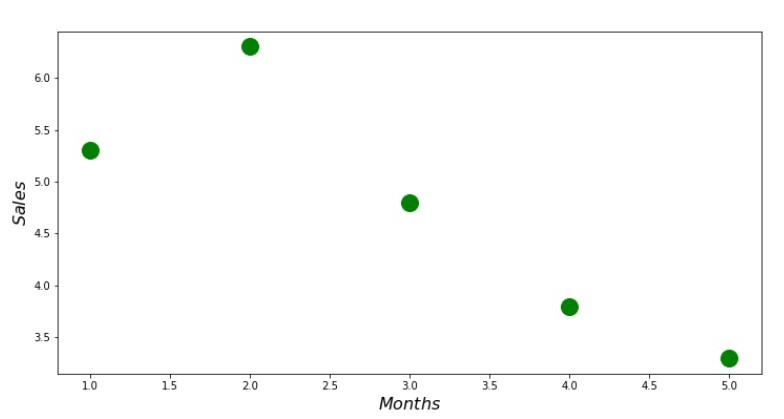

Analytische Lösung

Wir werden die gebräuchlichsten Werkzeuge in Python verwenden und das Gleichungssystem lösen:

\ begin {Gleichung *}
\ begin {Fälle}
na + b \ sum \ limits_ {i = 1} ^ nx_i - \ sum \ limits_ {i = 1} ^ ny_i = 0
\\
\ sum \ limits_ {i = 1} ^ nx_i (a + b \ sum \ limits_ {i = 1} ^ nx_i - \ sum \ limits_ {i = 1} ^ ny_i) = 0
\ end {Fälle}
\ end {Gleichung *}

Gemäß der Cramer-Regel finden wir eine gemeinsame Determinante sowie Determinanten von $$$a$ und von $$$b$ Danach wird die Determinante durch geteilt $$$a$ auf der gemeinsamen Determinante - wir finden den Koeffizienten $$$a$ Finden Sie in ähnlicher Weise den Koeffizienten $$$b$ .


Folgendes haben wir:



Wenn die Koeffizientenwerte gefunden sind, wird die Summe der quadratischen Abweichungen eingestellt. Wir zeichnen eine gerade Linie auf dem Streuhistogramm in Übereinstimmung mit den gefundenen Koeffizienten.


Plan Nr. 2 „Richtige und geschätzte Antworten“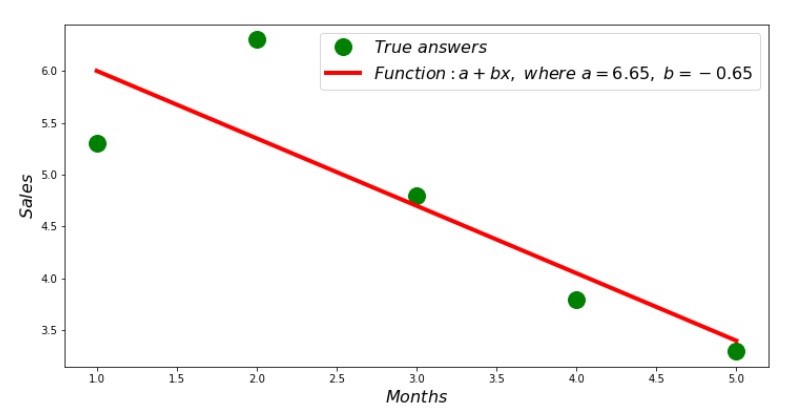



Sie können den Abweichungsplan für jeden Monat anzeigen. In unserem Fall können wir keinen signifikanten praktischen Wert daraus ziehen, aber wir werden die Neugier befriedigen, wie gut die einfache lineare Regressionsgleichung die Abhängigkeit des Umsatzes vom Monat des Jahres charakterisiert.


Anhang Nr. 3 „Abweichungen,%“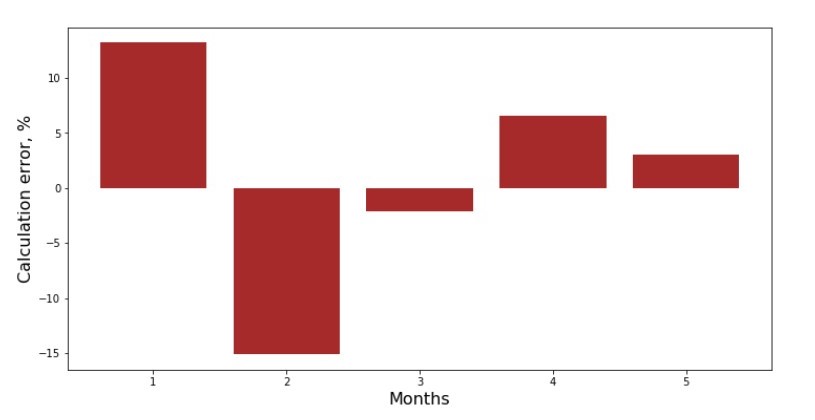



Nicht perfekt, aber wir haben unsere Aufgabe erfüllt.

Wir schreiben eine Funktion zur Bestimmung der Koeffizienten $$$a$ und $$$b$ verwendet die NumPy- Bibliothek, genauer gesagt, schreiben wir zwei Funktionen: eine unter Verwendung einer pseudo-inversen Matrix (in der Praxis nicht empfohlen, da der Prozess rechnerisch komplex und instabil ist), die andere unter Verwendung einer Matrixgleichung.


Vergleichen Sie die zur Bestimmung der Koeffizienten benötigte Zeit $$$a$ und $$$b$ gemäß den 3 vorgestellten Methoden.




Auf einer kleinen Datenmenge wird eine "selbstgeschriebene" Funktion angezeigt, die die Koeffizienten unter Verwendung der Cramer-Methode ermittelt.

Jetzt können Sie mit anderen Methoden zum Ermitteln der Koeffizienten fortfahren $$$a$ und $$$b$ .

Gefälle

Definieren wir zunächst, was ein Farbverlauf ist. Ein Gradient ist auf einfache Weise ein Segment, das die Richtung des maximalen Wachstums einer Funktion angibt. In Analogie zu einem Anstieg bergauf, wo die Steigung aussieht, gibt es den steilsten Anstieg auf den Gipfel des Berges. Bei der Entwicklung des Bergbeispiels erinnern wir uns, dass wir tatsächlich den steilsten Abstieg benötigen, um das Tiefland so schnell wie möglich zu erreichen, dh das Minimum - den Ort, an dem die Funktion nicht zunimmt oder abnimmt. Zu diesem Zeitpunkt ist die Ableitung Null. Wir brauchen also keinen Farbverlauf, sondern einen Anti-Farbverlauf. Um den Anti-Gradienten zu finden, müssen Sie nur den Gradienten mit -1 (minus eins) multiplizieren.

Wir machen darauf aufmerksam, dass eine Funktion mehrere Minima haben kann und dass wir, nachdem wir gemäß dem unten vorgeschlagenen Algorithmus in eines davon gesunken sind, kein anderes Minimum finden können, das möglicherweise niedriger ist als das gefundene. Entspannen Sie sich, wir sind nicht in Gefahr! In unserem Fall haben wir es mit einem einzigen Minimum zu tun, da unsere Funktion $$$\ sum \ limit_ {i = 1} ^ n (a + bx_i - y_i) ^ 2$ In der Grafik ist eine gewöhnliche Parabel. Und wie wir alle aus dem Mathematikkurs sehr gut wissen sollten, hat die Parabel nur ein Minimum.

Nachdem wir herausgefunden haben, warum wir einen Gradienten benötigen, und auch, dass der Gradient ein Segment ist, dh ein Vektor mit gegebenen Koordinaten, die genau dieselben Koeffizienten sind $$$a$ und $$$b$ Wir können einen Gradientenabstieg implementieren.

Bevor ich anfange, empfehle ich, nur ein paar Sätze über den Abstiegsalgorithmus zu lesen:

• Wir bestimmen die Koordinaten der Koeffizienten pseudozufällig $$$a$ und $$$b$ . In unserem Beispiel werden wir die Koeffizienten nahe Null bestimmen. Dies ist eine übliche Praxis, aber jede Praxis kann ihre eigene Praxis haben.
• Von der Koordinate $$$a$ subtrahieren Sie den Wert der partiellen Ableitung 1. Ordnung am Punkt $$$a$ . Wenn also die Ableitung positiv ist, erhöht sich die Funktion. Wenn wir also den Wert der Ableitung wegnehmen, bewegen wir uns in die entgegengesetzte Wachstumsrichtung, dh in die Abstiegsrichtung. Wenn die Ableitung negativ ist, nimmt die Funktion an diesem Punkt ab und der Wert der Ableitung wird weggenommen. Wir bewegen uns in Richtung Abstieg.
• Wir führen eine ähnliche Operation mit der Koordinate durch $$$b$ : subtrahieren Sie den Wert der partiellen Ableitung am Punkt $$$b$ .
• Um nicht das Minimum zu springen und nicht in den fernen Raum zu fliegen, muss die Schrittweite in Richtung Abstieg eingestellt werden. Im Allgemeinen können Sie einen ganzen Artikel darüber schreiben, wie Sie den Schritt richtig einstellen und während des Abstiegs ändern, um die Berechnungskosten zu senken. Aber jetzt haben wir eine etwas andere Aufgabe, und wir werden die Schrittweite durch die wissenschaftliche Methode des "Stocherns" oder, wie es bei gewöhnlichen Menschen heißt, empirisch bestimmen.
• Nachdem wir von den angegebenen Koordinaten sind $$$a$ und $$$b$ Subtrahiert man die Werte der Ableitungen, erhält man neue Koordinaten $$$a$ und $$$b$ . Wir gehen den nächsten Schritt (Subtraktion) bereits von den berechneten Koordinaten aus. Und so beginnt der Zyklus immer wieder, bis die erforderliche Konvergenz erreicht ist.

Das ist alles! Jetzt sind wir auf der Suche nach der tiefsten Schlucht des Marianengrabens. Runterkommen.




Wir stürzten auf den Grund des Marianengrabens und fanden dort alle gleichen Werte der Koeffizienten $$$a$ und $$$b$ , was in der Tat zu erwarten war.

Lassen Sie uns einen weiteren Tauchgang machen, nur dieses Mal wird die Befüllung unseres Tiefseefahrzeugs durch andere Technologien erfolgen, nämlich die NumPy- Bibliothek.



Koeffizientenwerte $$$a$ und $$$b$ unveränderlich.

Schauen wir uns an, wie sich der Fehler beim Gefälle verändert hat, dh wie sich die Summe der quadratischen Abweichungen mit jedem Schritt verändert hat.


Grafik №4 „Die Summe der Abweichungsquadrate beim Gradientenabstieg“



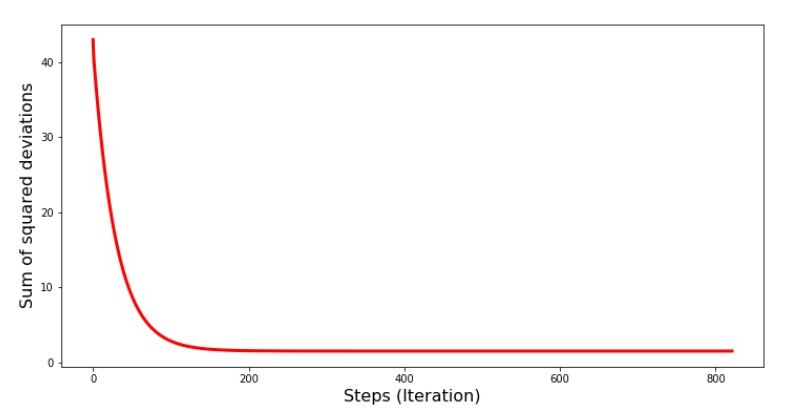
In der Grafik sehen wir, dass mit jedem Schritt der Fehler abnimmt und nach einer bestimmten Anzahl von Iterationen eine praktisch horizontale Linie beobachtet wird.

Schließlich schätzen wir den Unterschied in der Ausführungszeit des Codes:




Vielleicht machen wir etwas falsch, aber auch hier ist eine einfache "selbstgeschriebene" Funktion, die die NumPy- Bibliothek nicht verwendet, der Zeit voraus, die die NumPy- Bibliothek verwendet.

Wir stehen aber nicht still, sondern befassen uns mit der Untersuchung eines anderen aufregenden Weges zur Lösung der Gleichung der einfachen linearen Regression. Triff mich!

Stochastischer Gradientenabstieg

Um das Funktionsprinzip des stochastischen Gradientenabfalls schnell zu verstehen, ist es besser, seine Unterschiede zum normalen Gradientenabstieg zu bestimmen. Wir, im Fall des Gradientenabfalls, in den Gleichungen der Ableitungen von $$$a$ und $$$a$ verwendete die Summe der Werte aller Zeichen und der wahren Antworten, die in der Stichprobe verfügbar sind (d. h. die Summe aller $$$x_i$ und $$$y_i$ ) Beim stochastischen Gradientenabstieg werden nicht alle in der Stichprobe verfügbaren Werte verwendet, sondern pseudozufällig der sogenannte Stichprobenindex ausgewählt und dessen Werte verwendet.

Wenn der Index beispielsweise durch die Zahl 3 (drei) bestimmt wird, nehmen wir die Werte $$$x_3 = 3$ und $$$y_3 = $ 4.$ , dann setzen wir die Werte in die Ableitungsgleichungen ein und bestimmen die neuen Koordinaten. Nachdem wir die Koordinaten bestimmt haben, bestimmen wir erneut pseudozufällig den Index der Stichprobe, ersetzen die dem Index entsprechenden Werte in den partiellen Differentialgleichungen und bestimmen die Koordinaten auf neue Weise $$$a$ und $$$a$ usw. vor der Ökologisierung der Konvergenz. Auf den ersten Blick mag es so aussehen, als könnte dies funktionieren, aber es funktioniert. Es ist wahr, dass nicht mit jedem Schritt der Fehler abnimmt, aber der Trend existiert sicherlich.

Was sind die Vorteile eines stochastischen Gradientenabfalls gegenüber dem üblichen? Wenn unsere Stichprobe sehr groß ist und in Zehntausenden von Werten gemessen wird, ist es viel einfacher zu verarbeiten, sagen wir, zufällig Tausende von ihnen als die gesamte Stichprobe. In diesem Fall wird der stochastische Gradientenabstieg gestartet. In unserem Fall werden wir natürlich keinen großen Unterschied bemerken.

Wir sehen uns den Code an.




Wir schauen uns die Koeffizienten genau an und beschäftigen uns mit der Frage „Wie?“. Wir haben andere Werte der Koeffizienten $$$a$ und $$$b$ . Vielleicht hat der stochastische Gradientenabstieg optimalere Parameter der Gleichung gefunden? Leider nein. Es reicht aus, die Summe der quadratischen Abweichungen zu betrachten und festzustellen, dass mit den neuen Werten der Koeffizienten der Fehler größer ist. Eile nicht zur Verzweiflung. Wir zeichnen die Fehleränderung auf.


Grafik №5 „Die Summe der Abweichungsquadrate beim stochastischen Gradientenabstieg“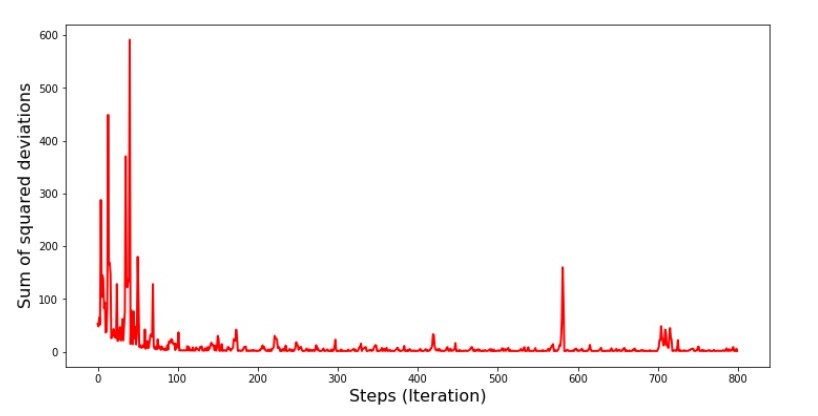



Nachdem wir uns den Zeitplan angesehen haben, passt alles zusammen und jetzt werden wir alles reparieren.

Also, was ist passiert? Folgendes ist passiert. Wenn wir einen Monat zufällig auswählen, versucht unser Algorithmus für den ausgewählten Monat, den Fehler bei der Berechnung des Umsatzes zu verringern.Dann wählen wir einen anderen Monat aus und wiederholen die Berechnung, aber wir reduzieren den Fehler bereits für den zweiten ausgewählten Monat. Lassen Sie uns nun daran erinnern, dass wir in den ersten zwei Monaten erheblich von der Linie der Gleichung der einfachen linearen Regression abgewichen sind. Dies bedeutet, dass unser Algorithmus den Fehler während der gesamten Stichprobe erheblich erhöht, wenn einer dieser beiden Monate ausgewählt und dann der Fehler jedes dieser Monate verringert wird. Was tun? Die Antwort ist einfach: Sie müssen die Abstiegsstufe reduzieren. Wenn Sie die Abstiegsstufe verringern, wird der Fehler auch nicht mehr auf- und abspringen. Vielmehr wird der Fehler "Überspringen" nicht aufhören, aber nicht so schnell :) Wir werden es überprüfen.




Grafik Nr. 6 „Die Summe der Abweichungsquadrate beim stochastischen Gradientenabstieg (80.000 Schritte)“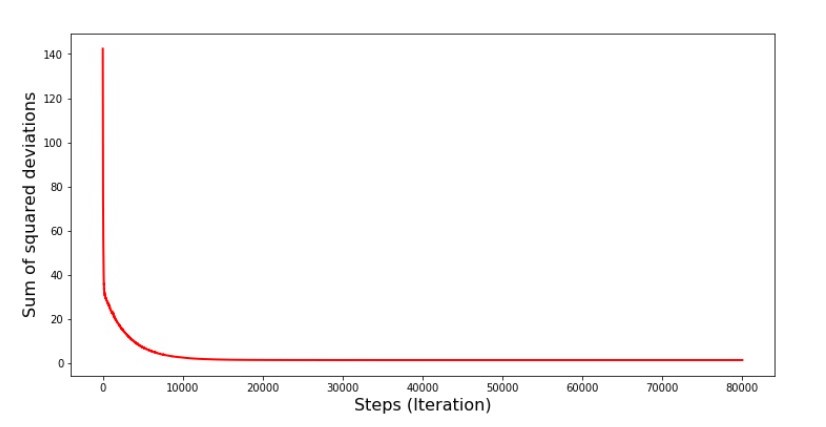



Die Werte der Koeffizienten verbesserten sich, waren aber immer noch nicht ideal. Hypothetisch kann dies auf diese Weise korrigiert werden. Zum Beispiel wählen wir bei den letzten 1000 Iterationen die Werte der Koeffizienten, mit denen der minimale Fehler gemacht wurde. Dazu müssen wir die Koeffizientenwerte selbst aufschreiben. Wir werden dies nicht tun, sondern den Zeitplan beachten. Es sieht glatt aus und der Fehler scheint gleichmäßig abzunehmen. Dies ist eigentlich nicht der Fall. Schauen wir uns die ersten 1000 Iterationen an und vergleichen sie mit den letzten.


№7 « SGD ( 1000 )»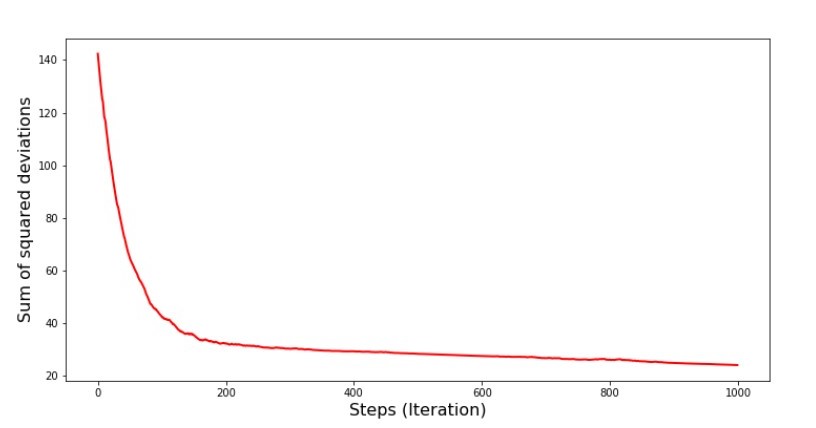



№8 « SGD ( 1000 )»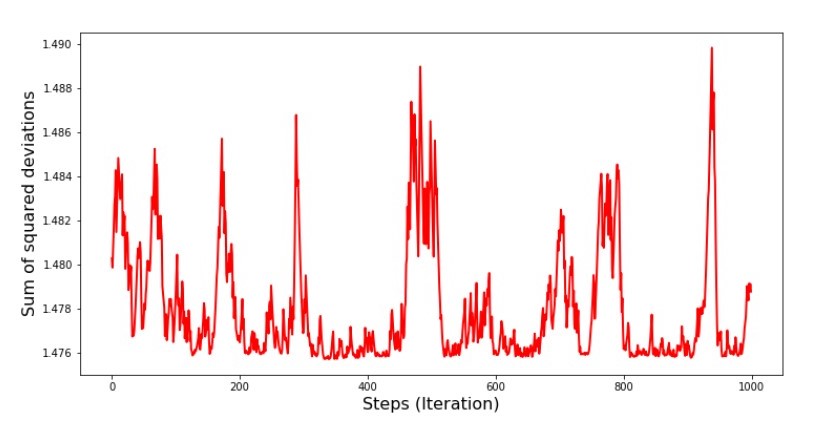



. , 1,475 , … , $$$a$ und $$b , und wählen Sie dann diejenigen aus, für die der Fehler minimal ist. Wir hatten jedoch ein ernsthafteres Problem: Wir mussten 80.000 Schritte (siehe Code) ausführen, um Werte nahe am Optimum zu erhalten. Und dies widerspricht bereits der Idee, Rechenzeit mit stochastischem Gradientenabstieg relativ zum Gradienten zu sparen. Was kann korrigiert und verbessert werden? Es ist nicht schwer zu bemerken, dass wir bei den ersten Iterationen zuversichtlich nach unten gehen, und daher sollten wir bei den ersten Iterationen einen großen Schritt lassen und den Schritt verringern, wenn wir vorwärts gehen. Wir werden dies in diesem Artikel nicht tun - es hat sich bereits in die Länge gezogen. Diejenigen, die dies wünschen, können sich überlegen, wie das geht, es ist nicht schwierig :)Jetzt werden wir mit derNumPy-Bibliothek einen stochastischen Gradientenabstieg durchführen$b$

(und wir werden nicht über die Steine ​​stolpern, die wir zuvor identifiziert haben)




Es stellte sich heraus, dass die Werte fast dieselben waren wie während des Abstiegs, ohne NumPy zu verwenden . Dies ist jedoch logisch.

Wir werden herausfinden, wie viel Zeit stochastische Gradientenabfahrten uns gekostet haben.




Je weiter im Wald, desto dunkler die Wolken: Auch hier zeigt die „selbstgeschriebene“ Formel das beste Ergebnis. All dies legt nahe, dass es noch subtilere Möglichkeiten zur Verwendung der NumPy- Bibliothek geben sollte , die die Berechnungsvorgänge wirklich beschleunigen. In diesem Artikel werden wir nichts darüber erfahren. Es gibt etwas zu denken in Ihrer Freizeit :)

Fassen Sie zusammen

Bevor ich zusammenfasse, möchte ich die Frage beantworten, die wahrscheinlich von unserem lieben Leser gestellt wurde. Warum in der Tat eine solche „Qual“ mit Abfahrten, warum müssen wir den Berg hinauf und hinunter gehen (hauptsächlich hinunter), um das geschätzte Tiefland zu finden, wenn wir ein so mächtiges und einfaches Gerät in der Hand haben, in Form einer analytischen Lösung, zu der wir uns sofort teleportieren Richtiger Ort?

Die Antwort auf diese Frage liegt an der Oberfläche. Jetzt haben wir ein sehr einfaches Beispiel untersucht, in dem die wahre Antwort$$y i hängt von einem Attribut ab$y_i$$$$x_i$ .Im Leben wird dies nicht oft gesehen. Stellen Sie sich also vor, wir haben Anzeichen von 2, 30, 50 oder mehr. Fügen Sie dazu Tausende oder sogar Zehntausende von Werten für jedes Attribut hinzu. In diesem Fall besteht die analytische Lösung den Test möglicherweise nicht und schlägt fehl. Der Gradientenabstieg und seine Variationen bringen uns langsam aber sicher näher an das Ziel - das Minimum der Funktion. Und machen Sie sich keine Sorgen um die Geschwindigkeit - wir werden wahrscheinlich auch Methoden analysieren, mit denen wir die Schrittlänge (d. H. Die Geschwindigkeit) einstellen und anpassen können.

Und nun eigentlich eine kurze Zusammenfassung.

Erstens hoffe ich, dass das in dem Artikel vorgestellte Material Anfängern dabei hilft, "Wissenschaftler zu datieren", um zu verstehen, wie die Gleichungen der einfachen (und nicht nur) linearen Regression gelöst werden können.

Zweitens haben wir verschiedene Möglichkeiten untersucht, um die Gleichung zu lösen. Nun können wir je nach Situation diejenige auswählen, die zur Lösung des Problems am besten geeignet ist.

Drittens haben wir die Kraft zusätzlicher Einstellungen gesehen, nämlich die Schrittlänge des Gradientenabfalls. Dieser Parameter kann nicht vernachlässigt werden. Wie oben erwähnt, sollte die Schrittlänge entlang des Abstiegs geändert werden, um die Berechnungskosten zu reduzieren.

Viertens zeigten in unserem Fall „selbstgeschriebene“ Funktionen das beste zeitliche Ergebnis der Berechnungen. Dies ist wahrscheinlich darauf zurückzuführen, dass die Funktionen der NumPy- Bibliothek nicht so professionell genutzt werden. Aber wie auch immer, die Schlussfolgerung lautet wie folgt. Einerseits lohnt es sich manchmal, etablierte Meinungen in Frage zu stellen, und andererseits lohnt es sich nicht immer, Dinge zu komplizieren - im Gegenteil, manchmal ist ein einfacherer Weg zur Lösung eines Problems effektiver. Und da unser Ziel darin bestand, drei Ansätze zur Lösung der Gleichung der einfachen linearen Regression zu analysieren, war die Verwendung von "selbstgeschriebenen" Funktionen für uns völlig ausreichend.

← Frühere Arbeiten des Autors - „Wir untersuchen die Aussage des zentralen Grenzwertsatzes anhand der Exponentialverteilung“$\leftarrow$
→ Die nächste Arbeit des Autors - "Wir bringen die Gleichung der linearen Regression in Matrixform"$\rightarrow$

Literatur (oder so ähnlich)

1. Lineare Regression

http://statistica.ru/theory/osnovy-lineynoy-regressii/

2. Die Methode der kleinsten Quadrate

mathprofi.ru/metod_naimenshih_kvadratov.html

3. Das Derivat

www.mathprofi.ru/chastnye_proizvodnye_primery.html

4. Gradient

mathprofi.ru /proizvodnaja_po_napravleniju_i_gradient.html

5. Gradientenabstieg

habr.com/de/post/471458

habr.com/de/post/307312

artemarakcheev.com//2017-12-31/linear_regression

6. NumPy library

docs.scipy.org/doc/ numpy-1.10.1 / reference / generate / numpy.linalg.solve.html

docs.scipy.org/doc/numpy-1.10.0/reference/generated/numpy.linalg.pinv.html

pythonworld.ru/numpy/2. html