Wir haben die Monte-Carlo-Methode untersucht . Heute werden wir sehen, wie der Computergeist im Jahr 2048 mit dem guten alten Minimax mit Alpha-Beta-Clipping spielt.

Der Artikel wurde mit Unterstützung von EDISON verfasst, einem Unternehmen, das mobile Anwendungen entwickelt und Software-Testdienste anbietet .
Vom Benutzer-Stackoverflow ausspionierte Lösung
 ovolve
ovolve , der in der Diskussion
feststellte ,
wie man AI das Spiel 2048 beibringt .
Kommentarübersetzung von ovolveIch bin der Autor des in diesem Thread erwähnten Programms. Sie können die KI
in Aktion sehen oder
den Code sehen .
Gegenwärtig gewinnt das Programm in etwa 90% der Fälle, indem es Java-Skripte in einem Browser auf meinem Laptop ausführt. Dabei werden 100 Millisekunden benötigt, um über den Kurs nachzudenken. Es funktioniert zwar nicht perfekt, aber ziemlich gut.
Da das Spiel ein diskreter Zustandsraum mit vollständigen Informationen ist und tatsächlich ein rundenbasiertes Spiel wie Schach und Dame ist, habe ich die gleichen Methoden verwendet, die ihre Leistung in diesen Spielen zeigten, nämlich die
Minimax-Suche mit
Alpha-Beta-Clipping . Da die Links viele Informationen zu diesem Algorithmus enthalten, werde ich nur auf die beiden wichtigsten Heuristiken eingehen, die ich in
der statischen Schätzfunktion verwendet habe, und viele der intuitiven Annahmen formalisieren, die andere Personen hier getroffen haben.

Monotonie
Diese Heuristik versucht sicherzustellen, dass alle Kachelwerte links / rechts und oben / unten entweder erhöht oder verringert werden. Diese Heuristik allein spiegelt die Vermutung wider, dass viele andere erwähnt haben, dass wertvollere Kacheln in einer Ecke gruppiert werden sollten. Dies verhindert in der Regel die Ansammlung von weniger wertvollen Kacheln und hält das Spielfeld organisiert, da kleinere Kacheln in größere übergehen.
Hier ist ein Screenshot eines komplett eintönigen Gitters. Ich habe diese Situation durch Ausführen eines Algorithmus mit der installierten Auswertungsfunktion erhalten, um andere Heuristiken zu ignorieren und nur Monotonie zu berücksichtigen.

Glätte (Glätte, Ebenheit)
Die obige Heuristik an sich neigt dazu, Strukturen zu erzeugen, in denen benachbarte Zellen an Wert verlieren, aber natürlich sollten Nachbarn die gleiche Bedeutung haben, um sie zu kombinieren. Daher misst die Heuristik der Glätte einfach die Wertdifferenz zwischen benachbarten Kacheln und versucht, deren Anzahl zu minimieren.
Ein Kommentator von Hacker News lieferte eine
interessante graphentheoretische
Formalisierung dieser Idee.
Übersetzung der Formalisierung mit Hacker NewsGestern habe ich dieses Spiel einem Kollegen gezeigt, einem Liebhaber der Graphentheorie, und wir haben uns auch entschlossen, darüber nachzudenken, wie wir dieses Spiel mit KI lösen können.
Die einfachste Lösung ist Minimax, die meiner Meinung nach ziemlich gut implementiert ist. Wenn jemand hier nicht mit minimax vertraut ist, hat OP sehr eleganten und gut kommentierten Code geschrieben, der ein großartiges Tutorial wäre.
Der weniger rechenintensive Ansatz, den wir vorgeschlagen haben, bestand darin, den Spielzustand in Form eines Graphen G (V, E) zu modellieren, wobei V eine Menge von aktiven Kacheln und E eine Menge von Kanten ist, die benachbarte Kacheln verbinden, gewichtet nach Funktion c (v1, v2) , die den absoluten Wert der Differenz zwischen den beiden Kacheln zurückgibt. Für jede Lösung wählt die KI einen Zug, der die Summe der Gewichte aller Kanten im neuen Spielzustand minimiert.
Der Grund dafür ist, dass der einzige Weg, um Fortschritte im Spiel zu erzielen, darin besteht, Kacheln mit denselben Werten nebeneinander zu haben, für die das Gewicht in G 0 beträgt. Daher sollte die KI versuchen, das Gesamtgewicht zu minimieren. Am Ende befindet sich eine große Anzahl an Brettern mit einem großen Gewicht an Kanten zu benachbarten Kacheln. Die KI wird daher versuchen, diese Kacheln neben anderen großen Kacheln zu belassen, um den Unterschied zu minimieren.
Da das Spiel stochastisch ist, funktioniert der von mir beschriebene Ansatz möglicherweise nicht im schlimmsten Fall, kann aber auch als Gewichtsfunktion für jeden Knoten im Baum auf die vorhandene Minimax-Lösung angewendet werden.
Hier ist ein Screenshot eines perfekt glatten Netzes, freundlicherweise zur Verfügung gestellt von dieser exzellenten
Scheingabel .
(Link zum Webarchiv, während Java-Skripte auf der Seite funktionieren und Sie die Tastatur verwenden können, um eine Bewegung in eine beliebige Richtung auszuführen - Anmerkung des Übersetzers).Lose Fliesen
Und schließlich gibt es eine Strafe für zu wenig freie Steine, da die Optionen schnell enden können, wenn das Spielfeld zu eng wird.
Und das ist alles! Das Durchsuchen des Spielraums bei gleichzeitiger Optimierung dieser Kriterien bietet eine überraschend gute Leistung. Einer der Vorteile eines solchen generischen Ansatzes anstelle einer explizit codierten Verschiebestrategie besteht darin, dass der Algorithmus häufig interessante und unerwartete Lösungen findet. Wenn Sie seinen Fortschritt beobachten, macht er oft erstaunliche, aber effektive Bewegungen, wie zum Beispiel den plötzlichen Wechsel von Wänden oder Ecken, in deren Nähe er sein Spiel baut.

Kleine Änderung
Der Screenshot zeigt die Leistungsfähigkeit dieses Ansatzes. Ich habe das Kachellimit entfernt (damit sie nach Erreichen von 2048 weiter wachsen), und hier ist das beste Ergebnis nach acht Tests.
Ja, das ist 4096 zusammen mit 2048. =) Dies bedeutet, dass er das schwer fassbare 2048-Plättchen auf einem Brett erreicht hat.
Java-Script-Code für minimax mit Alpha-Beta-Clipping und statischer Auswertungsfunktion aus dem Stackoverflow-User-Ovolve ist unten im Artikel angegeben.
Die Minimax-Methode ist mehreren ausgezeichneten Habr-Artikeln gewidmet, daher lassen wir die akademische detaillierte Erklärung dessen, woraus sie besteht, weg. Für diejenigen,
die erst kürzlich der IT-Community beigetreten sind, haben sie die schönen Begriffe "Minimax" und "Alpha-Beta-Cut-Off" gehört, aber sie wissen nicht, was dies bedeutet. Versuchen wir, in ein paar Absätzen buchstäblich die allgemeinste Bedeutung zu erklären.
Minimax
In einigen Spielen kann der Prozess eines Spiels zwischen zwei Spielern (die nacheinander einen Zug machen) als sogenannter Optionsbaum dargestellt werden. In jeder bestimmten Position hat jeder Spieler normalerweise die Wahl zwischen verschiedenen Optionen für seinen Zug. Und als Reaktion auf jede dieser Optionen kann ein Gegner auch in vielerlei Hinsicht ähnlich sein.
Fragment eines Baumes von OptionenDa zu jedem Zeitpunkt des Spiels vollständige Informationen über den Zustand des Spielfelds vorliegen, kann der aktuelle Zustand der Position immer genau geschätzt werden. Eine solche Funktion wird als
statische Bewertungsfunktion oder abgekürzter
SFO bezeichnet . Je wichtiger diese Funktion bei der Bewertung einer bestimmten Position ist, desto vorteilhafter ist außerdem die Position für einen Spieler (nennen wir sie den
maximierenden Spieler ). Je kleiner der numerische Wert dieser Funktion bei der Auswertung einer Position ist, desto vorteilhafter ist die Position für den zweiten Spieler (nennen wir es den
minimierenden Spieler ).
Nach jedem Zug ändert sich die Position und damit auch die Punktzahl. Bei der Betrachtung des Optionsbaums muss jeder Spieler nicht nur die Zweige bevorzugen, in denen die Bewertung für ihn am günstigsten ist. Sie sollten auch solche Zweige vermeiden, in denen die Bewertung der Position für den Gegner günstig ist.
Es wird davon ausgegangen, dass der Gegner sich auch von Rationalismus leiten lässt und auch Optionen vermeidet, die ihn zum Verlieren führen könnten. Das heißt, jeder Spieler maximiert bei der Auswahl einer Option seinen eigenen Nutzen und minimiert gleichzeitig den Gewinn des Gegners.
Das ist Minimax.
Alpha Beta Ausschnitt
Es liegt auf der Hand: Wer einen Baum von einer bestimmten Position bis zu einer größeren Tiefe berechnet, hat mehr Gewinnchancen. Aber es gibt ein Ärgernis: Der Baum der Optionen in Spielen hat die unangenehme Angewohnheit, sich mit jeder Verschachtelungsebene zu verzweigen und exponentiell zu wachsen. Die Zählfähigkeiten von Programmen und vor allem die der Menschen sind begrenzt, das Zählen "bis zur Matte" ist bei weitem nicht immer möglich. Es kann sich leicht herausstellen, dass der Spieler zu einer Position gezählt hat, bei der er eine gute Einschätzung des Spielfelds hat, aber auf der nächsten (unlesbaren) Ebene hat der Gegner buchstäblich die Möglichkeit, einen solchen Zug zu machen, der die Positionsschätzung grundlegend zum Gegenteil ändert.
Wer ist schuld und was zu tun? Der Rechenaufwand ist für die vollständige Durchquerung der Bäume verantwortlich, und es wird vorgeschlagen, unnötige Äste abzuschneiden, um zu kämpfen. Wenn der Spieler, der die Position bewertet, einen Zweig des Optionsbaums sieht:
oder weniger rentabel als andere Branchen, die bereits analysiert wurden,
oder vorteilhafter für den Gegner als andere Zweige, die bereits analysiert wurden,
dann wirft der Spieler diesen Zweig ab, verschwendet keine Zeit und Ressourcen damit, Unteroptionen aus diesem offensichtlich schlechteren Zweig für ihn in Betracht zu ziehen.
Auf diese Weise können Sie mehr Rechenressourcen für die Berechnung günstigerer Verzweigungen einer größeren Rendering-Tiefe im Optionsbaum zuweisen. Bei der Bewertung des Spielfelds auf verschiedenen Ebenen des Optionsbaums arbeitet der Spieler mit zwei sich dynamisch ändernden Koeffizienten -
Alpha (der Wert des SFD, der im Zweig minimal angetroffen wird - d. H. Für den minimierenden Spieler günstiger) und
Beta (der Wert des SFD, der im Zweig am häufigsten angetroffen wird - d. H. günstiger für den maximierenden Spieler). Wenn Sie die SFD der aktuellen Position mit den
Alpha und
Beta Koeffizienten vergleichen, können Sie auf jeder Ebene Zweige fegen (ohne sie vollständig zu berechnen), die für den Spieler, der die Position bewertet,
ungünstiger und / oder für seinen Gegner
vorteilhafter sind .
Dies ist Alpha-Beta-Clipping.
Rekursive Minimax-Funktion mit Alpha-Beta-Clipping
2048 mit AI ist als Excel-Anwendung mit VBA-Makros implementiert. So sieht der Minimax-Algorithmus mit Alpha-Beta-Clipping wie eine verabscheuungswürdige visuelle Basis aus. Ovolve Code in Java-Skript function AI(grid) { this.grid = grid; }
Statische Auswertungsfunktion
Da Sie auf jeder Ebene im Optionsbaum das Spielfeld bewerten müssen (um zu entscheiden, für welchen der Spieler die geschätzte Position tatsächlich vorteilhafter ist), müssen Sie entscheiden, welche Kriterien eine gute von einer schlechten Position unterscheiden.
Wir gehen davon aus, dass der maximierende Spieler die Person (oder KI) ist, die entscheidet, in welche der vier Richtungen (oben, links, rechts, unten) alle Steine verschoben werden. Ein minimierender Spieler ist diese heimtückische Unterroutine, die zufällig 2 oder 4 an den unangemessensten Stellen generiert.
SFO wird aus der Sicht eines maximierenden Spielers zusammengestellt. Je höher die SFD-Bewertung für das Spielfeld ist, desto besser ist die Position für den „Maximalisten“. Je niedriger - desto angenehmer ist die Position auf dem Brett für den "Minimalisten".
Im Fall von 2048 - welche Faktoren werden für denjenigen als günstig angesehen, der die Kacheln bewegt?
Monotonie
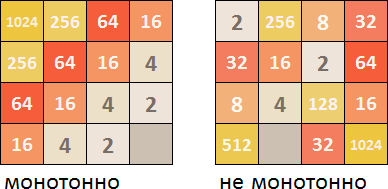
Erstens ist es wünschenswert, dass die Kacheln in aufsteigender / absteigender Reihenfolge in einigen Richtungen angeordnet sind. Wenn dies nicht erfolgt, wird das Spielfeld beim Generieren neuer Kacheln schnell durch zufällig angeordnete Kacheln unterschiedlicher Größe verstopft, die nicht sofort normal miteinander verbunden werden können.
Im Sibirischen Bundesdistrikt müssen Sie in alle vier Richtungen schauen (von oben nach unten, von links nach rechts, von rechts nach links, von unten nach oben) und berechnen, wo die Kacheln eine abnehmende oder zunehmende Progression aufweisen. Wenn es im Laufe der Zeit Kacheln gibt, die nicht in die allgemeine Reihe passen, verringert dies den numerischen Monotoniekoeffizienten. Dann wird aus den 4 Koeffizienten für alle Richtungen der beste ausgewählt, der im Gesamtwert des Sibirischen Bundesdistrikts berücksichtigt wird.
Glätte

Darüber hinaus wäre es vorzuziehen, wenn der Fortschritt vom Stehen in einer Reihe von Kacheln nicht nur zunimmt, sondern nicht abnimmt (oder statt der Reihe zu verringern, ist es vorzuziehen, nicht zuzunehmen), das heißt, es ist gut, wenn dieselben Kacheln in der Nähe sind, was es ihnen ermöglicht, zu einer zusammenzufallen, Punkte zu gewinnen und Erhöhung des freien Platzes auf dem Spielfeld.
Daher sucht der Sibirische Bundesdistrikt auf dem Spielfeld nach denselben benachbarten Kacheln und berücksichtigt die Anzahl solcher Paare in einem speziellen Koeffizienten.
Leere Zellen

Je mehr Freiraum vorhanden ist, desto mehr Spielraum ist vorhanden und desto geringer ist die Wahrscheinlichkeit, schnell zu verlieren.
SFO betrachtet leere Zellen auf dem Spielfeld und je mehr davon, desto profitabler wird die Position für den maximierenden Spieler.
Maximale Kachel
Da die Hauptsache in diesem Spiel darin besteht, ein großes Plättchen auf das Spielfeld zu bringen, sollten die Optionen, bei denen der maximale Plättchenwert höher ist, als das rentabelste SFD angesehen werden, je mehr desto besser - 2048, 4096, 8192 (oder was auch immer Sie die Stärke und Geduld dafür haben).
Sibirischer Bundesdistrikt für 2048
Implementierung des Sibirischen Bundesdistrikts als VBA-Makro Ovolve-Code im Java-Skript function Grid(size) { this.size = size; this.startTiles = 2; this.cells = []; this.build(); this.playerTurn = true; }
2048.xlsm
Die Excel-Anwendung selbst
kann von Google heruntergeladen werden .
Die Funktionalität der Anwendung wurde
in einem früheren Artikel beschrieben, in dem AI nach der Monte-Carlo-Methode spielt . Die heutige Lösung wurde dem bestehenden Monte Carlo hinzugefügt.
Alle Artikel der AI- und 2048-Serie
- Monte Carlo
- Minimax + Alpha-Beta-Ausschnitt
- Warten auf Maximum
- Neuronales Netz