TextRadar Fuzzy Search Algorithmus - Grundlegende Ansätze
Im Gegensatz zu Fuzzy-String-Vergleichen werden bei gleichwertigen Vergleichszeichenfolgen die Suchzeichenfolge und die Datenzeichenfolge in der Fuzzy-Suchaufgabe hervorgehoben, und es muss nicht der Ähnlichkeitsgrad der beiden Zeichenfolgen bestimmt werden, sondern der Grad der Präsenz der Suchzeichenfolge in der Datenzeichenfolge.
Erklärung des Problems
Eine Daten- und eine Suchzeichenfolge werden als beliebige Zeichensätze angegeben, die aus Wörtern bestehen - durch Leerzeichen getrennte Zeichengruppen.
Es ist erforderlich, in der Datenzeile den Satz von Fragmenten zu finden, der der Suchzeile durch die Zusammensetzung und die relative Position der Zeichen am nächsten liegt.
Berechnen Sie zur Beurteilung der Qualität des Suchergebnisses den Relevanzkoeffizienten, dessen Wert im Bereich von 0 bis 1 liegen soll, wobei 0 der vollständigen Abwesenheit von Zeichen des Suchstrings im Datenstring und 1 der Anwesenheit des Suchstrings im Datenstring in unverzerrter Form entsprechen soll.
Die Suche sollte durch zeichenweise Analyse der Quellzeilen unter Berücksichtigung der gegenseitigen Anordnung von Zeichen und Wörtern in den Zeilen erfolgen, ohne jedoch die Syntax und Morphologie der Sprache zu berücksichtigen.
Beschreibung des Algorithmus
Die Suche erfolgt in mehreren Schritten.
Konstruktion einer Zufallsmatrix
Die Übereinstimmungsmatrix (M) ist eine zweidimensionale Matrix, deren Anzahl Spalten der Länge der Datenzeichenfolge und deren Anzahl Zeilen der Länge der Suchzeichenfolge entspricht. Die Elemente der Koinzidenzmatrix nehmen Werte 0 oder 1 an, je nachdem, ob die entsprechenden Zeichen der Linien übereinstimmen oder nicht, mit Ausnahme von Leerzeichen (Worttrennzeichen).
Die Übereinstimmungsmatrix für die Datenzeichenfolge "ABCD EF" und die Suchzeichenfolge "ABC" hat die Form:
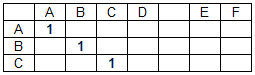
Übereinstimmungsmatrixelement m (i, j) = 1, wenn d (i) = s (j), wobei D ein Array von Datenzeichenfolgenzeichen ist, S ein Array von Suchzeichenfolgenzeichen ist, i eine Spaltennummer der Übereinstimmungsmatrix M (Zeichennummer einer Datenzeichenfolge) ist ), j ist die Zeilennummer der Übereinstimmungsmatrix (die Nummer des Zeichens in der Suchzeichenfolge). In anderen Fällen ist m (i, j) = 0. Übereinstimmungen von Worttrennzeichen (in unserem Fall Leerzeichen) werden nicht berücksichtigt, das heißt: m (i, j) = 0, wenn d (i) = s (j) = '' .
Passen Sie die Matrixdiagonalen an
Elemente der Koinzidenzmatrix M bilden Diagonalen. Elemente der Matrix befinden sich auf derselben Diagonale, wenn sich ihre Indizes i und j gleichzeitig um +1 oder um - 1 unterscheiden.

Diagonalen entsprechen den Positionen des Suchstrings in der Reihenfolge der Offsets entlang des Datenstrings.

Elemente einer der Diagonalen und die entsprechende Verschiebung in der obigen Abbildung sind blau hervorgehoben.
Die Idee, bei einem Fuzzy-Suchproblem eine Folge von Linienverschiebungen relativ zueinander zu verwenden, geht auf die bekannte Technik zur Erfassung von Radarsignalen vor einem Interferenzhintergrund zurück, bei der die gegenseitige Korrelationsfunktion von Funksignalen berechnet wird. Die Kreuzkorrelationsfunktion bestimmt den Ähnlichkeitsgrad der um die Zeit τ gegeneinander verschobenen Kopien zweier verschiedener Signale v (t) und u (t) und wird als Integral definiert: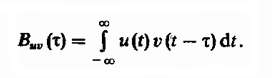
Die Gesamtzahl der Diagonalen wird nach folgender Formel berechnet:

Die Längen der Diagonalen entsprechen der Länge der Suchzeichenfolge.
Gruppen zuordnen
Aufeinanderfolgende Einheiten in den Diagonalen der Koinzidenzmatrix bilden Gruppen von Übereinstimmungen. Unten finden Sie Übereinstimmungsgruppen für die Datenzeichenfolge "ABCD DEF JH" und die Suchzeichenfolge "ABC DE J" - 4 Gruppen, die sich auf verschiedenen Diagonalen befinden.

Projektionsmatrizen
Die Diagonalen der Übereinstimmungsmatrix und die darin enthaltenen Übereinstimmungsgruppen werden den entsprechenden Abschnitten der Suchzeichenfolge und der Datenzeichenfolge zugeordnet und bilden zwei Projektionsmatrizen - die Suchzeichenfolge bzw. die Datenzeichenfolge. In unserem Beispiel sehen Projektionsmatrizen folgendermaßen aus:
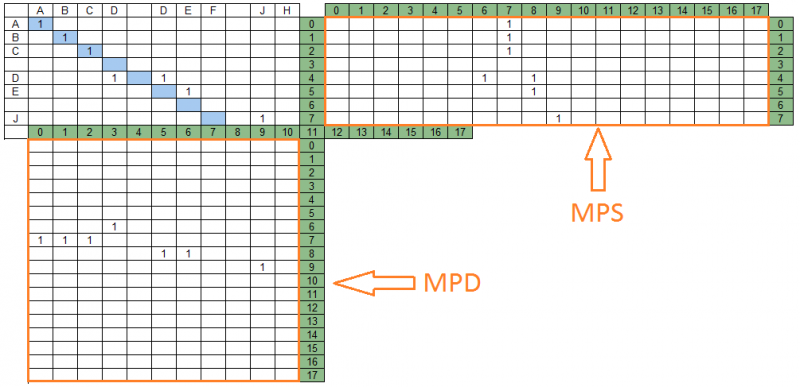
In der obigen Abbildung befindet sich rechts neben der Übereinstimmungsmatrix die Matrix der Projektionen auf die Suchzeichenfolge - MPS, unten - die Matrix der Projektionen auf die MPD-Datenzeichenfolge. Die Anzahl der MPS-Spalten entspricht der Anzahl der MPD-Zeilen und der Anzahl der Diagonalen der Übereinstimmungsmatrix - in unserem Beispiel sind es 18.
Suchen Sie nach einer Ergebnismenge von Gruppen
Um das Problem zu lösen, ist es notwendig, eine solche Gruppe von Gruppen zu finden, die den Suchstring mit der geringsten Fragmentierung (so groß wie möglich) ohne gegenseitige Überschneidungen in den Projektionsmatrizen am besten "abdeckt" und deren Zuordnung zum Datenstring dem "Original" -Suchstring am nächsten kommt .
Schnittpunkt von Gruppen in der ProjektionsmatrixIn unserem Beispiel gibt es Gruppen, die sich in der MPS-Matrix überschneiden. In der folgenden Abbildung sind sie rot hervorgehoben. Darüber hinaus schneiden sich in der MPD-Matrix dieselben Gruppen nicht, in der Abbildung sind sie grün hervorgehoben.
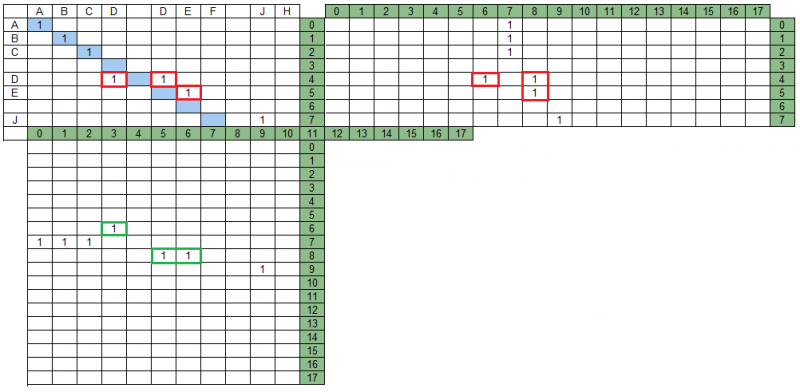
Die Suche nach der resultierenden Gruppe von Gruppen impliziert, dass nicht alle Gruppen darin enthalten sind und dass einige der verbleibenden Gruppen geändert (abgeschnitten) werden können, wenn gegenseitige Schnittpunkte von Gruppen in Projektionen analysiert werden.
Die Suche nach der Ergebnismenge kann durchgeführt werden, indem der "unendliche" Zyklus (die Anzahl der Iterationen des Zyklus überschreitet nicht die Anzahl der Gruppen) der
Tabelle aller Gruppen durchlaufen wird, in die Gruppen der Übereinstimmungsmatrix anfänglich eingefügt werden, wobei bei jeder Iteration die folgenden Aktionen ausgeführt werden:
- Auswahl der besten anhand bestimmter Parameter (abhängig vom Kontext des zu lösenden Problems) - im einfachsten Fall kann dies die Wahl der ersten Gruppe der größten Größe sein, die auftritt;
- Platzierung der besten Gruppe in der Tabelle der Ergebnisgruppen und deren Entfernung aus der Tabelle aller Gruppen (deren Zeilen gecrawlt werden);
- Entfernen (oder Abschneiden) von Gruppen, die sich mit der ausgewählten besten Gruppe in den Projektionsmatrizen von Gruppen überschneiden, aus der Tabelle.
Die optimale Gruppe von Gruppen für unser Beispiel ist in der folgenden Abbildung dargestellt - Gruppengruppen sind orange hervorgehoben.

Die während der Schnittpunktverarbeitung gelöschte Gruppe (Schnittpunkt in der MPS-Matrix mit der besten Gruppe der zweiten Iteration) wird rot hervorgehoben.
Das Suchergebnis in der Datenzeile sieht folgendermaßen aus:

Berechnung des Relevanzkoeffizienten
Zur quantitativen Bewertung der Suchergebnisse werden die Längen der gefundenen Gruppen mit den Wortlängen des Suchstrings (Gruppenzusammensetzungsbewertung) sowie die Gesamtlänge des Suchstrings mit der Länge der gefundenen Gruppen im Datenstring verglichen. Es wird angenommen, dass die Bedeutung der Bewertung der Zusammensetzung der gefundenen Gruppen höher ist als die Bedeutung der Ausmaßschätzung in der Datenzeile, die in den Gewichtungskoeffizienten der Formel zur Berechnung des Relevanzkoeffizienten berücksichtigt wird:

Wenn der Gruppenzusammensetzungskoeffizient als Verhältnis der Summe der quadratischen Längen der gefundenen Gruppen zur Summe der quadratischen Längen der Wörter der Suchzeichenfolge berechnet wird:

Der Längenfaktor ist das Verhältnis der Länge der Suchzeichenfolge zur Gesamtlänge der gefundenen Gruppen in der Datenzeichenfolge. Wenn der auf diese Weise erhaltene Wert größer als 1 ist, wird sein inverser Wert genommen:

Für unser Beispiel:

Geschätzter Umfang der Datenverarbeitung
Die ressourcenintensivsten Vorgänge sind:
- Bestimmung der Übereinstimmungsmatrix M - Die Anzahl der Matrixelemente ist definiert als das Produkt der Länge der Suchzeichenfolge durch die Länge der Datenzeichenfolge: L * L;
- Definition von Projektionsmatrizen auf Daten und Suchstrings - Die Anzahl der Matrixelemente ist für MPS: (L + L - 1) * L, für MPD: (L + L - 1) * ;
- die Bildung der Tabelle aller Gruppen - die Anzahl der Gruppen wird den Wert L * L / 2 nicht überschreiten;
- Suche nach der resultierenden Gruppe von Gruppen - Die Anzahl der Iterationen des Zyklus überschreitet nicht die anfängliche Anzahl von Gruppen, dh L * L / 2.
Somit ist die Gesamtmenge der Berechnungen ein Vielfaches des Produkts der Länge der Suchzeichenfolge mit der Länge der Datenzeichenfolge:

Die Linearität des Rechenaufwands im Verhältnis zur Größe der Quelldaten ist ein wichtiges Argument für die praktische Anwendung des Algorithmus.
Nichtlinearität
Es ist anzumerken, dass die Linearität auf einem vereinfachten Verfahren zum Auffinden der resultierenden Gruppe von Gruppen beruht. Wenn wir im allgemeinen Fall alle möglichen Optionen zum Platzieren von Gruppen in einer Datenzeile berücksichtigen, mögliche Schnittpunktverarbeitungsoptionen berücksichtigen und den besten
Satz von Gruppen aus dem Satz möglicher auswählen, anstatt bei jeder Iteration des Zyklus
eine Gruppe auszuwählen, ist die Anzahl der Berechnungen in Bezug auf die Größe nicht mehr linear Quelldaten. Die nichtlineare Abhängigkeit des Rechenaufwands von der Größe der Quelldaten schränkt die Möglichkeiten der praktischen Anwendung stark ein.
Finde das Gleichgewicht
Um ein optimales Gleichgewicht zwischen der Qualität der Suche und dem Bedarf an Ressourcen zu gewährleisten, ist es wichtig, die richtige Suchmethode für die resultierende Gruppe von Gruppen zu wählen. Dies kann in der Regel mithilfe der Kontextmerkmale des zu lösenden Problems erfolgen.
Auf der Website
textradar.ru wurde ein Demo-Stand bereitgestellt, auf dem Sie die Funktionsweise des Algorithmus testen können.
Vergleich mit Analoga:
Vergleich des TextRadar-Fuzzy-Suchalgorithmus mit Analoga: Lucene, Sphinx, Yandex, 1C