Eine der schwierigsten Aufgaben in computergestützten Konstruktionssystemen ist das Filetieren beim Modellieren von Objekten komplexer Formen. Für die Konstruktion von Rundungen sowie für die gesamte Geometrie im CAD ist der geometrische Kern verantwortlich.

Aus Sicht des Kernel-Entwicklers ist es aufgrund ihrer unendlichen Vielfalt unmöglich, alle Rundungsmöglichkeiten abzudecken. Unsere Mathematiker fügen dem C3D-Kern ständig neue Sonderfälle hinzu und haben kürzlich eine Rundung von drei Gesichtern (oder eine vollständige Rundung) durchgeführt.

Was ist seine Komplexität und wie funktioniert der Algorithmus, sagt Anna Ladilova, Mathematikerin und Programmiererin bei C3D Labs.

Was ist Vollrundung?

Angenommen, wir haben einen Körper mit drei Gesichterketten - zentral (oben) und seitlich (rechts und links). Es ist erforderlich, die Mittelfläche durch eine Verrundungsfläche zu ersetzen, die problemlos in benachbarte Seitenflächen passt. Diese neue Oberfläche wird vollständig abgerundet sein. Im Allgemeinen hat es einen variablen Radius, der automatisch erkannt wird.



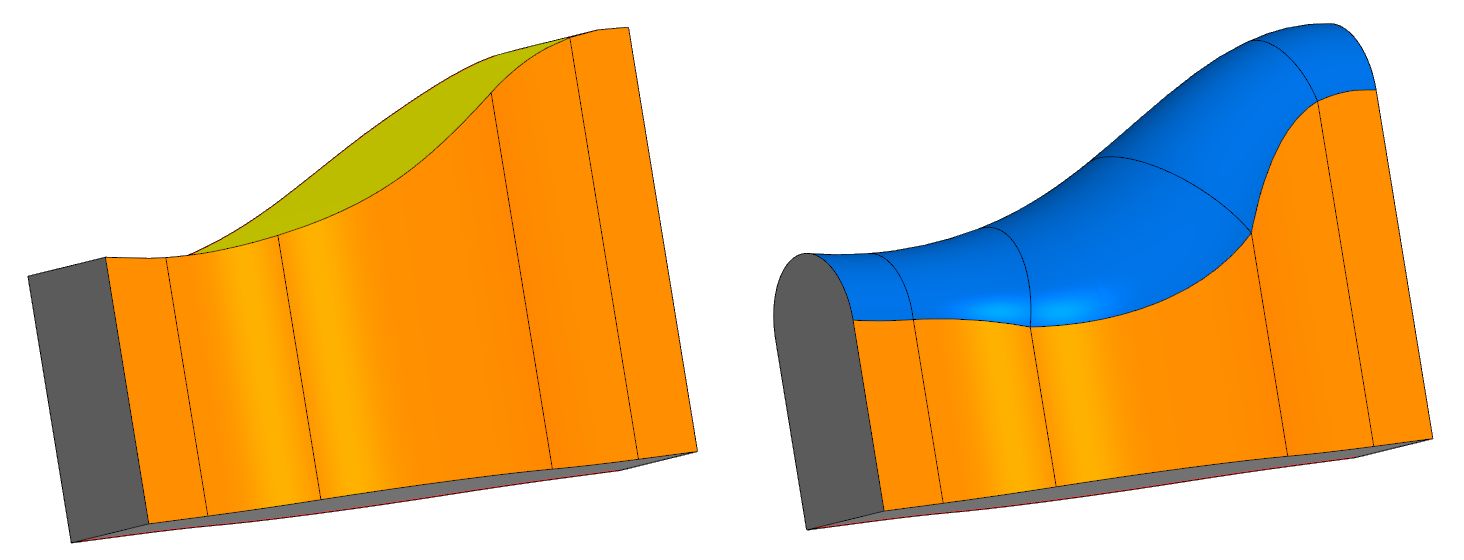
In vielen bekannten CAD-Systemen ist die Vollrundungsverrundungsoperation implementiert, ihre Mathematik wird jedoch nicht offenbart.


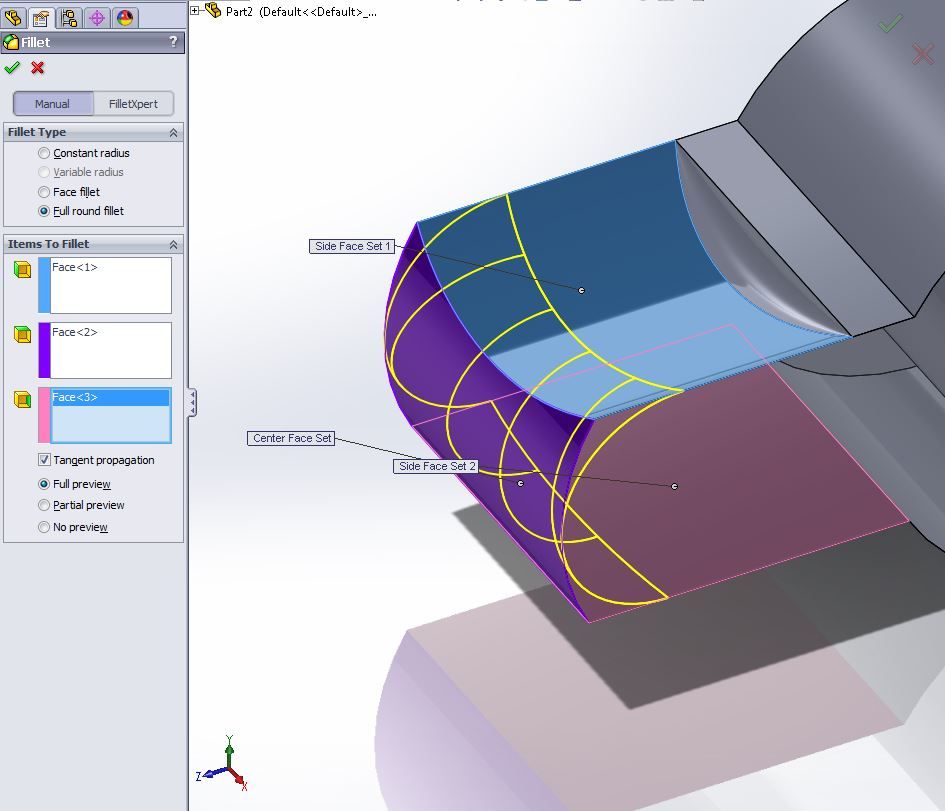Solidworks Vollrundfiletbetrieb

Deshalb haben wir unseren eigenen Algorithmus entwickelt. Und es unterscheidet sich von den Algorithmen anderer Entwickler.

Operationen, obwohl sie als gleich bezeichnet werden, führen zu leicht unterschiedlichen Ergebnissen. Dies legt nahe, dass SolidWorks eine andere Definition für das Runden von drei Flächen bietet.


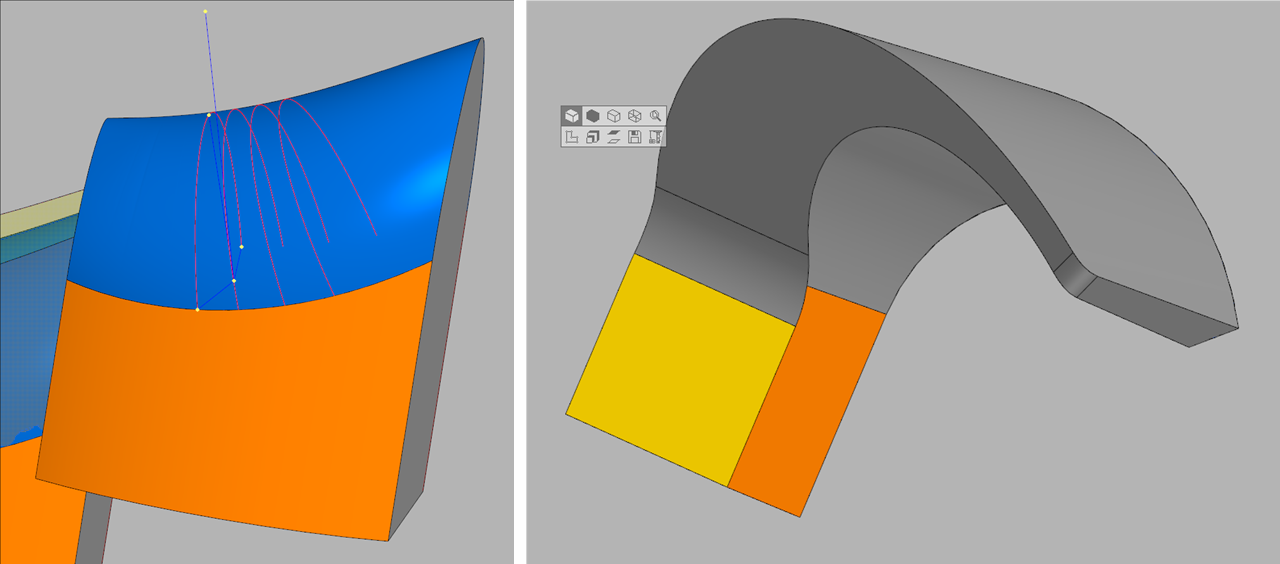
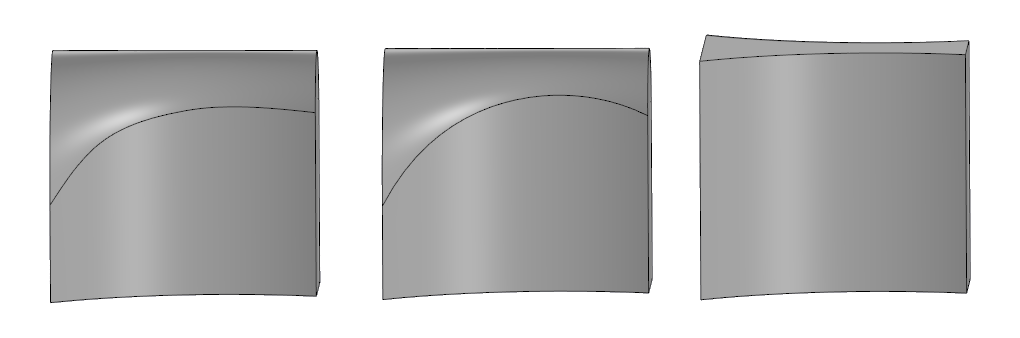Rechts das Originalmodell, in der Mitte die vollständige Rundung in SolidWorks, links die C3D.

Vollständiger Rundungsalgorithmus

Das Erstellen von Filets jeder Art umfasst mehrere Phasen:

1. Brechen Sie die angegebene Kette in elementare Komponenten (zum Abrunden von drei Flächen sind es genau drei Flächen: links, rechts und mittig).
2. Ordnen Sie konsequent elementare Komponenten an.
3. Erstellen Sie für jede Elementarkomponente eine Verrundungsfläche.
4. Nähen Sie benachbarte Filetflächen mit Rippen.
5. Um die Endabschnitte der Filetkette zu verarbeiten, d. H. Sie korrekt mit dem modifizierten Körper zu verbinden.

Der entscheidende Punkt bei diesem Verfahren ist der dritte Schritt: Erstellen einer Verrundungsfläche für drei vorgegebene Flächen.

Um die gewünschte Oberfläche zu konstruieren, müssen zunächst die Kurven bestimmt werden, mit denen die Verrundung jede der drei Flächen berührt. Im allgemeinen Fall können diese Kurven nur als Splines konstruiert werden, die durch bekannte Punkte verlaufen, die im Voraus berechnet wurden.

Überlegen Sie, wie Sie ein Tripel von Punkten berechnen können - einen auf jedem Spline.


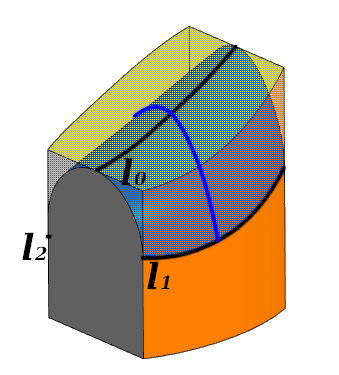Elementarverarbeitung. Das Filet berührt jede der drei Flächen entlang der Kurven l ₀ ; l ₁ ; l ₂ . Die blaue Linie zeigt den Querschnitt

In jedem Querschnitt $$$ABC$:

• $$$OA = OB = OC$- automatisch berechnet
• $$$OA, OB, OC$orthogonal zu den Tangentialebenen der Flächen an den entsprechenden Punkten
• $$$p$₀ - Ankerpunkt, liegt in der Ebene $$$ABC$.

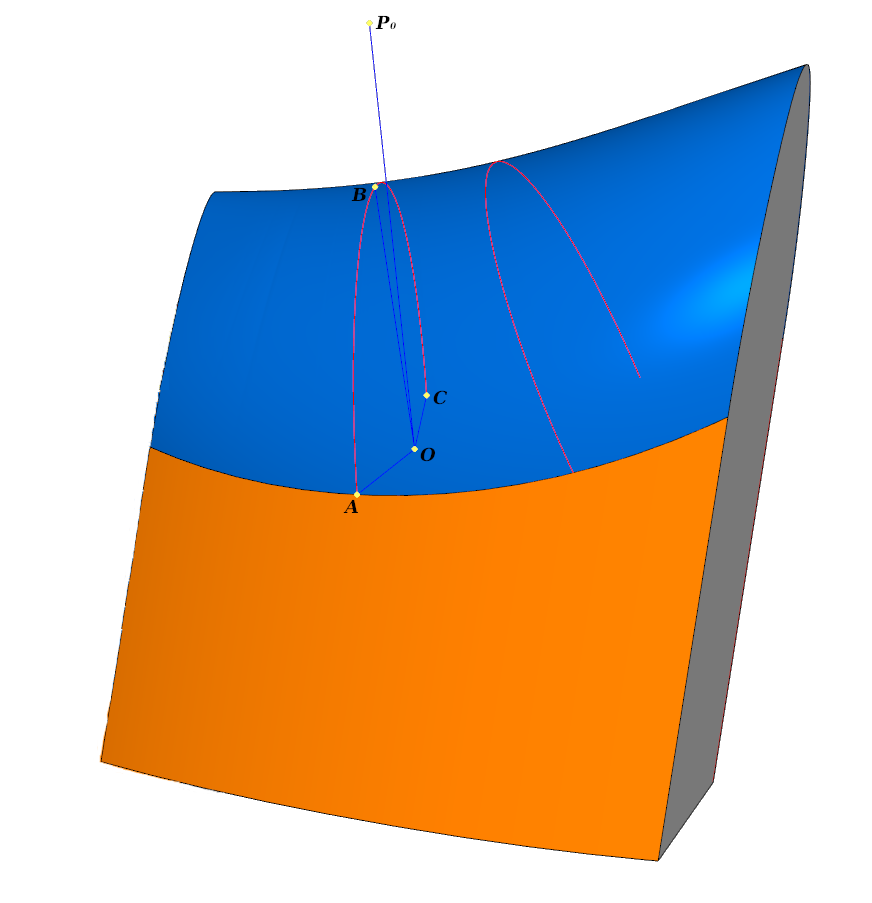
Wir definieren die Anfangsflächen der mittleren, linken und rechten Fläche durch Radiusvektoren in einem bestimmten Definitionsbereich. Die Seitenflächen seien durch Radiusvektoren definiert $$$r$₁ $$$(u, v)$und $$$r$₂ $$$(z, w)$und der zentrale $$$r$₀ $$$(x, y)$. Wir führen einen positiven numerischen Parameter ein $$$d$.

Bezeichnen mit $$$n$₀ $$$(x, y)$, $$$n$₁ $$$(u, v)$, $$$n$₂ $$$(z, w)$einzelne Normalen zu den entsprechenden Flächen, gerichtet "nach innen".


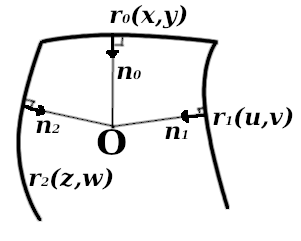Querschnitt beim Erstellen einer Verrundung

Wir fordern, dass sich die Enden dieser Normalen erstrecken $$$d$Mal einen Punkt treffen - Punkt $$$O$.

In Bezug auf die Differentialgeometrie können unsere Anforderungen durch ein System von sieben Gleichungen mit sieben Parametern formuliert werden:

$$$dn$₀ $$$(x, y)$= $$$dn$₁ $$$(u, v)$,
$$$dn$₀ $$$(x, y)$= $$$dn$₂ $$$(z, w)$,
( $$$r$₀ $$$(x, y)$- $$$p$₀ $$$r$₁ $$$(u, v)$- $$$p$₀ $$$r$₂ $$$(z, w)$- $$$p$₀ ) = $$$0$,

wo

• $$$d$- variabler Radius
• $$$p$₀ - Ankerpunkt
• $$$x, y, u, v, z, w$- Variablen aus dem Parameterdefinitionsbereich.

Mit Algorithmen numerischer Methoden (zum Beispiel Newtons Methode) finden wir eine Lösung für dieses System: $$$x$₀ $$$y$₀ $$$u$₀ $$$v$₀ $$$z$₀ $$$w$₀ $$$d$₀ .

Die Lösung definiert Berührungspunkte mit Oberflächen:

• $$$r$₀ ( $$$x$₀ $$$y$₀ )
• $$$r$₁ ( $$$u$₀ $$$v$₀ )
• $$$r$₂ ( $$$z$₀ $$$w$₀ )

sowie Radius $$$d$₀ .

Laufen durch eine Reihe von Punkten $$$p$₀ , wir erhalten Dreiergruppen von Tangentenpunkten mit Flächen, von denen aus Sie „Berührungskurven“ wiederherstellen können. $$$l$₀ $$$l$₁ $$$l$₂ als Hermite Splines durch berechnete Punkte.

Geltungsbereich [ $$$t$_min $$$t$_max ] alle Kurven sind gleich und der Parameter $$$t$_Ich korrespondiere mit einem Punkt $$$r$_0i $$$r$_1i $$$r$_2i . Ferner werden diese Kurven verwendet, um den gewünschten Verrundungsquerschnitt zu berechnen.

Wir korrigieren einige Parameter $$$t$und berechne die Punkte dafür:

• $$$r$₀ $$$(x (t), y (t)),$
• $$$r$₁ $$$(u (t), v (t)),$
• $$$r$₂ $$$(z (t), w (t))$.

Wir konstruieren eine Spline-Kurve, die durch diese Punkte und senkrecht dazu stehenden Normalenvektoren verläuft $$$n$₀ $$$(x (t), y (t))$, $$$n$₁ $$$(u (t), v (t))$, $$$n$₂ $$$(z (t), w (t))$dementsprechend.

Wenn die Problemstellung geringfügig geändert wird und die Kurve an bestimmten Punkten und Tangentenvektoren an diesen Punkten gesucht wird, finden Sie die Methoden, mit denen ein solcher Spline implementiert werden kann, beispielsweise in Nikolai Golovanovs Buch „Geometric Modeling“.

Das Buch beschreibt detailliert die Methoden zum Abrunden der Körperkanten, insbesondere wird gezeigt, dass der Querschnitt der Rundung als NURBS-Kurve realisiert werden kann, die durch drei Punkte definiert ist. Wenn drei Flächen gerundet sind, wird eine ähnliche Kurve durch fünf Punkte bestimmt.

Also für jeden Parameter $$$t$Wir können eine Reihe von Punkten für die Konstruktion von NURBS definieren und daher jeden Punkt des Querschnitts der Verrundungsoberfläche definieren. Damit ist das Problem der Oberflächenkonstruktion vollständig gelöst.

In der Beschreibung dieses Teils des Algorithmus gab es eine kleine Frage: Wie wählt man die Punktmenge „richtig“ aus? $$$p$₀ entspricht dem Querschnitt, durch den die „Berührungskurven“ leicht wiederhergestellt werden können $$$l$₀ $$$l$₁ $$$l$₂ ?

Es erscheint vernünftig, sie mit einer vorgewählten Kurve zu nehmen. Wir werden nicht auf die Details der Konstruktion dieser Kurve eingehen, sondern nur darauf achten, dass sie glatt sein sollte, ohne Selbstüberschneidungen und die Kantenketten, die die Mittelfläche links und rechts begrenzen, „mitteln“.


Links, Querschnitt, punktabhängig $$$p$₀ .
Auf der rechten Seite können die Zahlen sehr komplex sein, daher ist die richtige Auswahl der „Hilfskurve“ eine separate Aufgabe.

Nachdem wir nun in der Lage sind, Verrundungsflächen für die einfachsten Elementarfälle zu erstellen, können wir uns einem komplexeren Problem zuwenden: der Erstellung einer Fläche für eine Kette von Flächen.
Das Hauptproblem besteht darin, benachbarte Flächen glatt zu „nähen“. Dies ist der vierte Schritt des Algorithmus.

Die Schwierigkeit liegt genau in der Glätte der Vernetzung, da die Oberflächen mit unterschiedlichen Anfangsdaten aufgebaut sind. Um die Glätte zu gewährleisten, muss man auf verschiedene Tricks zurückgreifen: Ändern Sie die Richtung und Länge der Vektoren von Ableitungen in Längsrichtung in einem bestimmten Abstand von der Grenze, ändern Sie die Werte der Ableitungen von Gewichtsfunktionen an den Grenzen usw. Die Ergebnisse sind in der Abbildung sichtbar: Die glatteren Zebra-Linien entsprechen einer glatteren Oberfläche.




Oben ist ein Modell ohne Glättungsalgorithmus dargestellt. Unten - nach Anwendung des Algorithmus.

Zusammenfassung

Als Ergebnis unserer Forschung ist der geometrische C3D-Kern in der Lage, einen Verrundungsquerschnitt, Stützkurven und Verrundungen von drei Flächen zu konstruieren. weiß, wie die Oberfläche durch Auswahl einer Parametrisierung geglättet wird; weiß teilweise, wie benachbarte Verrundungsflächen reibungslos verbunden werden können.


Autorin - Anna Ladilova, Ph.D., Mathematikerin / Programmiererin C3D Labs