Funktionsweise der Kryptographie mit elliptischen Kurven in TLS 1.3

Einige Leserbenachrichtigungen:

Um den Beschreibungsprozess (etwas) zu vereinfachen und das Volumen des Artikels, den wir schreiben werden, zu verringern, ist es wichtig, sofort eine wichtige Bemerkung zu machen und die Hauptbeschränkung anzugeben - alles, was wir Ihnen heute zum Praktischen sagen werden Seite der Problematik ist nur in Bezug auf TLS 1.3 realisierbar. Das bedeutet, dass Ihr ECDSA-Zertifikat zwar weiterhin in TLS 1.2 funktioniert, wenn Sie dies wünschen, jedoch Abwärtskompatibilität bietet. Die Beschreibung des tatsächlichen Handshake-Prozesses, der Verschlüsselungsverfahren und der Client-Server-Benchmarks bezieht sich jedoch nur auf TLS 1.3. Dies bezieht sich natürlich nicht auf die mathematische Beschreibung von Algorithmen hinter modernen Verschlüsselungssystemen.

Dieser Artikel wurde weder von einem Mathematiker noch von einem Ingenieur verfasst - obwohl diese dabei halfen, einen Weg um die gruselige Mathematik zu finden, und diesen Artikel rezensierten. Vielen Dank an die Mitarbeiter von Qrator Labs.

( E lliptic C urve) D iffie- H ellman ( E phemeral)

Das Diffie-Hellman-Erbe im 21. Jahrhundert

Natürlich hat dies weder mit Diffie noch mit Hellman begonnen. Um jedoch eine korrekte Zeitachse bereitzustellen, müssen wir auf die wichtigsten Daten und Ereignisse hinweisen.

Bei der Entwicklung der modernen Kryptographie gab es mehrere bedeutende Persönlichkeiten. Vor allem Alan Turing und Claud Shannon haben beide unglaublich viel Arbeit auf dem Gebiet der Rechnungs- und Informationstheorie sowie der allgemeinen Kryptoanalyse geleistet, und sowohl Diffie als auch Hellman wurden offiziell die Idee des öffentlichen Schlüssels zugeschrieben (oder sogenannte asymmetrische) Kryptographie (obwohl bekannt ist, dass es in Großbritannien ernsthafte Fortschritte in der Kryptographie gab, die sehr lange im Verborgenen blieben), die diese beiden Herren zu Pionieren machten.

In was genau?

Nun, das mag merkwürdig klingen. Vor dem 6. November 1976 gab es jedoch keine öffentlichen Kenntnisse über Verschlüsselungssysteme mit öffentlichem Schlüssel. Whitfield Diffie und Martin Hellman (und tatsächlich Ralph Merkle) - Mathematiker, Computeringenieure und Enthusiasten sowie Kryptologen waren die ersten.

Für diejenigen, die sich nicht bewusst sind - aufgrund der Rolle, die die Kryptoanalyse während des Zweiten Weltkriegs einnahm, und ihrer enormen Auswirkung auf die Geheimhaltung von Informationen -, haben die beiden Länder, die sie für am weitesten fortgeschritten hielten, die Verschlüsselung in ihre Munitionslisten aufgenommen und genutzt ein starkes Exportverbot (das gleichzeitig die Implementierung der Verschlüsselung für den privaten und gewerblichen Gebrauch im Inland schwächt). Aus diesem Grund wurden die britischen Forscher, die im Government Communications Headquarters an der Technik des Austauschs asymmetrischer Schlüssel arbeiteten und ein analoges Schema entwickelten, für diese Erfindung erst 1997 anerkannt, als Beschränkungen für Kryptografiealgorithmen und deren Beschreibung unwirksam wurden.

Zurück zu unseren beiden Erfindern - was haben Diffie und Hellman konkret revolutioniert?

Werfen wir einen Blick auf ihre Originalarbeit und veranschaulichen den großen Sprung, den sie eingeführt haben (sogar theoretisch mit ihrer Forschungsarbeit):

Und der folgende:

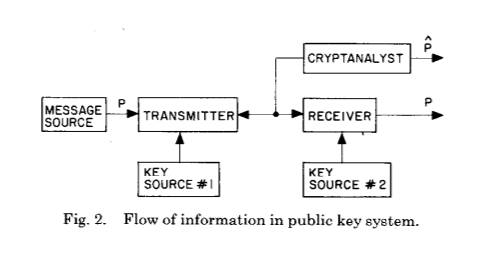
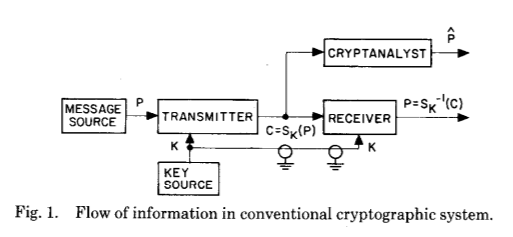
Diese beiden Bilder veranschaulichen perfekt die enorme Veränderung, die Whitfield Diffie und Martin Hellman nach der Kryptographie und Kryptoanalyse in Jahrhunderten der Evolution eingeführt haben - die Etablierung eines gemeinsamen geheimen Schlüssels als Ergebnis einer kryptographischen Berechnung.

Schauen wir uns ein weiteres gutes Bild mit Farben an:



Es erklärt, was los ist. Vor der Erfindung der Diffie- und Hellman-Schlüsselvereinbarung gab es nur einen symmetrischen Schlüssel - er wurde sowohl zum Ver- als auch zum Entschlüsseln der Nachricht verwendet. Wenn Sie jemandem einen solchen „Schlüssel“ geben möchten, muss dieser über einen „sicheren“ Kanal übertragen werden. Sie können sich sofort alle Einschränkungen eines solchen Schemas der vorherigen Generation vorstellen - Sie benötigen einen bereits eingerichteten sicheren Kanal, können den Schlüssel nicht wiederverwenden , und im Idealfall sollte die Länge des Schlüssels der Länge der Nachricht entsprechen.

Claude Shannon hat in seiner in der Kriegszeit klassifizierten Arbeit " Communication Theory of Secrecy Systems " bewiesen, dass alle theoretisch unzerbrechlichen Chiffren die gleichen Anforderungen erfüllen müssen wie die einmalige Unterlage - bekannt als Vernam-Chiffre - vom Autor dieser symmetrischen polyalphabetischen Stream-Chiffre.

Wir werden uns noch einmal das Originalpapier ansehen:


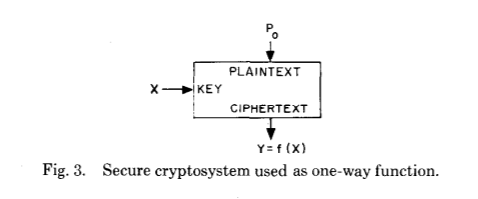
Bevor wir weitermachen, fragen wir uns, wie zwei, wenn auch brillante, Menschen auf einem angewandten Gebiet mit einer solchen Geschichte, insbesondere zur Zeit des Krieges, zu einer so signifikanten Verbesserung gekommen sind.
Nun, wegen der:

• Informationstheorie , formuliert von Claude Shannon;
• Berechnungstheorie , die insbesondere von Alonzo Church, John von Neumann und Alan Turing beeinflusst wird;
• Und, was noch wichtiger ist, die Berechenbarkeitstheorie basiert hauptsächlich auf Turings Arbeiten, die wir alle zur gleichen Zeit des 20. Jahrhunderts entwickelt und gereift haben. Diffie und Hellman nannten beide Claude Shannon als den wichtigsten Einflussfaktor ihrer Arbeit.

Lenstras " Universal Security " veranschaulicht die Energiemenge, die benötigt wird, um das symmetrische Kryptosystem mit verschiedenen Schlüssellängen zu "brechen". Es stellte sich heraus, dass das Brechen eines 228 Bit langen, elliptischen Kurvenschlüssels dieselbe Energiemenge erfordert, die zum Kochen des gesamten Wassers auf der Erde erforderlich ist. Sie gilt jedoch nur unter Berücksichtigung bekannter Algorithmen und Hardware, da streng genommen niemand weiß, ob es wesentlich effizientere Algorithmen oder Hardware gibt. Der 228-Bit-EC-Schlüssel ist vergleichbar mit dem 2380-Bit-langen RSA-Schlüssel, dazu später mehr. Obwohl bei dieser Schätzung sowohl RSA- als auch EC-Schlüssel in einem asymmetrischen Verschlüsselungsschema verwendet werden, entsprechen solche Schlüssellängen in gewisser Weise einem symmetrischen 128-Bit-Verschlüsselungsschlüssel.

Es ist leicht vorstellbar, dass etwas „Schwer zu berechnendes“ viel Energie und / oder Zeit für die Berechnung benötigt. Wir neigen dazu zu denken, dass Computer "alles berechnen" können, aber es stellt sich heraus, dass es nicht wahr ist. Erstens gibt es unbestreitbare Beispiele wie das Halteproblem, obwohl wir auf dem Gebiet der Kryptographie diese Falle umgehen können. Zweitens kann die Zeit, die für die Ausführung eines bestimmten Algorithmus benötigt wird, beliebig hoch sein. Das nutzen wir in der Kryptographie. Ein Problem wird als „einfach“ zu berechnen angesehen, wenn die für die Ausführung des jeweiligen Algorithmus erforderliche Zeit wie bei einem Polynom von der Eingangsgröße (in Bits gemessen) abhängt:$$ $ inline $ T (n) = O (n ^ k) $ inline $ für eine positive Konstante$$ $ inline $ k $ inline $ . Im Bereich der rechnergestützten Komplexitätstheorie bilden solche Probleme die P-Komplexitätsklasse .

Die P-Komplexitätsklasse ist fast zentral, da sie das Problem darstellt, für das ein deterministischer polynomieller Zeitalgorithmus existiert. Eine andere Komplexitätsklasse ist der NP (die Probleme, die „schwer“ zu berechnen sind), der eine Reihe von Entscheidungsproblemen darstellt, dh Probleme, die eine Antwort mit „Ja“ oder „Nein“ erfordern und deren Beweis in Polynomzeit überprüfbar ist. Sehen Sie hier das Wort „Beweis“? Hier gelangen wir zu den Falltürfunktionen, die zur NP-Komplexitätsklasse gehören.


Credits: xkcd

Einwegfunktionen; Trapdoor-Funktionen

Per Definition ist eine Einwegfunktion eine Funktion, die bei jeder Eingabe einfach zu berechnen ist, die sich jedoch nur schwer umkehren lässt, dh die ursprüngliche Eingabe nur bei gegebener Ausgabe berechnet. "Einfach" und "Schwer" beziehen sich auf die obigen Definitionen der Komplexitätstheorie. Interessanterweise ist die Existenz von Einwegfunktionen nicht (mathematisch) bewiesen, da ihre Existenz beweisen würde, dass die P- und NP-Komplexitätsklassen nicht gleich sind, während entweder P gleich NP ist oder nicht, heutzutage ein offenes Problem ist. Denken Sie also daran, dass jede moderne Kryptographie auf unbewiesenen Hypothesen beruht.

In ihrer Originalarbeit stellen Diffie und Hellman nun eine weitere Generation der Einwegfunktionen vor, die sie als "Falltürfunktionen" bezeichnen. Wie unterscheiden sie sich?
Wie sie in ihrem Leitartikel erklären:

In einem Kryptosystem mit öffentlichem Schlüssel werden die Verschlüsselung und Entschlüsselung durch getrennte Schlüssel E und D geregelt, so dass die Berechnung von D aus E rechnerisch nicht durchführbar ist (z. B. erforderlich)$$ $ inline $ 10 ^ {100} $ inline $ Anweisungen). Der Verschlüsselungsschlüssel E kann [in einem Verzeichnis] ​​ohne Beeinträchtigung des Entschlüsselungsschlüssels D offenbart werden. Dies ermöglicht jedem Benutzer des Systems, eine Nachricht an einen anderen Benutzer zu senden, der derart verschlüsselt ist, dass nur der beabsichtigte Empfänger sie entschlüsseln kann. .. Das Problem der Authentifizierung ist möglicherweise ein noch größeres Hindernis für die universelle Einführung der Telekommunikation für Geschäftstransaktionen als das Problem der Schlüsselverteilung ... [es] ... ist der Kern eines jeden Systems, das Verträge und Abrechnungen umfasst.

Üblicherweise werden die Kryptographiezeichen „Alice“ und „Bob“ (für eine sichere Kommunikation) häufig verwendet, um das Konzept des öffentlichen Schlüssels zu erläutern. Alice und Bob sind sich über große ganze Zahlen einig$$ $ inline $ n $ inline $ und$$ $ inline $ g $ inline $ mit$$ $ inline $ 1 <g <n $ inline $ . Die Auswahl wirkt sich auf die Sicherheit des Systems aus. „Der Modul$$ $ inline $ n $ inline $ sollte eine Primzahl sein; was noch wichtiger ist$$ $ inline $ (n-1) / 2 $ inline $ sollte auch eine Primzahl sein <...> und$$ $ inline $ g $ inline $ sollte eine primitive Wurzel Modulo sein$$ $ inline $ n $ inline $ <...> [und]$$ $ inline $ n $ inline $ sollte <...> mindestens 512 Bit lang sein. ” Das Diffie - Hellman - Protokoll kann in 5 Schritten in elementarer Form angegeben werden.

1. Alice wählt$$ $ inline $ x $ inline $ (eine große zufällige ganze Zahl) und berechnet$$ $ inline $ X = g ^ x \ bmod n $ inline $
2. Bob wählt$$ $ inline $ y $ inline $ (eine große zufällige ganze Zahl) und berechnet$$ $ inline $ Y = g ^ y \ bmod n $ inline $
3. Alice schickt$$ $ inline $ X $ inline $ zu Bob, während Bob sendet$$ $ inline $ Y $ inline $ zu Alice (sie behalten$$ $ inline $ x $ inline $ und$$ $ inline $ y $ inline $ Geheimnis voneinander)
4. Alice rechnet$$ $ inline $ k = Y ^ x \ bmod n $ inline $
5. Bob rechnet$$ $ inline $ k '= X ^ y \ bmod n $ inline $

Infolgedessen haben Alice und Bob den gleichen Wert$$ $ inline $ k = k '$ inline $ das dient als gemeinsames Geheimnis.

Die Trapdoor-Funktion ist eine Einwegfunktion, die es ermöglicht, ihre Umkehrung zu finden, wenn eine spezielle Information namens "Trapdoor" vorhanden ist. Klingt einfach, obwohl es ziemlich schwierig ist, solche Funktionen zu finden - die erste realisierbare Methode bestand in der Implementierung eines asymmetrischen Verschlüsselungsalgorithmus für die Kryptografie mit öffentlichem Schlüssel, der RSA genannt wurde und nach seinen Entwicklern Ron Rivest, Adi Shamir und Leonard Adleman benannt wurde.

RSA

In RSA beruht die Härte der Invertierung der Funktion auf der Tatsache, dass das Factoring (Finden von Primmultiplikatoren einer Zahl) viel mehr Zeit benötigt als das Multiplizieren, oder sollten wir hier sagen, dass es keine polynomielle Zeitmethode zum Factoring großer Ganzzahlen auf einem klassischen Computer gibt Es wurde jedoch nicht nachgewiesen, dass keines existiert.

In RSA gibt es wie in jedem anderen Verschlüsselungssystem mit öffentlichem Schlüssel zwei Schlüssel: öffentlich und privat. RSA verwendet die Eingangsnachricht (dargestellt als Bitfolge) und wendet eine mathematische Operation (Exponentiation modulo a big integer) auf sie an, um ein Ergebnis zu erhalten, das nicht vom Zufall zu unterscheiden ist. Die Entschlüsselung verwendet dieses Ergebnis und wendet einen ähnlichen Vorgang an, um die ursprüngliche Nachricht wiederherzustellen. Bei der asymmetrischen Kryptographie erfolgt die Verschlüsselung mit dem öffentlichen Schlüssel und die Entschlüsselung mit dem privaten.

Wie? Weil die Operanden zu einer endlichen zyklischen Gruppe gehören (eine Menge von Ganzzahlen mit Multiplikation in modularer Arithmetik). Computer können mit willkürlich großen Zahlen nicht gut umgehen, aber zum Glück besteht unsere zyklische Gruppe von Ganzzahlen darin, eine Operation mit der Bezeichnung "Umlauf" auszuführen - eine Zahl, die größer als das zulässige Maximum ist, wird auf eine Zahl in dem gültigen Bereich umlaufen, den wir betreiben . Dies ermöglicht es uns, mit Schlüsseln zu arbeiten, die nicht länger als sind. In der Kryptographie mit elliptischen Kurven werden auch zyklische (multiplikative) Gruppen verwendet, die jedoch etwas anders aufgebaut sind, wie wir später sehen werden.

Grundsätzlich nimmt RSA zwei große Primzahlen und multipliziert sie, um den sogenannten Modul zu erhalten. Alle anderen zu behandelnden Zahlen liegen zwischen Null und dem Modul. Der Modul soll Teil des öffentlichen Schlüssels sein, und seine Bitlänge bestimmt die Schlüssellänge. Der zweite Teil des öffentlichen Schlüssels ist eine Zahl zwischen Null und dem Euler-Totienten (moderne RSA-Implementierung verwendet den Carmichael-Totienten anstelle von Euler) des Moduls mit einigen zusätzlichen Einschränkungen. Schließlich soll der private Schlüssel durch Lösen einer modularen Gleichung berechnet werden. Um eine Zahl zu verschlüsseln, erhöhen wir sie einfach auf die Potenz, die dem öffentlichen Schlüssel entspricht, und um eine Zahl zu entschlüsseln, erhöhen wir sie auf die Potenz, die dem privaten Schlüssel entspricht. Aufgrund der Zyklizität der Gruppe erhalten wir die ursprüngliche Nummer zurück.

Heutzutage gibt es zwei signifikante Probleme mit der RSA, eines ist eine Konsequenz des anderen. Wenn die Länge eines Schlüssels (d. H. Die Anzahl seiner Bits) zunimmt, nimmt der Komplexitätsfaktor nicht so schnell zu, wie man es erwarten könnte. Das liegt daran, dass es einen subexponentiellen (aber immer noch superpolynomiellen ) Faktorisierungsalgorithmus gibt . Um eine angemessene Sicherheitsstufe beizubehalten, muss die Länge des RSA-Schlüssels etwas schneller als die Länge des ECC-Schlüssels wachsen. Aus diesem Grund sind die meisten heute verbreiteten RSA-Schlüssel entweder 2048 oder 3072 Bit lang.

Etwas später werden wir in Zahlen sehen, wie sich die Länge des Schlüssels auf die Gesamteffizienz des Kryptosystems auswirkt, indem wir das mit der Berechtigung Let's Encrypt signierte RSA- und ECDSA-Zertifikat vergleichen.

( E lliptic C urve) Digitaler S ignature A- Algorithmus

Die Suche nach einer besseren Falltürfunktion führte die Kryptografen schließlich zu einem sich Mitte der 80er Jahre aktiv entwickelnden Zweig der Mathematik, der elliptischen Kurven gewidmet war.

Es wäre die ultimative Aufgabe, die Kryptographie mit elliptischen Kurven in einem Artikel zu beschreiben, also werden wir es nicht tun. Schauen wir uns stattdessen eine Trapdoor-Funktion mit elliptischen Kurven an, die auf dem Problem des diskreten Logarithmus basiert.

Es gibt viele Grundlagen und tiefere Einführungen in die Kryptographie mit elliptischen Kurven, und wir würden Andrea Corbellinis „ECC: eine sanfte Einführung“ besonders empfehlen, wenn Sie sich für Mathematik interessieren.

Was uns interessiert, sind eher "einfache" Parameter.

Die elliptische Kurve wird durch eine Gleichung wie folgt definiert:$$ $ inline $ y ^ 2 = x ^ 3 + ax + b $ inline $
Eine solche Kurve wird benötigt, um eine zyklische Untergruppe über einem endlichen Feld aufzubauen. Daher werden folgende Parameter verwendet:

• Die Blütezeit$$ $ inline $ p $ inline $ das gibt die Größe des endlichen Feldes an;
• Die Koeffizienten$$ $ inline $ a $ inline $ und$$ $ inline $ b $ inline $ der elliptischen Kurvengleichung;
• Der Ausgangspunkt$$ $ inline $ g $ inline $ das erzeugt die erwähnte Untergruppe;
• Die Bestellung$$ $ inline $ n $ inline $ der Untergruppe;
• Der Cofaktor$$ $ inline $ h $ inline $ der Untergruppe.

Zusammenfassend ist der Domänenparameter für unsere Algorithmen das Sextuplett$$ $ inline $ (p, a, b, g, n, h) $ inline $ .
Solche elliptischen Kurven wirken über das endliche Feld$$ $ inline $ \ mathbb {F} _p $ inline $ wo$$ $ inline $ p $ inline $ ist eine ziemlich große Primzahl. Wir haben also eine Reihe von Ganzzahlen modulo$$ $ inline $ p $ inline $ , wobei Operationen wie Addition, Subtraktion, Multiplikation, additive Inverse, multiplikative Inverse möglich sind. Addition und Multiplikation funktionieren ähnlich wie die modulare oder sogenannte "Clock" -Arithmetik, die wir in den RSA "Wrap Around" gesehen haben.
Da die Kurve bei jedem Punkt symmetrisch zur x-Achse ist$$ $ inline $ P $ inline $ können wir nehmen$$ $ inline $ −P $ inline $ der Punkt gegenüber sein. Wir nehmen$$ $ inline $ −O $ inline $ gerecht zu sein$$ $ inline $ O $ inline $ .
Die Addition für Kurvenpunkte wird auf eine Weise definiert, die bestimmten Punkten entspricht$$ $ inline $ P $ inline $ und$$ $ inline $ Q $ inline $ können wir eine Linie zeichnen, die beide Punkte schneidet und eine Kurve in einem dritten Punkt schneidet$$ $ inline $ R $ inline $ so das$$ $ inline $ P + Q = -R $ inline $ und$$ $ inline $ P + Q + R = 0 $ inline $ .

Werfen wir einen Blick auf die Erklärung von Marc Hughes :

Oben ist eine Linie mit konstanter Steigung dargestellt, die sich entlang der Oberfläche des Torus erstreckt. Diese Linie verläuft durch zwei zufällig ausgewählte ganzzahlige Punkte auf der Kurve.



Um zwei Punkte zum Diagramm hinzuzufügen, zeichnen Sie eine Linie vom ersten ausgewählten Punkt$$ $ inline $ P $ inline $ zum zweiten ausgewählten Punkt$$ $ inline $ Q $ inline $ , und verlängern Sie die Linie, bis sie einen anderen Punkt im Diagramm schneidet$$ $ inline $ -R $ inline $ bei Bedarf über die Grundstücksgrenzen hinweg erweitern.

Wenn Sie einen ganzzahligen Punkt abfangen, spiegeln Sie den Punkt vertikal in der Mitte des Diagramms (eine orange gepunktete Linie), um den neuen Punkt zu finden$$ $ inline $ R $ inline $ in der Grafik. Deshalb$$ $ inline $ P + Q = R $ inline $ .

Die Multiplikation mit einem Skalar ist jetzt trivial:$$ $ inline $ n \ cdot P = P + P + P + \ dots + P $ inline $ (hier sind$$ $ inline $ n $ inline $ summands).

Die Falltürfunktion liegt hier im Problem des diskreten Logarithmus (für elliptische Kurven), nicht in der Faktorisierung, die wir im Abschnitt RSA untersucht haben. Das Problem ist: Wenn wir es wissen$$ $ inline $ P $ inline $ und$$ $ inline $ Q $ inline $ , was ist so$$ $ inline $ k $ inline $ , das$$ $ inline $ Q = k \ cdot P $ inline $ ?

Sowohl das Faktorisierungsproblem (das dem RSA zugrunde liegt) als auch der diskrete Logarithmus für elliptische Kurven (der die Basis für ECDSA und ECDH ist) sollen schwierig sein, d. H. Es sind keine Algorithmen bekannt, um dieses Problem in der Polynomzeit für einen gegebenen Schlüssel zu lösen Länge.

Während normalerweise jeder beschämt ist, den Schlüsselaustausch (ECDH) mit dem Signaturalgorithmus (ECDSA) zu mischen, müssen wir erklären, wie sie zusammenarbeiten. Ein modernes TLS-Zertifikat enthält in unserem Fall einen öffentlichen Schlüssel für das vom Ellipsenkurvenalgorithmus generierte Schlüsselpaar, das normalerweise von einer übergeordneten Behörde signiert wird. Der Client überprüft die Signatur des Servers und erhält das gemeinsame Geheimnis. Das gemeinsame Geheimnis wird in einem symmetrischen Verschlüsselungsalgorithmus wie AES oder ChaCha20 verwendet. Das Prinzip bleibt jedoch dasselbe: Vereinbaren Sie Domänenparameter (das Sextuplet), und erhalten Sie das Schlüsselpaar, wobei der private Schlüssel eine zufällig ausgewählte Ganzzahl ist (der Multiplikand von$$ $ inline $ Q = k \ cdot P $ inline $ ) und der öffentliche Schlüssel ist ein Punkt auf der Kurve. Signaturalgorithmen verwenden den Basispunkt$$ $ inline $ g $ inline $ Dies ist ein Generator für eine Untergruppe großer Primzahlen$$ $ inline $ n $ inline $ , so dass$$ $ inline $ n \ cdot G = 0 $ inline $ , wobei 0 das Identitätselement ist. Die Signatur belegt, dass die sichere Verbindung mit der authentischen Partei hergestellt wird - einem Server, auf dem das TLS-Zertifikat (öffentlicher Schlüssel) von einer Zertifizierungsstelle für den angegebenen Servernamen signiert ist.

(EC) DH (E) + ECDSA = Aktuelle Handshake-Form

In modernen TLS (1.3) generieren der Client und der Server ihr öffentlich-privates Schlüsselpaar im laufenden Betrieb, während die Verbindung hergestellt wird. Dies wird als kurzlebige Version des Schlüsselaustauschs bezeichnet. Die beliebtesten Browser-TLS-Bibliotheken unterstützen dies. Meistens verwenden sie die von Daniel J. Bernstein (djb) eingeführte elliptische Kurve Edwards 25519 , die 128-Bit-Sicherheit bietet. Seit 2014 verwendet openssh diese Kurve für die Schlüsselpaarerstellung. Im Jahr 2019 unterstützen Browser jedoch keine TLS-Sitzungen mit Servern, die ein Zertifikat mit einem öffentlichen EdDSA-Schlüssel haben.

Kommen wir jedoch zum Ende des Jahres 2019 mit TLS 1.3 zurück.

Die Schlüsselaustauschmechanismen in TLS 1.3 sind auf (EC) DH (E) -basiert beschränkt (mit x25519 wird dies in clientseitigen TLS-Bibliotheken der meisten gängigen Browser sowie in serverseitigen TLS-Bibliotheken wie OpenSSL unterstützt). Die Liste der Chiffresuiten enthält nur drei Einträge: TLS_AES_128_GCM_SHA256, TLS_AES_256_GCM_SHA384 und TLS_CHACHA20_POLY1305_SHA256. Für diejenigen unter Ihnen, die wissen, wie die Chiffresuiten in der TLS 1.2-Version benannt wurden, ist es sofort ersichtlich, dass der Schlüsselaustauschmechanismus jetzt vom Namen der Chiffresuite „getrennt“ ist und auch die statischen Austauschmodi RSA und Diffie-Hellman entfernt wurden von der Spezifikation ganz. Sogar die auf PSK basierende Sitzungswiederaufnahme erfolgt über ECDHE in TLS 1.3. Dies gilt auch für benutzerdefinierte DH-Parameter, die derzeit nicht zulässig sind, sodass nur die in der endgültigen Protokollspezifikation als sicher vereinbarten Parameter übrig bleiben.

Es ist interessant, dass es heutzutage einen erheblichen Unterschied in der Funktionsweise asymmetrischer Verschlüsselungsalgorithmen gibt. Bei ECC (und insbesondere ECDSA-Zertifikaten) verwenden wir kleinere Schlüssel, um im Vergleich zu RSA ein „komfortables“ Sicherheitsniveau zu erreichen. Dies ermöglicht die Verwendung eines stärkeren asymmetrischen Verschlüsselungsalgorithmus und von Schlüsselaustauschmechanismen auf kleineren Geräten und manchmal sogar in Dingen, die im Allgemeinen nicht als Gerät (Smartcard) betrachtet werden.

Zunächst muss erwähnt werden, was „hybrides Kryptosystem“ im Sinne von TLS 1.3 bedeutet.
Ein hybrides Kryptosystem ist dasjenige, das eine asymmetrische Verschlüsselung (öffentlicher Schlüssel) verwendet, um ein gemeinsames Geheimnis herzustellen, das ferner als Schlüssel in einem symmetrischen Strom oder einer Blockverschlüsselung verwendet wird.

Zweitens Public-Key-Infrastruktur und Zertifikate. Interessanterweise erwähnte Martin Hellman in seinem Interview von 2004 einen „nicht gesungenen Helden“, Loren Kohnfelder, dessen MIT-Bachelorarbeit eine Baumstruktur der heute als Public-Key-Infrastruktur bekannten Infrastruktur vorstellte. Kehren wir dennoch zu Zertifikaten zurück.

Die Tatsache, dass der Server wirklich über den privaten Schlüssel verfügt, wird durch seine Signatur sichergestellt, die mit dem öffentlichen Schlüssel des Servers überprüft werden kann. Das Zertifikat stellt sicher, dass ein öffentlicher Schlüssel zu einem bestimmten Server gehört. Dies bedeutet, dass Sie eine sichere Kommunikation mit der bestimmten Partei und nicht mit einem Betrüger herstellen. Ihre Bank, kein Cyberkrimineller. In TLS 1.3 gibt es eine erhebliche Verbesserung gegenüber dem vorherigen Verhandlungsformat: Der Server signiert alle Informationen, die er bis zu diesem Zeitpunkt hat: die Begrüßung des Clients und des Servers, einschließlich der ausgehandelten Verschlüsselung. Werfen wir einen Blick auf den entsprechenden Abschnitt des RFC 8446 :

Client Server Key ^ ClientHello Exch | + key_share* | + signature_algorithms* | + psk_key_exchange_modes* v + pre_shared_key* --------> ServerHello ^ Key + key_share* | Exch + pre_shared_key* v {EncryptedExtensions} ^ Server {CertificateRequest*} v Params {Certificate*} ^ {CertificateVerify*} | Auth {Finished} v <-------- [Application Data*] ^ {Certificate*} Auth | {CertificateVerify*} v {Finished} --------> [Application Data] <-------> [Application Data] 

In TLS 1.3 sendet der Client die Schlüsselfreigabe (zusammen mit den erforderlichen Parametern) und die Signaturalgorithmen sofort in der ersten Nachricht (Client Hello). Die zum Austausch mit dem Server erforderlichen Schlüssel werden im Hintergrund erstellt, ohne dass der Benutzer dies bemerkt. Sie werden weiter mit dem Server ausgetauscht, um ein gemeinsames Geheimnis aus geheimen Pre-Master-Schlüsseln zu erstellen, die eingerichtet wurden, als der Server seine Nachricht (Server Hello) an den Client antwortete.
Auf der Seite „Server Hello“ sehen Sie das Zertifikat *, das an den Client übertragen wird, sowie den Teil Certificate Verify *, der überprüft, ob der Teilnehmer den privaten Schlüssel für den entsprechenden öffentlichen Schlüsseleintrag besitzt, und erstellt den Sitzungsschlüssel (symmetrisch) if Alles läuft wie geplant - was bedeutet, dass die Seite, die die Daten anfordert (Client), die antwortende Seite (Server) erfolgreich verifiziert hat, wodurch ein gemeinsames Geheimnis entsteht.

In dieser Übertragung sind zwei wesentliche Vorgänge verborgen - das Erstellen einer Signatur und das Überprüfen der Signatur. Diese werden auf beiden Seiten der Kommunikation vorgenommen, da „Signatur“ im Wesentlichen ein Beweis dafür ist, dass die Partei tatsächlich über den privaten Schlüssel verfügt, der dem öffentlichen Schlüssel entspricht, dass die Daten vom Unterzeichner stammen und die Nachricht während der Übertragung nicht geändert wurde.

Wie wir weiter sehen werden, ist der Signiervorgang bei RSA am teuersten. Da wir mit einem 2048 oder 3072 Bit langen Schlüssel signieren, wird durch diesen Vorgang der Server erheblich stärker belastet als der Client, der eine solche Signatur überprüft.

Mit ECDSA haben wir kleinere Schlüssel (wir werden uns das ECDSA mit NIST P-256 (oder dem secp256v1) ansehen), aber komplexere Operationen. Infolgedessen kann es als "verkehrter" RSA angesehen werden - der Client wird durch die Signaturüberprüfungsberechnung am meisten geladen, während der Server die Signaturerstellung problemlos abwickelt. Die Messungen bestätigen dies, siehe Abschnitt „Ein bisschen Benchmark“.

Dieser Effekt skaliert das heutige Internet auf einfache Weise - da moderne Clients fast genauso leistungsfähig sind wie die Server (unter Berücksichtigung der CPU-Kernfrequenz), können sie den teuren Vorgang effektiv in Kauf nehmen. Der Server kann seinerseits die freigegebenen Funktionen verwenden, um mehr Signaturen zu erstellen und mehr Sitzungen einzurichten.

Lassen Sie uns die Zertifikatsignatur verschlüsseln

Um dem Leser einige praktische und praktische Anweisungen zum Erstellen eines TLS-fähigen Servers mit dem von der Let's Encrypt-Autorität signierten ECDSA-Schlüsselpaar zu geben, haben wir uns entschlossen, einen vollständigen Prozess zum Erstellen eines erforderlichen Schlüsselpaars zu veranschaulichen um eine CSR (Certificate Signing Request) für Let's Encrypt zu erstellen und als Ergebnis das erforderliche ECDSA-Zertifikat für unseren Server zu erhalten.

Wir müssen einen privaten Schlüssel generieren, um fortzufahren. Wir werden die OpenSSL-Bibliothek verwenden.
Das OpenSSL-Handbuch beschreibt die Generierung von EC-Schlüsseln durch einen speziellen Befehl, der speziell für den elliptischen Kurvenast des Generierungsalgorithmus bestimmt ist.

 openssl ecparam -genkey -name -secp256v1 -out privatekey.pem 

Um zu überprüfen, ob die OpenSSL-Bibliothek alles richtig gemacht hat, können wir den Befehl ec ausführen.

 openssl ec -in privatekey.pem -noout -text 

Die Ausgabe zeigt uns die angegebene Kurve, mit der der Schlüssel erstellt wurde.

Der nächste Schritt ist für die Erstellung des CSR sehr wichtig. Damit Sie nicht alle Informationen eingeben müssen, um das Zertifikat zu erhalten, benötigen Sie die Konfigurationsdatei. Glücklicherweise hat Mozilla die gesamte Arbeit für uns erledigt und den „ SSL Configuration Generator “ eingeführt. Dort können Sie aus beliebigen verfügbaren Serveroptionen auswählen. Die reine OpenSSL-Konfiguration, die auf der Seite des Generators nicht vorhanden ist, würde ungefähr so ​​aussehen:

 [ req ] prompt = no encrypt_key = no default_md = sha256 distinguished_name = dname req_extensions = reqext [ dname ] CN = example.com emailAddress = admin@example.com [ reqext ] subjectAltName = DNS:example.com, DNS:*.example.com 

Hinweis: Es ist nicht erforderlich, über CNF zu verfügen. Andernfalls werden Sie aufgefordert, diese Details in die Befehlszeile einzugeben.

Folgen Sie nun der Erstellung eines CSR. Hier haben wir einen praktischen OpenSSL-Befehl.

 openssl req -new -config -pathtoconfigfile.cnf -key privatekey.pem -out csr.pem 

Wir können auch die Richtigkeit einer neu erstellten CSR überprüfen.

 openssl req -in csr.pem -noout -text -verify 

Hier sind wir zu einer letzten Phase gekommen - mit einem ACME-Client, certbot, um unsere Zertifikatsignierungsanforderung an Let's Encrypt weiterzuleiten.

Certbot hilft Ihnen, das erforderliche Zertifikat zu erhalten, und bietet eine Vielzahl von Optionen. Wenn Sie mit der Verschlüsselung mit öffentlichen Schlüsseln und der PKI-Infrastruktur von 2019 noch nicht --dry-run sind, sollten Sie --dry-run bevor Sie versuchen, das Zertifikat für eine Domain Ihrer --dry-run zu erhalten.

 certbot certonly --dry-run --dns-somednsprovider --domain “example.com” --domain “*.example.com” --csr csr.pem 

In diesem Fall überprüft der Certbot-Client, ob die Liste der angeforderten Domänen (in der Befehlszeile) mit den in der Zertifikatsignierungsanforderung aufgeführten Domänen übereinstimmt. --dns-somednsprovider Befehl --dns-somednsprovider eine --dns-somednsprovider Lüge, da Sie auf vielfältige Weise nachweisen können, dass Let's Encrypt Sie im Besitz eines bestimmten Teils des Internetverkehrs sind. Wenn Sie jedoch einen öffentlichen Cloud-Hosting-Anbieter verwenden, z. B. DigitalOcean, Hetzner, Amazon, Azure, usw., gibt es wahrscheinlich eine natürlichere Möglichkeit, die erforderlichen Informationen bereitzustellen, da Ihr Anbieter bereits ein Integrationstool erstellt hat.

Wenn Sie sich nachher sicher sind, ob die Parameter, mit denen Sie Ihre CSR über einen Certbot-Client an Let's Encrypt übergeben, korrekt sind, schließen Sie den Parameter --dry-run aus Ihrem Befehl aus und fahren Sie fort.

Bei Erfolg würde der Client mehrere Zertifikate als Ausgabe erzeugen: das signierte Zertifikat selbst, die Stamm- und Zwischenzertifikate und die Kombination dieser Zertifikate als letztgenannte Zertifikatskette im PEM-Dateiformat.

OpenSSL verfügt über einen Befehl, mit dem wir die Zertifikate überprüfen können:

 openssl x509 -in chainfilepath.pem -noout -text 

An diesem Punkt wird deutlich, dass Let's Encrypt das Zertifikat mit SHA256 Digest signiert hat. Darüber hinaus fallen die Signaturen für ECDSA-Stamm- und Zwischenprodukte unter den Abschnitt „Bevorstehende Funktionen“. Dies bedeutet effektiv, dass Sie derzeit nur RSA-Zwischenprodukte erhalten. Aber das ist in Ordnung, da Sie immer noch den öffentlichen ECDSA-Schlüssel verwenden.

Am Ende dieses Abschnitts möchten wir etwas zur Länge der Tasten sagen. In der Informationssicherheit wird häufig die Sicherheitsstufe 2 ^ x angegeben, wobei x die Bitlänge ist (RSA ist hier eine Ausnahme, da es etwas langsamer als exponentiell wächst). Um zu schätzen, wie die für verschiedene Algorithmen verwendeten Schlüssel einander entsprechen, verweisen wir auf die OpenSSL- Wiki-Seite .
Wie Sie sehen, sind die Unterschiede ziemlich ausgeprägt. Obwohl mit Let's Encrypt keine Zertifikate außerhalb der elliptischen Kurvenschlüssel 256 (secp256v1) und 384 (secp384r1) signiert werden konnten.

Bekannte Probleme und Ausnahmen sowie die NSA

Credits: xkcd

Wahrscheinlich war das zentrale Problem bei der Verwendung der Kryptographie mit elliptischen Kurven im Laufe der Jahre die Notwendigkeit eines sehr sorgfältig ausgearbeiteten Zufallszahlengenerators, um Schlüssel mit der erforderlichen Sicherheitsstufe zu erstellen.

Es gab einen massiven Skandal um den Dual_EC_DRBG- Algorithmus (Dual Elliptic Curve Deterministic Random Bit Generator), dessen Auflösung viele Jahre in Anspruch nahm. Es besteht auch Unsicherheit in Bezug auf ECC-Patente, da bekannt ist, dass viele von ihnen der Certicom-Firma gehörten, die von Blackberry erworben wurde. Es gibt auch Unternehmen, von denen bekannt ist, dass sie die Verwendung von ECC von Blackberry zertifizieren. Natürlich gibt es in einigen NIST-Standards ein einfaches Misstrauen, das von der NSA oder einer anderen US-amerikanischen Durchsetzungs- und Überwachungsbehörde beeinträchtigt werden könnte oder nicht.

Die Implementierungsseite eines Problems ist eine ganz andere Frage. Im Jahr 2010 wurde auf der PlayStation 3-Konsole ein privater Schlüssel von Sony wiederhergestellt, da der ECDSA-Algorithmus nicht ordnungsgemäß implementiert wurde. Die statische Zufallszahl machte die Trapdoor-Funktion lösbar. OpenSSL litt auch im folgenden Jahr darunter, dass die Sicherheitsanfälligkeit, die das Abrufen eines privaten Schlüssels mithilfe eines Timing-Angriffs ermöglichte, schnell behoben wurde. Weitere Informationen finden Sie im Originaldokument .

2013 präsentierte eine Gruppe von Forschern auf der RSA-Konferenz ihre „ Randomly Failed! Artikel über Sicherheitslücken in der SecureRandom-Java-Klasse. Ein halbes Jahr später ging es um Android Bitcoin- Geldbörsen, die mit nicht genügend kryptografisch sicherem PRNG erstellt wurden.

Aufgrund schwerwiegender serieller Sicherheitslücken veröffentlichte die IETF im August 2013 einen RFC 6979 , der eine deterministische Generation von k beschreibt, die bei der Schlüsselerstellung verwendet wurde. Wir könnten sagen, dass eine solche Maßnahme das Problem behoben hat, aber wir werden es nicht tun - Forscher könnten aufgrund unnötiger Abweichungen von den Protokollspezifikationen jederzeit Probleme in zahlreichen Implementierungen finden.

Über die NSA. Wenn Sie noch nichts über die Geschichte von Dual_EC_DRBG gehört haben - nehmen Sie sich etwas Zeit und lesen Sie die entsprechenden Artikel. Sie werden es nicht bereuen, auf Einzelheiten eingegangen zu sein. Edward Snowden ist ein Teil dieser Geschichte, weil die Enthüllungen von 2013 den früheren Verdacht bewiesen haben. Dies führte dazu, dass viele prominente Kryptografen das Vertrauen in NIST verloren, da diese Organisation viele der Kurven und weiteren Algorithmen entwarf und beschrieb, die ECDSA zugrunde lagen.

Daniel Bernsteins 25519-Kurve und DH-Funktion sind die Antwort auf beide Probleme. Wie wir bereits beschrieben haben, ist ein Übergang zu EdDSA zwar langsam, aber offensichtlich. Selbst mit den NIST-Kurven wurden noch keine Hinweise auf ihre Verwundbarkeit gefunden, und wie bereits erwähnt, waren zufällige Erfahrungen recht aufschlussreich.

Abschließend möchten wir das Zitat von John von Neumann zitieren: "Wer versucht, Zufallszahlen mit deterministischen Mitteln zu generieren, lebt natürlich in einem Zustand der Sünde."

Ein bisschen Benchmark

Wir haben einen NGINX 1.16.0-Server mit OpenSSL 1.1.1d verwendet, um diese Benchmarks mit verschiedenen Zertifikaten auszuführen. Wie bereits erwähnt, lässt Let's Encrypt derzeit nur die Algorithmen prime256v1 und secp384r1 für Zertifikatsignierungsanforderungen zu und bietet keine Root- und Intermediär-ECDSA-Zertifikate, die wahrscheinlich bei dieser Funktion zum Zeitpunkt des Erstellens dieses Artikels funktionieren.
Wie Sie sehen, beträgt der Gesamtunterschied bei der ECDSA-Leistung eines einzelnen Kerns der Intel® Xeon® Silver 4114-CPU bei 2,20 GHz (Start Q3'17) im Vergleich zum weit verbreiteten RSA 2048 das 3,5-fache.

Schauen wir uns nun die OpenSSL-Geschwindigkeitsergebnisse des gleichen Prozessors mit ECDSA und RSA an.
Hier sehen wir eine Bestätigung für die früher gegebene These der unterschiedlichen Rechenkosten für die Vorzeichen- und Überprüfungsoperationen von ECC und RSA. Infolgedessen bietet die derzeit mit TLS 1.3 ECC ausgestattete Version eine deutliche Leistungssteigerung bei der höheren Bit-Sicherheitsstufe im Vergleich zu RSA. Dies ist der wichtigste Grund, warum wir bei Qrator Labs unsere Kunden dazu ermutigen, ECDSA einzuführen. Mit modernen CPUs erhalten Sie fast den fünffachen Unterschied zugunsten von ECDSA.

Wenn Sie daran interessiert sind, wie Ihre CPU kryptografische Berechnungen durchführt, können Sie einen einfachen Befehl openssl speed ausführen. Mit den Parametern -rsa , -ecdsa und -eddsa Sie Benchmark-Ergebnisse für die entsprechenden Signaturalgorithmen.

(Überlagerte) Zukunft

Credits: djb

Es ist ironisch, dass Google während der Vorbereitung dieses Artikels " Erreichen der Quantenherrschaft " angekündigt hat. Bedeutet dies, dass wir gerade in Gefahr sind und alles, was bis zu diesem Moment entwickelt wurde, keine Geheimhaltung bietet?

Nun, nein.

Wie Bruce Schneier in seinem Aufsatz für IEEE-Sicherheit und Datenschutz " Kryptographie nach den Aliens Lands " schrieb, konnte ein schwerer Schlag mit einem ausreichend leistungsfähigen Quantencomputer gegen die (asymmetrische) Kryptographie mit öffentlichem Schlüssel verübt werden. Symmetrische Kryptographie wäre immer noch stark.

Wir möchten Bruce Schneier mit folgenden Worten zitieren:

Es gibt noch ein weiteres Zukunftsszenario, für das kein Quantencomputer erforderlich ist. Während es mehrere mathematische Theorien gibt, die die Einbahnstraße, die wir in der Kryptographie verwenden, untermauern, ist der Nachweis der Gültigkeit dieser Theorien tatsächlich eines der großen offenen Probleme in der Informatik. So wie es einem intelligenten Kryptografen möglich ist, einen neuen Trick zu finden, der es einfacher macht, einen bestimmten Algorithmus zu brechen, können wir uns Aliens mit einer ausreichenden mathematischen Theorie vorstellen, um alle Verschlüsselungsalgorithmen zu brechen. Für uns ist das heute lächerlich. Die Kryptographie mit öffentlichen Schlüsseln ist eine Zahlentheorie und potenziell anfällig für mathematisch veranlagte Aliens. Symmetrische Kryptographie ist so viel nichtlineares Durcheinander, so einfach komplexer zu machen und so einfach, die Schlüssellänge zu erhöhen, dass diese Zukunft unvorstellbar ist. Betrachten Sie eine AES-Variante mit einer Block- und Schlüsselgröße von 512 Bit und 128 Runden. Wenn sich die Mathematik nicht grundlegend von unserem derzeitigen Verständnis unterscheidet, ist dies sicher, bis Computer aus etwas anderem als Materie bestehen und etwas anderes als Raum einnehmen.

Aber wenn das Unvorstellbare passiert, bleibt uns die Kryptographie, die ausschließlich auf der Informationstheorie basiert: Einmal-Pads und ihre Varianten.

Dies ist der Bereich, in dem, abgesehen von der Suche nach Implementierungsfehlern, die meisten Probleme auftreten können. Wenn es eine Gruppe gut finanzierter Mathematiker, Kryptoanalytiker / Kryptographen und Computeringenieure gibt, die daran arbeiten, einige außergewöhnlich komplexe mathematische Probleme (wie das P? = NP) zu beweisen oder zu widerlegen und bis zu diesem Moment erhebliche Ergebnisse zu erzielen, könnten wir in Schwierigkeiten geraten. Es ist jedoch unwahrscheinlich, dass solche Fortschritte in den Bereichen Informatik, Informations- und Rechenfähigkeitstheorien verborgen bleiben, da diese Tatsache die Namen ihrer Schöpfer auf die Seiten der Geschichte und insbesondere der Geschichte der Internet-Lehrbücher schreibt, was für jeden so unbezahlbar ist . Ein solches Szenario könnte also als nahezu unmöglich angesehen werden.

Es ist nicht klar, ob es in den nächsten 5 Jahren Erfolge mit dem Quanten-Computing geben würde, obwohl es bereits mehrere Kryptographie-Primitive gibt, die als für die Welt nach der Quanten geeignet angesehen werden: Gitter, auf supersingulären elliptischen Kurven basierende Isogenese, Hashes und Codes. Im Moment experimentieren Sicherheitsspezialisten nur mit ihnen. Es besteht jedoch kein Zweifel, dass die Menschheit im Bedarfsfall solche Algorithmen schnell in großem Maßstab einsetzen würde.

Derzeit scheint die Kryptografie mit elliptischen Kurven die perfekte Lösung für das kommende Jahrzehnt zu sein und bietet Sicherheit und Leistung.