🦕 👩🏼‍🎨 🍒 Funktionsweise der Kryptographie mit elliptischen Kurven in TLS 1.3 🤳🏾 🤚🏻 🧐

Ein paar Warnungen an den Leser:

Um den Erklärungsprozess (so weit wie möglich) zu vereinfachen und das Publikationsvolumen zu reduzieren, lohnt es sich, sofort eine Schlüsselreservierung vorzunehmen - alles, was wir über die praktische Seite des Problems schreiben, ist für das TLS-Protokoll Version 1.3 korrekt. Dies bedeutet, dass, obwohl Ihr ECDSA-Zertifikat auf Wunsch mit TLS 1.2 funktioniert, die Beschreibung des Handshake-Prozesses, der Cipher Suites und der Benchmarks auf der neuesten Version des TLS-Protokolls - 1.3 basiert. Wie Sie wissen, gilt dies nicht für die mathematische Beschreibung der Algorithmen, die den Grundlagen moderner kryptografischer Systeme zugrunde liegen.

Dieses Material wurde weder von einem Mathematiker noch von einem Ingenieur geschrieben - obwohl sie dazu beigetragen haben, den Weg durch den mathematischen Dschungel zu ebnen. Vielen Dank an die Mitarbeiter von Qrator Labs.

( E lliptic C urve) D iffie- H ellman ( E phemeral)

Diffie-Hellman-Erbe des 21. Jahrhunderts

Natürlich beginnt dieses Thema nicht mit Whitfield Diffie und nicht mit Martin Hellman. Alan Turing und Claude Shannon leisteten einen großen Beitrag zur Algorithmen- und Informationstheorie sowie zur Kryptoanalyse. Diffie und Hellman wiederum werden von den Autoren der Idee der Kryptographie mit öffentlichen Schlüsseln (auch als asymmetrisch bezeichnet) offiziell anerkannt - obwohl mittlerweile bekannt ist, dass auch in Großbritannien ernsthafte Ergebnisse auf diesem Gebiet erzielt wurden. Sie blieben jedoch lange Zeit geheim - was die beiden im Untertitel genannten Herren zu Pionieren macht.

Was genau

Das mag lustig erscheinen, aber bis zum 6. November 1976 gab es keine verfügbaren Kenntnisse über kryptografische Systeme mit öffentlichem Schlüssel. Whitfield Diffie und Martin Hellman (und tatsächlich Ralph Merkle) - Mathematiker, Computeringenieure und Enthusiasten sowie Kryptologen waren die ersten, die ein geeignetes Konzept vorschlugen.

Während des Zweiten Weltkriegs halfen Kryptographie, Informationen geheim zu halten, und Kryptoanalyse, sie offen zu legen. Die Vereinigten Staaten und das Vereinigte Königreich betrachteten sich als die fortschrittlichsten auf dem Gebiet der Kryptographie. Diese beiden Länder haben kryptografische Algorithmen in die Waffenabteilung aufgenommen und ihr Veto gegen ihre Exporte eingelegt. Gleichzeitig wurde in diesen Ländern die verfügbare und für den kommerziellen oder privaten Gebrauch bestimmte Verschlüsselung gelockert. Aus diesem Grund wurden britische Forscher, die am Government Communications Center (GCHQ) an einem asymmetrischen Schlüsselverteilungsschema arbeiteten und ein ähnliches Konzept entwickelten, erst 1997 von der Community anerkannt, als die bestehenden Beschränkungen für kryptografische Algorithmen und deren Beschreibung im Großen und Ganzen an Bedeutung verloren moralisch veraltet.

Zurück zu unseren Erfindern - was genau haben Diffie und Hellman revolutioniert?

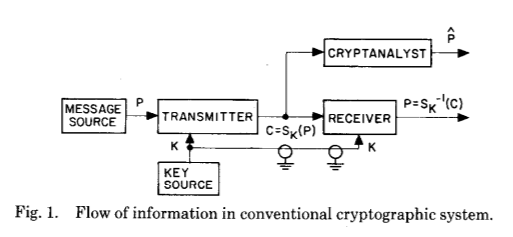
Schauen wir uns zur Erklärung die Abbildung aus der Originalveröffentlichung an, die den enormen Sprung zum Verständnis der Funktionsweise der Kryptographie perfekt widerspiegelt - auch wenn dies zunächst nur theoretisch der Fall ist:
Bild

Und nun zum Folgenden:
Bild

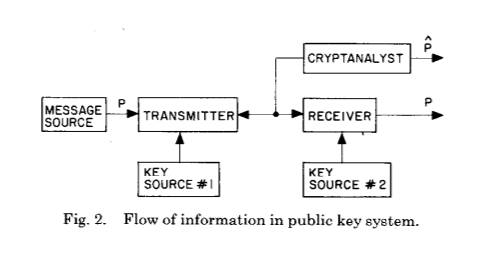
Diese beiden Bilder zeigen die Hauptinnovation von Whitfield Diffie und Martin Hellman nach Jahrhunderten der Entwicklung der Kryptographie und Kryptoanalyse - die Etablierung eines gemeinsamen Geheimnisses als Ergebnis von Berechnungen eines bestimmten Typs.

Schauen wir uns ein weiteres Bild aus Wikipedia an, auf dem verschiedene Farben als Geheimnisse verwendet werden:

Bild

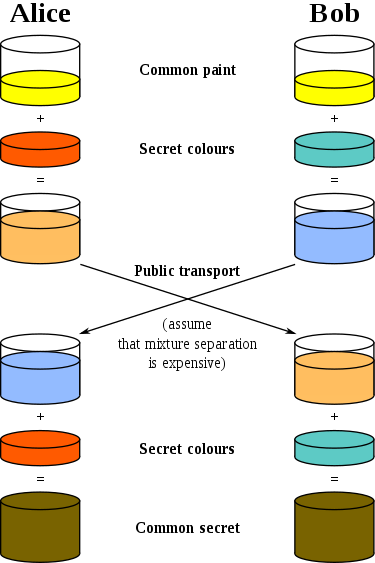
Sie erklärt auch gut, was passiert. Vor der Diffie- und Hellman-Innovation gab es nur einen gemeinsamen Schlüssel in Form eines gemeinsamen Schlüsselerstellungsschemas - er wurde zum Ver- und Entschlüsseln einer Nachricht verwendet. Wenn Sie einen solchen Schlüssel auf die zweite Seite übertragen möchten, muss er über den ursprünglich geschützten Kanal übertragen werden. Alle Einschränkungen eines solchen Schemas werden sofort klar - Sie benötigen einen sicheren (Abhör-) Kommunikationskanal, Sie können denselben Schlüssel nur einmal verwenden , und im Idealfall sollte die Schlüssellänge der Länge der Nachricht entsprechen.

Claude Shannon hat in seiner später freigegebenen Arbeit „Theorie der Kommunikation in geheimen Systemen“ bewiesen, dass alle theoretisch unzerbrechlichen Chiffren die gleichen Eigenschaften haben sollten wie ein einmaliger Chiffrenblock - auch Vernam-Chiffre genannt - mit dem Namen des Erstellers dieses additiven Algorithmus zur Verschlüsselung polyalphabetischer Streams.

Schauen wir uns noch einmal die ursprüngliche wissenschaftliche Veröffentlichung an:
Bild

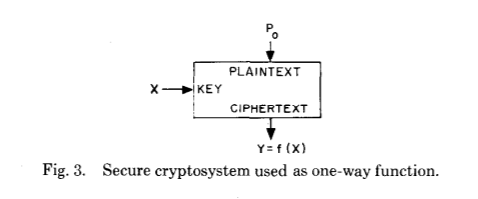
Bevor wir weitermachen, wollen wir uns eine offensichtlich einfache Frage stellen: Wie können zwei, auch sehr intellektuell entwickelte, Menschen einen Durchbruch auf dem Gebiet der Anwendung erzielen, insbesondere angesichts der großen Erfolge der Kriegszeit? Höchstwahrscheinlich aufgrund der Kombination der folgenden Bereiche, die sich damals aktiv entwickelten:

Informationstheorie, formuliert von Claude Shannon;
Algorithmentheorie , die unter anderem von Alonzo Church, John von Neumann und Alan Turing beeinflusst wurde;
Und vor allem die Theorie der Berechenbarkeit , die hauptsächlich auf der Arbeit von Turing basiert.

Wir können sagen, dass sich alle diese Gebiete im gleichen Zeitraum des 20. Jahrhunderts entwickelt und gereift haben. Diffie und Hellman nannten auch Claude Shannon als eine Figur, die ihre Arbeit mehr als andere beeinflusste.

Das Konzept von "Universal Security" von Arjen Lenstra zeigt, wie viel Energie für das "Hacken" eines symmetrischen Kryptosystems mit Schlüsseln unterschiedlicher Länge aufgewendet werden muss. Es stellte sich heraus, dass zum Knacken des 228-Bit-Schlüssels für den Algorithmus, der auf elliptischen Kurven basiert, so viel Energie benötigt wird, wie zum Erhitzen des gesamten Wassers auf der Erde bis zum Siedepunkt ausreicht. Diese Aussage ist jedoch nur dann richtig, wenn wir bekannte Algorithmen berücksichtigen und moderne Geräte verwenden, da streng genommen effizientere Algorithmen oder Geräte möglich sind, deren Existenz jedoch noch nicht bekannt ist. Der 228-Bit-Schlüssel für den EC-Algorithmus zum Hacken von Komplexität ist mit dem 2380-Bit-Schlüssel in RSA vergleichbar, aber dazu später mehr. In diesem Vergleich werden RSA- und EC-Schlüssel in einem asymmetrischen Kryptosystem verwendet. Sie können als äquivalent zu einem 128-Bit-Schlüssel in einem symmetrischen Schema betrachtet werden.

Es ist leicht vorstellbar, dass etwas, das „schwer zu berechnen“ ist, viel Zeit und Energie benötigt, um zu berechnen. Wir neigen dazu zu denken, dass Computer „alles zählen können“, aber es stellt sich heraus, dass dies weit von der Wahrheit entfernt ist.

Erstens gibt es Beispiele für unlösbare Probleme, wie das Stopp-Problem. Auf dem Gebiet der Kryptographie werden solche Aufgaben jedoch nicht verwendet.

Zweitens kann die für einen bestimmten Algorithmus erforderliche Laufzeit beliebig groß sein. Genau das nutzt die Kryptographie. Eine Aufgabe wird rechnerisch als „einfach“ angesehen, wenn die Zeit, die der entsprechende Algorithmus benötigt, um zu funktionieren, von der Größe der Eingabedaten (gemessen in Bits) als Polynom abhängt:

T (n) = O (n^{k})

$T (n) = O (n ^ k)$ für einige positive

k

$k$ . In der Theorie der rechnerischen Komplexität bilden solche Probleme eine Komplexitätsklasse P. Wächst die Laufzeit des Algorithmus beispielsweise exponentiell schneller als ein Polynom, so wird eine solche Aufgabe als rechnerisch "schwierig" angesehen.

Die Komplexitätsklasse P umfasst Aufgaben, für die es einen deterministischen Algorithmus gibt, der in Polynomialzeit arbeitet. Eine andere Komplexitätsklasse ist NP (in der vermutlich „schwierige“ Probleme existieren), ein Lösbarkeitsproblem, dh ein Problem, bei dem die Antwort „Ja“ oder „Nein“ erforderlich ist und dessen Richtigkeit überprüft werden kann, dh der Nachweis der Richtigkeit der Lösung erbracht wird. in der Polynomzeit. Sehen Sie das Wort "Beweis" hier? Dies ist der Ort, an dem wir zu einseitigen Funktionen übergehen, deren Inversionsproblem zur Komplexitätsklasse NP gehört.

Bild

Gepostet von: xkcd

(Einwegfunktionen (mit geheimer Eingabe))

Per Definition ist eine Einwegfunktion eine Funktion, die für jede Eingabe einfach zu berechnen, aber schwierig zu invertieren ist, dh die ursprüngliche Eingabe nur mit dem Ergebnis abzurufen. "Einfach" und "Schwer" beziehen sich auf die oben erwähnte Theorie der rechnerischen Komplexität. Es ist interessant, dass die Existenz von Einwegfunktionen (mathematisch) nicht bewiesen wurde, da ein strenger Beweis ihrer Existenz auch die Ungleichheit der Klassen P und NP beweisen würde, eines der Jahrtausendprobleme und ein dringendes offenes Problem, dessen Lösung einen algorithmischen Durchbruch verspricht. Daher ist zu beachten, dass fast jede moderne Kryptographie auf unbewiesenen Hypothesen basiert.

In ihrer Originalveröffentlichung stellen Diffie und Hellman eine neue Generation von Einwegfunktionen vor, die sie "Einwegfunktionen mit geheimer Eingabe" nennen - in englischer Trapdoor-Funktion. Wie unterscheiden sie sich von Einwegfunktionen?

Schauen wir uns ihre ursprüngliche Erklärung an:

In einem Kryptosystem mit einem öffentlichen Schlüssel werden die Verschlüsselung und Entschlüsselung mit unterschiedlichen Schlüsseln - E bzw. D - durchgeführt, so dass die Berechnung von D aus E praktisch unmöglich ist (z. B. erforderlich ist) $10 ^ {100}$ Anweisungen). Der Verschlüsselungsschlüssel E kann öffentlich bekannt gegeben werden, ohne den Schlüssel D zu gefährden. Dadurch kann jeder Systembenutzer eine Nachricht an einen anderen Benutzer senden, die so verschlüsselt ist, dass nur der erwartete Empfänger sie entschlüsseln kann. <...> Die Authentifizierungsaufgabe ist möglicherweise ein schwerwiegenderes Telekommunikationsproblem für Geschäftstransaktionen im Vergleich zur Verteilung von Schlüsseln, da sie (Authentifizierung) das Herzstück eines jeden Systems darstellt, das mit Verträgen und der Abrechnung von Zahlungen arbeitet.

Normalerweise werden die kryptografischen Zeichen Alice und Bob verwendet, um die Prinzipien des Kryptosystembetriebs zu erläutern (sie streben eine sichere Kommunikation an). Alice und Bob stimmen zu, große Primzahlen zu wählen

n

$n$ und

g

$g$ so dass

1 < g < n

$1 <g <n$ . Diese Auswahl wirkt sich auf die Sicherheit der gesamten Schaltung aus. Nummer

n

$n$ ein Modul genannt sollte einfach sein; außerdem die Nummer

(n - 1) / 2

$(n-1) / 2$ sollte auch einfach sein, aber

g

$g$ muss die primitive Wurzel in der Gruppe der Modulo-Reste sein

n

$n$ ; Außerdem,

n

$n$ sollte groß genug sein - mindestens 512 Bits in binärer Darstellung. Ferner kann das Diffie-Hellman-Protokoll in fünf einfachen Schritten beschrieben werden:

Alice nimmt $x$ (große Primzahl) und berechnet $X = g ^ x \ bmod n$
Bob nimmt $y$ (auch eine große Primzahl) und berechnet $Y = g ^ y \ bmod n$
Alice sendet $X$ Bob, Bob schickt $Y$ Alice ( $x$ und $y$ jeder von ihnen bleibt ein Geheimnis)
Alice rechnet nach $k = Y ^ x \ bmod n$
Bob rechnet $k '= X ^ y \ bmod n$

Infolgedessen erhalten Alice und Bob beim Bau das gleiche Ergebnis.

k = k^{'}

$k = k '$ - ein gemeinsames Geheimnis.

Eine Einwegfunktion mit einer geheimen Eingabe ist also eine solche Einwegfunktion, die umgekehrt werden kann, indem eine spezielle Information, die als "geheime Eingabe" bezeichnet wird, vorliegt. Es hört sich einfach an, aber in der Praxis stellte sich heraus, dass es keine einfache Aufgabe war, eine solche Funktion zu finden - die erste anständige Methode war der Vorläufer einer ganzen Familie von Algorithmen, die auf einem öffentlichen Schlüssel namens RSA basierten.

RSA

In RSA beruht die Komplexität der Invertierung einer Funktion auf der Tatsache, dass die Faktorisierung (Faktorisierung einer Zahl) viel länger dauert als die Multiplikation, oder genauer gesagt, dass auf einem klassischen Computer keine Methode zur Faktorisierung großer Zahlen in Polynomzeit gefunden wurde, obwohl dies nicht der Fall war Es ist bewiesen, dass ein solcher Algorithmus nicht existieren kann.

In RSA gibt es wie in jedem anderen kryptografischen System mit einem öffentlichen Schlüssel zwei Schlüssel: öffentlich und privat. Der RSA-Algorithmus nimmt eine durch eine Bitkette dargestellte Eingangsnachricht und wendet eine mathematische Operation darauf an (Erhöhen einer großen Zahl auf ein Potenzmodul), um ein Ergebnis zu erhalten, das nicht vom Zufall unterscheidbar ist. Zur Entschlüsselung wird das Ergebnis genommen und ein ähnlicher Vorgang ausgeführt, um die ursprüngliche Nachricht zu empfangen. Bei der asymmetrischen Kryptographie wird die Verschlüsselung mit einem öffentlichen Schlüssel und die Entschlüsselung mit einem privaten Schlüssel durchgeführt.

Wie ist das möglich? Aufgrund der Tatsache, dass die verwendeten Werte zu einer endlichen zyklischen Gruppe gehören (die Menge der Ganzzahlen mit Multiplikation in modularer Arithmetik). Computer funktionieren nicht sehr gut mit willkürlich großen Zahlen, aber die Eigenschaft der zyklischen Gruppe lautet "umbrechen" - eine Zahl, die größer als das zulässige Maximum ist, wird auf einen Wert aus der zulässigen Menge "umbrochen". Dies ermöglicht es uns, Schlüssel mit einer Länge von "nicht mehr als" einer bestimmten Anzahl von Bits zu verwenden. In der Kryptographie, die auf elliptischen Kurven basiert, werden auch zyklische (multiplikative) Gruppen verwendet, die jedoch etwas anders aufgebaut sind, wie wir später sehen werden.

Auf einer sehr primitiven Ebene benötigt RSA lediglich zwei große Primzahlen, die multipliziert werden, um das sogenannte Modul zu erhalten. Alle anderen Zahlen, mit denen Operationen ausgeführt werden, sollten zwischen Null und dem Modulwert liegen. Das Modul selbst wird Teil des öffentlichen Schlüssels - seine Länge bestimmt die Länge des Schlüssels. Der zweite Teil des öffentlichen Schlüssels ist die Zahl zwischen Null und dem Wert der Euler-Funktion (moderne RSA-Implementierungen verwenden die Carmichael-Funktion anstelle von Euler) aus dem Modul, mit einigen zusätzlichen Einschränkungen. Schließlich können Sie den privaten Schlüssel berechnen, indem Sie die modulare Gleichung lösen. Um die Nachricht zu verschlüsseln, nehmen wir die Nummer, die die Nachricht darstellt, und erhöhen sie einfach auf die Potenz, die dem Wert des öffentlichen Schlüssels entspricht. Um sie zu entschlüsseln - um die ursprüngliche Nachricht zu erhalten, erhöhen Sie sie auf die Potenz, die dem Wert des privaten Schlüssels entspricht. Aufgrund der zyklischen Natur der Gruppe erhalten wir die gleiche Bedeutung.

Heute hat RSA zwei Hauptprobleme, von denen eines eine Konsequenz des anderen ist. Mit zunehmender Schlüssellänge wächst die Komplexität nicht so schnell, wie wir es uns wünschen. Dies liegt daran, dass es einen subexponentiellen (aber immer noch superpolynomiellen ) Faktorisierungsalgorithmus gibt. Daher sollte die Länge des RSA-Schlüssels etwas schneller wachsen als die des ECC-Schlüssels, um das erforderliche Schutzniveau aufrechtzuerhalten. Aus diesem Grund sind die heute gebräuchlichsten RSA-Schlüssellängen recht groß: 2048 und 3072 Bit.

Wenig später werden wir anhand konkreter Zahlen sehen, wie sich die Schlüssellänge auf die endgültige Leistung des Kryptosystems auswirkt, indem wir die von Let's Encrypt RSA und ECDSA signierten Zertifikate vergleichen.

E lliptic C urve Digital S ignature A- Algorithmen

Auf der Suche nach zuverlässigeren Funktionen mit einer geheimen Eingabe setzten Kryptografen Mitte der 80er Jahre einen Zweig der Mathematik ein, der elliptischen Kurven gewidmet war.

Es wäre zu schwierig, alle Details der Kryptographie auf der Grundlage elliptischer Kurven in einem Text zu beschreiben, daher werden wir dies nicht tun. Betrachten wir stattdessen eine Einwegfunktion mit einer geheimen Eingabe, die auf elliptischen Kurven und dem diskreten Logarithmusproblem basiert.

Es gibt eine Vielzahl von Rezensionsmaterialien und detailliertere Einführungen in diesen Bereich der Kryptographie. Wir möchten auf „ECC: eine sanfte Einführung“ von Andrea Corbellini hinweisen, insbesondere wenn Sie sich für das Gerät interessieren.

Wir in diesem Material sind an einer viel einfacheren Erklärung interessiert.
Eine elliptische Kurve wird durch eine Gleichung definiert, die wie folgt aussieht:

y^{2} = x^{3} + a x + b

$y ^ 2 = x ^ 3 + ax + b$ .

Das zweite Objekt ist eine zyklische Untergruppe über einem endlichen Feld. Die folgenden Parameter werden im ECC-Algorithmus verwendet:

Primzahl $p$ , welches die Dimension des Endfeldes bestimmt;
Gewinnchancen $a$ und $b$ elliptische Kurvengleichungen;
Basispunkt $G$ Erzeugen der bereits erwähnten Untergruppe;
Auftrag $n$ Untergruppen;
Cofaktor $h$ Untergruppen.

Infolgedessen wird der Parametersatz für unsere Algorithmen durch sechs dargestellt

$(p, a, b, G, n, h)$ .

Punkte einer elliptischen Kurve gehören zu einem endlichen Feld

m a t h b b F_{p}

$\ mathbb {F} _p$ wo

p

$p$ Dies ist eine ziemlich große Primzahl. Wir haben also viele ganze Zahlen modulo

p

$p$ Wo Operationen wie Addition, Subtraktion, Multiplikation und umgekehrt möglich sind. Addition und Multiplikation funktionieren auf ähnliche Weise wie wir dies in Bezug auf die modulare Arithmetik des RSA-Abschnitts (Wrap-Around) beschrieben haben.

Da die Kurve für jeden Punkt symmetrisch zur x-Achse ist

P

$P$ wir können nehmen

- P

$−P$ und den Punkt gegenüber bekommen. Wir vereinbaren sofort, dass der Punkt

- O

$−O$ entspricht Null, d.h.

- O

$−O$ wird einfach sein

O

$O$ .

Das Hinzufügen von Punkten auf einer Kurve wird so definiert, dass die Punkte bekannt sind

P

$P$ und

Q

$Q$ können wir eine Linie durch diese beiden Punkte ziehen, sowie eine dritte -

R

$R$ so das

P + Q = - R

$P + Q = -R$ und

P + Q + R = 0

$P + Q + R = 0$ .

Werfen wir einen Blick auf Mark Hughes ' illustrierte Illustration:

Wir sehen eine gerade Linie entlang der Oberfläche des Torus. Die Linie schneidet zwei zufällig ausgewählte Punkte auf der Kurve.

Um zu finden $R$ Wir ziehen eine Linie vom ersten ausgewählten Punkt $P$ zum zweiten $Q$ Setzen Sie die Linie fort, bis sie die Kurve am dritten Punkt kreuzt $-R$ .

Reflektieren Sie nach dem Schnittpunkt den Punkt relativ zur Abszissenachse, um den Punkt zu finden $R$ .

Die Multiplikation mit einem Skalar wird ganz offensichtlich bestimmt:

n c d o t P = P + P + P + d o t s + P

$n \ cdot P = P + P + P + \ dots + P$ .

Die Einwegfunktion mit einer geheimen Eingabe beruht in diesem Fall auf dem diskreten Logarithmusproblem für elliptische Kurven und nicht auf der Faktorisierung, wie dies bei RSA der Fall ist. Das diskrete Logarithmusproblem ist in diesem Fall wie folgt formuliert: falls bekannt

P

$P$ und

Q

$Q$ , dann wie zu finden

k

$k$ so dass

Q = k c d o t P

$Q = k \ cdot P$ ?

Sowohl das Faktorisierungsproblem (zugrunde liegende RSA) als auch der diskrete Logarithmus für elliptische Kurven (die Grundlage von ECDSA und ECDH sind) werden als schwierig angesehen. Mit anderen Worten, es gibt keine Algorithmen, um diese Probleme in der Polynomzeit für eine bestimmte Schlüssellänge zu lösen.

Obwohl ich normalerweise mit schmutzigen (bestenfalls) Lumpen bombardiert werde, um Signaturverteilungsalgorithmen (ECDH) mit Signatur (ECDSA) zu mischen, muss ich noch erklären, wie sie zusammenarbeiten.Ein modernes TLS-Zertifikat enthält in unserem Fall einen öffentlichen Schlüssel aus einem Paar, das mit einem Algorithmus generiert wurde, der auf elliptischen Kurven basiert, die normalerweise von einer autorisierenden Organisation signiert wurden. Der Client überprüft die Serversignatur und generiert ein gemeinsames Geheimnis. Dieses Geheimnis wird in einem symmetrischen Verschlüsselungsalgorithmus wie AES oder ChaCha20 verwendet. Die Grundprinzipien bleiben jedoch dieselben: Vereinbaren Sie einen Satz (sechs) von Parametern, und erhalten Sie ein Schlüsselpaar, wobei der private Schlüssel eine zufällig ausgewählte Ganzzahl ist (ein Faktor von

Q = k \cdot P

$Q=k\cdot P$

G

$G$

n

$n$ (

n

$n$

n \cdot G = 0

$n\cdot G=0$

(EC) DH (E) + ECDSA = Moderne Form des Handshakes

In der modernen TLS-Version 1.3 generieren Client und Server im laufenden Betrieb ein Schlüsselpaar, um eine Verbindung herzustellen. Dies wird als "kurzlebige" Version des Schlüsselaustauschalgorithmus bezeichnet. Die beliebtesten TLS-Bibliotheken unterstützen genau eine solche Protokollversion. Zum größten Teil wird heute die von Daniel Bernstein Jr. (djb) vorgeschlagene elliptische Edwards- Kurve 25519 verwendet , die einen 128-Bit-Schutz bietet. Seit 2014 steht diese Kurve zum Erstellen von Schlüsselpaaren in der openssh-Bibliothek zur Verfügung. Bis Ende 2019 richten Browser jedoch noch keine TLS-Sitzung mit Servern ein, die den öffentlichen Schlüssel für den EdDSA-Signaturalgorithmus verwenden.

Schauen wir uns an, wie alles in TLS 1.3 funktioniert.

In der neuesten Version des Protokolls sind die Schlüsselverteilungsmechanismen auf (EC) DH (E) beschränkt - x25519 ist die häufigste Funktion zum Abrufen eines freigegebenen Schlüssels - sie wird von den meisten Browser- und Server-TLS-Bibliotheken unterstützt. Die Verschlüsselungssuite besteht nur aus drei Einträgen: TLS_AES_128_GCM_SHA256, TLS_AES_256_GCM_SHA384 und TLS_CHACHA20_POLY1305_SHA256. Für diejenigen unter Ihnen, die wissen, wie die Chiffresuiten in der vorherigen Version des Protokolls - TLS 1.2 - benannt wurden, ist es offensichtlich, dass die Angabe des Schlüsselaustauschmechanismus während des Übergangs zu TLS 1.3 von der Chiffresuite „getrennt“ wurde. Außerdem wurden statische RSA- und DH-Schlüsselaustauschmethoden aus der Spezifikation gestrichen. Auch die Sitzungswiederherstellung in TLS 1.3 mit Hilfe von PSK und Tickets der vorherigen Sitzung erfolgt nach dem ECDHE-Protokoll, wobei die letzte E-Ephemeralität besonders wichtig ist.Außerdem ist es in TLS 1.3 nicht möglich, eigene Werte für den Diffie-Hellman-Mechanismus festzulegen. In den Protokollspezifikationen ist nur noch ein vordefinierter Satz enthalten. In Bezug auf die Sicherheit dieses Satzes besteht Konsens.

Von besonderem Interesse ist die Tatsache, dass moderne asymmetrische Verschlüsselungsmechanismen unterschiedlich arbeiten. In der ECC (insbesondere bei Verwendung von ECDSA-Zertifikaten) verwenden wir im Vergleich zu RSA relativ kurze Schlüssel, um ein akzeptables Sicherheitsniveau zu erreichen. Auf diese Weise können Sie starke asymmetrische Kryptografie- und Schlüsselaustauschschemata auch auf Geräten verwenden, die anscheinend nicht über genügend Strom für die erforderlichen Vorgänge verfügen sollten, z. B. Smartcards.

Zunächst ist zu klären, was der Begriff „hybrides Kryptosystem“ für die Beschreibung von TLS 1.3 bedeutet. Das hybride Kryptosystem verwendet ein asymmetrisches Verschlüsselungsschema (mit einem öffentlichen Schlüssel), um ein gemeinsames Geheimnis zu erstellen, das dann als Schlüssel in einem symmetrischen Block- oder Stream-Verschlüsselungsalgorithmus verwendet wird.

Zweitens gibt es eine Infrastruktur aus öffentlichen Schlüsseln (PKI) und Zertifikaten (CA). Es ist interessant, dass Martin Hellman im Jahr 2004 eine der „unbesungenen Helden“ - Lauren Könfelder - erwähnte, deren These zur Verteidigung des MIT-Bachelor-Diploms darin bestand, eine Baumstruktur zu schaffen - was wir heute als PKI kennen. Aber kommen wir zurück zu den Zertifikaten.

Die Tatsache, dass der Server den privaten Schlüssel wirklich besitzt, wird durch seine Signatur verifiziert, die mit dem öffentlichen Schlüssel verifiziert werden kann. Die Zertifikatdatei auf dem Server bestätigt, dass ein bestimmter öffentlicher Schlüssel zu einem bestimmten Server gehört. Dies bedeutet, dass Sie eine sichere Verbindung mit dem gewünschten Gesprächspartner herstellen und kein Betrüger - Ihre Bank, kein Cyber-Betrug.

TLS 1.3 hat das Verhandlungsschema im Vergleich zu früheren Versionen des Protokolls erheblich verbessert. Jetzt signiert der Server alle Informationen, die zum Zeitpunkt der Erstellung einer solchen Signatur im Handshake eingegangen sind: Client-Hallo und sein eigener Server-Hallo zusammen mit den für die Verwendung ausgewählten Chiffren. Schauen wir uns den entsprechenden Abschnitt der Interaktionsbeschreibung aus RFC 8446 an :

Client Server Key ^ ClientHello Exch | + key_share* | + signature_algorithms* | + psk_key_exchange_modes* v + pre_shared_key* --------> ServerHello ^ Key + key_share* | Exch + pre_shared_key* v {EncryptedExtensions} ^ Server {CertificateRequest*} v Params {Certificate*} ^ {CertificateVerify*} | Auth {Finished} v <-------- [Application Data*] ^ {Certificate*} Auth | {CertificateVerify*} v {Finished} --------> [Application Data] <-------> [Application Data]

In TLS 1.3 sendet der Client seinen Teil des Schlüssels (zusammen mit den erforderlichen Parametern) und die Liste der in der ersten Nachricht verfügbaren Signaturen (Client Hello). Die zu diesem Zeitpunkt erforderlichen Schlüssel werden vom Kunden im laufenden Betrieb erstellt - der Benutzer bemerkt dies nicht einmal. Als Nächstes tauschen Client und Server diese Informationen aus, um ein gemeinsames Geheimnis zu erstellen - einen Sitzungsschlüssel, der aus dem Pre-Master-Paar erstellt (oder genauer abgeleitet) wird, das empfangen wird, nachdem der Server dem Client mit seiner Nachricht geantwortet hat (Server Hello).
Auf der Seite „Server Hello“ sehen Sie den Datensatz, der der Übertragung des Zertifikats an den Client (Certificate *) entspricht, zusammen mit der CertificateVerify * -Prüfung, die bestätigt, dass der Teilnehmer wirklich einen privaten Schlüssel in Bezug auf den entsprechenden öffentlichen Schlüsseldatensatz hat. Anschließend wird ein (symmetrisches) Sitzungsschlüsselpaar erstellt Erfolgsfall. Mit anderen Worten, der datenanfragende Teilnehmer (Client) hat die Authentizität des antwortenden Teilnehmers (Servers) erfolgreich überprüft, indem er zur Verwendung eines gemeinsamen Geheimnisses übergegangen ist.

Die beiden wichtigsten kryptografischen Vorgänge werden bei dieser Übertragung geschützt: Erstellen einer Signatur und Überprüfen der Signatur. Diese Vorgänge werden normalerweise an verschiedenen Enden der Verbindung ausgeführt, da Clients meistens die Authentizität des Servers überprüfen. Die Signatur ist im Wesentlichen eine Bestätigung des Besitzes des privaten Schlüssels, der dem öffentlichen Schlüssel entspricht. Das heißt, wir erhalten Daten vom Unterzeichner und stellen sicher, dass die Nachricht während der Übertragung nicht geändert wurde.

Bei Verwendung des RSA-Algorithmus ist die Erstellung einer Signatur am teuersten, wie wir später anhand der Zahlen zeigen werden. Da wir mit einem 2048- oder 3072-Bit-Schlüssel signieren, wird der Server durch eine solche Operation erheblich belastet - viel stärker als der Client bei der (Signatur-) Überprüfung.

In ECDSA arbeiten wir mit relativ kurzen Schlüsseln (im Benchmark-Beispiel betrachten wir ECDSA anhand der NIST P-256-Kurve (oder secp256v1), diese Schlüssel sind jedoch mit komplexeren Vorgängen verbunden. Infolgedessen kann die Verwendung von ECC als „invertierter“ RSA mit dargestellt werden Leistungsgesichtspunkte: Der Client ist mit der Signaturprüfungsoperation viel schwerer belastet, während der Server die Signaturerstellungsoperation einfach handhabt, wie die Messungen im Benchmark-Abschnitt belegen.

Dieser Effekt hilft bei der Skalierung des Internets - da moderne Clients fast so leistungsfähig sind wie Server (wenn wir nur die Taktrate des Prozessorkerns berücksichtigen), können sie problemlos einen rechenschweren Betrieb aufnehmen. Der Server kann seinerseits die freiwerdende Rechenleistung nutzen, um mehr Signaturen zu erstellen und dadurch mehr Sitzungen einzurichten.

Zertifikatsignatur bei Let's Encrypt

Wir werden unseren Lesern eine einfache und verständliche Anleitung zur Verfügung stellen, auf der Sie mithilfe eines ECDSA-Schlüsselpaares, in dem Let's Encrypt öffentlich signiert und als Zertifikat in der Vertrauenszertifikatskette enthalten ist, unabhängig einen Server erstellen können, mit dem eine TLS-Sitzung aufgebaut werden kann.
Wir haben uns entschlossen, den vollständigen Pfad vom Erstellen von Schlüsseln über das Erstellen einer Zertifikatsignierungsanforderung (Certificate Signing Request, CSR) für Let's Encrypt bis hin zum Senden zur Signatur mit dem Dienstprogramm certbot anzuzeigen, das die erforderlichen Ketten und das ECDSA-Zertifikat selbst zurückgibt.

Zuerst müssen Sie ein Schlüsselpaar erstellen. Dafür verwenden wir die OpenSSL-Bibliothek. Das OpenSSL-Benutzerhandbuch besagt, dass das Erstellen von Schlüsseln für Algorithmen auf der Basis von elliptischen Kurven mit einem speziellen Befehl erfolgt, der der Familie von Algorithmen auf der Basis von elliptischen Kurven gewidmet ist.

 openssl ecparam -genkey -name -secp256v1 -out privatekey.pem

Um zu überprüfen, ob unser Team ordnungsgemäß funktioniert hat, führen wir den Befehl ec aus, der den Pfad zu der neu erstellten Datei mit dem privaten Schlüssel angibt.

 openssl ec -in privatekey.pem -noout -text

Die Ausgabe sollte uns die verwendete Kurve zeigen, mit der der Schlüssel erzeugt wurde.

Der nächste Schritt ist bei der Erstellung eines CSR sehr wichtig. Um nicht jedes Mal den zum Signieren eines Zertifikats erforderlichen Fragebogen auszufüllen, benötigen wir eine Konfigurationsdatei. Glücklicherweise wurde fast die gesamte Arbeit für uns von Mozilla erledigt und der „ SSL-Konfigurationsgenerator “ erstellt. Darin können Sie aus einer Vielzahl von Optionen für Servermodi auswählen, mit denen Sie eine TLS-Verbindung herstellen können. Die saubere OpenSSL-Konfiguration, die aus irgendeinem Grund im Mozilla-Generator fehlt, sieht folgendermaßen aus:

 [ req ] prompt = no encrypt_key = no default_md = sha256 distinguished_name = dname req_extensions = reqext [ dname ] CN = example.com emailAddress = admin@example.com [ reqext ] subjectAltName = DNS:example.com, DNS:*.example.com

Hinweis: Sie müssen keine Konfigurationsdatei haben - wenn diese nicht vorhanden ist, werden Sie aufgefordert, alle Felder in der Befehlszeile auszufüllen. Mit der Konfigurationsdatei, deren Pfad wir im nächsten Befehl angeben, wird der Vorgang vereinfacht.

Als Nächstes wird die Zertifikatsignierungsanforderung (Certificate Signing Request, CSR) selbst erstellt. Dafür haben wir ein praktisches OpenSSL-Team.

 openssl req -new -config -pathtoconfigfile.cnf -key privatekey.pem -out csr.pem

Wir können auch die Richtigkeit der neu erstellten CSR überprüfen.

 openssl req -in csr.pem -noout -text -verify

Schließlich kommen wir zur letzten Stufe - mit dem ACME-Client certbot werden wir unsere Anfrage zum Signieren des Organisationszertifikats Let's Encrypt weiterleiten.

Certbot hilft Ihnen nicht nur, ein Zertifikat zu erhalten, sondern bietet auch viele andere großartige Optionen. Wir fügen hinzu, dass es besser ist, die Option --dry-run bevor Sie versuchen, ein echtes Zertifikat für eine Ihrer Domänen zu erhalten, wenn Sie neu in der Kryptografie mit einem öffentlichen Schlüssel sind und die derzeit vorhandene Infrastruktur für öffentliche Schlüssel nicht wirklich verstehen.

 certbot certonly --dry-run --dns-somednsprovider --domain “example.com” --domain “*.example.com” --csr csr.pem

In diesem Fall überprüft der Certbot-Client, ob die in der Befehlszeile angeforderte Liste der erforderlichen Domänen mit der Liste in der Zertifikatsignierungsanforderung (Certificate Signing Request, CSR) übereinstimmt. In der --dns-somednsprovider wir --dns-somednsprovider bisschen --dns-somednsprovider , da es viele Möglichkeiten gibt, Let's Encrypt zu bestätigen, dass Sie einen bestimmten Teil des Internetverkehrs besitzen. Wenn Sie jedoch einen Cloud-Anbieter wie DigitalOcean, AWS, Azure oder Hetzner verwenden, haben Sie möglicherweise bereits eine einfachere Möglichkeit, die für die Zertifizierung erforderlichen Informationen bereitzustellen, da sich Ihr Anbieter um das Integrationstool gekümmert hat.

Wenn Sie sicher sind, dass die mit dem certbot für Let's Encrypt an den CSR übergebenen Parameter korrekt sind, entfernen --dry-run einfach den Parameter --dry-run aus dem Befehl und fahren Sie fort.

Im Erfolgsfall sendet der Client mehrere Zertifikate zurück: das signierte Zertifikat selbst, das Zwischenzertifikat und das Stammzertifikat sowie eine Kombination dieser Zertifikate in Form einer Zertifikatskette im PEM-Format.

OpenSSL hat einen Befehl, mit dem wir in das Zertifikat schauen:

 openssl x509 -in chainfilepath.pem -noout -text

Es sollte nun klar sein, dass Let's Encrypt das Zertifikat mit dem SHA256-Hash-Algorithmus signiert hat. Darüber hinaus plant Let's Encrypt nur das Hinzufügen von Stamm- und Zwischensignaturen zu ECDSA. Daher muss es sich vorerst noch mit RSA-Zwischensignaturen begnügen. Es ist jedoch nicht beängstigend, da Sie in jedem Fall den öffentlichen ECDSA-Schlüssel verwenden.

Am Ende dieses Abschnitts möchten wir einige Informationen zum Vergleich der Schlüssellängen verschiedener Algorithmen hinzufügen. In der Informationssicherheit ist es üblich zu sagen, dass die Sicherheitsstufe 2 ^ x ist, wobei x die Bitlänge ist (RSA ist eine Ausnahme, da es etwas langsamer wächst als der Exponent). Informationen zum Vergleich der Schlüssel verschiedener Algorithmen finden Sie auf der OpenSSL-Wiki- Seite:

Symmetrische Schlüssellänge	RSA-Schlüssellänge	Elliptic Curve Key Length
80	1024	160
112	2048	224
128	3072	256
192	7680	384
256	15360	512

Wie Sie sehen, sind die Unterschiede spürbar. Derzeit können Sie mit Let's Encrypt nur signierte Zertifikate auf den Schlüsseln von nur zwei elliptischen Kurven empfangen - 256 (secp256v1) und 384 (secp384r1).

Bekannte Schwierigkeiten ebenso wie die NSA

Gepostet von: xkcd

Das zentrale Problem bei der Verwendung von Kryptographie auf der Basis elliptischer Kurven war möglicherweise die Notwendigkeit eines sehr sauber implementierten Zufallszahlengenerators, der zum Erstellen von Schlüsseln einer bestimmten Sicherheitsstufe erforderlich ist.

Mit dem Dual_EC_DRBG- Algorithmus war ein großer Skandal verbunden - die Lösung dauerte viele Jahre. Es besteht Unsicherheit über die Patentgrundlage rund um ECC - es ist bekannt, dass viele Patente Certicom gehörten, das von Blackberry erworben wurde. Es gibt auch mehrere bekannte Fälle der Blackberry ECC-Zertifizierung. Schließlich gibt es ein gewisses Misstrauen gegenüber den NIST-Standards, das von der NSA oder einem anderen US-Geheimdienst beeinflusst werden könnte.

Fehler bei der Implementierung kryptografischer Standards sind ein völlig orthogonales Thema. Im Jahr 2010 litt die PlayStation 3 unter einem Verlust des privaten Schlüssels von Sony aufgrund einer falschen Implementierung des ECDSA-Algorithmus - Sony konnte mit dem RNG nicht umgehen und gab dieselbe Zufallszahl an, wodurch es möglich wurde, die Funktion mit einer geheimen Eingabe zu lösen. OpenSSL litt im folgenden Jahr darunter, behebte jedoch schnell eine Sicherheitslücke, die es ihm ermöglichte, einen privaten Schlüssel mithilfe eines Zeitangriffs zu erhalten - weitere Details finden Sie in der Original-Forschungsveröffentlichung .

Auf einer RSA-Konferenz im Jahr 2013 präsentierte eine Gruppe von Forschern ein Forschungspapier mit dem Titel „ Randomly Failed! Speziell für Sicherheitslücken der SecureRandom-Java-Klasse. Sechs Monate später begannen die Dinge mit Bitcoin-Geldbörsen, die mit einem kryptografisch unsicheren Pseudozufallszahlengenerator erstellt wurden.

Aufgrund der Tatsache, dass im August 2013 mehrere schwerwiegende Sicherheitslücken in kurzer Zeit entdeckt wurden, veröffentlichte die IETF RFC 6979 , in dem die deterministische Generierung von k beim Erstellen eines Schlüssels beschrieben wird. Wir könnten schreiben, dass das Problem auf diese Weise gelöst wurde, aber wir werden es nicht tun - zu jedem Zeitpunkt können Forscher aufgrund unnötiger Abweichungen von den Protokollspezifikationen neue Fehler in der Implementierung finden.

Und ein paar Worte zur NSA. Wenn Sie die Geschichte von Dual_EC_DRBG nicht kennen - nehmen Sie sich etwas Zeit und lesen Sie die relevanten Materialien. Sie werden es nicht bereuen, dass Sie die Details herausgefunden haben. Edward Snowden wurde ein Teil dieser Geschichte, weil aufgrund seiner undichten Stellen im Jahr 2013 alle Zweifel, die bestanden, bestätigt wurden. Dies führte dazu, dass viele namhafte Kryptografen das Vertrauen in NIST verloren, da diese Organisation viele der in ECDSA funktionierenden elliptischen Kurven und Algorithmen erstellte und beschrieb.

Die von Daniel Burnshite verfasste Kurve 25519 und die Diffie-Hellman-Funktion für die Schlüsselverteilung sind die Antwort auf viele der oben genannten Fragen. Und wie wir bereits geschrieben haben, gibt es eine stetige Bewegung in Richtung EdDSA. Bei den NIST-Kurven wurde noch keine Bestätigung für ihre Verwundbarkeit gefunden, und die Erfahrung mit Zufallszahlen war ziemlich schmerzhaft und trug zur raschen Assimilation bei.

Abschließend möchten wir John von Neumann zitieren: "Wer eine Schwäche für arithmetische Methoden zur Gewinnung von Zufallszahlen hat, ist zweifelsfrei sündlos."

Einige Benchmarks

Wir haben den NGINX 1.16.0-Server mit der OpenSSL-Bibliothek Version 1.1.1d verwendet, um Tests mit zwei Zertifikaten durchzuführen. Wie bereits erwähnt, können Sie in Let's Encrypt derzeit nur die Algorithmen prime256v1 und secp384r1 verwenden, um eine Zertifikatsignierungsanforderung zu erstellen, und Root- und Intermediate-Zertifikate nicht mit einer ECDSA-Signatur versehen. Möglicherweise wird diese Funktion behandelt, während Sie diesen Hinweis lesen.

Signaturtyp	Handshakes pro Sekunde
ECDSA (prime256v1 / nistp256)	3358.6
RSA 2048	972,5

Wie Sie sehen, beträgt der Gesamtunterschied zwischen der ECDSA-Leistung und dem allgemein akzeptierten RSA mit einer Schlüssellänge von 2048 Bit auf einem einzelnen Kern der Intel® Xeon® Silver 4114-CPU bei 2,20 GHz (Veröffentlichung im dritten Quartal 17) das 3,5-fache.

Sehen wir uns die Ergebnisse der Ausführung des Befehls openssl -speed für ECDSA und RSA auf demselben Prozessor an.

Signaturtyp	unterschreiben	verifizieren	Vorzeichen / Sek	verifizieren / Sek
RSA 2048 Bit	717 μs	20,2 μs	1393.9	49458.2
256-Bit-ECDSA (nistp256)	25,7 μs	81,8 μs	38971.6	12227.1

Hier finden wir eine Bestätigung einer zuvor verfassten Arbeit darüber, wie sich die Rechenoperationen einer Signatur und ihre Überprüfung zwischen ECC und RSA unterscheiden. Gegenwärtig ist die Kryptografie mit TLS 1.3 auf der Basis elliptischer Kurven ausgestattet, wodurch die Serverleistung erheblich gesteigert wird und das Schutzniveau im Vergleich zu RSA erhöht wird. Dies ist der Hauptgrund, warum wir von Qrator Labs Kunden, die bereit sind, auch ECDSA-Zertifikate zu verwenden, empfehlen und nachdrücklich empfehlen. Bei modernen CPUs beträgt der Leistungsgewinn zugunsten von ECDSA das Fünffache.

Wenn Sie daran interessiert sind, wie Ihr (Heim- oder Server-) Prozessor mit kryptografischem Computing umgeht, führen Sie den Befehl openssl speed aus. Mit den -eddsa -rsa , -ecdsa und -eddsa Sie die für das Benchmarking interessanten Algorithmen angeben.

Die Zukunft (in Überlagerung)

Ironischerweise kündigte Google beim Schreiben dieses Materials an, "Quantenüberlegenheit zu erreichen". Bedeutet dies, dass wir bereits in Gefahr sind und alle Fortschritte, die bis zum gegenwärtigen Zeitpunkt erzielt wurden, keine Geheimhaltung mehr gewährleisten können?

Nein.

Wie Bruce Schneier in dem Aufsatz „Kryptographie nach der Landung von Außerirdischen“ für das IEEE-Rundschreiben über Sicherheit und Datenschutz schrieb, kann ein Quantencomputer nur der asymmetrischen Kryptographie mit einem öffentlichen Schlüssel einen schweren Schlag versetzen. Symmetrische Algorithmen bleiben erhalten.

Aber um fortzufahren, werden wir Herrn Schneier selbst das Wort erteilen:

Es gibt ein weiteres zukünftiges Szenario, für das kein Quantencomputer erforderlich ist. Während wir jetzt mehrere mathematische Theorien haben, die der Einseitigkeit in der Kryptographie zugrunde liegen, ist der Beweis der Gültigkeit dieser Theorien tatsächlich eines der größten offenen Probleme in der Informatik. Genauso wie ein intelligenter Kryptograf einen neuen Trick finden kann, der das Hacken eines bestimmten Algorithmus erleichtert, können wir uns Aliens mit einer ausreichenden mathematischen Theorie vorstellen, um alle Verschlüsselungsalgorithmen zu knacken. Heute scheint es lächerlich. Die Kryptographie mit öffentlichen Schlüsseln ist eine Zahlentheorie und potenziell anfällig für mathematisch denkende Aliens. Symmetrische Kryptografie ist so nichtlinear, so einfach zu erstellen und zu komplizieren und auch wie einfach es ist, Schlüssel zu verlängern, was für eine Zukunft unvorstellbar ist. Ein Beispiel ist die AES-Variante mit einer Block- und Schlüsselgröße von 512 Bit sowie 128 Runden. Wenn sich Mathematik nicht grundlegend von unserem derzeitigen Verständnis unterscheidet, ist ein solcher Algorithmus sicher, bis Computer aus etwas anderem als Materie bestehen und etwas anderes als Raum einnehmen.

Aber wenn das Unvorstellbare passiert, bleibt uns nur eine Kryptographie übrig, die ausschließlich auf der Informationstheorie basiert: Einweg-Chiffriernotizblöcke und ihre Varianten.

Bruce Schneier beschreibt perfekt den Bereich, in dem neben Implementierungsfehlern die Hauptschwachstellen der modernen Kryptographie liegen. Wenn es irgendwo eine Gruppe wohlhabender Mathematiker, Kryptoanalytiker und Kryptographen gibt, die zusammen mit Computeringenieuren an dem Beweis oder der Widerlegung einiger besonders komplexer mathematischer Probleme (wie P? = NP) arbeiten und es gerade geschafft haben, einige Fortschritte in dieser Aktivität zu erzielen - Unsere Position ist verwundbar. Wenn man Verschwörungstheorien ablehnt, kann man sagen, dass ein solcher Fortschritt in den Bereichen Informatik, Informationstheorie und Berechenbarkeitstheorie kaum verborgen werden kann. Ein solches Ereignis hätte die Namen ihrer eigenen Schöpfer auf den Seiten der Geschichte und insbesondere in den Lehrbüchern der Internetgeschichte eingetragen, die für jede so intelligente Person oder Gruppe von unschätzbarem Wert sind. Ein ähnliches Szenario kann daher als unmöglich verworfen werden.

Es ist auch unklar, ob solche Erfolge im Quantencomputing in den nächsten 5 Jahren erzielt werden - und es gibt bereits kryptografische Primitive, die für die Verwendung in der postquantalen Welt geeignet sind: Gitter, die die supersinguläre Isogenisierung elliptischer Kurven verwenden, Hash-Funktionen, Fehlerkorrekturcodes. Jetzt experimentieren Sicherheitsexperten nur noch mit ihnen, aber es besteht kein Zweifel daran, dass die Menschheit bei Bedarf einen Weg finden wird, neue Algorithmen in jeder Größenordnung schnell einzusetzen.

Es muss nur hinzugefügt werden, dass die auf elliptischen Kurven basierende Kryptografie für das nächste Jahrzehnt ideal für die Ziele und Bedürfnisse geeignet zu sein scheint, die sich die meisten Benutzer selbst gesetzt haben, um Sicherheit und hohe Leistung zu bieten.

Funktionsweise der Kryptographie mit elliptischen Kurven in TLS 1.3