Der Tetris-Druckeralgorithmus wandelt eine vorgegebene Folge von Formen um, ordnet sie neu und senkt sie nach unten. Dabei werden mithilfe der Tetris-Mechanik beliebige Bitmaps generiert.
Beschreibung des Algorithmus
Der Algorithmus konvertiert die Pixel des
Quellbildes zeilenweise in die Quadrate des
Tetris- Feldes und bewegt sich von unten nach oben. Um ein einzelnes Quadrat zu erzeugen, setzt der Algorithmus eine Struktur zusammen, die aus einem rechteckigen Bereich besteht, der vollständig von einem Quadrat darunter unterstützt wird. Nachdem der Zusammenbau des rechteckigen Bereichs abgeschlossen ist, werden seine Linien gelöscht, wobei ein Quadrat darunter verbleibt. Hier sind drei Beispiele für dieses Verhalten.
Wie unten gezeigt, kann der Algorithmus auch mehrere Quadrate mit einer Struktur erzeugen.
Bei der Erstellung einer Reihe müssen alle auf diese Weise erstellten Quadrate auf etwas basieren. In den oben gezeigten Bildern befinden sich die erzeugten Quadrate auf dem Boden des Spielfelds. Wenn jedoch eine beliebige Linie Löcher enthält, kann sie nicht die Unterstützung bieten, die zum Erstellen einer Linie darüber erforderlich ist. Der Algorithmus löst dieses Problem, indem er eine flache Plattform mit Löchern auf der Saite erstellt. In der Animation unten besteht eine Plattform, die auf einer Linie aufgebaut ist, aus einem roten Quadrat. Eine Plattform ist eine temporäre Struktur, die durch Einfügen der letzten Form entfernt wird.

Die unten gezeigte Reihe von 5 roten Quadraten befindet sich über der Reihe von 3 roten Quadraten. Dies wird durch den Bau einer flachen Plattform über dem Endergebnis erreicht. Die Plattform bietet die notwendige Unterstützung, um 5 rote Quadrate zu generieren. Am Ende wird die Plattform durch Einfügen der letzten Form gelöscht und die neue Linie wird eingefügt. Beachten Sie, dass die Plattform nicht benötigt wird, wenn der Algorithmus Linien in umgekehrter Reihenfolge erzeugen muss (eine Linie aus 3 roten Quadraten über einer Linie aus 5 roten Quadraten).
Ein Quadrat Muster
Als Referenz gebe ich die Namen von 7 Tetramino (Spielfiguren) an.
Die in diesem Artikel vorgestellte Version von Tetris Printer Algorithm wurde speziell für das Rendern von Sprites aus alten Videospielen entwickelt. Diese Spiele packten Grafiken in 8 × 8 Kacheln, und jedem Pixel wurden 2 Bytes zugewiesen. Daher enthielten Sprites normalerweise nur 3 Farben plus transparente Bereiche und hatten meist eine Größe von 16 × 16 oder 16 × 32 Pixel.
Die Animation unten zeigt alle Muster, die zum Erstellen einzelner Quadrate verwendet werden. Jedes Muster verwendet austauschbare Tetramino J, T und L, wodurch am unteren Rand ein einzelnes Quadrat entsteht. Der Algorithmus weist dieses Tetramino einer der drei im Sprite vorhandenen Farben zu. Dem Rest des Tetraminos werden beliebige Farben zugewiesen. Während des gesamten Spiels bleiben alle Farben konstant.
Aufgrund der Form der drei Tetramino ist es unmöglich, aus allen drei Farben in den ersten beiden und letzten beiden Spalten ein Quadrat zu erstellen. Daher beträgt die Mindestbreite des Spielfelds zum Rendern eines Sprites mit einer Breite von 16 Pixeln 2 + 16 + 2 = 20 Quadrate. Es stellte sich jedoch heraus, dass 20 zu wenig ist.
Wie unten gezeigt, kann der Bereich über dem einzelnen unteren Quadrat nicht aus nur einer Linie bestehen, da die einzigen Figuren, die darin passen (Tetramino I), keine Unterstützung haben.
Bei zwei Linien kann das gesamte Spielfeld nur mit Tetramino S und Z gestreckt werden. In diesem Fall bleiben jedoch Löcher in der obersten Linie.
Die Mindestanzahl der Zeilen, die über dem unteren Quadrat erforderlich sind, beträgt 3, und wie oben mehrfach gezeigt, existieren solche Muster. 20 Quadrate sind die Mindestbreite, die erforderlich ist, um ein Sprite mit einer Breite von 16 Pixeln zu platzieren. Aber 20 × 3 + 1 = 61, und diese Zahl ist nicht teilbar durch 4, was bedeutet, dass sie nicht aus Tetramino aufgebaut werden kann. Eine Breite von 21 ergibt jedoch 21 × 3 + 1 = 64, und es kann aus 16 Tetramino gebaut werden. Diese Breite ermöglicht es dem Algorithmus, Sprites mit einer Breite von bis zu 17 Pixeln zu rendern.
Das Spielfeld des ursprünglichen Tetris hat eine Größe von 10 × 20 Quadraten (Verhältnis 1: 2). In dieser Version des Algorithmus bleibt dieses Verhältnis erhalten - das Spielfeld hat eine Größe von 21 × 42 Quadraten.
Da Tetramino J, T und L bei der Erstellung eines Quadrats austauschbar sind und 3 Quadrate dieses Tetramino bei der Erstellung einer Linie darüber beteiligt sind, gibt es 21 - 3 = 18 Muster für die Erstellung eines einzelnen Quadrats. Aufgrund der Spiegelsymmetrie gibt es jedoch nur 9 Zeilen. Für die meisten dieser 9 Zeilen gibt es 3 Zeilen. Eine gründliche Computeruntersuchung ergab jedoch, dass die beiden Muster mehr benötigen. Die nächste mögliche Option sind 7 Zeilen, da 21 × 7 + 1 = 148, was 37 Tetraminos erfordert. Wie in den folgenden Bildern gezeigt, existieren solche Muster.
Mehrere quadratische Muster
Die Muster zum Erstellen mehrerer Quadrate sind auf die gleichen drei Farben beschränkt, die durch die Muster eines einzelnen Quadrats erstellt werden. Die resultierenden Quadrate werden aus Tetramino J, T und L erzeugt, von denen jedes 3 Quadrate in einer Linie oberhalb der Erzeugungslinie belegt. Die maximale Anzahl von Quadraten, die möglicherweise mit einem einzelnen Muster erstellt werden können, beträgt 21/3 = 7. Bei Sprites mit einer Breite von 16 Pixeln kann das Tetramino ganz rechts jedoch kein Quadrat erstellen. Selbst bei Sprites mit einer Breite von 17 Pixeln kann ein Quadrat mit nur einer Farbe erstellt werden. Daher wird das Muster des Erzeugens aus 7 Quadraten selten verwendet.

Die Anzahl der Muster zum Erstellen einer beliebigen Anzahl von Quadraten kann unter Verwendung der Kombinatorik von Aufzählungen bestimmt werden. Betrachten Sie das Muster unten, das eine Reihe über einer Reihe von drei Quadraten darstellt. Jeder Block von drei benachbarten weißen Quadraten bezeichnet einen Teil von Tetramino; erstellte Quadrate werden nicht angezeigt.
Drei Tetramino erzeugen 4 Hohlräume. Es gibt 21 - 3 × 3 = 12 dunkle Quadrate, die beliebig in diese Hohlräume eingefügt werden können, um ein bestimmtes Muster zu bilden. Die Anzahl der Möglichkeiten zur Verteilung dieser dunklen Quadrate kann berechnet werden, indem sie auf eine Linie gesetzt werden, in der einzelne weiße Quadrate als Teiler behandelt werden.
Die Aufgabe war also darauf beschränkt, den Wert des Koeffizienten des Polynoms zu berechnen. Wenn Sie sich diese weißen Quadrate ansehen, können Sie verstehen, dass dies eine Frage der Anzahl der Möglichkeiten ist, 3 von 15 zu wählen.
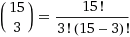
= 455.
Im allgemeinen Fall ist für
n gleich
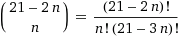
. Aber aufgrund der Spiegelsymmetrie sind sie tatsächlich halb so groß. Wenn die Menge ungerade ist, dann dividieren wir durch zwei und runden auf die nächste ganze Zahl, um ein perfekt symmetrisches Muster darin aufzunehmen, das in dieser Menge existieren sollte, wie zum Beispiel unten für den Fall mit 455 gezeigt.
Wenn wir diese Formel auf 7 Tetramino anwenden, bestätigen wir das Offensichtliche: Es gibt nur ein Muster zum Erstellen von 7 Quadraten.
Das Muster zum Erstellen von 6 Quadraten kann auf zwei Arten erstellt werden: zwei gefüllte Linien (2 × 21 + 6 = 48) und sechs gefüllte Linien (6 × 21 + 6 = 132), für die 12 und 33 Tetramino erforderlich sind. Die obige Formel zeigt, dass es 84 Muster zum Erstellen von 6 Quadraten gibt, von denen jedoch nur 35 aus 2 vollständigen Linien erstellt werden können. 49 Muster erfordern 6 Zeilen. Die Zahlen sind aufgrund der unten gezeigten symmetrischen Muster ungerade.
Es ist auch erwähnenswert, dass hier 2 Linien möglich sind, da im Gegensatz zu dem Muster zum Erzeugen eines Quadrats, das Tetramino S und Z erfordert, 6 Figuren in diesen Mustern verwendet werden.
Die nachstehende Tabelle zeigt die Anzahl der Quadrate, die durch die einzelnen Mustertypen erstellt wurden, die Anzahl der vollständigen Linien, die Anzahl der verwendeten Tetramino und die Anzahl der Muster.
Beispiele für Muster.
Plattformen
Vor dem Erstellen einer Linie untersucht der Algorithmus die Linie darunter. Wenn die untere Reihe nicht alle darüber liegenden Quadrate unterstützen kann, ist eine temporäre Plattform erforderlich. Wenn die Plattform entfernt wird, fällt eine neue Linie ab, und aufgrund der Schwerkraft, die im ursprünglichen Tetris implementiert ist, bleiben einige Quadrate in der Luft hängen.
Die folgende Abbildung zeigt 10 Plattformmuster. Der Bau der Plattform beginnt mit dem Absenken des Tetramino T auf eines der Quadrate der zuletzt erzeugten Linie. Die verbleibenden Tetraminos basieren auf diesem ersten T. Wenn die zuvor erzeugte Linie mindestens 1 Quadrat enthält, wie z. B. das rote Quadrat in der Abbildung unten, können Sie darüber eine flache Plattform erstellen, um die nächste Linie zu erzeugen.
Während des Baus der Plattform wird die unterste Zeile vervollständigt und gelöscht, wobei drei Zeilen darüber verbleiben. Das letzte Tetramino J oder L, das diese Zeilen löscht, wird erst eingefügt, wenn die Erstellungsmuster die nächste Sprite-Zeile oben auf der Plattform erzeugen. Diese letzte Zahl verhindert die Erstellung von Quadraten in der ersten und letzten beiden Zeilen. Wie oben erwähnt, sind die Muster zum Erzeugen von Quadraten aufgrund der Geometrie der Tetramino J, T und L, die in diesem Prozess verwendet werden, auf 17 innere Spalten beschränkt.
Darüber hinaus gibt es oben nur 10 von 19 möglichen Möglichkeiten, Plattformen auf Tetramino T zu bauen.
Gepackte Matrizen
Wie oben erwähnt, werden bei einer Teilmenge der 6 Quadrate nur zwei Zeilen gelöscht. Alle anderen Muster erfordern 6 Zeilen. Um zu verstehen, warum dies der Fall ist, betrachten Sie das folgende Muster.
Diese Tetramino sind austauschbar mit Tetramino J und L, und jedes von ihnen fügt der gemeinsamen Reihe 3 benachbarte Quadrate hinzu. Die auszufüllenden Zeilen werden durch die unten gezeigte Matrix dargestellt.
Jetzt packt das Ganze den leeren Raum mit Tetramino. Links beginnend besteht die einzige Möglichkeit darin, die Tetramino I-Sequenz zu verwenden.
Der verbleibende Platz kann nur mit J und O oder I und L gefüllt werden. Beide Optionen werden unten gezeigt.
Leider werden Tetramino O und L in den oben gezeigten Matrizen nicht unterstützt. Dieses 6-Quadrate-Muster erfordert eine größere Matrix.
Ein ähnliches Problem tritt bei zwei Mustern zum Erzeugen eines Quadrats auf. Betrachten Sie die folgende Matrix:
Die einzige Möglichkeit, die untere Zeile rechts auszufüllen, besteht darin, die Sequenz Z zu verketten.
Ebenso ist der einzige Weg, um 3 leere Felder in der unteren linken Ecke zu bekommen, Tetramino S.
In der mittleren Zeile befindet sich ein leeres Quadrat zwischen S und Z. Sie können es nur mit Tetramino J, T oder L füllen, wie in den folgenden Abbildungen gezeigt.
Durch Einfügen einer dieser Formen wird die Leerstelle geteilt. Der leere Bereich auf der linken Seite enthält 5, 6 bzw. 7 Lücken. Da keiner dieser Werte durch 4 teilbar ist, ist eine Fortsetzung nicht möglich. Für dieses einzelne quadratische Muster ist eine größere Matrix erforderlich.
Dasselbe gilt für ein anderes Muster zum Erstellen eines Quadrats, das in der folgenden Matrix dargestellt ist.
Nachdem Tetramino S und Z verwendet wurden, um den größten Teil der unteren Zeile auszufüllen, befindet sich in der mittleren Zeile ein Leerzeichen zwischen ihnen.
Wie in den folgenden Abbildungen gezeigt, unterteilt der Locheinsatz den leeren Bereich und der leere Bereich auf der linken Seite enthält 9, 10 oder 11 Quadrate. Keine der Zahlen ist durch 4 teilbar.
Packungsmatrizen sind jedoch nicht die einzige Möglichkeit, ein Quadratmuster zu erzeugen. Schauen Sie sich zum Beispiel den 4-Quadrate-Ersteller unten an.
Das Folgende ist ein Versuch, das Muster als Satz von verpackten Tetraminos zu rendern.
Das letzte L wird übersprungen, weil der Platz dafür erst nach der Vervollständigung und Entfernung der dritten Reihe gebildet wird.
Nach einer gründlichen Suche wurde jedoch festgestellt, dass diese Technik die oben genannten Ein-Quadrat-Muster nicht mit der Fähigkeit ausstattet, mit nur 3 Linien zu arbeiten. Außerdem ist es nicht möglich, neue Muster von 6 Quadraten in zwei Zeilen zu implementieren. Die verbleibenden Muster müssen nicht außerhalb der gepackten Matrizen gesucht werden, da sie bereits die geringstmögliche Menge an Tetramino verwenden. Und wenn wir uns auf gepackte Matrizen beschränken, werden wir alle notwendigen Muster viel schneller finden.
Mustersuche
Um die Datenausgabe zu vereinfachen, ist der Tetris-Druckeralgorithmus darauf beschränkt, Tetramino am oberen Mittelpunkt des Spielfelds zu erstellen, es zu drehen, horizontal zu bewegen und abzusenken. Er muss die Figur niemals horizontal bewegen, nachdem er eine Strecke zurückgelegt hat. Diese Einschränkung reduziert den Suchraum erheblich, da es nicht möglich ist, Lücken unter den der Matrix hinzugefügten Zahlen zu bilden. Schauen wir uns als Beispiel die folgende 3-Quadrate-Matrix an.
Wenn wir J in die Mitte der Matrix werfen, wie oben gezeigt, erhalten wir eine Lücke von 2 leeren Quadraten, die nicht mit nachfolgenden Zahlen gefüllt werden können. Daher folgt die Suche diesem Pfad nicht.
Da abgedeckte Lücken nicht zulässig sind, kann jede Spalte in der Matrix als Stapel gefüllter Quadrate betrachtet werden, und die Höhe dieser Stapel beschreibt den Inhalt der gesamten Matrix vollständig. Unabhängig von der Anzahl der Zeilen reicht ein eindimensionales ganzzahliges Array mit 21 Elementen aus, um eine zweidimensionale Matrix zu beschreiben.
Wenn eine Figur in die Matrix fällt, nehmen die Stapelhöhen der entsprechenden Spalten zu. Um diesen Prozess zu beschleunigen, werden alle Tetramine im Voraus analysiert. Es gibt 19 Tetramino-Kurven, und die Suche betrachtet jede von ihnen als eine einzigartige Figur.
Tetramino J in der oberen linken Ecke des Bildes belegt 3 Spalten. Beim Absenken auf die Matrix erhöhen sich die Höhen von 3 benachbarten Stapeln um jeweils 1, 1 und 2 Quadrate. Bevor die Figur abgesenkt werden kann, muss das untere Profil der Figur dem oberen Profil der jeweiligen Stapel entsprechen. Wenn dieses J auf dem Boden des Spielfeldes gelegen hätte, hätte es unter jeder dieser Spalten Lücken von 1, 1 und 0 leeren Feldern geben müssen. Da Abstände verboten sind, müssen die relativen Höhen von 3 Stapeln vollständig mit dem Muster übereinstimmen.
Eine weitere Folge des Fehlens von Lücken war, dass die Zeilen von unten nach oben gefüllt werden, wenn die Figuren in die Matrix fallen. Es ist nicht möglich, eine Zeile in der Mitte einer Matrix zu füllen, bevor oder gleichzeitig nicht alle Zeilen darunter zu vervollständigen. Während des Füllens der Matrix bewegt sich ihre untere Grenze tatsächlich nach oben. Folglich kann ein Matrixspaltenstapel nur dann Unterstützung bieten, wenn seine Höhe abzüglich der Anzahl der vervollständigten Zeilen größer als 0 ist. Wenn der Matrix eine Form hinzugefügt wird, muss mindestens eine der entsprechenden Spalten Unterstützung bieten.
Die Suche speichert ein zweites eindimensionales Array, das die Anzahl der ausgefüllten Quadrate in jeder Zeile enthält. Das obige J enthält in den entsprechenden Zeilen 3 und 1 ein Quadrat. Wenn Sie es in die Matrix einfügen, werden diese Werte zu den entsprechenden Elementen des Arrays hinzugefügt. Die Anzahl der ausgefüllten Zeilen entspricht der Anzahl der Elemente mit dem Wert 21.
Wie im vorherigen Abschnitt angegeben, sollten, wenn die hinzugefügte Figur die Matrix teilt, die Größen der resultierenden Bereiche durch 4 geteilt werden. In der folgenden Abbildung werden durch Hinzufügen von I beispielsweise 2 Bereiche erstellt, von denen jeder 46 leere Quadrate enthält. Da 46 nicht durch 4 teilbar ist, gibt es keine Möglichkeit mehr, den Rest der Matrix auszufüllen.
Die Trennung wird angezeigt, wenn die Höhe des Stapels der Höhe der Matrix entspricht. Nach dem Einfügen der Figur durch Erhöhen der Höhen der jeweiligen Stapel können die Abmessungen aller unterteilten Bereiche des leeren Raums bestimmt werden, indem die Anordnung der Höhen abgetastet wird und der in jedem Stapel verbleibende Raum addiert wird. Diese Nummer wird überprüft und zurückgesetzt, wenn ein Split erkannt wird.
Die zur Erzeugung aller Muster verwendete Suche verwendet eine zufällige inkrementelle Konstruktion, einen Rückverfolgungsalgorithmus, der systematisch alle Kombinationen in zufälliger Reihenfolge überprüft. Die inkrementelle Konstruktion einer Lösung durch zufälliges Einfügen von Formen lässt sie wie einen Kristall wachsen. Zufälligkeit stellt eine Unregelmäßigkeit mit gebrochenen Flächen bereit, die als Grundlage für nachfolgende hinzugefügte Formen dienen. Der größte Teil der Matrix wird sehr schnell zufällig gepackt, und wenn der leere Raum knapp wird, kommt das Backtracking ins Spiel.
Vor dem Durchführen der Suche werden zufällige Permutationen von 371 Möglichkeiten zum Hinzufügen einer Figur zur Matrix durchgeführt. Der Pseudocode der Suchfunktion wird unten angezeigt.
private Result search(Matrix matrix, int remaining) { if (remaining == 0) { return SOLUTION } attempts := attempts + 1 if (attempts >= MAX_ATTEMPTS) { return TIMEOUT } if ( S Z) { S Z if ( ) { Result result := search(matrix, remaining - 1) if (result == SOLUTION) { return SOLUTION } if (result == TIMEOUT) { return TIMEOUT } } } for( , ) { if ( ) { Result result := search(matrix, remaining - 1) if (result == SOLUTION) { return SOLUTION } if (result == TIMEOUT) { return TIMEOUT } } } return NO_SOLUTION }
Die ursprüngliche Matrix, die an die Suchfunktion übergeben wurde, ist leer, mit Ausnahme der untersten Reihe mit Blöcken aus 3 benachbarten Quadraten. Es wird zusammen mit der Anzahl der verbleibenden Zahlen übertragen, die hinzugefügt werden müssen. Wenn der
remaining Wert 0 ist, enthält die Matrix die Lösung und die Funktion kehrt zurück. Jeder rekursive Aufruf erhöht die globale Anzahl der
attempts . Wenn der Wert
MAX_ATTEMPTS mit dem Wert 1000 überschritten
MAX_ATTEMPTS , wird die Suche erneut
MAX_ATTEMPTS .
Die dritte
if versucht, Tetramino S oder Z am unteren Rand der Matrix einzufügen, wenn der Platz dies zulässt. Dies bedeutet, Situationen wie die unten gezeigte zu vermeiden, in denen der Algorithmus Zeit damit verbringt, einen Teil der Matrix zu füllen, und den Rest aufgrund mangelnder Unterstützung nicht füllen kann.
Dank der
if schnell eine Plattform, auf der aufgebaut werden kann:
Um zu versuchen, der Matrix eine Zahl hinzuzufügen, sind die obigen Prüfungen erforderlich. Der Algorithmus prüft anhand der ausgefüllten Zeilen, ob die Figur unterstützt wird. Außerdem wird geprüft, ob die Größe jedes einzelnen leeren Bereichs, der durch das Einfügen der Form erstellt wird, durch 4 geteilt wird.
Bildkonvertierung
Tetris Printer Algorithm konvertiert jede Zeile der Bitmap in eine Reihe von Durchläufen. Von links nach rechts bewegt, fügt jede Passage auf "gierige" Weise Tetramino J, T und L dort ein, wo sie platziert sind. Das folgende Bild zeigt beispielsweise eine Zeile mit 16 Pixeln einer Bitmap.
Das Bild unten zeigt die 5 Durchgänge, die erforderlich sind, um diese 16 Pixel abzudecken.
Die Folge von Formen, die der Algorithmus einzufügen versucht, wird durch die Farben der Pixel bestimmt. Damit sich die Formen nicht überlappen, wird ein eindimensionales Array von Booleschen Werten verwendet. Um eine Zahl einzufügen, müssen 3 Nullelemente im Array vorhanden sein. Nach dem erfolgreichen Einfügen von Abbildung 3 nehmen die entsprechenden Array-Elemente den Wert 1 an.
Um vervollständigte Pixel zwischen mehreren Durchläufen zu verfolgen, wird ein zweites eindimensionales Array von Booleschen Werten verwendet. Wenn jedes Element 1 ist, ist die Zeile abgeschlossen.
Am Ende jedes Durchgangs durchsucht der Bildkonverter die Tabelle nach allen Mustern, um ein oder mehrere Quadrate zu erstellen. Für die Ausgabe wird das entsprechende Muster mit den unten eingefügten Tetramino J, T und L übergeben. Der oben gezeigte erste Durchgang wird beispielsweise als das folgende Muster zum Erstellen von 5 Quadraten angezeigt:
Echtzeitsuche
Der im vorherigen Abschnitt beschriebene Bildkonverter ist extrem schnell, da er eine konstante Tabelle verwendet, die alle Muster zum Erstellen von Quadraten enthält, und diese nicht in Echtzeit durchsucht. Bei der Echtzeitsuche können jedoch Muster verwendet werden, die nicht in der Tabelle enthalten sind, und daher wird die Menge an Tetramino, die zum Generieren des Bildes benötigt wird, erheblich reduziert. Er verwendet die in früheren Passagen erstellten Quadrate als zusätzliche Stützen. Wie oben erwähnt, sind für das folgende Muster zum Erstellen eines Quadrats 7 vollständige Linien erforderlich.
Ein rotes Quadrat, das im vorherigen Abschnitt in der unteren linken Ecke des Bilds unten erstellt wurde, bietet jedoch zusätzliche Unterstützung und reduziert die Anzahl der gefüllten Linien auf 3.
Zusätzlich kann eine Echtzeitsuche 3 benachbarte Pixel derselben Farbe durch Umdrehen von Tetramino J, T oder L erfassen.
Tatsächlich kann es invertiertes und invertiertes Tetramino kombinieren und eine große Anzahl von Pixeln in einem Durchgang abdecken. Beispielsweise können die obigen 5 Durchgänge, die zum Abdecken von 16 Pixeln erforderlich sind, auf den unten gezeigten einzelnen Durchgang reduziert werden.
Um dieses Muster zu erhalten, beginnt der Bildkonverter mit dem eifrigen Packen der umgedrehten Tetramino J, T und L.
Dann versucht er eifrig, die nicht umgedrehten Versionen hinzuzufügen, und in diesem Fall schafft er es, ein weiteres J hinzuzufügen.
Grundsätzlich kann in diesem Prozess auch eine vorberechnete Nachschlagetabelle verwendet werden, die jedoch aufgrund ihrer Größe in der Praxis nicht anwendbar ist.
In diesem Beispiel werden 8 Quadrate in einer Reihe über der zu erstellenden Reihe zur unteren Reihe der leeren Matrix hinzugefügt. Für
n Felder auf einem 21 Felder breiten Spielfeld ist die Höhe der Matrix
h die kleinste positive ganze Zahl, so dass
21h - n durch 4 teilbar ist. In diesem Fall ist eine Matrix der Höhe 4 erforderlich.
Die Echtzeitsuche funktioniert genauso wie der oben beschriebene Suchalgorithmus, weist jedoch geringfügige Verbesserungen auf. Wie zuvor bietet der Matrixspaltenstapel nur dann Unterstützung, wenn die Spaltenhöhe abzüglich der Anzahl der vervollständigten Zeilen größer als Null ist. Wenn die Differenz Null ist, sollte der Spaltenstapel keine Unterstützung bieten. Wenn es in dieser Version jedoch gleich Null ist, werden die Quadrate in der erstellten Linie überprüft, die durch vorherige Durchgänge generiert wurden. Das heißt, alle Quadrate in der Zeile unter der unteren Zeile der Matrix unterstützen leere Spalten.
Da die Suche in Echtzeit durchgeführt wird, ist es außerdem unpraktisch, sie vollständig zu gestalten. Wenn er nach einer bestimmten Anzahl von Versuchen keine Lösung gefunden hat, fügt er 4 weitere Zeilen oben in die Matrix ein und versucht es dann erneut. Wenn er nach einer bestimmten Anzahl von Versuchen immer noch keine Lösung finden konnte, kehrt er in der aktuellen Passage zu der im vorherigen Abschnitt des Artikels beschriebenen Methode mit vorberechneten Suchtabellen und Bildkonvertierung zurück.
Drucken
Zum Drucken müssen Sie die Anweisungen befolgen, die vom Bildkonverter auf dem Tetris-Spielfeld angezeigt werden. Der Drucker erstellt ein bestimmtes Tetramino am oberen Mittelpunkt des Spielfelds in einer Standardausrichtung. Dann dreht der Drucker ihn, bewegt ihn horizontal und senkt ihn ab. Dieser Vorgang wird im Video gezeigt:
Quellcode
Der Quellcode für das Java 7-Projekt ist
hier verfügbar.
Suchalgorithmen für vorbereitete Tabellen und in Echtzeit befinden sich in den Paketen
search.precomputed und
search.realtime . Sie verwenden einige gängige Klassen im Suchpaket. Die Ergebnisse einer vorberechneten Suche werden als Folge von Textdateien im Musterpaket gespeichert. Textdateien speichern gepackte Matrizen als ASCII-Zeichen, beginnend mit
A Zum Beispiel sehen die ersten 3 Matrizen in
emitters1.txt (der Satz von Mustern zum Erstellen eines Quadrats) folgendermaßen aus:
Wie im Artikel wiederholt angegeben, können 3 benachbarte
A Symbole in den obigen Matrizen durch Tetramino J, T oder L ersetzt werden. Die Symbole
B ,
C ,
D usw. repräsentieren die Sequenz von Tetramino, die Sie erstellen müssen.
Die
imageconverter.ImageConverter Klasse enthält die
main Methode, die ein einziges Befehlszeilenargument empfängt: den Namen der Image-Sprite-Datei. Ein Bild kann nicht größer als 17 × 32 Pixel sein und nicht mehr als 3 undurchsichtige Farben enthalten. Alle anderen Pixel müssen transparent sein.
Interessanterweise verwendeten Entwickler in alten Videospielen häufig den Hintergrund, um zusätzliche Farben zu erhalten. Zum Beispiel Pupillen und Mund von Bubble von Bubble bobble, Pupillen von Donkey Kong von Donkey Kong und Augenbrauen mit Miss Pakmans Maulwurf von Frau Pac-Man ist eigentlich transparent. Schwarz wird von einem festen Hintergrund erhalten.
Der Hintergrund des Tetris-Spielfelds kann auf ähnliche Weise verwendet werden.
ImageConverter Ausgabe von
ImageConverter sieht folgendermaßen aus:
Die 3 Hex-Werte in der ersten Zeile sind 3 undurchsichtige Farben, die aus der Sprite-Bilddatei extrahiert wurden. Sie entsprechen den Farben von Tetramino J, T und L. Die Farben anderer Tetramino beeinflussen das Bild nicht. Die verbleibenden Blöcke sind Musterpakete, die auf dem Spielfeld ausgeführt werden (für Zeichen nach
Z und bis zu
a siehe die
Tabelle der ASCII-Zeichen ). Die hervorgehobenen gelben Blöcke bilden die Plattform. Der erste Block fügt die Plattform hinzu, der zweite entfernt sie.
Die
printer.Printer Klasse empfängt eine Textdatei in diesem Format und generiert eine Bilddatei, indem sie Tetris spielt.
Der Druckeralgorithmus, der zum Erzeugen eines Videos verwendet wird, das der
NES-Version von Tetris ähnelt, definiert jeden Tetramino-Typ in jedem Block einer Textdatei. Dann bewegt es sich in umgekehrter Reihenfolge vom Startpunkt und der ursprünglichen Ausrichtung zum Drehwinkel und den Koordinaten des Absenkens der in der Datei angegebenen Figur. Hinweis: Aufgrund der extrem hohen Geschwindigkeit fallender Figuren ist es in der echten NES-Version von Tetris unmöglich, Level 30 zu überschreiten. Es wird davon ausgegangen, dass der Drucker alle seine Befehle schnell genug auf das Spielfeld überträgt. um dies zu kompensieren.
Verwenden Sie
search.precomputed.PatternSearcher , um
search.precomputed.PatternSearcher . Es kann angepasst werden, indem die Konstanten am Anfang der Quellcodedatei geändert werden.
public static final int MATRIX_WIDTH = 21; public static final int MATRIX_HEIGHT = 4; public static final int EMITTED_SQUARES = 4; public static final int RANDOM_SETS = 100000; public static final int MAX_ATTEMPTS = 1000;
RANDOM_SETS ist die Anzahl der zufälligen Permutationen von 371 Möglichkeiten, der Matrix eine Zahl hinzuzufügen. Bei Einstellung auf
100000 dauert es einige Sekunden, um die Permutationen beim Start zu initialisieren. Darüber hinaus benötigt ihr Speicher mehr als ein Gigabyte Speicher.
MAX_ATTEMPTS steuert die Ausführungszeit der Suche. Ein relativ kleiner Wert von
1000 ermöglicht es der Suche, zufällige Anfänge, die sich nicht gut zeigen, schnell zu verwerfen. Um jedoch zu beweisen, dass es für eine bestimmte Matrixgröße und die Anzahl der erstellten Quadrate keine Lösung gibt, muss der gesamte Suchraum vollständig untersucht werden. Dazu können Sie
MAX_ATTEMPTS auf
Integer.MAX_VALUE .
Ähnliche Konstanten finden Sie in
search.realtime.RealtimeSearcher , das vom Bildkonverter verwendet wird. Wie oben erwähnt, erfordert ein großer
RANDOM_SETS Wert eine Erhöhung des maximalen Speichers und führt zu einem längeren Start.
MAX_RETRIES steuert die Anzahl der Versuche, nach denen die Echtzeitsuche
MAX_RETRIES wird und mit einer vorberechneten Tabelle zur Suche zurückkehrt.
Beachten Sie, dass beide Suchalgorithmen 100% der CPU belegen und viele parallele Threads erstellen, deren Größe der Anzahl der verfügbaren Prozessoren entspricht.