Vorhersagen versus Erklärungen: oder warum mehr „Semi-Buys“ im Bereich Data Science benötigt werden

Phoebe Wong, Wissenschaftlerin und CFO bei Equal Citizens, sprach über den kulturellen Konflikt in der Kognitionswissenschaft. Elena Kuzmina übersetzte den Artikel ins Russische.

Vor einigen Jahren habe ich eine Diskussion über die Verarbeitung natürlicher Sprache gesehen. Es sprachen der „Vater der modernen Linguistik“ Noam Chomsky und der neue Wachsprecher Peter Norvig , Forschungsdirektor bei Google. Chomsky überlegte, in welche Richtung sich die Sphäre der Verarbeitung natürlicher Sprache bewegt, und sagte :

Angenommen, jemand ist im Begriff, eine Physikabteilung aufzulösen, und möchte dies nach den Regeln tun. Nach den Regeln bedeutet dies, eine unendliche Anzahl von Videos über das Geschehen auf der Welt aufzunehmen, diese Gigabyte an Daten an den größten und schnellsten Computer weiterzuleiten und eine komplexe statistische Analyse durchzuführen Was passiert vor deinem Fenster? Tatsächlich erhalten Sie eine bessere Prognose als die der Fakultät für Physik. Wenn der Erfolg davon abhängt, wie nah Sie an der Masse chaotischer Rohdaten sind, ist dies besser als die Vorgehensweise der Physiker: keine Gedankenexperimente auf idealen Oberflächen und so weiter. Aber Sie werden nicht die Art von Verständnis bekommen, nach der die Wissenschaft immer gesucht hat. Was Sie bekommen, ist nur eine ungefähre Vorstellung davon, was in der Realität passiert.

* Von der Bayes-Wahrscheinlichkeit - eine Interpretation des Wahrscheinlichkeitsbegriffs, bei der Wahrscheinlichkeit anstelle der Häufigkeit oder Tendenz zu einem bestimmten Phänomen als vernünftige Erwartung interpretiert wird, die eine quantitative Einschätzung eines persönlichen Glaubens oder Wissensstandes darstellt. Forscher der künstlichen Intelligenz verwenden Bayes'sche Statistiken beim maschinellen Lernen, um Computern zu helfen, Muster zu erkennen und darauf basierende Entscheidungen zu treffen.

Chomsky betonte wiederholt diese Idee: Der heutige Erfolg bei der Verarbeitung der natürlichen Sprache, nämlich die Genauigkeit der Vorhersage, ist keine Wissenschaft. Ihm zufolge ist das Werfen eines riesigen Textstücks in eine „komplexe Maschine“ lediglich eine Annäherung an die Rohdaten oder das Sammeln von Insekten, was nicht zu einem wirklichen Verständnis der Sprache führen wird.

Laut Chomsky besteht das Hauptziel der Wissenschaft darin, erklärende Prinzipien für die tatsächliche Funktionsweise des Systems zu entdecken. Der richtige Ansatz, um dieses Ziel zu erreichen, besteht darin, der Theorie die Möglichkeit zu geben, Daten zu leiten. Es ist notwendig, die grundlegende Natur des Systems zu untersuchen, indem man mit Hilfe sorgfältig entworfener Experimente von "irrelevanten Einschlüssen" abstrahiert, das heißt auf die gleiche Weise, wie es in der Wissenschaft seit Galileo akzeptiert wurde.

In seinen Worten:

Es ist unwahrscheinlich, dass ein einfacher Versuch, mit chaotischen Rohdaten umzugehen, irgendwohin führt, so wie Galileo nicht irgendwohin.

Anschließend antwortete Norwig in einem langen Aufsatz auf Chomskys Behauptungen. Norvig merkt an, dass in fast allen Bereichen der Anwendung der Sprachverarbeitung: Suchmaschinen, Spracherkennung, maschinelle Übersetzung und Beantwortung von Fragen geschulte Wahrscheinlichkeitsmodelle Vorrang haben, da sie viel besser funktionieren als alte Werkzeuge, die auf theoretischen oder logischen Regeln basieren. Er sagt, dass Chomskys Erfolgskriterium in der Wissenschaft - die Betonung der Frage nach dem Warum und die Untertreibung der Bedeutung des Wie - falsch ist.

Bestätigt er seine Position, zitiert er Richard Feynman: "Physik kann sich ohne Beweise entwickeln, aber wir können uns nicht ohne Fakten entwickeln." Norwig erinnert sich, dass probabilistische Modelle mehrere Billionen Dollar pro Jahr generieren, während Nachkommen von Chomskys Theorie unter Berufung auf Chomskys bei Amazon verkaufte Bücher weit weniger als eine Milliarde verdienen.

Norwig schlägt vor, dass Chomskys Verachtung für das „Bayes'sche Hin und Her“ auf die Trennung der beiden Kulturen in der von Leo Breiman beschriebenen statistischen Modellierung zurückzuführen ist :

1. Eine Datenmodellierungskultur , die davon ausgeht, dass die Natur eine Black Box ist, in der Variablen stochastisch miteinander verbunden sind. Die Arbeit von Modellierungsexperten besteht darin, das Modell zu bestimmen, das am besten zu den zugrunde liegenden Assoziationen passt.
2. Die Kultur der algorithmischen Modellierung impliziert, dass Assoziationen in einer Black Box zu komplex sind, um mit einem einfachen Modell beschrieben zu werden. Die Arbeit der Modellentwickler besteht darin, den Algorithmus auszuwählen, der das Ergebnis am besten anhand von Eingabevariablen bewertet, ohne zu erwarten, dass die wahren grundlegenden Zuordnungen von Variablen in der Black Box verstanden werden können.

Norwig meint, dass Chomsky nicht so sehr mit probabilistischen Modellen als solchen polemisiert, sondern algorithmische Modelle mit „Billiarden-Parametern“ nicht akzeptiert: Sie sind nicht einfach zu interpretieren und daher für die Lösung der Fragen nach dem „Warum“ unbrauchbar.
Norwig und Breiman gehören zu einem anderen Lager - sie glauben, dass Systeme wie Sprachen zu komplex, zufällig und willkürlich sind, um durch einen kleinen Satz von Parametern dargestellt zu werden. Wenn man von Schwierigkeiten abstrahiert, ist dies mit einem mystischen Werkzeug vergleichbar, das auf einen bestimmten permanenten Bereich abgestimmt ist, der nicht wirklich existiert. Daher wird die Frage, was Sprache ist und wie sie funktioniert, übersehen.

Norwig bekräftigt seine These in einem anderen Artikel , in dem er argumentiert, dass wir aufhören sollten, so zu handeln, wie es unser Ziel ist, äußerst elegante Theorien zu schaffen. Stattdessen müssen Sie Komplexität akzeptieren und unseren besten Verbündeten einsetzen - unangemessene Dateneffizienz. Er weist darauf hin, dass bei der Spracherkennung, der maschinellen Übersetzung und fast allen maschinellen Lernanwendungen für Webdaten einfache Modelle wie n-Gramm-Modelle oder lineare Klassifikatoren, die auf Millionen spezifischer Funktionen basieren, besser funktionieren als komplexe Modelle. die versuchen, die allgemeinen Regeln zu entdecken.

Was mich an dieser Diskussion am meisten reizt, ist nicht, womit Chomsky und Norvig nicht einverstanden sind, sondern worin sie vereint sind. Sie sind sich einig, dass die Analyse großer Datenmengen mit statistischen Lernmethoden ohne Verständnis von Variablen bessere Vorhersagen liefert als ein theoretischer Ansatz, der versucht, die Beziehung zwischen Variablen zu modellieren.

Und ich bin nicht der einzige, der sich darüber wundert: Viele Menschen mit mathematischem Hintergrund, mit denen ich gesprochen habe, finden dies auch widersprüchlich. Sollte der Ansatz, der sich am besten zur Modellierung grundlegender struktureller Beziehungen eignet, nicht auch die größte Vorhersagekraft haben? Oder wie können wir etwas genau vorhersagen, ohne zu wissen, wie alles funktioniert?

Vorhersagen gegen die Verursachung

Selbst in akademischen Bereichen wie Wirtschafts- und anderen Sozialwissenschaften werden die Konzepte der Vorhersage- und Erklärungskraft oft miteinander kombiniert.

Modelle, die eine hohe Erklärungsfähigkeit aufweisen, gelten häufig als sehr aussagekräftig. Der Ansatz zur Erstellung des besten Vorhersagemodells unterscheidet sich jedoch grundlegend vom Ansatz zur Erstellung des besten Erklärungsmodells, und Modellierungsentscheidungen führen häufig zu Kompromissen zwischen den beiden Zielen. Die methodischen Unterschiede sind in Einführung in das statistische Lernen (ISL) dargestellt.

Vorhersagemodellierung

Das Grundprinzip von Vorhersagemodellen ist relativ einfach: Bewerten Sie Y anhand eines Satzes leicht verfügbarer Eingabedaten X. Wenn der Fehler X im Durchschnitt Null ist, kann Y vorausgesagt werden mithilfe von:

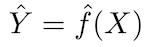
wobei ƒ die systematische Information über Y ist, die von X geliefert wird und zu Ŷ (Vorhersage von Y) für ein gegebenes X führt. Die genaue Funktionsform ist normalerweise nicht signifikant, wenn sie Y vorhersagt, und ƒ wird als „Black Box“ betrachtet.

Die Genauigkeit dieses Modelltyps kann in zwei Teile zerlegt werden: einen reduzierbaren Fehler und einen schwerwiegenden Fehler:

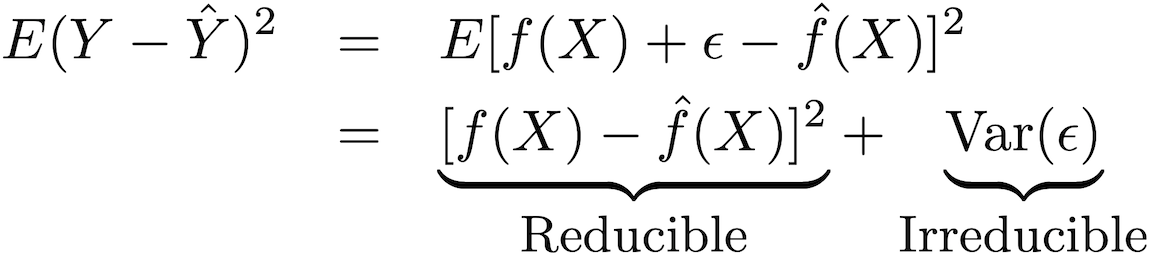
Um die Genauigkeit der Vorhersage des Modells zu erhöhen, ist es erforderlich, den reduzierbaren Fehler zu minimieren und die am besten geeigneten Methoden des statistischen Trainings für die Schätzung zu verwenden, um ƒ zu bewerten.

Ausgabemodellierung

ƒ kann nicht als „Black Box“ betrachtet werden, wenn das Ziel darin besteht, die Beziehung zwischen X und Y zu verstehen (wie sich Y als Funktion von X ändert). Weil wir die Auswirkung von X auf Y nicht bestimmen können, ohne die funktionale Form zu kennen ƒ.

Fast immer werden bei der Modellierung von Schlussfolgerungen parametrische Methoden verwendet, um ƒ zu schätzen. Das parametrische Kriterium bezieht sich darauf, wie dieser Ansatz die Schätzung von ƒ vereinfacht, indem er die parametrische Form ƒ annimmt und ƒ anhand der vorgeschlagenen Parameter bewertet. Dieser Ansatz besteht aus zwei Hauptschritten:

1. Machen Sie eine Annahme über die Funktionsform ƒ. Die häufigste Annahme ist, dass ƒ in X linear ist:



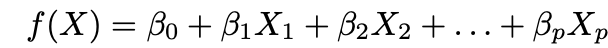
2. Passen Sie die Daten an das Modell an, dh finden Sie die Werte der Parameter β₀, β₁, ..., βp so, dass:


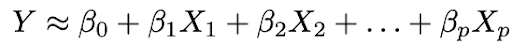
Der gebräuchlichste Modellanpassungsansatz ist die Methode der kleinsten Quadrate (OLS).

Der Kompromiss zwischen Flexibilität und Interpretierbarkeit

Sie fragen sich vielleicht schon: Woher wissen wir, dass ƒ linear ist? Tatsächlich werden wir es nicht wissen, da die wahre Form ƒ unbekannt ist. Und wenn das ausgewählte Modell zu weit vom tatsächlichen Modell entfernt ist, werden unsere Schätzungen verzerrt. Warum wollen wir also überhaupt eine solche Annahme machen? Weil es einen inhärenten Kompromiss zwischen Modellflexibilität und Interpretierbarkeit gibt.

Flexibilität bezieht sich auf die Formenpalette, die ein Modell erstellen kann, um den vielen verschiedenen möglichen funktionalen Formen zu entsprechen. Je flexibler das Modell ist, desto besser kann es angepasst werden, was die Genauigkeit der Prognose erhöht. Ein flexibleres Modell ist jedoch komplexer und erfordert eine Anpassung von mehr Parametern, und -Schätzungen werden häufig zu komplex, als dass die Assoziationen einzelner Prädiktoren und Prognosefaktoren interpretiert werden könnten.

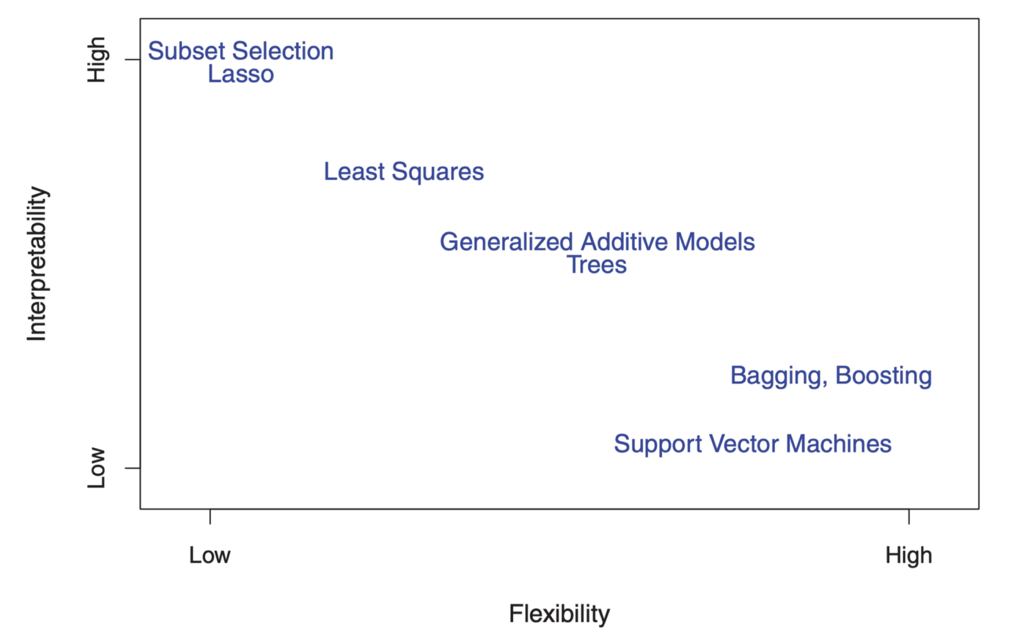
Auf der anderen Seite sind die Parameter im linearen Modell relativ einfach und interpretierbar, auch wenn es keine sehr gute Prognose liefert. Hier ist ein großartiges Diagramm in ISL, das diesen Kompromiss in verschiedenen statistischen Trainingsmodellen veranschaulicht:
" "

Wie Sie sehen, sind flexiblere Modelle für maschinelles Lernen mit besserer Prognosegenauigkeit, wie die Support-Vektor-Methode und die Verbesserungsmethoden, gleichzeitig schlecht interpretierbar. Inferenzmodellierung verweigert auch die Prognosegenauigkeit des interpretierten Modells, wodurch eine sichere Annahme über die funktionale Form f getroffen wird.

Ursachenermittlung und kontrafaktische Begründung

Aber warte einen Moment! Selbst wenn Sie ein gut interpretiertes Modell mit guter Übereinstimmung verwenden, können Sie diese Statistiken nicht als separaten Beweis für die Kausalität verwenden. Dies liegt an dem alten, müden Klischee "Korrelation ist keine Kausalität".

Hier ist ein gutes Beispiel : Angenommen, Sie haben Daten über die Länge von hundert Fahnenmasten, die Länge ihrer Schatten und den Sonnenstand. Sie wissen, dass die Länge des Schattens von der Länge des Pols und dem Stand der Sonne abhängt. Auch wenn Sie die Länge des Pols als abhängige Variable und die Länge des Schattens als unabhängige Variable festlegen, passt Ihr Modell dennoch zu statistisch signifikanten Koeffizienten und so weiter.

Deshalb können Kausalzusammenhänge nicht nur durch statistische Modelle hergestellt werden und erfordern Grundkenntnisse - die angebliche Kausalität sollte durch ein vorläufiges theoretisches Verständnis des Zusammenhangs gerechtfertigt sein. Daher basieren Datenanalyse und statistische Modellierung von Ursache-Wirkungs-Beziehungen häufig weitgehend auf theoretischen Modellen.

Und selbst wenn Sie eine gute theoretische Begründung dafür haben, dass X Y verursacht, ist die Identifizierung eines Kausaleffekts oftmals sehr schwierig. Dies liegt daran, dass bei der Bewertung eines Kausalzusammenhangs ermittelt werden muss, was in einer gegenaktiven Welt passieren würde, in der X nicht stattgefunden hat, was per Definition nicht beobachtbar ist.

Hier ist ein weiteres gutes Beispiel : Angenommen, Sie möchten die gesundheitlichen Auswirkungen von Vitamin C bestimmen. Haben Sie Daten darüber, ob jemand Vitamine einnimmt (X = 1, wenn er einnimmt; 0 - nicht einnimmt), und einige binäre Gesundheitsergebnisse (Y = 1, wenn er gesund ist; 0 - nicht gesund), dass sieht so aus:

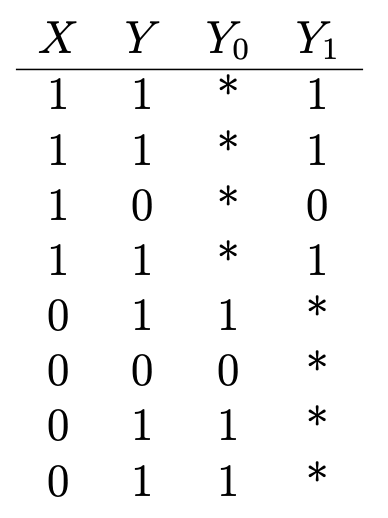
Y₁ ist das gesundheitliche Ergebnis derjenigen, die Vitamin C einnehmen, und Y₀ ist das gesundheitliche Ergebnis derjenigen, die es nicht sind. Um die Wirkung von Vitamin C auf die Gesundheit zu bestimmen, bewerten wir die durchschnittliche Wirkung der Behandlung:

$$$= E (Y & sub1;) - E (Y & sub4;)$

Dazu ist es jedoch wichtig zu wissen, welche gesundheitlichen Konsequenzen die Einnahme von Vitamin C haben würde, wenn sie kein Vitamin C einnehmen und umgekehrt (oder E (Y₀ | X = 1) und E (Y₁ |) X = 0)), die in der Tabelle durch Sternchen gekennzeichnet sind und unbeobachtete kontrafaktische Ergebnisse darstellen. Der durchschnittliche Behandlungseffekt kann ohne diese Eingabe nicht sequenziell bewertet werden.

Stellen Sie sich nun vor, dass bereits gesunde Menschen in der Regel versuchen, Vitamin C einzunehmen, aber bereits ungesunde Menschen dies nicht tun. In diesem Szenario würden Beurteilungen einen starken Heileffekt zeigen, selbst wenn Vitamin C die Gesundheit überhaupt nicht beeinträchtigen würde. Der bisherige Gesundheitszustand wird als Mischfaktor bezeichnet, der sowohl die Vitamin C-Aufnahme als auch die Gesundheit (X und Y) beeinflusst und zu verzerrten Schätzungen führt. Der sicherste Weg, einen konsistenten θ-Score zu erhalten, besteht darin, die Behandlung durch Experimente zu randomisieren, sodass X nicht von Y abhängig ist.

Wenn die Behandlung nach dem Zufallsprinzip verordnet wird, wird das Ergebnis der Gruppe, die das Arzneimittel im Durchschnitt nicht erhält, zu einem objektiven Indikator für die kontrafaktischen Ergebnisse der Gruppe, die die Behandlung erhält, und stellt sicher, dass kein Verzerrungsfaktor vorliegt. A / B-Tests orientieren sich an diesem Verständnis.

Aber randomisierte Experimente sind nicht immer möglich (oder ethisch, wenn wir die gesundheitlichen Auswirkungen des Rauchens oder Essens von zu vielen Schokoladenkeksen untersuchen möchten), und in diesen Fällen sollten die ursächlichen Auswirkungen aus Beobachtungen mit häufig nicht randomisierten Behandlungen abgeschätzt werden.

Es gibt viele statistische Methoden , mit denen kausale Effekte unter nicht experimentellen Bedingungen identifiziert werden können. Sie tun dies, indem sie kontrafaktische Ergebnisse konstruieren oder zufällige Behandlungsvorschriften in Beobachtungsdaten modellieren.

Es ist leicht vorstellbar, dass die Ergebnisse dieser Analysetypen oft nicht sehr zuverlässig oder reproduzierbar sind. Und noch wichtiger: Diese Ebenen methodischer Hindernisse sollen nicht die Genauigkeit der Vorhersage des Modells verbessern, sondern den Nachweis der Kausalität durch eine Kombination aus logischen und statistischen Schlussfolgerungen erbringen.

Es ist viel einfacher, den Erfolg einer Prognose zu messen als ein Kausalmodell. Obwohl es Standard-Leistungsindikatoren für Prognosemodelle gibt, ist es viel schwieriger, den relativen Erfolg von Kausalmodellen zu bewerten. Wenn es jedoch schwierig ist, Ursache und Wirkung aufzuspüren, heißt das nicht, dass wir aufhören sollten, es zu versuchen.
Der Hauptpunkt hierbei ist, dass prognostische und kausale Modelle völlig unterschiedlichen Zwecken dienen und völlig unterschiedliche Daten und statistische Modellierungsprozesse erfordern, und oft müssen wir beides tun.

Ein Beispiel aus der Filmindustrie zeigt: Studios verwenden Prognosemodelle, um Einnahmen an den Kinokassen zu prognostizieren, die finanziellen Ergebnisse des Filmvertriebs vorherzusagen, die finanziellen Risiken und die Rentabilität ihres Filmportfolios zu bewerten usw. Prognosemodelle werden uns jedoch nicht näher an die Struktur und Dynamik des Filmmarkts heranführen und helfen nicht dabei Investitionsentscheidungen, weil in den früheren Phasen des Filmproduktionsprozesses (in der Regel Jahre vor dem Erscheinungsdatum), wenn Investitionsentscheidungen getroffen werden, die Varianz möglich ist Die Ergebnisse sind hoch.

Daher ist die Genauigkeit von Vorhersagemodellen, die auf Anfangsdaten in den frühen Stadien basieren, stark verringert. Vorhersagemodelle nähern sich dem Startdatum des Filmvertriebs, wenn die meisten Produktionsentscheidungen bereits getroffen wurden und die Prognose nicht mehr besonders realisierbar und relevant ist. Andererseits können die Studios durch die Modellierung von Ursache-Wirkungs-Beziehungen herausfinden, wie verschiedene Produktionsmerkmale das potenzielle Einkommen in den frühen Phasen der Filmproduktion beeinflussen können und sind daher für die Information über ihre Produktionsstrategien von entscheidender Bedeutung.

Erhöhte Aufmerksamkeit für Vorhersagen: Hatte Chomsky recht?

Es ist leicht zu verstehen, warum Chomsky verärgert ist: Prognosemodelle dominieren die wissenschaftliche Gemeinschaft und die Industrie. Eine Textanalyse akademischer Preprints zeigt, dass die am schnellsten wachsenden Bereiche der quantitativen Forschung den Prognosen immer mehr Aufmerksamkeit schenken. Beispielsweise hat sich die Anzahl der Artikel auf dem Gebiet der künstlichen Intelligenz, in denen „Vorhersage“ erwähnt wird, mehr als verdoppelt, während sich die Anzahl der Artikel zu Schlussfolgerungen seit 2013 halbiert hat.

In datenwissenschaftlichen Lehrplänen werden Ursache-Wirkungs-Beziehungen weitgehend ignoriert. Die Datenwissenschaft in der Wirtschaft konzentriert sich hauptsächlich auf Vorhersagemodelle. Renommierte Feldwettbewerbe wie der Kaggle- und der Netflix-Preis basieren auf der Verbesserung der prädiktiven Leistungsindikatoren.

Andererseits gibt es noch viele Bereiche, in denen der empirischen Vorhersage nicht genügend Aufmerksamkeit geschenkt wird, und sie können von den im Bereich des maschinellen Lernens und der prädiktiven Modellierung erzielten Errungenschaften profitieren. Die Darstellung des aktuellen Zustands als Kulturkrieg zwischen dem „Chomsky-Team“ und dem „Norvig-Team“ ist jedoch falsch: Es gibt keinen Grund, warum nur eine Option gewählt werden muss, denn es gibt viele Möglichkeiten zur gegenseitigen Bereicherung zwischen den beiden Kulturen. Es wurde viel Arbeit geleistet, um Modelle für maschinelles Lernen verständlicher zu machen. Susan Ati aus Stanford verwendet beispielsweise Methoden des maschinellen Lernens in einer Kausalzusammenhangsmethodik.

Um positiv abzuschließen, erinnern Sie sich an die Arbeiten von Jude Pearl . Pearl leitete in den 1980er Jahren ein Forschungsprojekt zur künstlichen Intelligenz, das es Maschinen ermöglichte, probabilistisch mit Bayes'schen Netzwerken zu argumentieren. Seitdem ist er jedoch der größte Kritiker geworden, wie die Aufmerksamkeit der künstlichen Intelligenz ausschließlich auf probabilistische Assoziationen und Korrelationen zu einem Hindernis für Erfolge wurde.

Pearl teilt die Meinung von Chomsky und argumentiert, dass all die beeindruckenden Leistungen des Deep Learning darauf hinauslaufen, die Kurve an die Daten anzupassen. Heutzutage steckt die künstliche Intelligenz fest und tut dieselben Dinge (zum Vorhersagen und Diagnostizieren und Klassifizieren) wie Maschinen vor 30 Jahren. Jetzt sind Autos nur unwesentlich besser, während Vorhersage und Diagnose „nur die Spitze der menschlichen Intelligenz“ sind.

Er glaubt, dass der Schlüssel zur Schaffung wirklich intelligenter Maschinen, die wie Menschen denken, darin liegt, Maschinen das Nachdenken über Ursache und Wirkung beizubringen, damit diese Maschinen widersprüchliche Fragen stellen, Experimente planen und neue Antworten auf wissenschaftliche Fragen finden können.

Seine Arbeit in den letzten drei Jahrzehnten konzentrierte sich auf die Schaffung einer formalen Sprache für Maschinen, um Kausalität zu ermöglichen, ähnlich wie seine Arbeit in Bayes'schen Netzwerken, die es Maschinen ermöglichten, probabilistische Assoziationen zu erzeugen. In einem seiner Artikel heißt es:

Der größte Teil des menschlichen Wissens ist eher nach kausalen als nach probabilistischen Zusammenhängen organisiert, und die Grammatik der Wahrscheinlichkeitsberechnung reicht nicht aus, um diese Zusammenhänge zu verstehen ... Aus diesem Grund betrachte ich mich nur als halb Bayesian.

Es scheint, dass Data Science nur gewinnen wird, wenn wir mehr Knabbereien haben.