
Wenn wir die heutigen Algorithmen für maschinelles Lernen mit einer Bewegung von Unwissenheit (unten) zu Bewusstsein (oben) betrachten, dann sind aktuelle Algorithmen wie ein Sprung. Nach dem Sprung gibt es eine Verlangsamung der Entwicklungsrate (Lernfähigkeit) und eine unvermeidliche Wende und einen Sturz (Umschulung). Alle Anstrengungen beschränken sich auf Versuche, so viel Kraft wie möglich auf den Sprung auszuüben, was die Sprunghöhe erhöht, die Ergebnisse jedoch nicht grundlegend verändert. Wenn wir Sprünge pumpen, erhöhen wir die Höhe, lernen aber nicht zu fliegen. Um die Technik des "kontrollierten Fliegens" zu beherrschen, müssen einige Grundprinzipien überdacht werden.
In neuronalen Netzen wird eine statische Struktur verwendet, die es nicht erlaubt, über die etablierte Lernfähigkeit der gesamten Struktur hinauszugehen. Indem wir die Größe des Netzwerks anhand einer festgelegten Anzahl von
Neuronen festlegen, begrenzen wir die Größe der Lernfähigkeit des Netzwerks, die das Netzwerk niemals umgehen kann. Die Installation einer größeren Anzahl von Neuronen beim Erstellen eines Netzwerks ermöglicht es Ihnen, die Lernfähigkeit zu erhöhen, verlangsamt jedoch die Lernzeit. Dynamische Änderungen der Netzwerkstruktur während des Trainings und die Verwendung von Binärdaten verleihen dem Netzwerk eindeutige Eigenschaften und umgehen diese Einschränkungen.
1. Dynamische Netzwerkstruktur
Das Netzwerk selbst muss Entscheidungen über seine Größe treffen. Wachsen Sie nach Bedarf in die richtige Richtung und vergrößern Sie die Größe. Wenn wir ein Netzwerk, ein Neuron, eine Schicht oder zwei, erstellen, können wir die erforderliche Trainingsfähigkeit des Netzwerks und folglich seine Größe nicht eindeutig kennen. Unser Netzwerk sollte bei Null anfangen (völlige Strukturlosigkeit) und in der Lage sein, selbständig in die richtige Richtung zu expandieren, wenn neue Trainingsdaten eintreffen.
2. Signaldämpfung
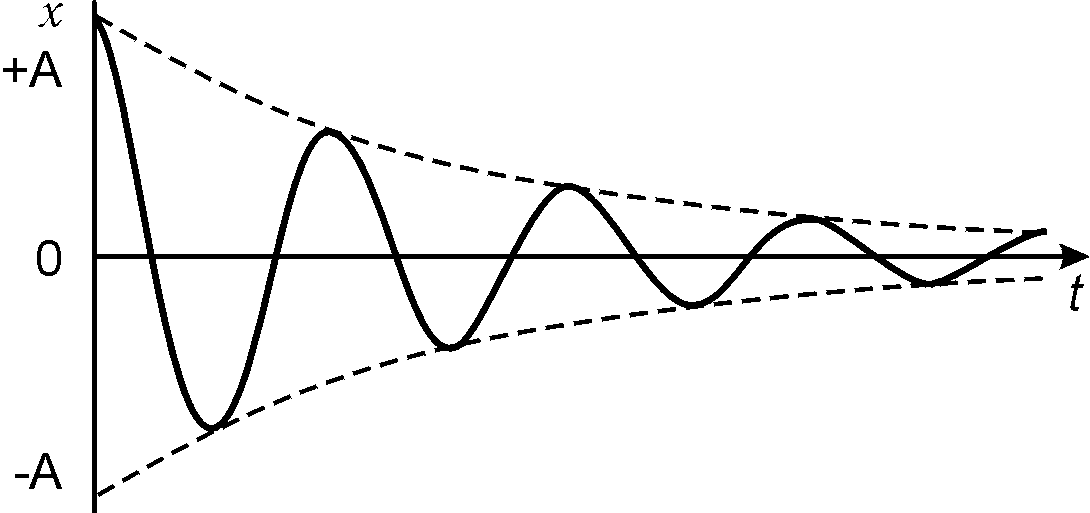
Neuronale Netze, die an der Summierung des Signals beteiligt sind, verwenden den "analogen" Berechnungsansatz. Mehrfachkonvertierungen führen zu einer Dämpfung des Signals und dessen Verlust während der Übertragung. Bei großen Netzwerkgrößen führen "analoge" Berechnungsmethoden zwangsläufig zu Verlusten. In neuronalen Netzen kann das Problem der Signaldämpfung durch wiederkehrende Netze gelöst werden, da es sich tatsächlich um eine Krücke handelt, die das Problem nur verringert, nicht aber vollständig löst. Die Lösung besteht darin, ein binäres Signal zu verwenden. Die Anzahl der Transformationen eines solchen Signals führt nicht zu dessen Dämpfung und Verlust während der Transformationen.
3. Fähigkeit zum Lernen im Netzwerk

Wenn wir die Struktur erweitern, während wir lernen, erhöhen wir ihre Lehrfähigkeit. Das Netzwerk selbst bestimmt anhand der Aufgabe, in welche Richtung es sich entwickeln soll und wie viele Neuronen zur Lösung des Problems benötigt werden. Die Netzwerkgröße beschränkt nur die Rechenleistung der Server und die Größenbeschränkungen der Festplatte.
4. Netzwerktraining
Wenn Signale von analogen zu binären Netzwerken geändert werden, besteht die Möglichkeit eines beschleunigten Lernens. Das Training bietet eine eindeutige Einstellung des Ausgangssignals. Der Lernprozess selbst verändert nur einen kleinen Teil der Neuronen und lässt einen wesentlichen Teil unverändert. Die Trainingszeit wird um ein Vielfaches reduziert und auf Änderungen in mehreren Netzwerkelementen beschränkt.
5. Netzwerkberechnung

Um das neuronale Netzwerk zu berechnen, müssen wir alle Elemente berechnen. Das Überspringen der Berechnung eines Teils der Neuronen kann zum Butterfly-Effekt führen, bei dem ein unbedeutendes Signal das Ergebnis der gesamten Berechnung verändern kann. Die Art der Binärsignale ist unterschiedlich. In jeder Phase ist es möglich, einen Teil der Daten ohne Konsequenzen von der Berechnung auszuschließen. Je größer das Netzwerk, desto mehr Elemente können wir in den Berechnungen ignorieren. Die Berechnung der Ergebnisse von Netzwerken reduziert sich auf die Berechnung einer kleinen Anzahl von Elementen bis zu Brüchen von einem Prozent des Netzwerks. Für die Berechnung sind 3,2% (32 Neuronen) mit einem Netzwerk von tausend Neuronen, 0,1% (1 Tausend) mit einer Million "Neuronen" in einem Netzwerk und 0,003% (32 Tausend) mit einem Netzwerk von einer Milliarde "Neuronen" in der Größe ausreichend. Mit zunehmender Netzwerkgröße sinkt der Prozentsatz der zur Berechnung benötigten Neuronen.
6. Interpretation der Ergebnisse
In neuronalen Netzen machen es Gewichtungen multipliziert mit Koeffizienten unmöglich, eine Signalquelle herzustellen. Alle eingehenden Signale des neuronalen Netzes beeinflussen ausnahmslos das Ergebnis und erschweren das Verständnis der Gründe, die zu seiner Bildung geführt haben. Der Einfluss von Binärsignalen auf das Ergebnis kann null, teilweise oder vollständig sein, was die Beteiligung der Quelldaten an der Berechnung eindeutig anzeigt. Mit binären Methoden zur Berechnung von Signalen können Sie die Beziehung zwischen eingehenden Daten und dem Ergebnis verfolgen und den Grad des Einflusses der Quelldaten auf die Bildung des Ergebnisses bestimmen.
All dies legt die Notwendigkeit nahe, die Ansätze für maschinelle Lernalgorithmen zu ändern. Klassische Methoden geben keine vollständige Kontrolle über das Netzwerk und ein eindeutiges Verständnis der darin ablaufenden Prozesse. Um einen „kontrollierten Flug“ zu erreichen, ist es erforderlich, die Zuverlässigkeit der Signalumwandlung innerhalb des Netzwerks und die dynamische Bildung der Struktur im laufenden Betrieb sicherzustellen.