Hallo habr Ich präsentiere Ihnen die Übersetzung des Artikels
"Eine intuitive Erklärung von Hypothesentests und P-Werten" von Joos Korstanje.
Vor ein paar Jahren habe ich meine erste freiberufliche statistische Tätigkeit für ein Obst- und Gemüselieferunternehmen ausgeübt. 24 Stunden am Tag durchliefen die Produkte der Landwirte die Qualitätskontrollabteilung, bevor sie in die Supermärkte geschickt wurden. Die Auswahl der Produkte erfolgte durch Mitarbeiter dieser Abteilung nach dem Zufallsprinzip.
Im Geschäftsbericht stellten sie fest, dass die Qualität in diesem Jahr niedriger ist als in der Vergangenheit: Die Differenz betrug etwa einen halben Punkt auf einer Skala von 1 bis 10.
Dann haben sie mich eingeladen. Ich musste die Frage beantworten:
Sind diese 0,5 Punkte ein signifikanter Unterschied?Wenn Sie die Statistiken nicht kennen, scheint Ihnen diese Frage seltsam. Aber keine Sorge: Der Zweck dieses Artikels ist es, Ihnen zu zeigen, wie Sie diese Frage mithilfe von Hypothesentests, auch als statistische Inferenz bezeichnet, beantworten können.
Das Spiel der Zahlen: der Beitrag eines Apfels
Stellen Sie sich vor, Sie überprüfen einen Apfel auf Gut oder Böse, indem Sie eine zufällige Auswahl von Äpfeln aus einer sehr großen Schachtel mit Äpfeln verwenden. In der Abbildung unten sehen wir den tatsächlichen Einfluss der Stichprobengröße auf die Messungen: Die Auswirkung eines Apfels ist für kleine Stichproben sehr signifikant und nimmt mit zunehmender Stichprobengröße immer weniger ab.
Der Beitrag eines Apfels hängt von der Stichprobengröße ab.Das Verständnis der Auswirkung der Stichprobengröße ist die erste Grundlage für das Verständnis des Hypothesentests. Wir können anfangen zu argumentieren, dass 0,5 auf 2 Äpfeln wie ein Unterschied von 1 Apfel ist, sehr klein. Aber für 100 Äpfel bedeutet 0,5 einen Unterschied von 50 Äpfeln: ein sehr großer Unterschied!
Für kleine Stichproben sind 0,5 Punkte ein kleiner Unterschied, für große Stichproben 0,5 ist dies ein großer Unterschied.Wie groß die Stichprobe sein sollte: Hypothesentest und Signifikanz als Antwort
Es gibt verschiedene Möglichkeiten, diese Frage zu beantworten, aber in diesem Artikel werde ich auf statistische Inferenz oder Hypothesentests eingehen.
Beim Testen von Hypothesen handelt es sich um eine Reihe statistischer Methoden, mit denen untersucht wird, wie die Stichprobe beobachteter Objekte verwendet werden kann, um eine vordefinierte Hypothese zu akzeptieren oder abzulehnen. Das Testen von Hypothesen wird verwendet, um viele Probleme zu lösen, hauptsächlich in der wissenschaftlichen Forschung und als Schlüsselmethode im Online-Marketing (A \ B-Testen).
Mathematiker haben einen Hypothesentest so entwickelt, dass es ein bestimmtes Verfahren gibt, um die Wahrheit zu finden.
Mit dem Testen von Hypothesen können Sie Hypothesen nur testen, aber nicht entwickeln.Aus der Schachtel mit 100 Äpfeln (nennen wir es die Population) nehmen wir eine Stichprobe von 8 Äpfeln. In diesem Jahr waren von 8 Äpfeln 5 faul (62%), und in der Stichprobe im letzten Jahr waren von 8 Äpfeln nur 4 faul (50%). Wir wollen einen Hypothesentest verwenden, um festzustellen, ob der Prozentsatz an faulen Äpfeln in diesem Jahr höher ist als im letzten Jahr.
Hypothesentests sind eine mathematische Alternative zur Populationsmessung. Dank dieser Berechnungen können wir die Messungen einer kleinen Stichprobe auf eine große Population verallgemeinern. Also machen wir weniger Arbeit.
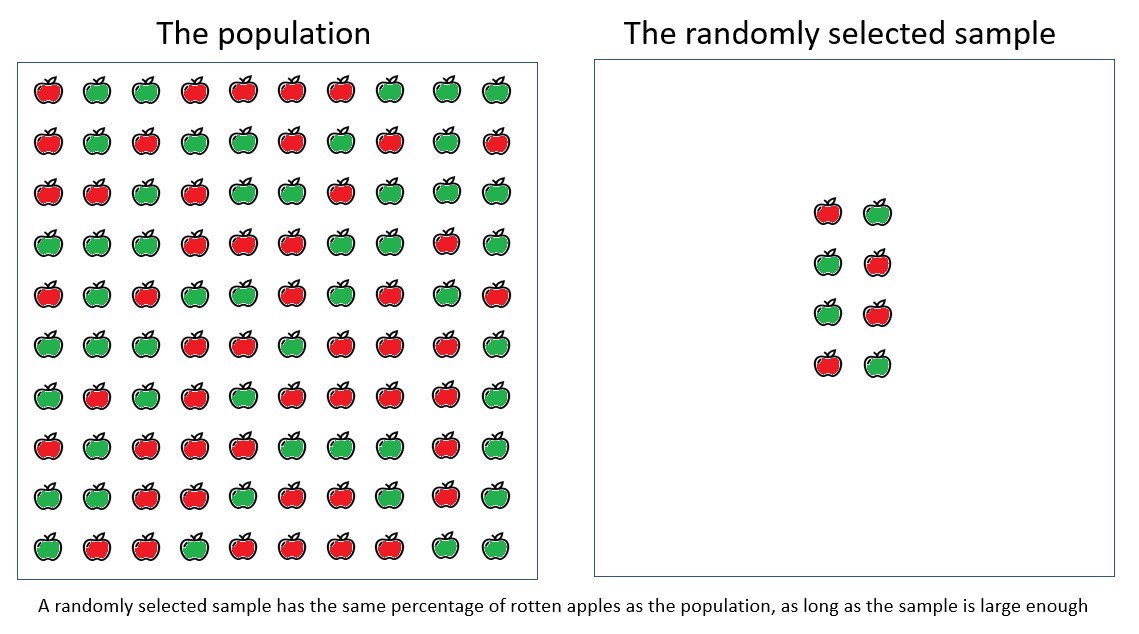
Eine zufällig ausgewählte Stichprobe enthält den gleichen Prozentsatz fauler Äpfel wie die allgemeine Bevölkerung, vorausgesetzt, die gesammelte Stichprobe ist groß genug.
Mathematiker haben einen Weg gefunden, um die Schlussfolgerung basierend auf der Stichprobe auf die allgemeine Bevölkerung zu verallgemeinern.
Diese Methode beginnt mit der Formulierung einer klaren Forschungshypothese. Leider funktioniert Mathematik nur, wenn wir bereits eine Vorstellung davon haben, was wir testen möchten.
Die Haupthypothese für unser Beispiel:
Der Anteil fauler Äpfel an der Gesamtbevölkerung ist in diesem Jahr höher als in der Vergangenheit.Tatsächlicher Hypothesentest
Die Mathematik des Hypothesentests bildet ein Gleichgewicht zwischen dem Ergebnis der Messung der Probe und der Anzahl der Beobachtungen. Das Ergebnis ist ein p-Wert.Diese Berechnungen basieren auf Verteilungen: Für fast jede imaginäre Situation wurde ein mathematisches Gesetz abgeleitet, das das erwartete Ergebnis beschreibt.
Für Ja / Nein-Fragen, wie die Frage nach unseren faulen Äpfeln (faul / nicht faul), gilt das Münzwurfgesetz. Dies ist das einfachste Beispiel eines mathematischen Gesetzes: 50% Schwänze, 50% Adler.
Es kann auch sehr einfach als mathematische Standardverteilung dargestellt werden, die über die Wahrscheinlichkeit von Beobachtungen Auskunft gibt. Zum Beispiel haben 7 Adler 10 Münzwürfe verloren. Dies wird als Binomialverteilung bezeichnet und kann wie folgt dargestellt werden:
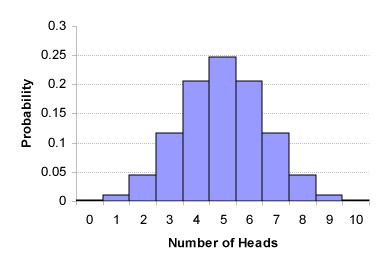Binomialverteilung von 10 Münzwürfen.In diesem Artikel werde ich mich weit von der harten Mathematik entfernen, aber es ist wichtig zu wissen, dass wir mathematische Formeln verwenden können, um zu bewerten, ob der beobachtete Prozentsatz weit vom erwarteten Prozentsatz entfernt ist.
Am Ende dieses Artikels werde ich Ihnen eine Liste häufig verwendeter Hypothesentestformeln für verschiedene Fälle geben und anschließend erklären, wie man sie verwendet. Aber zuerst erkläre ich die Interpretation des Hypothesentests.
Ergebnis des Hypothesentests: p-Wert
Hinter dem Testen von Hypothesen steht ein mathematisches Gleichgewicht zwischen den beobachteten Werten und der Stichprobengröße. Am Ende der Berechnungen wird mit jeder vorhandenen Option zum Testen von Hypothesen eine standardisierte Punktzahl erstellt, mit der Sie das Ergebnis auch dann vergleichen können, wenn die Mathematik nicht exakt gleich ist.
Der P-Wert ist eine Standardmethode, um ein Hypothesentestergebnis zu formulieren und in anderen Tests zu verwenden.
Der P-Wert ist eine Zahl zwischen 0 und 1, die uns sagt, ob der Unterschied zwischen unseren Beobachtungen der Proben und unseren Hypothesen sehr unterschiedlich ist. Der Referenzwert beträgt 0,05.
Der Unterschied ist statistisch signifikant, wenn der p-Wert kleiner als 0,05 ist.
Und der Unterschied ist statistisch nicht signifikant, wenn der p-Wert größer als 0,05 ist.
Beispiel 1:
Wir haben 10 Münzwürfe gemacht.
Unsere Hypothese: Wir erwarten 5 Schwänze.
Unsere Beobachtungen: Wir haben 6 Schwänze.
Die Berechnung des p-Wertes ergab 0,518, was mehr als 0,05 ist.
Unser Fazit: Der Unterschied ist statistisch nicht signifikant.
Unsere Interpretation: Das Ergebnis stimmt mit der Hypothese überein.
Beispiel 2:
Wir haben 10 Münzwürfe gemacht
Unsere Hypothese: Wir erwarten 5 Schwänze.
Unser Ergebnis: Wir haben 10 Schwänze.
Unser p-Wert ist 0.0, was weniger als 0.05 ist.
Unser Fazit: Der Unterschied ist statistisch signifikant
Unsere Interpretation: Das Ergebnis stimmt nicht mit der Hypothese überein.
Beispiel 3:
Wir haben 10 Äpfel geprüft.
Unsere Hypothese: Wir erwarten 1 faulen Apfel.
Unser Ergebnis: Wir haben 1 faule Äpfel bekommen.
Unser p-Wert ist 1.0, was mehr als 0.05 ist.
Unser Fazit: Der Unterschied ist statistisch nicht signifikant
Unsere Interpretation: Das Ergebnis stimmt mit der Hypothese überein.
Beispiel 4:
Wir haben 10 Äpfel geprüft.
Unsere Hypothese: Wir erwarten 1 faulen Apfel.
Unser Ergebnis: Wir haben 5 faule Äpfel.
Unser p-Wert ist 0,0114, was weniger als 0,05 ist.
Unser Fazit: Der Unterschied ist statistisch signifikant
Unsere Interpretation: Das Ergebnis stimmt nicht mit der Hypothese überein.
Fazit
In diesem Artikel gab ich eine intuitive Interpretation der allgemeinen Struktur von statistischen Fehlern oder Hypothesentests. Ich hoffe, dass Sie das Testen von Hypothesen jetzt besser verstehen und wie nützlich es für Sie sein kann.
Ich habe mich nicht mit mathematischen Beweisen und spezifischen Details befasst. Die folgende Tabelle enthält eine Liste der häufigsten Hypothesentests, die ich für weitere Studien empfehle.
Eine Liste mit alternativen Hypothesen für einige Hypothesentests.
Ich hoffe, dieser Artikel wird Ihnen von Nutzen sein, und ich wünsche Ihnen viel Glück bei der weiteren Erforschung von Hypothesentests.