Täglich werden im globalen Web Artikel zu den beliebtesten und am häufigsten verwendeten Algorithmen für maschinelles Lernen zur Lösung verschiedener Probleme veröffentlicht. Darüber hinaus wandert die Basis dieser Artikel, deren Form an der einen oder anderen Stelle geringfügig geändert wurde, von einem Datenforscher zum anderen. Darüber hinaus werden alle diese Arbeiten durch ein allgemein anerkanntes, unbestreitbares Postulat vereint: Die Anwendung des einen oder anderen Algorithmus für maschinelles Lernen hängt von der Größe und Art der verfügbaren Daten und der vorliegenden Aufgabe ab.
Darüber hinaus betonen besonders erfahrene Datenforscher:
„Die Wahl einer Bewertungsmethode sollte teilweise von Ihren Daten abhängen und davon, welches Modell Ihrer Meinung nach gut sein sollte.“ („Data Science: Insider-Informationen für Anfänger. Einschließlich R-Sprache (von Cathy O'Neill, Rachel Shutt) .
Mit anderen Worten, ein Statistiker / Datenforscher sollte nicht nur Erfahrung auf dem Fachgebiet haben, sondern auch ein breites Spektrum an unterschiedlichen Kenntnissen:
„Ein Datenforscher verfügt über Kenntnisse in den folgenden Bereichen: Mathematik, Statistik, Computertechnik, maschinelles Lernen, Visualisierung, Mittel zum Datenaustausch ... “ (aus demselben Buch). Nur durch gründliches Laden von Wissen aus den oben genannten Bereichen in den Kopf kann man sich dem maschinellen Lernen nähern und Lösungen für die angegebenen Probleme finden.
Für mich ist dieser Anfang durchaus geeignet für ein reguläres anderthalb Kilogramm schweres Buch über Data Science oder einen wissenschaftlichen Artikel über Horrorgeschichten mit nachfolgenden „wertlosen“ zweistöckigen Formeln, Symbolen und Kringeln, die für Anfänger auf dem Gebiet des maschinellen Lernens einen deprimierenden und schwerwiegenden Einfluss haben, und zwar zufällig interesse an dieser richtung unerfahrene leser, die nicht mit "notwendigen kenntnissen" belastet sind. Darüber hinaus verstärkt die zehnte Runde derselben Artikel über die zehn beliebtesten Algorithmen
für maschinelles Lernen (
zum Beispiel ) nur den auferlegten Effekt.
Bei habr zeichneten sie sich außerdem aus :
„Die Antwort auf die Frage: Welche Art von Algorithmus für maschinelles Lernen soll ich verwenden?“ Klingt immer so: „Abhängig von den Umständen“. Die Wahl des Algorithmus hängt von der Menge, Qualität und Art der Daten ab. Es hängt davon ab, wie Sie das Ergebnis verwalten. Dies hängt davon ab, wie die Anweisungen für den Computer, der sie implementiert, aus dem Algorithmus erstellt wurden, und auch davon, wie viel Zeit Sie haben. Selbst die erfahrensten Datenanalysten werden Ihnen nicht sagen, welcher Algorithmus besser ist, bis sie es versuchen. “Zweifellos sind all diese Kenntnisse sowie Ausdauer und Interesse notwendig und nützlich, um nicht nur auf dem Weg zum Verständnis des maschinellen Lernens, sondern auch in vielen anderen Bereichen gute Ergebnisse zu erzielen. Darüber hinaus erleichtern sie das Verständnis, dass Algorithmen für maschinelles Lernen (im Folgenden als Algorithmen bezeichnet) weit von einem Dutzend entfernt sind. Dies ist aber erst später, mit unabhängigem Studium.
Mein Ziel ist es, den Leser mit den am häufigsten verwendeten Algorithmen aus praktischer und zugänglicher Sicht bekannt zu machen. (Die Tatsache, dass ich kein Programmierer und darüber hinaus kein Mathematiker bin!) Sollte das Interesse an der Erzählung unterstreichen. Ingenieurausbildung plus Erfahrung im „Fachwachstum“ von 10 Jahren (nur eine Art magische Zahl) ) - wie gesagt, und all meine Sachen, all mein Gepäck, mit dem ich direkt zum maschinellen Lernen übergegangen bin. Dank der Erfahrungen in der Ölindustrie wurden sofort Ideen für den Einsatz künstlicher neuronaler Netze und maschineller Lernalgorithmen gefunden (gelesen - es waren notwendig) Datensätze.) Alles, was übrig blieb, war zu beschäftigen Scarlet - lernen Sie, die Daten zu verdrehen und zu verdrehen, um sie korrekt an die Eingabe des "Programms" und den tatsächlich zu wählenden Algorithmus zu übergeben. Und dann in einem Teufelskreis / f "Die Abenteuer von Funtik"), - aber ich habe es trotzdem geschafft, mir Notizen zu machen, und wenn Interesse besteht, werde ich in Zukunft weitere Nachrichten veröffentlichen.)
Daher schlage ich vor, mich der „Bearbeitung“ zu nähern: Warum nicht Ihren vorhandenen Datensatz (in den Beispielen laden Sie Datensätze, die leicht zu trainieren sind) auf einmal vielen Algorithmen zuzuführen und anhand der Ergebnisse zu entscheiden, welchen Sie genauer beachten sollten anschließende sorgfältige Untersuchung und Auswahl der optimalen Parameter, die das Ergebnis verbessern. Darüber hinaus ist der Hauptwert der oben diskutierten Methode, dass ihre Ergebnisse die Frage beantworten, welchen Wert Ihr Datensatz hat:
"Lösen Sie zunächst das Problem und stellen Sie sicher, dass Sie etwas zu optimieren haben" (auch von einigen) dann ging die beharrliche Statistik, "Respekt" für ihn, guter Rat!).
Wie wird es gemacht?
Es ist bekannt, dass sich der Großteil der mit Hilfe von Algorithmen gelösten Probleme auf die Probleme der Klassifikation (Klassifikation) und der Regressionsanalyse (Vorhersageanalyse) bezieht. Mit
Klassifizierung ist eine stetige Differenzierung von Beobachtungseinheiten (Instanzen) eines Datensatzes zu einer bestimmten Kategorie (Klasse) gemäß den Trainingsergebnissen gemeint.
Die Regressionsanalyse ist eine Reihe statistischer Methoden und Verfahren zur Beurteilung der Beziehung zwischen Variablen [
Statistics: Textbook / Ed. prof. M.R. Efimova. - M .: INFRA-M, 2002 ]. Der Zweck der Regressionsanalyse besteht darin, den Wert einer kontinuierlichen Ausgabevariablen aus den Werten der Eingabevariablen zu ermitteln [
Link ].
Wir lassen die Tatsache aus, dass der Regressionsanalyse zwei verschiedene Methoden zur Verfügung stehen - Vorhersagemodellierung und Vorhersage. Wir stellen nur fest, dass bei Vorliegen einer Zeitreihe (Zeitreihendaten) unter Verwendung eines auf einem expliziten Trend beruhenden Regressionsmodells unter Berücksichtigung der Stationarität (Konstanz) Prognosen durchgeführt werden können. Wenn sich die Bedingungen für die Bildung von Ebenen der Zeitreihen ändern, das heißt, ein instationärer Prozess nicht beobachtet wird, liegt es an der prädiktiven Modellierung. Insbesondere für die vollständige Beherrschung von ML schlage ich vor, diesen Artikel auf Englisch zu lesen:
Link . Wenn sich darüber eine Diskussion ergibt, nehme ich gerne daran teil.
Da in den Beispielen in diesem Artikel keine Zeitreihen verwendet werden, bezieht sich der Begriff
Prognose auf die
prädiktive Analyse .
Um die Probleme der Klassifizierung und Vorhersage zu lösen, ist eine ganze Reihe von Algorithmen geeignet, von denen einige später betrachtet werden. Der Einfachheit halber wird der nachfolgende Text in zwei Teile unterteilt: Im ersten Teil werden die gängigsten Klassifizierungsalgorithmen betrachtet, im zweiten Teil die Algorithmen für die Regressionsanalyse. Für jeden Teil wird ein "Spielzeug"
-Datensatz aus
der Scikit-Lernbibliothek (v0.21.3) angezeigt:
Ziffern-Datensatz (Klassifizierung) und
Boston-Hauspreis-Datensatz (Regression) sowie Links zu jedem Algorithmus der Scikit-Lernbibliothek zur Selbstprüfung und eventuell zum Lernen.
Alle Codebeispiele werden in der
IDE Spyder 3.3.3-Konsole unter Python 3.7.3 ausgeführt.
Klassifizierungsproblem
Zuerst importieren wir die notwendigen Module und Funktionen, die wir zur Lösung des Problems der Datenklassifizierung verwenden werden:
Laden Sie den Datensatz 'digits' direkt aus
dem Modul 'sklearn.datasets' herunter :
IDE Spyder bietet ein praktisches Tool "Variablen-Manager", das zu jedem Zeitpunkt des Lernens von Maschinenlernen nützlich ist (zumindest für mich), wie
andere "Tricks" :
Führen Sie den Code aus. Klicken Sie in der Konsole "Variablenmanager" auf die
Datensatzvariable . Das folgende Wörterbuch wird angezeigt:
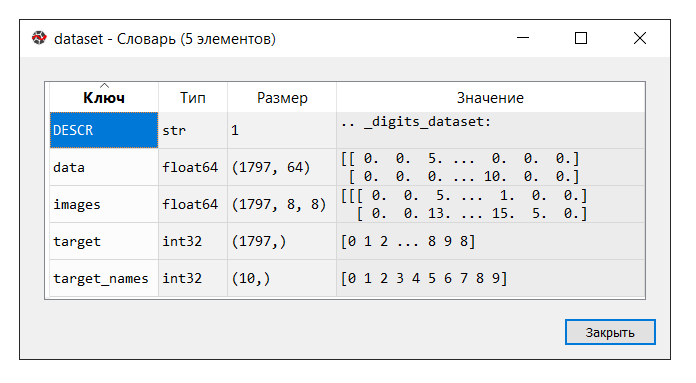
Die Beschreibung des Datensatzes lautet wie folgt:
In diesem Beispiel benötigen wir den Schlüssel "images" nicht. Daher weisen wir die Variable "data" der Variablen
X zu , die ein mehrdimensionales NumPy-Array mit einer Reihe von Attributen mit einer Größe von 1797 Zeilen mal 64 Spalten und die Variable
Y "target", ein mehrdimensionales NumPy-Array mit jeweils einer Markierung Zeichenfolge.
Als nächstes unterteilen wir den Datensatz in Trainings- und Testteile, konfigurieren die Parameter für die Auswertung der Algorithmen (Kreuzvalidierung wird verwendet [
eins ,
zwei ]) und definieren die Metrik 'Genauigkeit' im Parameter 'Bewertung' [
Link ]. Die Genauigkeit ist der Anteil korrekt klassifizierter Objekte an der Gesamtzahl der Objekte. Je näher das Ergebnis an 1 liegt, desto besser ist [
link ]. Darüber hinaus wurde in einem der Bücher festgestellt, dass die Ergebnisse ab 0,95 (oder 95%) als ausgezeichnet gelten.
Lassen Sie die Variablen
X_train und
Y_train für Trainingszwecke verwenden,
X_test und
Y_test für die Entwicklung von Prognosewerten. In diesem Fall ist die Variable
Y_test nicht an der Berechnung der Prognose beteiligt. Bei Verwendung der "Score" -Methode, die für jeden der unten dargestellten Algorithmen gleich ist, werden die richtigen Antworten anhand der "Genauigkeit"
-Metrik berechnet. Auf diese Weise können wir beurteilen, wie der Algorithmus die Aufgabe bewältigt. Ich behaupte nicht, es ist für unseren Teil so menschlich gemein, das Auto nicht mit den richtigen Antworten aufzufordern, aber wie kann man sonst seine Leistung überprüfen?
Unten finden Sie eine Liste der Algorithmen, mit denen wir den Datensatz füttern. Basierend auf den Ergebnissen der Berechnungen werden wir schließen, welcher Algorithmus (welcher der Algorithmen) die größte Effizienz zeigt. Diese Methode kann durchaus als
"Blitz-Test von Algorithmen für maschinelles Lernen" (im Folgenden - Blitz-Test) bezeichnet werden.
Der Einfachheit halber werden Informationen neben jedem Algorithmus abgekürzt. Es ist zu beachten, dass die Einstellungen jedes Algorithmus mit Ausnahme einiger Punkte standardmäßig (Standard) akzeptiert werden, um gleiche Bedingungen zu gewährleisten.
Lineare Algorithmen:
- Logistische Regression * /
Logistische Regression (LR)
* Das Wort "Regression" kann verwirrend sein. Vergessen Sie jedoch nicht, dass „Logistic Regression“ ein Klassifizierungsalgorithmus ist-
Lineare Diskriminanzanalyse (LDA)
Nichtlineare Algorithmen:
- Methode der nächstgelegenen Nachbarn (Klassifizierung) /
K-Neighbours Classifier ('KNN')
-
Entscheidungsbaumklassifikator ('CART')
-
Naive Bayes Classifier ('NB')
-
Lineare Stützvektorklassifizierungsmethode (Klassifizierung) /
Lineare Stützvektorklassifizierung ('LSVC')
-
Support-Vektor- Methode (Klassifikation) /
C-Support-Vektor-Klassifikation ('SVC')
Künstlicher neuronaler Netzwerkalgorithmus:
-
Multilayer Perceptron /
Multilayer Perceptrons ('MLP')
Ensemble-Algorithmen:
- Absacken (Klassifizierung) /
Absackklassifizierer ('BG') (Absacken = Bootstrap-Aggregation)
-
Zufällige Waldklassifikation ('RF')
-
Extra Trees Classifier ('ET')
- AdaBoost (Klassifizierung) /
AdaBoost Classifier ('AB') (AdaBoost = Adaptive Boosting)
- Gradient Boosting (Klassifizierung) /
Gradient Boosting Classifier ('GB')
Daher enthält die Liste der "Modelle" die folgenden Modelle:
models = [] models.append(('LR', LogisticRegression())) models.append(('LDA', LinearDiscriminantAnalysis())) models.append(('KNN', KNeighborsClassifier())) models.append(('CART', DecisionTreeClassifier())) models.append(('NB', GaussianNB())) models.append(('LSVC', LinearSVC())) models.append(('SVC', SVC())) models.append(('MLP', MLPClassifier())) models.append(('BG', BaggingClassifier(n_estimators=n_estimators))) models.append(('RF', RandomForestClassifier(n_estimators=n_estimators))) models.append(('ET', ExtraTreesClassifier(n_estimators=n_estimators))) models.append(('AB', AdaBoostClassifier(n_estimators=n_estimators, algorithm='SAMME'))) models.append(('GB', GradientBoostingClassifier(n_estimators=n_estimators)))
Wie bereits erwähnt, wird die Wirksamkeit jedes Algorithmus durch Kreuzvalidierung bewertet. Als Ergebnis wird eine Nachricht angezeigt (msg - Abkürzung von message), die die folgenden Informationen enthält: Modellname in Form einer Abkürzung, durchschnittliche Punktzahl von 10-facher Kreuzvalidierung der Trainingsdaten (metrische Genauigkeit), Standardabweichung in Klammern sowie den Wert der Genauigkeitsmetrik für die Testdaten.
Nach dem Ausführen des Codes erhalten wir die folgenden Ergebnisse:
LR: train = 0.957 (0.014) / test = 0.948 LDA: train = 0.951 (0.014) / test = 0.946 KNN: train = 0.985 (0.013) / test = 0.981 CART: train = 0.843 (0.033) / test = 0.830 NB: train = 0.819 (0.048) / test = 0.806 LSVC: train = 0.942 (0.017) / test = 0.928 SVC: train = 0.343 (0.079) / test = 0.342 MLP: train = 0.972 (0.012) / test = 0.961 BG: train = 0.952 (0.021) / test = 0.941 RF: train = 0.968 (0.017) / test = 0.965 ET: train = 0.980 (0.010) / test = 0.975 AB: train = 0.827 (0.049) / test = 0.823 GB: train = 0.964 (0.013) / test = 0.968
Spannendiagramm (
„Box mit Schnurrbart“ ) (Box-and-Whiskers-Diagramm oder -Diagramm, Box-Diagramm):
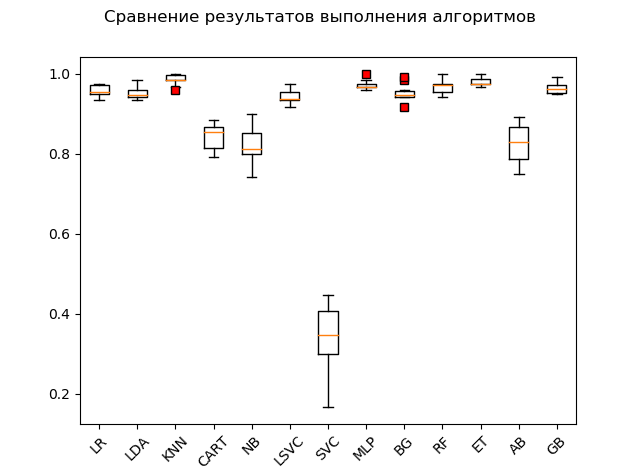
Als Ergebnis eines Blitztests mit „Rohdaten“ ist klar, dass die Algorithmen „KNN“ (k-nächste Nachbarn), „ET“ (Extrabäume), „GB“ (Gradient „Boosting“) die effektivsten für die Testdaten waren. RF (Random Forest) und MLP (Multilayer Perceptron):
KNN: train = 0.985 (0.013) / test = 0.981 ET: train = 0.980 (0.010) / test = 0.975 GB: train = 0.964 (0.013) / test = 0.968 RF: train = 0.968 (0.017) / test = 0.965 MLP: train = 0.972 (0.012) / test = 0.961 LR: train = 0.957 (0.014) / test = 0.948 LDA: train = 0.951 (0.014) / test = 0.946 BG: train = 0.952 (0.021) / test = 0.941 LSVC: train = 0.942 (0.017) / test = 0.928 CART: train = 0.843 (0.033) / test = 0.830 AB: train = 0.827 (0.049) / test = 0.823 NB: train = 0.819 (0.048) / test = 0.806 SVC: train = 0.343 (0.079) / test = 0.342
Viele Algorithmen sind jedoch sehr wählerisch in Bezug auf die bereitgestellten Daten. Daher ist einer der notwendigen Schritte die sogenannte vorläufige Datenaufbereitung (Datenvorverarbeitung [
Link ]).
Es kommt jedoch vor, dass der Algorithmus die besten Ergebnisse ohne Vorverarbeitung anzeigt. Daher die folgende Empfehlung: Nehmen Sie mehrere Transformationen des Originaldatensatzes in den Blitz-Test auf und vergleichen Sie nach Durchführung der Berechnungen die Ergebnisse, um das Wesentliche des Problems als Ganzes zu erfassen.
Die am häufigsten verwendeten Methoden zur vorläufigen Datenaufbereitung sind:
-
Normung;
-
Skalierung (der Standardbereich ist [0, 1]);
-
NormalisierungDiese Vorgänge mit anschließender Auswertung können mit dem
Pipeline- Tool automatisiert und auf das Förderband gelegt werden.
Ein Code-Snippet mit Standardisierung der Quelldaten sieht wie folgt aus:
Beachten Sie das Hinzufügen von '_SS' (kurz für StandardScaler) zur Liste der Namen. Dies geschieht, um die Ergebnisse nicht zu stapeln und um sie nach der Durchführung der Konvertierungen bequem mit dem "Variablenmanager" anzuzeigen.
Das Ausführen eines Code-Snippets führt zu folgenden Ergebnissen:
SS_LR: train = 0.958 (0.015) / test = 0.949 SS_LDA: train = 0.951 (0.014) / test = 0.946 SS_KNN: train = 0.968 (0.023) / test = 0.970 SS_CART: train = 0.853 (0.036) / test = 0.835 SS_NB: train = 0.756 (0.046) / test = 0.751 SS_LSVC: train = 0.945 (0.018) / test = 0.941 SS_SVC: train = 0.976 (0.015) / test = 0.990 SS_MLP: train = 0.976 (0.012) / test = 0.973 SS_BG: train = 0.947 (0.018) / test = 0.948 SS_RF: train = 0.973 (0.016) / test = 0.970 SS_ET: train = 0.980 (0.012) / test = 0.975 SS_AB: train = 0.827 (0.049) / test = 0.823 SS_GB: train = 0.964 (0.013) / test = 0.968
Schnurrbart-Box (StandardScaler):
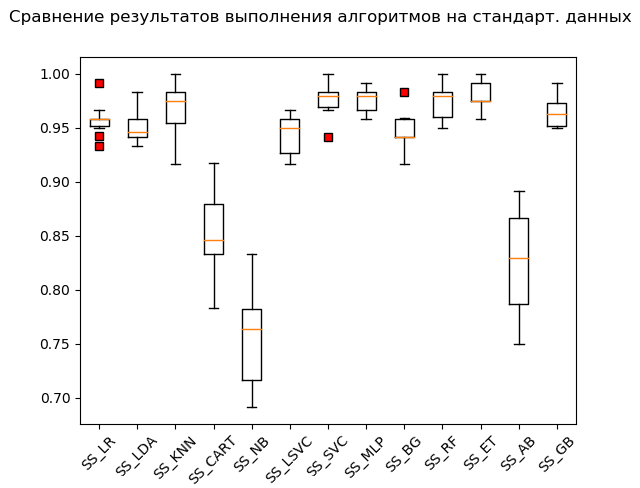
Nach den Ergebnissen der Berechnung für standardisierte Daten wurden die folgenden Algorithmen führend:
SS_SVC: train = 0.976 (0.015) / test = 0.990 SS_ET: train = 0.980 (0.012) / test = 0.975 SS_MLP: train = 0.976 (0.012) / test = 0.973 SS_KNN: train = 0.968 (0.023) / test = 0.970 SS_RF: train = 0.973 (0.016) / test = 0.970 SS_GB: train = 0.964 (0.013) / test = 0.968 SS_LR: train = 0.958 (0.015) / test = 0.949 SS_BG: train = 0.947 (0.018) / test = 0.948 SS_LDA: train = 0.951 (0.014) / test = 0.946 SS_LSVC: train = 0.945 (0.018) / test = 0.941 SS_CART: train = 0.853 (0.036) / test = 0.835 SS_AB: train = 0.827 (0.049) / test = 0.823 SS_NB: train = 0.756 (0.046) / test = 0.751
Wie sie sagen, von Lumpen zu Reichtum: Die Support-Vektor-Methode (SVC), die von standardisierten Daten gespeist wird, hat den Rest erledigt und ein hervorragendes Ergebnis erzielt. Bei der „manuellen“ Überprüfung, bei der die Werte der Variablen
Y_test und
predictions_SS [6] verglichen wurden, hat der Algorithmus nicht nur einige Werte
gekaut .
Als nächstes wird derselbe Code für die Funktionen MinMaxScaler (Skalierung) und Normalizer (Normalisierung) ausgeführt. Ich werde im Artikel nicht den vollständigen Code angeben. Sie können es von meinem Repository auf GitHub herunterladen:
Link .
Denken Sie daran, eine Weile zu hängen und über sich selbst zu lachen, nur für Bildungszwecke! :)
Nachdem wir den gesamten Code durchgearbeitet haben, erhalten wir die folgenden Ergebnisse:
LR: train = 0.957 (0.014) / test = 0.948 LDA: train = 0.951 (0.014) / test = 0.946 KNN: train = 0.985 (0.013) / test = 0.981 CART: train = 0.843 (0.033) / test = 0.830 NB: train = 0.819 (0.048) / test = 0.806 LSVC: train = 0.942 (0.017) / test = 0.928 SVC: train = 0.343 (0.079) / test = 0.342 MLP: train = 0.972 (0.012) / test = 0.961 BG: train = 0.952 (0.021) / test = 0.941 RF: train = 0.968 (0.017) / test = 0.965 ET: train = 0.980 (0.010) / test = 0.975 AB: train = 0.827 (0.049) / test = 0.823 GB: train = 0.964 (0.013) / test = 0.968 SS_LR: train = 0.958 (0.015) / test = 0.949 SS_LDA: train = 0.951 (0.014) / test = 0.946 SS_KNN: train = 0.968 (0.023) / test = 0.970 SS_CART: train = 0.853 (0.036) / test = 0.835 SS_NB: train = 0.756 (0.046) / test = 0.751 SS_LSVC: train = 0.945 (0.018) / test = 0.941 SS_SVC: train = 0.976 (0.015) / test = 0.990 SS_MLP: train = 0.976 (0.012) / test = 0.973 SS_BG: train = 0.947 (0.018) / test = 0.948 SS_RF: train = 0.973 (0.016) / test = 0.970 SS_ET: train = 0.980 (0.012) / test = 0.975 SS_AB: train = 0.827 (0.049) / test = 0.823 SS_GB: train = 0.964 (0.013) / test = 0.968 MMS_LR: train = 0.961 (0.013) / test = 0.953 MMS_LDA: train = 0.951 (0.014) / test = 0.946 MMS_KNN: train = 0.985 (0.013) / test = 0.981 MMS_CART: train = 0.850 (0.027) / test = 0.840 MMS_NB: train = 0.796 (0.045) / test = 0.786 MMS_LSVC: train = 0.964 (0.012) / test = 0.958 MMS_SVC: train = 0.963 (0.016) / test = 0.956 MMS_MLP: train = 0.972 (0.011) / test = 0.963 MMS_BG: train = 0.948 (0.024) / test = 0.946 MMS_RF: train = 0.973 (0.014) / test = 0.968 MMS_ET: train = 0.983 (0.010) / test = 0.981 MMS_AB: train = 0.827 (0.049) / test = 0.823 MMS_GB: train = 0.963 (0.013) / test = 0.968 N_LR: train = 0.938 (0.020) / test = 0.919 N_LDA: train = 0.952 (0.013) / test = 0.949 N_KNN: train = 0.981 (0.012) / test = 0.985 N_CART: train = 0.834 (0.028) / test = 0.825 N_NB: train = 0.825 (0.043) / test = 0.805 N_LSVC: train = 0.960 (0.014) / test = 0.953 N_SVC: train = 0.551 (0.053) / test = 0.586 N_MLP: train = 0.963 (0.018) / test = 0.946 N_BG: train = 0.949 (0.016) / test = 0.938 N_RF: train = 0.973 (0.015) / test = 0.970 N_ET: train = 0.982 (0.012) / test = 0.980 N_AB: train = 0.825 (0.040) / test = 0.820 N_GB: train = 0.953 (0.022) / test = 0.956
'Top 5' Ergebnisse:
SS_SVC: train = 0.976 (0.015) / test = 0.990 N_KNN: train = 0.981 (0.012) / test = 0.985 KNN: train = 0.985 (0.013) / test = 0.981 MMS_KNN: train = 0.985 (0.013) / test = 0.981 MMS_ET: train = 0.983 (0.010) / test = 0.981
Entsprechend den Ergebnissen eines Blitz-Tests von Algorithmen für maschinelles Lernen zur Lösung des Klassifizierungsproblems des 'Ziffern'-Datensatzes sind die am besten geeigneten Algorithmen für maschinelles Lernen: die Methode der nächsten k-Nachbarn (' KNN '), die Unterstützungsvektormethode (' SVC ') und Extrabäume ('ET'). Bei diesen Algorithmen sollte der Weiterentwicklung der Ergebnisse zur Steigerung der Effizienz der Berechnungen größere Aufmerksamkeit gewidmet werden. Alles, wie sie sagen, ist lösbar.
Fahren Sie mit dieser erhöhten Note nahtlos mit dem zweiten Teil fort.
Prognoseproblem
Wir bewegen uns auf dem Daumen:
Führen Sie den Code aus und beschäftigen Sie sich mit dem Wörterbuch. Beschreibung und Schlüssel lauten wie folgt:
Wir weisen den Schlüssel 'data' der Variablen
X zu , die ein mehrdimensionales NumPy-Array mit einer Reihe von Attributen ist, 506 Zeilen zu 13 Spalten dimensioniert, und der Variablen
Y - 'target', einem mehrdimensionalen NumPy-Array mit einem Marker für jede Zeile.
Wir unterteilen den Datensatz in Trainings- und Testteile, konfigurieren die Parameter zur Auswertung der Algorithmen. Im Parameter 'Scoring' setzen wir eine der für die Regressionsanalyse üblichen
Metriken 'r2' :
R2 - Bestimmungskoeffizient - Dies ist der Anteil der Varianz der abhängigen Variablen, der durch das betreffende Modell erklärt wird (
Link ).
„Der Bestimmungskoeffizient für ein Modell mit einer Konstanten nimmt Werte von 0 bis 1 an. Je näher der Koeffizient an 1 liegt, desto stärker ist die Abhängigkeit. Bei der Bewertung von Regressionsmodellen wird dies so interpretiert, dass das Modell mit Daten abgeglichen wird. Für akzeptable Modelle wird angenommen, dass der Bestimmungskoeffizient mindestens 50% betragen sollte (in diesem Fall übersteigt der Koeffizient der Mehrfachkorrelation 70% Modulo). Modelle mit einem Bestimmungskoeffizienten über 80% können als recht gut angesehen werden (der Korrelationskoeffizient übersteigt 90%). Die Gleichheit des Bestimmungskoeffizienten mit der Einheit bedeutet, dass die erläuterte Variable vom betrachteten Modell genau beschrieben wird “ (ebenda).
Um das Vorhersageproblem zu lösen, verwenden wir die folgenden Algorithmen:
Lineare Algorithmen:
-
Lineare Regression ('LR')
- Gratregression (Gratregression) /
Gratregression ('R')
- Lasso-Regression (aus dem englischen LASSO - Least Absolute Shrinkage and Selection Operator) /
Lasso-Regression ('L')
- ELN-
Regressionsmethode (
Elastic Net Regression )
- LARS-Methode (
Least Angle Regression )
- Bayesian Ridge Regression /
Bayesian Ridge Regression ('BR')
Nichtlineare Algorithmen:
-
k-Nearest-Neighbour-Regressor-Methode (KNR-
Methode)-
Decision Tree Regressor ('DTR')
-
Lineare Unterstützungsvektormaschine (Regression) /
Lineare Unterstützungsvektormaschine - Regression / ('LSVR')
-
Support-Vektor- Methode (Regression) /
Epsilon-Support-Vektor-Regression ('SVR')
Ensemble-Algorithmen:
- AdaBoost (Regression) /
AdaBoost Regressor ('ABR') (AdaBoost = Adaptive Boosting)
- Bagging (Regression) /
Bagging Regressor ('BR') (Bagging = Bootstrap Aggregation)
-
Extra Trees Regressor ('ETR')
- Gradient Boosting (Regression) /
Gradient Boosting Regressor ('GBR')
-
Zufällige Waldklassifizierung (Regression) /
Zufälliger Waldklassifizierer ('RFR')
Daher enthält die Liste der "Modelle" die folgenden Modelle:
models = [] models.append(('LR', LinearRegression())) models.append(('R', Ridge())) models.append(('L', Lasso())) models.append(('ELN', ElasticNet())) models.append(('LARS', Lars())) models.append(('BR', BayesianRidge(n_iter=n_iter))) models.append(('KNR', KNeighborsRegressor())) models.append(('DTR', DecisionTreeRegressor())) models.append(('LSVR', LinearSVR())) models.append(('SVR', SVR())) models.append(('ABR', AdaBoostRegressor(n_estimators=n_estimators))) models.append(('BR', BaggingRegressor(n_estimators=n_estimators))) models.append(('ETR', ExtraTreesRegressor(n_estimators=n_estimators))) models.append(('GBR', GradientBoostingRegressor(n_estimators=n_estimators))) models.append(('RFR', RandomForestRegressor(n_estimators=n_estimators)))
Wie bei der Klassifizierung erfolgt die Bewertung der Wirksamkeit jedes Algorithmus durch Kreuzvalidierung. Die angezeigte Meldung enthält die folgenden Informationen: Der Name des Modells in Form einer Abkürzung, die durchschnittliche Punktzahl einer 10-fachen Kreuzvalidierung für Trainingsdaten (Metrik 'r2'), die Standardabweichung und der Bestimmungskoeffizient r2 für die Testdaten sind in Klammern angegeben.
Nach dem Ausführen des Codes erhalten wir die folgenden Ergebnisse:
LR: train = 0.746 (0.068) / test = 0.579 R: train = 0.744 (0.067) / test = 0.570 L: train = 0.689 (0.070) / test = 0.641 ELN: train = 0.677 (0.074) / test = 0.662 LARS: train = 0.744 (0.069) / test = 0.579 BR: train = 0.739 (0.069) / test = 0.571 KNR: train = 0.434 (0.288) / test = 0.538 DTR: train = 0.671 (0.145) / test = 0.637 LSVR: train = 0.550 (0.144) / test = 0.459 SVR: train = -0.012 (0.048) / test = -0.003 ABR: train = 0.810 (0.078) / test = 0.763 BR: train = 0.854 (0.064) / test = 0.805 ETR: train = 0.889 (0.047) / test = 0.836 GBR: train = 0.878 (0.042) / test = 0.863 RFR: train = 0.852 (0.068) / test = 0.819
Spannendiagramm:
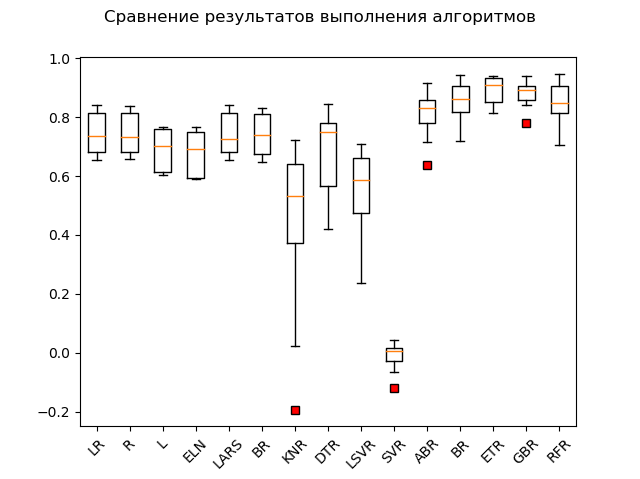
Die offensichtlichen Anführer sind die Ensemble-Methoden 'GBR' (Gradient Boosting), 'ETR' (Extra-Bäume), 'RFR' (Random Forest) und 'BR' (Bagging):
GBR: train = 0.878 (0.042) / test = 0.863 ETR: train = 0.889 (0.047) / test = 0.836 RFR: train = 0.852 (0.068) / test = 0.819 BR: train = 0.854 (0.064) / test = 0.805 ABR: train = 0.810 (0.078) / test = 0.763 ELN: train = 0.677 (0.074) / test = 0.662 L: train = 0.689 (0.070) / test = 0.641 DTR: train = 0.671 (0.145) / test = 0.637 LR: train = 0.746 (0.068) / test = 0.579 LARS: train = 0.744 (0.069) / test = 0.579 BR: train = 0.739 (0.069) / test = 0.571 R: train = 0.744 (0.067) / test = 0.570 KNR: train = 0.434 (0.288) / test = 0.538 LSVR: train = 0.550 (0.144) / test = 0.459 SVR: train = -0.012 (0.048) / test = -0.003
Eine Art "Adabust", "Loshara" hinkt hinterher.
Vielleicht kämpfen die drei Führer gegen Standardisierung und Normalisierung. Lassen Sie uns herausfinden, indem Sie den Rest des Codes ausführen.
Die Ergebnisse sind wie folgt:
SS_LR: train = 0.746 (0.068) / test = 0.579 SS_R: train = 0.746 (0.068) / test = 0.578 SS_L: train = 0.678 (0.054) / test = 0.510 SS_ELN: train = 0.665 (0.060) / test = 0.513 SS_LARS: train = 0.744 (0.069) / test = 0.579 SS_BR: train = 0.746 (0.066) / test = 0.576 SS_KNR: train = 0.763 (0.098) / test = 0.739 SS_DTR: train = 0.610 (0.242) / test = 0.629 SS_LSVR: train = 0.727 (0.091) / test = 0.482 SS_SVR: train = 0.653 (0.126) / test = 0.610 SS_ABR: train = 0.811 (0.076) / test = 0.819 SS_BR: train = 0.853 (0.074) / test = 0.813 SS_ETR: train = 0.887 (0.048) / test = 0.846 SS_GBR: train = 0.878 (0.038) / test = 0.860 SS_RFR: train = 0.851 (0.071) / test = 0.818 N_LR: train = 0.751 (0.099) / test = 0.576 N_R: train = 0.287 (0.126) / test = 0.271 N_L: train = -0.030 (0.032) / test = -0.000 N_ELN: train = -0.007 (0.030) / test = 0.023 N_LARS: train = 0.751 (0.099) / test = 0.576 N_BR: train = 0.744 (0.100) / test = 0.589 N_KNR: train = 0.485 (0.192) / test = 0.504 N_DTR: train = 0.729 (0.080) / test = 0.765 N_LSVR: train = 0.182 (0.108) / test = 0.136 N_SVR: train = 0.086 (0.076) / test = 0.084 N_ABR: train = 0.795 (0.053) / test = 0.752 N_BR: train = 0.854 (0.054) / test = 0.827 N_ETR: train = 0.877 (0.048) / test = 0.850 N_GBR: train = 0.852 (0.063) / test = 0.872 N_RFR: train = 0.852 (0.051) / test = 0.801
Wie Sie sehen, haben Ensemblemethoden immer noch die Nase vorn.'Top 5' enthält die folgenden Ergebnisse: N_GBR: train = 0.852 (0.063) / test = 0.872 GBR: train = 0.878 (0.042) / test = 0.863 SS_GBR: train = 0.878 (0.038) / test = 0.860 N_ETR: train = 0.877 (0.048) / test = 0.850 SS_ETR: train = 0.887 (0.048) / test = 0.846
:
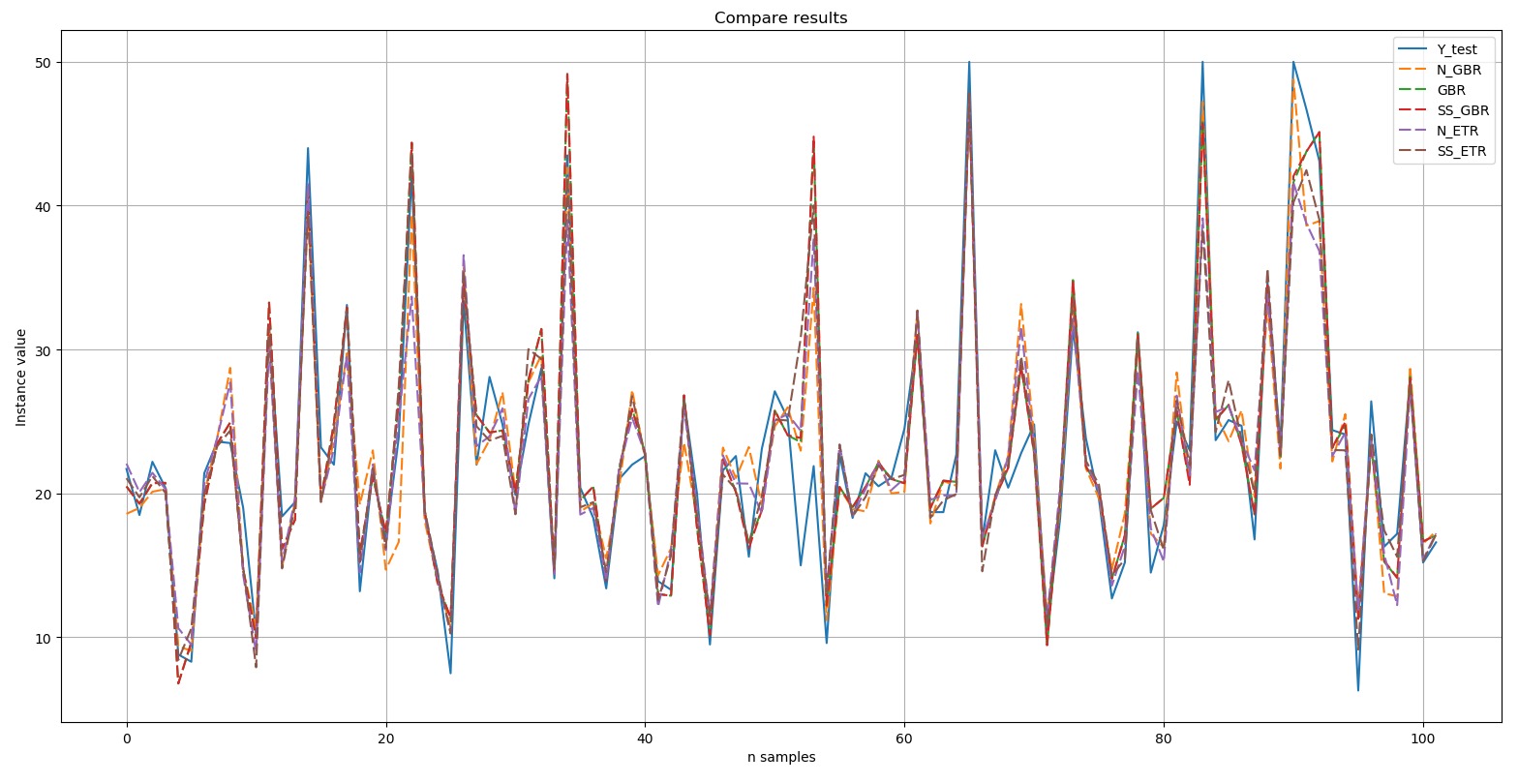Y-test – . , , (dashed). , , .
, Top 5:
, - 'boston house-price' «» ('GBR') - ('ETR'). .
Nachwort
- (). , 'digits', 10 , 'boston house-price', «» «» .
, , GitHub. :
.
— -. , : . :)
. , , , . , «- », , , , ( ):), ; , ; , «». :)
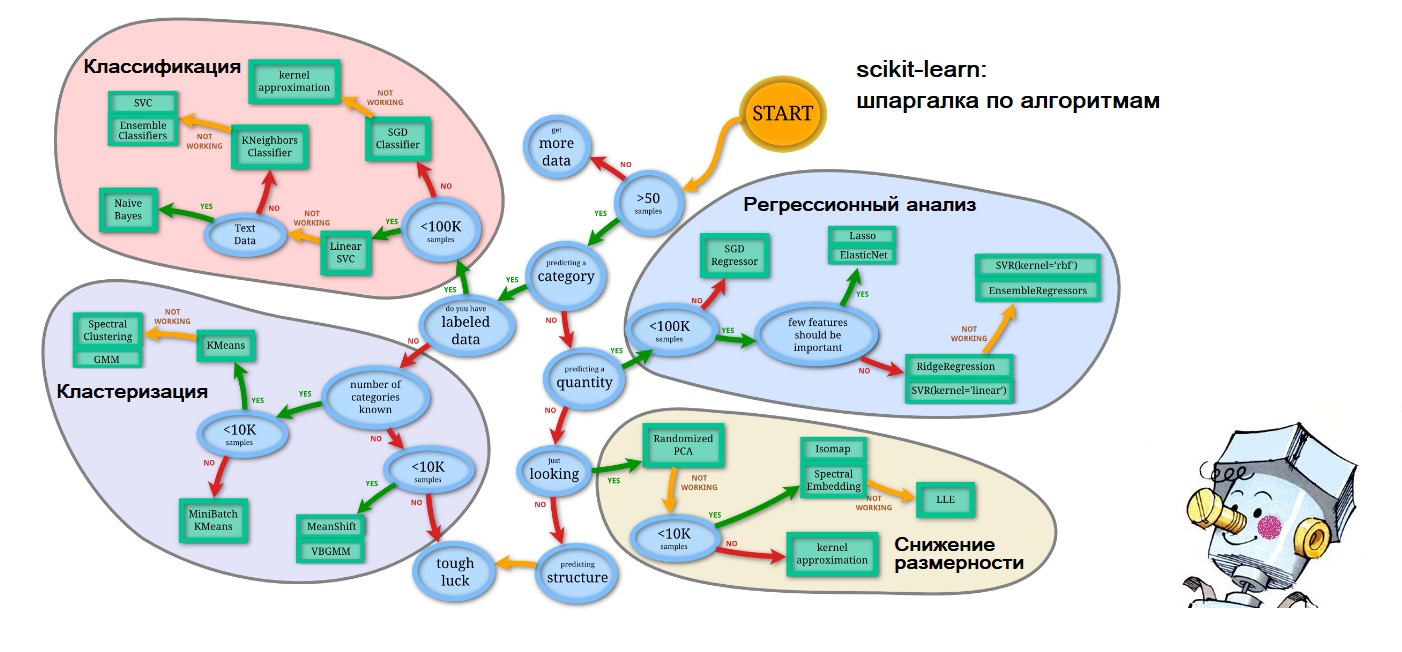
PS , , - : scikit-learn.org (
'Choosing the right estimator' ):
. – .